第七章 平面体的截交线.

§4-2 平面与平面立体表面相交平面与立体表面的交线，称为截交线；当平面切割立体时，由截交线围成的平面图形，称为截面。

一、平面立体的截交线和断面如图4-16a所示，平面立体的截交线是截平面上的一个多边形，它的顶点是平面立体的棱线或底边与截平面的交点，它的边是截平面与平面立体表面的交线，图中截平面P与三棱锥的截交线是一个三角形ⅠⅡⅢ。

如图4-16b中的黑色图形所示，已知三棱锥SABC和正垂的截平面P，求作截交线的三面投影。

作图过程如图4-16b中的红色图形所示：（1）在棱线SA、SB、SC的正面投影s＇a＇、s＇b＇、s＇c＇与截平面P的有积聚性的迹线P v的相交处，作出它们的交点Ⅰ、Ⅱ、Ⅲ的正面投影1＇、2＇、3＇，与P v相重合的直线1＇2＇3＇，即为截交线△ⅠⅡⅢ的正面投影。

（2）由1＇、2＇、3＇引投影连线，分别与sa、sb、sc和s″a″、s″b″、s″c″交出1、2、3和1″、2″、3″。

连接这些点的同面投影，就作出了截交线△ⅠⅡⅢ的水平投影△123和侧面投影△1″2″3″。

由于三个棱面的水平投影和棱面SAB、SCA的侧面投影都可见，在其上的截交线的同面投影12、23、31和1″2″、3″1″也都可见，画粗实线；棱面SBC的侧面投影不可见，在其上的截交线的侧面投影2″3″也不可见，画细虚线。

如图4-17a中的黑色图形所示，已知五棱柱的正面投影和水平投影，并用正垂面P切割掉左上方的一块，被切割掉的部分用细双点划线表示，求作截交线以及五棱柱被切割后的三面投影。

因为截交线的各边是正垂面P与五棱柱的棱面和顶面的交线，它们的正面投影都重合在P v上，因为截交线的正面投影已知，五棱柱被切割后的正面投影也已知，只要作出截交线的水平投影，就可以作出五棱柱被切割后的水平投影。

根据五棱柱的正面投影和水平投影，可以作出它的侧面投影；同理，由已作出的截交线的正面投影和水平投影，也可以作出截交线的侧面投影，从而作出五棱柱被切割后的侧面投影。

简述平面体截交线的特点及基本作图方法平面体截交线作图是解决设计和制造问题中必不可少的一种方法。

它可以使用交叉视图，把截面线根据实际需要以体积的形式显示出来，从而节省时间和精力。

因此，对平面体截交线的作图了解很重要。

平面体截交线的特点主要有三个：一是每条截面线由四边形组成；二是四边形的两条对角线是直线；三是截面面的两个角是直角。

这些特点使得在作图过程中，需要根据所给的尺寸和角度，以及其他信息，绘制出截面线。

作图时，首先，要确定图形中心点位置，并绘制出坐标系统；其次，要确定截面线所在位置，并在坐标系统中绘制出正确的角度和尺寸；最后，需要绘制截面线，以及其他信息所需的虚线等。

绘制完成以后，还要对图形中的每个细节进行检查，确保坐标系统的准确性，并确保图形的尺寸和角度正确无误。

因此，从以上可以看出，平面体截交线作图并不容易，但是熟练掌握了一定的绘图技巧和技能之后，就可以轻松完成作图。

首先，要把握好坐标系统，这样才能绘制出正确的角度和尺寸；其次，要学会细分图形，从而更准确地绘制出截面线，并对图形中的每个细节进行检查；最后，要灵活运用多种绘图技巧，如拉直、估算、填充等，以绘制出更加准确的图形。

另外，在绘制截面线的过程中，也可以使用计算机辅助设计软件来提高绘图效率，这样可以有效地完成绘图任务。

总之，平面体截交线作图不仅需要对绘图技巧有一定的把握，而且也需要一定的经验，只有熟练掌握了相关技能，才能够更好地完成绘图任务。

简述平面体截交线的特点及基本作图方法平面体截交线是我们在绘制立体几何图形时所使用的一种绘制方法，它的特点是能够将所有三维图形折叠到二维平面，从而进行更清晰的比较和分析。

平面体截交线是一种十分高效灵活的绘制方法，可以为立体几何图形的折叠和建模提供便利。

本文将简要介绍平面体截交线的特点及基本作图方法。

首先，我们来看一下平面体截交线的特点。

平面体截交线可以把三维图形折叠到二维平面，而且是通过绘制三维图形投影后的二维图形来实现的。

平面体截交线可以将复杂的三维图形折叠成一个个小块，使得我们可以更清晰地比较图形的各个部分，从而更方便地对立体几何图形进行分析和研究。

在使用平面体截交线进行几何图形绘制时，我们可以更容易地判断平面体之间的位置关系，从而更有效地把握几何图形的结构。

其次，我们来看一下平面体截交线基本作图方法。

首先，我们需要采用平法绘制三维图形的投影，即平行投影法。

平行投影法可以将所有三维图形折叠到同一平面上，使得我们可以更清晰地比较三维图形各个部分之间的位置关系，从而更加便捷的绘制平面体截交线。

其次，我们需要采用透视投影法来进行图形的折叠。

透视投影法可以将所有三维图形折叠到一个个小块，使得我们可以更清晰地比较图形的各个部分，从而更加便捷的绘制平面体截交线。

最后，我们需要使用点线投影法来实现平面体截交线的绘制，即把几何体上的点和线投影到一个平面，从而得到平面体截交线的形状。

以上就是关于平面体截交线的特点及基本作图方法的简要介绍，它主要的特点是将三维图形折叠到二维平面，可以为立体几何图形的折叠和建模提供便利，并且能够更清晰地比较图形的各个部分。

在绘制平面体截交线时，采用平行投影法、透视投影法和点线投影法可以大大提高绘图效率，使得我们可以更容易地判断平面体之间的位置关系，从而更有效地把握几何图形的结构。

第七章截交线和相贯线§7-1概述形体与形体连接都有相交线。

介绍几个基本概念一个桔子、用刀切开1．形体：桔子；2．截平面：刀——用于截开形体的平面；3．截交线：桔子表面与刀相交的线——形体与截平面相接的表面线；4．断面：桔子内部——截交线所包含的形体内部；注：①截平面是一个求截交线的方式；②求截交线是为了解决后面的相贯线的有效方式。

5．贯穿点：是直线与形体的相交点；6．相贯线：是两形体表面相交线。

贯穿点、相贯线都有一个特点———共有性，即属于形体也属于另一直线或形体。

§7-2截交线一、平面体的截交线平面体的特征就是形体与平面组成。

两平面相交，交线一定是直线。

（一）平面体截交线的特点：1、由多段折线组成；2、转折点在棱线上；3、截交线是封闭性。

（二）形体被多个截平面所截：1、截交线成多个平台；2、每个平面有一相互相交的交线；3、转折点在棱线上和截平面相交处。

（三）求截交线方法：1、棱线法——这是由平面体特征所决定的。

2、表面（取点）辅助线法——这是多个截平面相交不一定在棱线上。

Ⅰ、Ⅱ、Ⅲ点在SA、SB、SC棱线上。

例：求四棱面的2投影例：穿孔二、曲面体的截交线曲面体的截交线是平面曲线。

曲面体与截平面相互位置不同，截交线不同。

（一）典型的截交线1、P187 表7-1，圆柱上的截交线——椭圆、圆、矩形2、P189 表7-2，圆锥上的截交线——椭圆ω＞θ抛物线ω=θ，双曲线ω=0，园ω=90°两条素线ω＜θω为截平面与圆锥轴线夹角，θ为圆锥半角。

（二）求截交线的方法：1、素线法：适用圆柱体、圆锥体。

2、纬园法：适用圆锥体、球体等。

3、辅助平面法（换面法）：适用轴线与投影面不垂直情况。

（三）求截交线的步骤1、先求特殊点；2、再求一般点；3、连点成线；4、判别可见性。

例：求圆柱体开槽层的投影例：求圆柱体的水平投影例：求圆锥体的截交线例：求球体表面线例：求园环体截交线贯穿点复述或提问：截交线概念。

第七章截交线和相贯线§7-1概述
§7-2截交线
§7-3相贯线
§7-1概述
在组合形体和建筑形体的表面上，经常出现一些交线。

这些交线有些是形体被平面截割而产生，有些则是两形体相交而形成。

如图所示的沈阳夏宫，主体是球顶建筑，其四周有锥壳屋面与其相交。

锥壳屋面的檐口曲线Ⅰ 就是平面与锥面的交线，锥壳屋面与中央主体球顶屋面相交处的空间曲线Ⅱ 则是锥面与球面的交线。

截交线
基本形体被一个或多个平面截割（例如图a所示的四棱锥被一个平面截割，图b所示的圆柱被两个平面截割），必然在形体的表面上产生交线。

假想用来截割形体的平面称为截平面。

截平面与形体表面的交线称为截交线。

截交线围成的平面图形称为断面。

相贯线
有些建筑形体是由两个相交的基本形体组成的，这种形体称为相贯体，相贯体的表面交线称为相贯线。

两形体相贯，可以是平面体与平面体相贯（图a），平面体与曲面体相贯（图b）以及曲面体与曲面体相贯（图）。

§7-2 截交线一、平面体的截交线
二、曲面体的截交线
1. 圆柱的截交线
2. 圆锥的截交线
3. 球的截交线
4. 组合形体的截交线
§7-3 相贯线
外表面和外表面相贯外表面和内表面相贯
内表面和内表面相贯
平面体和平面体相贯平面体和曲面体相贯
曲面体和曲面体相贯。

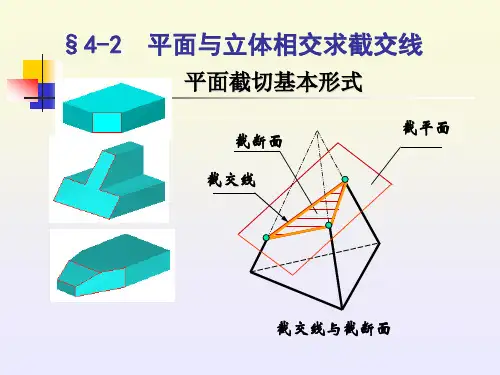
平面体的截交线假想用来截割形体的平面，称为截平面，截平面与形体表面的交线称为截交线，截交线围成的平面图形称为断面，如图，R为截平面，DEF为截交线，平面DEF为断面。

截交线的基本性质：1.截交线既然是截平面与立体表面的交线，那么它必然是属于截平面和立体表面的共有线。

截交线上所有的点也必然是立体表面和截平面上的共有点；2.由于立体的表面都是封闭的，因此截交线也必定是一个或若干个封闭的平面折线，折点在形体的棱边上，求截交线实质是求棱边与截平面的交点；从左图中可知,平面R与三棱锥相交后，其截交线是一个三角形。

其中，围成截交线的每一直线段，都是三棱锥的棱面与截平面R的交线；截交线上的每一个顶点（折点），都是三棱锥的棱线与截平面R的交点。

由此，我们可以归纳出求平面立体截交线的两种方法：1.交点法首先求出平面立体上参与相交的各棱线（或底边）与截平面的交点，然后将位于同一棱面上（或同一底面上）的两点依次相连，即得截交线。

2.交线法分别作出平面立体上参与相交的各棱面（或底面）与截平面的交线，各段交线所连成的多边形即截交线。

在解题过程中，究竟采用哪一种作图方法求截交线，则应根据所给题目的条件以及能否使作图简化而进行选择。

在连线时还应判别交线各段投影的可见性，将可见的与不可见的各段分别用实线和虚线表示清楚。

例1.求正垂面 P 与三棱锥的截交线。

分析：从正面投影中可清楚地看到，截平面P与三棱锥的底面不相交，只与三个棱面相交。

因此，截交线是一个三角形。

由于截平面是一正垂面，它的正面投影有积聚性，因此，截交线的正面投影必重影于Pv上，且Pv 与三棱锥正面投影重叠的一段。

三条棱线SA、SB、SC与截平面交点的正面投影必然落在这三条棱线的正面投影（s'a'、s'b'、s'c'）与Pv 的交点处，即 1'、2'、3' 。

这样，截交线的正面投影就无需作图了。