阻尼振动和受迫振动

机械振动中的阻尼振动与受迫振动在机械系统中，振动是一种普遍存在的现象，它包含着阻尼振动和受迫振动两种类型。

阻尼振动是指系统在一定的阻尼作用下运动的周期性减弱振动，而受迫振动是指系统受到外部力的作用而发生周期性振动。

本文将探讨机械振动中的阻尼振动和受迫振动的特点及其应用。

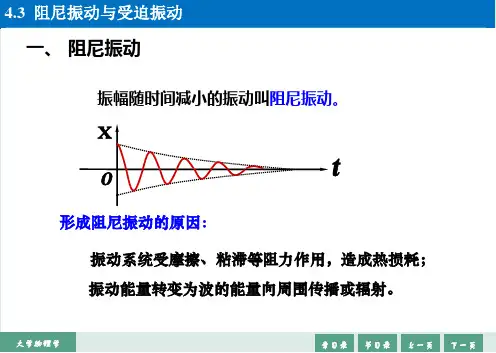
一、阻尼振动阻尼振动是指振动系统在受到阻力的作用下产生的振动。

阻尼力可以分为粘性阻尼、干摩擦阻尼和液体摩擦阻尼等不同形式。

阻尼振动的特点是振幅逐渐减小，振动频率也逐渐减小。

阻尼振动的主要原因是能量的损失。

当机械系统受到阻尼力的作用时，振动系统的机械能会逐渐转化为热能而损失。

这导致振动幅度逐渐减小，最终停止振动。

例如，摆钟在受到空气阻力的影响下，其摆动幅度会逐渐减小，最终停止。

阻尼振动的应用广泛。

在机械工程中，阻尼振动常常被用于减震和能量吸收的装置设计。

例如，在车辆的悬挂系统中使用减震器，可以有效地缓解车辆行驶中的颠簸感。

同时，阻尼振动还常用于物体的减振和抗震设计，例如建筑物中的隔震装置。

二、受迫振动受迫振动是指振动系统在外部力的作用下产生的振动。

外力可以是周期性的，也可以是非周期性的。

受迫振动的特点是振幅和频率与外力的频率相关。

外力对振动系统的影响可以分为共振和强迫两种情况。

共振是指外力的频率接近或等于振动系统的固有频率时，振动幅度会显著增大。

强迫是指外力的频率与振动系统的固有频率有一定的差别，但仍然能引起系统振动。

受迫振动在实际生活中有许多应用。

例如，在音乐中，乐器的共振现象使得乐器能够产生特定的音调。

另外，受迫振动还在工程领域中有着广泛的应用，如振动筛、振动输送机等。

它们利用外力作用产生振动，以完成特定的分选和输送任务。

三、阻尼振动与受迫振动的关系阻尼振动与受迫振动是机械振动中两种常见的振动类型，它们在某些情况下可以相互转化。

当受迫振动系统存在阻尼时，会产生阻尼振动。

此时，外力的频率与振动系统的固有频率相同或接近时，阻尼振动的幅度会受到外力的影响，产生共振效应。

高中物理波动与振动中的阻尼振动与受迫振动在高中物理的学习中，波动与振动是一个重要的板块，其中阻尼振动和受迫振动是两个关键的概念。

理解这两种振动形式，对于我们深入掌握物理世界的规律有着重要的意义。

首先，让我们来认识一下阻尼振动。

阻尼振动，简单来说，就是在振动过程中，由于受到阻力的作用，振动的能量逐渐减少，振动的幅度也随之逐渐减小，最终振动停止。

想象一下，一个荡秋千的小孩，如果没有外力的持续推动，也没有任何的阻力，那么秋千会一直以相同的幅度摆动下去，这就是理想的无阻尼振动。

但在现实中，空气的阻力总是存在的。

随着秋千的摆动，空气阻力会不断消耗秋千的能量，使得秋千摆动的幅度越来越小，直到最终停下来，这就是阻尼振动的一个常见例子。

阻尼振动的一个显著特点就是振幅的衰减。

比如说，一个弹簧振子在光滑的水平面上振动，如果没有摩擦力等阻力，它会一直做等幅振动。

但如果在粗糙的平面上振动，摩擦力就会不断消耗振子的能量，振幅也就会越来越小。

阻尼振动的表达式通常比较复杂，但我们可以通过一些简化的模型来理解其基本规律。

在阻尼较小的情况下，振动的频率变化不大，但振幅会按照一定的规律逐渐减小。

接下来，我们再来看受迫振动。

受迫振动是指物体在周期性外力作用下的振动。

这个外力就像是一个“强迫者”，迫使物体按照外力的频率振动。

比如说，家里的洗衣机在脱水时，电机的转动会带动洗衣机内胆振动，这个振动就是受迫振动。

电机的转动频率决定了内胆振动的频率。

受迫振动有一个很重要的特点，那就是当外力的频率等于物体的固有频率时，物体的振幅会达到最大，这种现象被称为共振。

共振现象在生活中既有好处也有坏处。

比如，在建筑设计中，如果建筑物的固有频率与地震波的频率接近，就可能在地震中发生严重的破坏，这是共振的坏处。

而在一些乐器的设计中，利用共振可以让乐器发出更响亮、更美妙的声音，这就是共振的好处。

从能量的角度来看，阻尼振动是能量不断减少的过程，而受迫振动是外界不断输入能量的过程。

阻尼振动和受迫振动的动力学振动是物体在围绕平衡位置上下运动的一种现象。

当物体受到外力的作用时，它可能出现阻尼振动或受迫振动。

本文将分别讨论这两种振动的动力学特征。

1. 阻尼振动阻尼振动指的是物体在受到阻尼力的影响下进行振动。

阻尼力是由于摩擦或阻力而产生的一种力。

一般而言，阻尼力与物体的运动速度成正比。

在阻尼振动中，振幅会逐渐减小，直到最终趋于零。

这是因为阻尼力的作用导致了振动能量的损失。

阻尼振动的动力学方程可以表示为：m * d^2x/dt^2 + c * dx/dt + k * x = 0其中，m为物体的质量，x为物体的位移，t为时间，c为阻尼系数，k为弹簧的劲度系数。

这是一个二阶常微分方程，可以通过求解得出振动的解析解。

2. 受迫振动受迫振动是指物体在受到外力周期性作用下进行振动。

外力的周期性作用可能是恒定的或变化的。

受迫振动的一个典型例子是在谐振子中。

谐振子是一个具有弹簧和质量的系统，当受到周期性驱动力时，谐振子会在特定的驱动频率下展现出共振现象。

共振是指外力频率与谐振子固有频率相同或接近时的现象。

受迫振动的动力学方程可以表示为：m * d^2x/dt^2 + c * dx/d t + k * x = F0 * sin(ω * t)其中，F0为驱动力的振幅，ω为驱动力的角频率。

通过求解这个方程，可以得到受迫振动的解，包括相位和幅频特征。

3. 动力学特征比较阻尼振动和受迫振动在动力学特征上有一些区别。

首先，阻尼振动的振幅会随时间逐渐减小，直到最终停止。

而受迫振动在存在共振现象时，振幅可能会增大甚至无限增大。

其次，阻尼振动的频率与振幅无关，而受迫振动的频率会对振幅产生明显的影响。

当驱动力的频率接近谐振子的固有频率时，振幅会显著增加。

最后，阻尼振动和受迫振动在相位上也略有不同。

在阻尼振动中，振动的相位随着时间的推移而发生改变。

而在受迫振动中，振动的相位与驱动力的相位存在一定的差距。

综上所述，阻尼振动和受迫振动都是振动的一种形式，但它们在动力学特征上有一些差别。

阻尼振动与受迫振动●阻尼振动●受迫振动●共振1．阻尼振动实例a. 阻尼弹簧振子，阻力γγ其中。

实例b. RLC谐振电路或写作其中。

分析：引入阻尼将引起能量的减小，计算能量改变率，β（等于阻尼做功的功率）。

如果很小，基本上还是简谐振动，但由于能量消耗，振幅会逐渐减小，解的形式近似为：能量，β一个周期内能量的消耗率：其中称为品质因数(quality factor)，简称值(Q factor)。

从数量级上讲，Q值就是把储存的能量衰减完，振子中能够振荡的次数。

（注：RLC谐振电路，）精确解：(a)弱阻尼()其中。

与近似分析的结果相比，只是频率有所减小。

(b)过阻尼()其中。

无振荡，呈指数衰减。

注意是的减函数，衰减速度随增大反而减慢。

(c)临界阻尼()，无振荡，但衰减最快。

2．受迫振动实例a. 驱动弹簧振子γ实例b. RLC串联电路非齐次线性方程解的一般形式：其中是原方程的一个解（称为特解），是齐次方程的任意解。

写成复数形式，令满足方程则满足方程令，其中所以可取称为稳态解，而把称为暂态解。

3．共振为简单起见，只讨论速度共振。

的振幅为性质：(1)驱动频率与固有频率相等（）时，时速度振幅（或平均动能）最大，出现共振。

(2)共振时，速度与驱动力同相位，驱动一直做正功。

(3)驱动频率与固有频率相差越大，振幅（动能）越小，形成一个共振峰。

(4)Q值越大，共振峰越高，同时也越窄（对驱动频率的选择性越高）。

共振的应用：乐器、无线电接收、调Q激光、核磁共振与电子自旋共振等。

共振有时会造成破坏，需要避免。

阻尼振动与受迫振动振动是自然界中普遍存在的一种现象，它在物理学、工程学等领域中具有重要的应用价值。

而阻尼振动和受迫振动是振动学中两个重要的概念。

阻尼振动是指在振动系统中存在摩擦或阻力的情况下所产生的振动。

当一个物体受到外力作用而开始振动时，若存在阻尼，振动的幅度将逐渐减小，最终停止。

这种振动方式在日常生活中很常见，例如钟摆摆动时逐渐停下来的过程。

阻尼振动的特点是振幅逐渐减小，振动频率不变。

这是因为阻尼力与振动速度成正比，而速度越大，阻尼力就越大。

因此，振动系统在受到外力作用后，振幅将逐渐减小，直到最终停止振动。

与阻尼振动相对应的是受迫振动，它是指在外力作用下振动系统发生的振动。

受迫振动的特点是振幅随时间的变化而发生周期性的变化，振幅的变化与外力的频率和振幅有关。

受迫振动的一个重要应用是共振现象。

当外力的频率与振动系统的固有频率相等时，共振现象会发生。

在共振状态下，振幅将达到最大值，这是因为外力与系统的振动频率相同，能够为系统提供持续的能量输入，从而使振幅增大。

阻尼振动和受迫振动经常在实际工程中应用。

例如，在汽车悬挂系统中，为了提高乘坐舒适性，往往会采用阻尼装置来减小车身的振动。

而在建筑工程中，为了避免共振现象对建筑物产生破坏性影响，工程师们会根据建筑物的固有频率来设计结构。

除了工程领域，阻尼振动和受迫振动也在物理学和生物学中有广泛的应用。

例如，在电子学中，阻尼振动可以用于减小电路的振荡幅度；在生物学中，研究细胞的振动特性有助于了解细胞的结构和功能。

总之，阻尼振动和受迫振动是振动学中的两个重要概念。

阻尼振动是指在存在阻力或摩擦力的情况下发生的振动，振幅逐渐减小；而受迫振动是指在外力作用下发生的振动，振幅随时间的变化而发生周期性变化。

这两种振动方式在实际应用中具有重要意义，对于理解和应用振动学理论有着重要的作用。

《阻尼振动与受迫振动》实验报告工程物理系核41 崔迎欢 2014011787一．实验名称：阻尼振动与受迫振动二．实验目的1．观测阻尼振动，学习测量振动系统基本参数的方法；2．研究受迫振动的幅频特性和相频特性，观察共振现象；3．观测不同阻尼对受迫振动的影响。

三．.实验原理1．有粘滞阻尼的阻尼振动弹簧和摆轮组成一振动系统，设摆轮转动惯量为J，粘滞阻尼的阻尼力矩大小定义为角速度dθ/dt与阻尼力矩系数γ的乘积，弹簧劲度系数为k，弹簧的反抗力矩为-kθ。

忽略弹簧的等效转动惯量，可得转角θ的运动方程为记ω0为无阻尼时自由振动的固有角频率，其值为ω0=，定义阻尼系数β=γ/（2J），则上式可以化为：小阻尼即时，阻尼振动运动方程的解为（*）由上式可知，阻尼振动角频率为，阻尼振动周期为2．周期外力矩作用下受迫振动的解在周期外力矩Mcosωt激励下的运动方程和方程的通解分别为这可以看作是状态（*）式的阻尼振动和频率同激励源频率的简谐振动的叠加。

一般t>>τ后，就有稳态解稳态解的振幅和相位差分别为其中，φ的取值范围为（0，π），反映摆轮振动总是滞后于激励源支座的振动。

3．电机运动时的受迫振动运动方程和解弹簧支座的偏转角的一阶近似式可以写成式中αm是摇杆摆幅。

由于弹簧的支座在运动，运动支座是激励源。

弹簧总转角为。

于是在固定坐标系中摆轮转角θ的运动方程为也可以写成于是得到由θm的极大值条件可知，当外激励角频率时，系统发生共振，θm有极大值。

引入参数，称为阻尼比。

于是，我们得到四．实验仪器：波耳振动仪五．实验步骤。

1．打开电源开关，关断电机和闪光灯开关，阻尼开关置于“0”档，光电门H、I可以手动微调，避免和摆轮或者相位差盘接触。

手动调整电机偏心轮使有机玻璃转盘F上的0位标志线指示0度，亦即通过连杆E和摇杆M使摆轮处于平衡位置。

染货拨动摆轮使偏离平衡位置150至200度，松开手后，检查摆轮的自由摆动情况。

正常情况下，振动衰减应该很慢。