电路分析等效变换
- 格式:ppt
- 大小:4.75 MB
- 文档页数:19

等效变换和替代定理等效变换是指在不改变电路特性的情况下,通过改变电路中元件的参数或者改变元件的位置,使得电路的形式发生变化,但是电路的特性不变。
等效变换是电路分析中常用的一种方法,可以简化电路分析的过程,提高电路分析的效率。
替代定理是指在电路中,任何两个电阻或电源可以互相替代,只要它们的电压和电流关系相同。
替代定理是电路分析中常用的一种方法,可以简化电路分析的过程,提高电路分析的效率。
下面分别对等效变换和替代定理进行详细介绍:一、等效变换1. 电阻的串并联变换在电路中,若有多个电阻串联或并联,可以通过串并联变换将它们简化为一个等效电阻。
串并联变换的原理是根据欧姆定律和基尔霍夫定律,将多个电阻串联或并联的电路转化为一个等效电阻的电路。
2. 电压源和电流源的等效变换在电路中,若有多个电压源或电流源,可以通过等效变换将它们简化为一个等效电源。
电压源和电流源的等效变换的原理是根据基尔霍夫定律和欧姆定律,将多个电压源或电流源的电路转化为一个等效电源的电路。
3. 电阻的星三角变换在电路中,若有多个电阻星型连接或三角形连接,可以通过星三角变换将它们简化为一个等效电阻。
星三角变换的原理是根据欧姆定律和基尔霍夫定律,将多个电阻星型连接或三角形连接的电路转化为一个等效电阻的电路。
二、替代定理1. 电阻的替代定理在电路中,任何两个电阻可以互相替代,只要它们的电压和电流关系相同。
电阻的替代定理可以简化电路分析的过程,提高电路分析的效率。
2. 电源的替代定理在电路中,任何两个电源可以互相替代,只要它们的电压和电流关系相同。
电源的替代定理可以简化电路分析的过程,提高电路分析的效率。
总之,等效变换和替代定理是电路分析中常用的两种方法,它们可以简化电路分析的过程,提高电路分析的效率。
在实际应用中,需要根据具体情况选择合适的方法进行电路分析。



电路分析中的等效变换王 辰 5050309165 蔡浩宇 5050309164在电路的分析过程中,有时会因为电路的复杂变得无法下手。
如果利用电路的某些特点,将电路的形式进行某种变换,就可以达到简化电路、减少求解方程数的目的,从而大大简化求解。
这些变换一般都是基于等效电路的原理进行的。
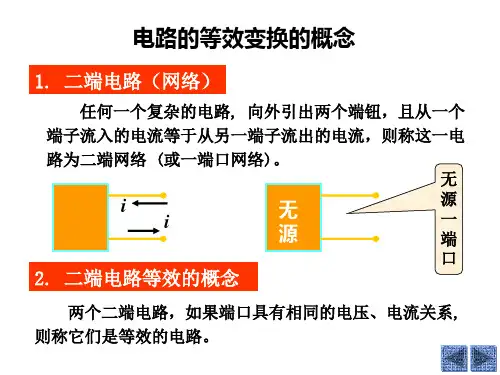
对了电路网络来说,如果端钮一一对应的端口电路和具有相同的端口特性,即相同的两组端口电压分别代入两个电路的端口特性方程会得出相同的两组端口电流,或者将相同的两组端口电流代入两个电路的端口特性方程会得出相同的两组端口电压,则二者相互等效,两个电路就互为等效电路。
n 1N 2N 一、线性电阻电路的等效分析线性电阻电路的常见的几种等效变换包括电阻串联与并联的等效变换、电源的等效变换、含受控源的电路的等效变换、Y形电路和Δ形电路的等效变换、戴维南等效以及诺顿等效等。
1、基本电阻元件的串联、并联和混联,电源的串、并联分析此类电路的等效变换较为简单,依据电路器件的特性可以较为方便的求出电路的包括等效电阻在内的各种参数。
在此就不再加以详细说明。
2、Y/Δ、Δ/Y等效变换Y/Δ及Δ/Y等效变换是三端钮网络的等效变换,它可以将Y连接的三端钮网络等效变化成Δ连接,也可以将Δ连接的三端钮网络等效变化成Y连接。
Y连接和Δ连接如图1所示。
电压、和分别相等,即、、12u 23u 31u 11b a i i =22b a i i =33b a i i =它们彼此等效。
利用KCL 和KVL 可求得等效变化公式: Y⇒Δ等效变换公式⎪⎪⎪⎭⎪⎪⎪⎬⎫++=++=++=213322131113322123313322112R R R R R R R R R R R R R R R R R R R R R R R R (1)Δ⇒ Y等效变换公式⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫++=++=++=312312233133123121223231231231121R R R R R R R R R R R R R R R R R R (2)3、星/网等效变化设星形网络点到中心点为()个节点(将中心点1+n o k R k n n 如图2所示。



电路等效变换的原理及应用1. 引言在电路分析中,电路等效变换是一种常见且重要的技术。
它允许我们将复杂的电路转化为简化的等效电路,从而简化分析过程并提高设计效率。
本文将介绍电路等效变换的基本原理,并探讨其在电路分析和设计中的应用。
2. 电路等效变换的基本原理电路等效变换的基本原理是基于电路中不同元件的等效关系。
通过将电阻、电容和电感等元件按照一定的规则进行等效替换,我们可以将复杂的电路简化为一个等效电路,这个等效电路具有与原电路相同的特性和行为,但更加简单和易于分析。
2.1 电阻的等效替换电路中的电阻可以通过欧姆定律进行等效替换。
欧姆定律表明,电阻与电流和电压之间存在线性关系,即V = IR,其中V为电阻两端的电压,I为通过电阻的电流,R为电阻的阻值。
因此,我们可以将电阻简化为一个等效电阻,其阻值与原电路中的电阻相同。
2.2 电容的等效替换电路中的电容可以通过等效电容进行替换。
等效电容是一个具有与原电容相同等效电容值的电路元件。
在稳态情况下,电容器的电压不发生变化,因此可以将电容简化为一个等效电容,其电容值与原电路中的电容相同。
2.3 电感的等效替换电路中的电感可以通过等效电感进行替换。
等效电感是一个具有与原电感相同等效电感值的电路元件。
在稳态情况下,电感器中的电流不发生变化,因此可以将电感简化为一个等效电感,其电感值与原电路中的电感相同。
3. 电路等效变换的应用电路等效变换在电路分析和设计中有着广泛的应用。
下面将介绍其在以下几个方面的具体应用:3.1 电路分析电路等效变换在电路分析中起到简化复杂电路的作用。
通过将复杂的电路转化为简化的等效电路,我们可以减少分析过程中的计算量,使得分析更加简单和高效。
3.2 电路设计在电路设计中,电路等效变换可以帮助我们优化电路结构。
通过将电路中的一些元件进行等效替换,可以实现电路的简化和优化,从而提高电路的性能和效率。
3.3 故障诊断电路等效变换在故障诊断中也有应用。



电路等效变换引言电路等效变换是电路分析中的一种重要方法,通过将电路中的一些元件或电路结构进行变换,可以简化复杂的电路,使其更容易分析和计算。
本文将介绍电路等效变换的基本概念和常用方法,以及它在电路分析中的应用。
电路等效变换的基本概念电路等效变换是指在不改变电路的总体功能和性质的前提下,通过对电路进行一系列变换,将原有电路等效为一个简单、方便分析的等效电路。
等效电路与原有电路在某些方面有着相同的性质,可以用来进行电路计算和分析。
常用的电路等效变换方法1. 串、并联电阻的等效变换•串联电阻的等效变换:将串联电阻变换为等效电阻,其阻值等于串联电阻的和。
•并联电阻的等效变换:将并联电阻变换为等效电阻,其阻值等于并联电阻的倒数之和的倒数。
2. 电压源与电流源的等效变换•电压源的等效变换:将电压源变换为等效电流源,其电流等于电压除以等效电阻。
•电流源的等效变换:将电流源变换为等效电压源,其电压等于电流乘以等效电阻。
3. 零电阻与无穷大电阻的等效变换•零电阻的等效变换:将零电阻变换为等效电流源,其电流等于零。
•无穷大电阻的等效变换:将无穷大电阻变换为等效电压源,其电压等于无穷大。
4. 串并联电感和电容的等效变换•串联电感的等效变换:将串联电感变换为等效电感,其电感等于串联电感的和。
•并联电感的等效变换:将并联电感变换为等效电感,其电感等于并联电感的倒数之和的倒数。
•串联电容的等效变换:将串联电容变换为等效电容,其电容等于串联电容的倒数之和的倒数。
•并联电容的等效变换:将并联电容变换为等效电容,其电容等于并联电容的和。
电路等效变换的应用电路等效变换在电路分析和设计中具有广泛的应用。
它可以简化复杂的电路,使电路的分析和计算更加方便。
以下是电路等效变换的一些常见应用:1. 电路简化通过对电路进行等效变换,可以将复杂的电路简化为简单的等效电路,从而减少计算和分析的复杂程度。
2. 电路分析通过对电路中的元件进行等效变换,可以将原始电路转化为等效电路,从而更方便地进行电路分析和计算。
XXX 实验室学生实验报告课程名称电路分析基础实验学院XXX专业XXX班级XXX学号XXX姓名XXX辅导教师XXX实验时间:X 年X 月X 日预 习 实 验 报 告1、 实验名称电压源、电流源及其电源等效变换2、实验目的1.掌握建立电源模型的方法。
2.掌握电源外特性的测试方法。
3.加深对电压源和电流源特性的理解。
4.研究电源模型等效变换的条件。
3、实验内容1.电压源和电流源电压源具有端电压保持恒定不变,而输出电流的大小由负载决定的特性。
其外特性,即端电压U 与输出电流I 的关系U = f (I ) 是一条平行于I轴的直线。
实验中使用的恒压源在规定的电流范围内,具有很小的内阻,可以将它视为一个电压源。
电流源具有输出电流保持恒定不变,而端电压的大小由负载决定的特性。
其外特性,即输出电流I 与端电压U 的关系I = f (U ) 是一条平行于U 轴的直线。
实验中使用的恒流源在规定的电流范围内,具有极大的内阻,可以将它视为一个电流源。
2.实际电压源和实际电流源实际上任何电源内部都存在电阻,通常称为内阻。
因而,实际电压源可以用一个内阻R S 和电压源U S 串联表示,其端电压U 随输出电流I 增大而降低。
在实验中,可以用一个小阻值的电阻与恒压源相串联来模拟一个实际电压源。
实际电流源是用一个内阻R S 和电流源I S 并联表示,其输出电流I 随端电压U 增大而减小。
在实验中,可以用一个大阻值的电阻与恒流源相并联来模拟一个实际电流源。
3.实际电压源和实际电流源的等效互换一个实际的电源,就其外部特性而言,既可以看成是一个电压源,又可以看成是一个电流源。
若视为电压源,则可用一个电压源U s 与一个电阻R S 相串联表示;若视为电流源,则可用一个电流源I S 与一个电阻R S 相并联来表示。
若它们向同样大小的负载供出同样大小的电流和端电压,则称这两个电源是等效的,即具有相同的外特性。
实际电压源与实际电流源等效变换的条件为: (1)取实际电压源与实际电流源的内阻均为R S ;(2)已知实际电压源的参数为U s 和R S ,则实际电流源的参数为SS S R UI =和R S ,若已知实际电流源的参数为I s 和R S ,则实际电压源的参数为S S S R I U =和R S 。