高中立体几何测试题(文科)

立体几何（文科综合）1．如图, 在四棱锥P ABCD 中,四边形ABCD 是直角梯形, DC 2AD 2AB 2，DAB ADC 90 , PB 2，PDC 为等边三角形.1）证明：PD BC ；2）求点B到平面PCD的距离.答案】（1）略；（2）632．如图，圆锥PO中，AB是圆O的直径，C是底面圆O上一点，且CAB ，点D为半径OB的中6（Ⅰ）求证：CD 平面APB ；（Ⅱ）当APB是边长为4的正三角形时，求点A到平面PBC的距离. 【答案】（Ⅰ）见证明；（Ⅱ）h 4 1553．如图，已知在直四棱柱ABCD A1 B1C1D1 中，AD DC ，AB/ /DC ，DC DD1 2AD 2AB 2 ．（1）求证：DB 平面B1BCC1 ；（2）求点A1到平面C1BD 的距离．【答案】（1）证明见解析；（2）3. 4．如图，四棱锥的底面是直角梯形，点，。

1）证明：平面2）求点到平面的距离。

答案】（ 1 ）见解析；（ 2 ）1）证明：平面平面2）求点到平面的距离.答案】（1）见解析（2）6．如图所示，在三棱锥D－ABC中，AC，BC，CD两两垂直，AC＝CD＝1，＝，O为AB 的中点．平面的中5．如图，在三棱柱，是边的中点.中（底面为正三角形），平面说明点 M ， N 的位置 （ 不要求证明 ）；（2） 求点 C 到平面 ABD 的距离．【答案】（ 1）见解析；（ 2）（1） 求证： CF ∥平面 ； （2） 求三棱锥 C － 的高．【答案】（ 1）见解析；（ 2）求证：平面 平面，求点 到平面 的距离与平面 ACD 平行，且与棱 DB ，CB 分别相交于 M ， N ，在图中画出该截面多边形，并在 的条件下，若 ，求 与平面 所成角的正切值的侧棱 AA1⊥底面 ABC ，∠ACB ＝90°， E 是棱 的中点， F 是 AB 的中点，8．已知四棱锥的底面 是菱形， 底面 是 上的任意一点7．如图，三棱柱 ABC －答案】（ 1）见解析（ 2） （3）9．如图， 已知 平面 ， 为矩形， 、 分别为 、 的中点，1）求证： 平面 ；2）求证：面平面3）求点 到平面 的距离 .答案】（ 1）证明见解析； （2）证明见解析； （3） .1）证明： 平面答案】（ 1）证明见解析； （2）11．在长方体 ABCD A 1BC 1 1D 1 中，底面 ABCD 是边长为 2的正方形， AA 1=2 3，E 是 AB 的中点， F10．如图，在四棱锥 点 Q 在棱 AB中， 平面的体积为，求点 B 到平面 PDQ 的距离 .是 BB 1 的中点1）求证：EF / / 平面A1DC1；2）求点A到平面A1DC1 的距离.答案】（1）见解析（2） 2 217ADFC是边长为2的正方形，点M 是棱EF 的中点.2）若三棱锥B DEF 的体积为4，求点B到平面ADFC 的距离.答案】（1）见解析（2）613．已知四棱锥P ABCD的底面为菱形，且ABC 60 ，AB PC 2,AP BP 2 .1）求证：平面PAB 平面ABCD ；2）求点D 到平面APC的距离.答案】（1）证明见解析；（2） 2 21714．如图，在等腰梯形ABCD中，AB/ /CD ，AD DC CB CF ，ABC 60 ，四边形ACFE为平行四边形，FC 平面ABCD ，点M 为线段EF 中点.1）求证： BC ⊥平面 ACFE ；2）若 AD 2，求点 A 到平面 MBC 的距离 答案】（ 1）详见解析； （ 2） 4 21 .715．如图所示，在梯形 ABCD 中， AD ∥ BC ，AB ⊥BC ，AB BC 1， PA ⊥平面 ABCD ， CD ⊥2）若 PA AD ，求点 B 到平面 PAC 的距离．答案】（ 1）见解析（ 2） 16．如图， 在直三棱柱 ABC-A 1B 1C 1 中， ABC 为正三角形， AB=AA=1 2 ， M 是 A 1C 的中点， N 是 A 1B 1 的中点1）证明：MN ∥ 平面 BCC 1B 1 ； 2）求点 M 到平面 ACB 1的距离 .PAC ；【答案】（ 1）见证明；（2） 21717．如图，在底面是正方形的四棱锥P ABCD 中， PA 平面 ABCD ， BD 交 AC 于点 E , F 是 PA 的中点， G 为 AC 上一动点．1）求证： BD FG ；2）若 G 是AE 的中点， PA AB 4，求点 P 到平面 FGD 的距离. 答案】（1）证明见解析； （2） 2 14.718．如图，四面体 ABCD 中， O 、 E 分别是 BD 、BC 的中点，1）求证： AO 平面 BCD ；2）求异面直线 AB 与 CD 所成角的余弦值； 3）求点 E 到平面 ACD 的距离。

立体几何基础检测卷（文科）一、选择题（每题4分）1.用a ，b ，c 表示三条不同的直线，γ表示平面，给出下列命题：①若a ∥b ，b ∥c ，则a ∥c ； ②若a ⊥b ，b ⊥c ，则a ⊥c ；③若a ∥γ，b ∥γ，则a ∥b ； ④若a ⊥γ，b ⊥γ，则a ∥b ．其中真命题的序号是（ ）A ．①②B ．②③C ．①④D ．③④2.已知l ，m ，n 为三条不同直线，α，β，γ为三个不同平面，则下列判断正确的是（） A ．若m ∥α，n ∥α，则m ∥nB ．若m ⊥α，n ∥β，α⊥β，则m ⊥nC ．若α∩β=l ，m ∥α，m ∥β，则m ∥lD ．若α∩β=m ，α∩γ=n ，l ⊥m ，l ⊥n ，则l ⊥α3.一个几何体的三视图如图1所示，其中正视图是一个正三角形，则该几何体的体积为( ).A ．1BC D4.一个几何体的三视图如图所示，则该几何体的体积为A. 64B. 72C. 80D.1125.一个棱锥的三视图如图所示，则它的体积为 ( )A ．B ．C ．1D ． 1232136、长方体的一个顶点上三条棱长为3、4、5，且它的八个顶点都在一个球面上，这个球的表面积是（ ）A ．20πB ．25πC ．50πD ．200π7、一个圆锥的表面积为，它的侧面展开图是圆心角为的扇形，则该圆锥的高为（ ）A ．1 B．2 D．8、教室内有一把尺子无论怎样放置，地面上总有这样的直线与该直尺所在直线 （ ）A ．垂直B ．平行C ．异面D ．相交但不垂直9、过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为（）（A ）316 （B ） 916 （C ） 38 （D ） 93210、.如图，在棱长为a 的正方体1111D C B A ABCD -中,P 为11D A 的中点,Q 为11B A 上任意一点,F E 、为CD 上两点,且EF 的长为定值,则下面四个值中不是定值的是（ ）(A)点P 到平面QEF 的距离 (B)直线PQ 与平面PEF 所成的角(C)三棱锥QEF P -的体积 (D)QEF ∆的面积二、填空题（每题4分）1.若某几何体的三视图 (单位：cm) 如图所示，则此几何体的表面积是 cm 2．2.某几何体的三视图如图，则它的体积是________ π1203、已知正四棱锥的底面边长为2，则该正四棱锥的体积为 ．4.设α，β为互不重合的平面，m ，n 为互不重合的直线，给出下列四个命题：①若m ⊥n ，n 是平面α内任意的直线，则m ⊥α； ②若α⊥β，α∩β=m ，n ⊂α，n ⊥m 则n ⊥β； ③若α∩β=m ，n ⊂α，n ⊥m ，则α⊥β； ④若m ⊥α，α⊥β，m ∥n ，则n ∥β．其中正确命题的序号为 ．5.给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是 ．三、解答题（每小题10分）1．如图所示， PA ⊥矩形ABCD 所在的平面， ,M N 分别是AB PC 、的中点.（1）求证： //MN 平面PAD .（2）MN CD ⊥2．如图，已知PA O ⊥所在的平面， AB 是O 的直径， 4,AB C =是O 上一点，且0,45,AC BC PCA E =∠=是PC 中点， F 为PB 中点．（1）求证： //EF 面ABC ；（2）求证： EF ⊥面PAC ；（3）求三棱锥B PAC -的体积．3．如图，四棱锥P ABCD -的底面ABCD 是菱形， 060BCD ∠=， PA ⊥平面ABCD ， E 是AB 的中点.（1）求证：平面PDE ⊥平面PAB ；（2）棱PC 上是否存在一点F ，使得//BF 平面PDE ？若存在，确定F 的位置并加以证明；若不存在，请说明理由.4、如图所示，在四棱锥S﹣ABCD中，底面ABCD是矩形，侧面SDC⊥底面ABCD，且AB=2，SC=SD=．（1）求证：平面SAD⊥平面SBC；（2）若BC=2，求点A到平面SBD的距离h的值．立体几何基础检测卷（文科）一、选择题（每题4分）1.用a ，b ，c 表示三条不同的直线，γ表示平面，给出下列命题：①若a ∥b ，b ∥c ，则a ∥c ； ②若a ⊥b ，b ⊥c ，则a ⊥c ；③若a ∥γ，b ∥γ，则a ∥b ； ④若a ⊥γ，b ⊥γ，则a ∥b ．其中真命题的序号是（ ）A ．①②B ．②③C ．①④D ．③④答案：.C2.已知l ，m ，n 为三条不同直线，α，β，γ为三个不同平面，则下列判断正确的是（） A ．若m ∥α，n ∥α，则m ∥nB ．若m ⊥α，n ∥β，α⊥β，则m ⊥nC ．若α∩β=l ，m ∥α，m ∥β，则m ∥lD ．若α∩β=m ，α∩γ=n ，l ⊥m ，l ⊥n ，则l ⊥α答案：C3.一个几何体的三视图如图1所示，其中正视图是一个正三角形，则该几何体的体积为( ).A ．1B ．3CD ．3答案：.B4.一个几何体的三视图如图所示，则该几何体的体积为A. 64B. 72C. 80D.112答案 .C5.一个棱锥的三视图如图所示，则它的体积为 ( )A ．B ．C ．1D ．答案：.A6、长方体的一个顶点上三条棱长为3、4、5，且它的八个顶点都在一个球面上，这个球的表面积是（ ）A ．20πB ．25πC ．50πD ．200π答案：.C7、一个圆锥的表面积为，它的侧面展开图是圆心角为的扇形，则该圆锥的高为（ ）A ．1 B．2 D． 答案：.B8、教室内有一把尺子无论怎样放置，地面上总有这样的直线与该直尺所在直线 （ ）A ．垂直B ．平行C ．异面D ．相交但不垂直答案：.A9、过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为（ ）（A ）316 （B ） 916 （C ） 38 （D ） 932答案：.A 10、.如图，在棱长为a 的正方体1111D C B A ABCD -中,P 为11D A 的中点,Q 为11B A 上任意一点,F E 、为CD 上两点,且EF 的长为定值,则下面四个值中不是定值的是（ ）(A)点P 到平面QEF 的距离 (B)直线PQ 与平面PEF 所成的角(C)三棱锥QEF P -的体积 (D)QEF ∆的面积答案：.B二、填空题（每题4分）1.若某几何体的三视图 (单位：cm) 如图所示，则此几何体的表面积是 cm 2． 123213π120答案：.2.某几何体的三视图如图，则它的体积是________答案：.2 83π-3、已知正四棱锥的底面边长为2，则该正四棱锥的体积为．答案：8 34.设α，β为互不重合的平面，m，n为互不重合的直线，给出下列四个命题：①若m⊥n，n是平面α内任意的直线，则m⊥α；②若α⊥β，α∩β=m，n⊂α，n⊥m则n⊥β；③若α∩β=m，n⊂α，n⊥m，则α⊥β；④若m⊥α，α⊥β，m∥n，则n∥β．其中正确命题的序号为．答案：①②5.给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是．答案：.②④三、解答题（每小题10分）1．如图所示， PA ⊥矩形ABCD 所在的平面， ,M N 分别是AB PC 、的中点.（1）求证： //MN 平面PAD .（2）MN CD ⊥解析：（1）证明：取PD 的中点E ，连接,AE EN ,,E N 分别是,PC PD 的中点,1//2EN CD ∴, //AM EN ∴,∴四边形AMNE 是平行四边形， //MN AE ∴ MN ⊄平面PAD ， AD ⊂平面PAD ,∴ //MN 平面PAD .（2） PA ⊥平面ABCD ， ∴ PA CD ⊥,又CD AD ⊥,∴ CD ⊥平面PAD ,∴ CD AE ⊥,又//MN AE ， CD MN ∴⊥.2．如图，已知PA O ⊥所在的平面， AB 是O 的直径， 4,AB C =是O 上一点，且0,45,AC BC PCA E =∠=是PC 中点， F 为PB 中点．（1）求证： //EF 面ABC ；（2）求证： EF ⊥面PAC ；（3）求三棱锥B PAC -的体积．试题解析：（1）证明：在三角形PBC 中， E 是PC 中点， F 为PB 中点，∴//EF BC ， BC ⊂平面,ABC EF ⊄平面ABC ，∴//EF 面ABC ；（2）证明：∵PA ⊥面ABC ， BC ⊂平面ABC ，∴BC PA ⊥，又∵AB 是O 的直径，∴BC AC ⊥，又PA AC A ⋂=，∴BC ⊥面PAC ，∵//EF BC ，∴EF ⊥面PAC ；（3）∵045PCA ∠=，∴PA AC =，在Rt ABC ∆中，∵,4AC BC AB ==，∴AC BC ==∴1·33B PAC P ABC ABC V V S PA --∆===． 3．如图，四棱锥P ABCD -的底面ABCD 是菱形， 060BCD ∠=， PA ⊥平面ABCD ，E 是AB 的中点.（1）求证：平面PDE ⊥平面PAB ；（2）棱PC 上是否存在一点F ，使得//BF 平面PDE ？若存在，确定F 的位置并加以证明；若不存在，请说明理由.解析：（1）连接BD ，因为底面ABCD 是菱形， 60BCD ∠=︒,所以ABD ∆为正三角形.因为E 是AB 的中点, 所以DE AB ⊥,因为PA ⊥面ABCD , DE ABCD ⊂面，∴DE PA ⊥，因为DE AB ⊥， DE PA ⊥， AB PA A ⋂=,所以DE PAB ⊥面.又DE PDE ⊂面, 所以面PDE ⊥面PAB .（2）当点F为PC的中点时，BF∥面PDE.事实上，取PC的中点F,PD的中点G，连结FG，GE，∵FG为三角形PCD的中位线，∴FG∥CD且1=2FG CD，又在菱形ABCD中，E为AB的中点，∴BE∥CD且1=2BE CD，∴FG∥BE且=FG BE，所以四边形BEGF为平行四边形.所以BF∥GE，又GE⊂面PDE，BF⊄面PDE，∴BF∥面PDE，结论得证.4、如图所示，在四棱锥S﹣ABCD中，底面ABCD是矩形，侧面SDC⊥底面ABCD，且AB=2，SC=SD=．（1）求证：平面SAD⊥平面SBC；（2）若BC=2，求点A到平面SBD的距离h的值．【解答】（1）证明：侧面SDC⊥底面ABCD，有AD⊥SC，AD⊥SD故△ADS为Rt△，有SD2+AD2=SA2且AD=BC，SD=，故2+BC2=SA2即BC2=SA2﹣2连接AC，易得AC2=BC2+AB2=BC2+4即BC2=AC2﹣4那么SA2﹣2=AC2﹣4，整理后有AC2=SA2+2又SC=，故AC2=SA2+SC2所以△ASC为Rt△，有SA⊥SC所以SC⊥平面SAD，那么平面SBC⊥平面SAD；（2）解：由题意，BC⊥SC，SB=，DB=2，∴DB2=SD2+SB2，∴SB⊥SD，∴S△SBD==．由等体积可得，∴h=，即点A到平面SBD的距离h的值为．。

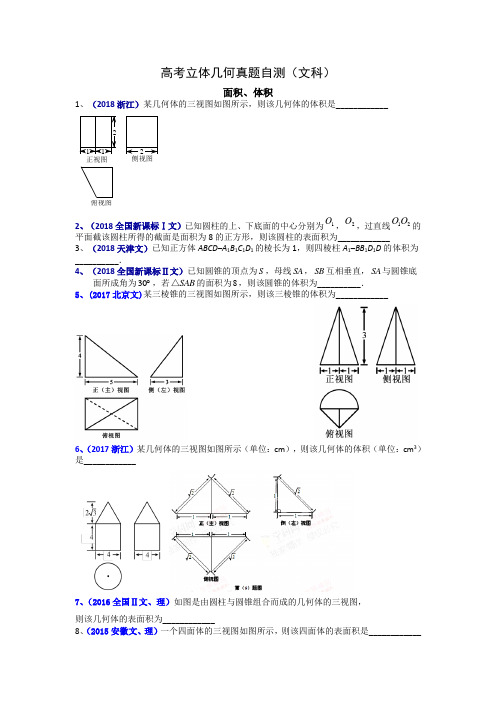
高考立体几何真题自测（文科）面积、体积1、（2018浙江）某几何体的三视图如图所示，则该几何体的体积是____________ 俯视图正视图22112、（2018全国新课标Ⅰ文）已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为____________ 3、（2018天津文）已知正方体ABCD –A 1B 1C 1D 1的棱长为1，则四棱柱A 1–BB1D 1D 的体积为__________．4、（2018全国新课标Ⅱ文）已知圆锥的顶点为S ，母线SA ，SB 互相垂直，SA 与圆锥底面所成角为30 ，若SAB △的面积为8，则该圆锥的体积为__________．5、(2017北京文)某三棱锥的三视图如图所示，则该三棱锥的体积为____________6、（2017浙江）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是____________7、（2016全国Ⅱ文、理）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为____________8、（2015安徽文、理）一个四面体的三视图如图所示，则该四面体的表面积是____________空间角9、（2018全国新课标Ⅰ文）在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30︒，则该长方体的体积为________10、（2018全国新课标Ⅱ文）在正方体1111ABCD A B C D -中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为________11、（2017全国新课标Ⅱ理）已知直三棱柱111C C AB -A B 中，C 120∠AB =，2AB =，1C CC 1B ==，则异面直线1AB 与1C B 所成角的余弦值为________12、（2016全国Ⅰ文、理）平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α//平面CB 1D 1, ABCD m α=平面,11ABB A n α=平面，则m 、n 所成角的正弦值为________ 平行、垂直13、（2017全国新课标Ⅲ文）在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则（ ）A ．11A E DC ⊥B ．1A E BD ⊥C ．11A E BC ⊥D ．1AE AC ⊥14、（2016浙江文、理） 已知互相垂直的平面αβ，交于直线l .若直线m ，n 满足,m n αβ∥⊥， 则（ ）A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n15、（2016全国Ⅱ理）,αβ是两个平面，,m n 是两条直线，有下列四个命题：（1）如果,,//m n m n αβ⊥⊥，那么αβ⊥.（2）如果,//m n αα⊥，那么m n ⊥.（3）如果//,m αβα⊂，那么//m β.（4）如果//,//m n αβ，那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有 ． (填写所有正确命题的编号）16、(2015浙江文)设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂（ ）A ．若l β⊥，则αβ⊥B ．若αβ⊥，则l m ⊥C ．若//l β，则//αβD ．若//αβ，则//l m球17、（2017全国新课标Ⅲ理）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（ ）A ．πB ．3π4C ．π２D ．π418、（2017全国新课标Ⅱ文）长方体的长，宽，高分别为3,2,1，其顶点都在球O 的球面上，则球O 的表面积为 .19、（2017天津文、理）已知一个正方形的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为 ______.20、（2016全国Ⅱ文）体积为8的正方体的顶点都在同一球面上，则该球面的表面积为______.。

高中数学《立体几何》练习题1．用斜二测画法画出长为6，宽为4的矩形水平放置的直观图，则该直观图面积为 ( ) A.12 B.24 C.62 D.1222．设,m n 是不同的直线，,αβ是不同的平面，下列命题中正确的是 ( ) A ．若//,,m n m n αβ⊥⊥，则αβ⊥ B ．若//,,m n m n αβ⊥⊥，则//αβ C ．若//,,//m n m n αβ⊥，则α⊥β D ．若//,,//m n m n αβ⊥，则//αβ3．如图，棱长为1的正方体1111D C B A ABCD -中，P 为线段B A 1上的动点，则下列结论错误．．的是A ．P D DC 11⊥B ．平面⊥P A D 11平面AP A 1C ．1APD ∠的最大值为090 D ．1PD AP +的最小值为22+4．一个几何体的三视图如图所示(单位：m)，则该几何体的体积为______m 3.5．若某几何体的三视图如图所示，则此几何体的体积等于 .6．如图是一个几何体的三视图，则该几何体的体积是____________7．如图，一个盛满水的三棱锥容器，不久发现三条侧棱上各有一个小洞F E D ,,，且知1:2:::===FS CF EB SE DA SD ，若仍用这个容器盛水，则最多可盛水的体积是原来的 .8．如图，四边形ABCD 为正方形，QA ⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝12PD.(1)证明：PQ ⊥平面DCQ ；(2)求棱锥Q ­ABCD 的体积与棱锥P ­DCQ 的体积的比值．[来9．如图所示的多面体中，ABCD 是菱形，BDEF 是矩形，ED ⊥面ABCD ,3BAD π∠=．（1）求证://BCF AED 平面平面.（2）若,BF BD a A BDEF ==-求四棱锥的体积。

10．在四棱锥ABCD P -中，底面ABCD 为矩形，ABCD PD 底面⊥，1=AB ，2=BC ，3=PD ，FG 、分别为CD AP 、的中点． (1) 求证：PC AD ⊥；(2) 求证：//FG 平面BCP ；SFCB AD EF GPDCBA11．如图，多面体AEDBFC 的直观图及三视图如图所示，N M ,分别为BC AF ,的中点． （1）求证：//MN 平面CDEF ； (2）求多面体CDEF A -的体积．NMFEDCBA直观图俯视图正视图侧视图22222212．如图，在三棱锥P ABC -中，90ABC ∠=，PA ⊥平面ABC ，E ,F 分别为PB ,PC 的中点. （1）求证：//EF 平面ABC ；（2）求证：平面AEF ⊥平面PAB .A13．如图，在三棱锥P —ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点．已知PA ⊥AC ，PA=6，BC=8,DF=5.求证：（1）直线PA ∥平面DFE ； （2）平面BDE ⊥平面ABC ．14．如图. 直三棱柱ABC —A 1B 1C 1 中，A 1B 1= A 1C 1,点D 、E 分别是棱BC ，CC 1上的点（点D 不同于点C ），且AD ⊥DE ，F 为B 1C 1的中点． 求证：（1）平面ADE ⊥平面BCC 1B 1 （2）直线A 1F ∥平面ADE ．BA 1C 1 E C DAB 1F参考答案1．C 【解析】试题分析：斜二测法：要求长边，宽减半，直角变为045角，则面积为：2645sin 260=⨯⨯. 考点：直观图与立体图的大小关系.2．C 【解析】试题分析：此题只要举出反例即可，A,B 中由n m n ⊥⊥,β可得β//n ,则α,β可以为任意角度的两平面,A,B 均错误.C,D 中由n m n //,β⊥可得β⊥m ，则有βα//,故C 正确，D 错误.考点：线，面位置关系. 3．C 【解析】试题分析：⊥1DC 面11BCD A ，∴A 正确；⊥11A D 面11A ABB ，∴B 正确；当2201<<P A 时，1APD ∠为钝角，∴C 错；将面B AA 1与面11A ABB 沿B A 1展成平面图形，线段D A 1即为1PD AP +的最小值，解三角形易得D A 1=22+， ∴D 正确.故选C. 考点：线线垂直、线面垂直、面面垂直. 4．4 【解析】试题分析：已知三视图对应的几何体的直观图，如图所示：，所以其体积为：4211112=⨯⨯+⨯⨯=V ，故应填入：４． 考点：三视图． 5．24 【解析】试题分析：由三视图可知，原几何体是一个三棱柱被截去了一个小三棱锥得到的，如图111345(34)324232V =⨯⨯⨯-⨯⨯⨯=.考点：三视图. 【答案】12 【解析】试题分析：该几何体是一个直三棱柱，底面是等腰直角三角形 体积为12262V =⨯⨯⨯＝12考点：三视图，几何体的体积. 7．2723 【解析】试题分析：过DE 作截面平行于平面ABC ,可得截面下体积为原体积的27193213=-）（，若过点F ，作截面平行于平面SAB ,可得截面上的体积为原体积的278323=）（，若C 为最低点，以平面DEF 为水平上面，则体积为原体积的27233132321=⨯⨯-，此时体积最大. 考点：体积相似计算. 8．(1)祥见解析； (2)１． 【解析】试题分析：(1)要证直线与平面垂直，只须证明直线与平面内的两条相交直线垂直即可，注意到QA ⊥平面ABCD ，所以有平面PDAQ ⊥平面ABCD ，且交线为AD ，又因为四边形ABCD 为正方形，由面面垂直的性质可得DC ⊥平面PDAQ ，从而有PQ ⊥DC ，又因为PD ∥QA ，且QA ＝AB ＝12PD ，所以四边形PDAQ 为直角梯形，利用勾股定理的逆定理可证PQ ⊥QD ；从而可证 PQ ⊥平面DCQ ；(2)设AB ＝a ，则由(1)及已知条件可用含a 的式子表示出棱锥Q －ABCD 的体积和棱锥P －DCQ 的体积从而就可求出其比值． 试题解析：(1)证明：由条件知PDAQ 为直角梯形．因为QA ⊥平面ABCD ，所以平面PDAQ ⊥平面ABCD ，交线为AD. 又四边形ABCD 为正方形，DC ⊥AD ， 所以DC ⊥平面PDAQ.可得PQ ⊥DC.在直角梯形PDAQ 中可得DQ ＝PQ ， 则PQ ⊥QD.所以PQ ⊥平面DCQ.(2)设AB ＝a.由题设知AQ 为棱锥Q ­ABCD 的高，所以棱锥Q －ABCD 的体积V 1＝13a 3.由(1)知PQ 为棱锥P －DCQ 的高，而PQ a ，△DCQ 的面积为2a 2， 所以棱锥P －DCQ 的体积V 2＝13a 3. 故棱锥Q －ABCD 的体积与棱锥P －DCQ 的体积的比值为1. 考点：１．线面垂直；２．几何体的体积．9．（1）证明过程详见解析；（2）36a . 【解析】试题分析：本题主要考查线线平行、线面平行、面面平行、四棱锥的体积等基础知识，考查学生的空间想象能力、逻辑推理能力、计算能力.第一问，由于ABCD 是菱形，得到//BC AD ，利用线面平行的判定，得//BC ADE 面，由于BDEF 为矩形，得BF//DE ，同理可得BF//面ADE ，利用面面平行的判定，得到面BCF//面AED ；第二问，通过证明得到AO BDEF ⊥面，则AO 为四棱锥A BDEF -的高，再求出BDEF 的面积，最后利用体积公式13V Sh =，计算四棱锥A-BDEF 的体积.试题解析：证明：（1）由ABCD 是菱形 //BC AD ∴,BC ADE AD ADE ⊄⊂面面 //BC ADE ∴面 3分由BDEF 是矩形//BF DE ∴,BF ADE DE ADE ⊄⊂面面 //BF ADE ∴面,,BC BCF BF BCF BCBF B ⊂⊂=面面∴//BCF AED 平面平面. 6分 （2）连接AC ，ACBD O =由ABCD 是菱形， AC BD ∴⊥由ED ⊥面ABCD ,AC ABCD ⊂面 ED AC ∴⊥,,ED BD BDEF EDBD D ⊂=面 AO BDEF ∴⊥面， 10分则AO 为四棱锥A BDEF -的高 由ABCD 是菱形，3BAD π∠=，则ABD ∆为等边三角形，由BF BD a ==；则3,2AD a AO a ==，2BDEF S a =， 23133326A BDEF V a a a -=⋅⋅=14分考点：线线平行、线面平行、面面平行、四棱锥的体积.10．(1)见解析；(2)见解析.【解析】 试题分析：（1）欲证线线垂直往往通过证明线面垂直（即证明其中一条线垂直于另一条所在平面）；（2）欲证线面平行，需在平面内寻找一条直线，并证此线平行于另一直线.此题也可以采用空间向量证明，即证明FG 的方向向量垂直于平面BCP 的法向量n 即可. 试题解析：（1）证明： 底面ABCD 为矩形 CD AD ⊥∴ABCD AD ABCD PD 平面底面⊂⊥ , PD AD ⊥∴D PD CD = PDC AD 平面⊥∴ABCD PC 平面⊂ PC AD ⊥∴H F GPD CBA（2）证明：取H BP 中点，连接CH GH ,中点分别为DC AP F G ,,GH ∴=//AB 21,FC =//AB 21 GH ∴=//FC GFCH 四边形∴是平行四边形， FG ∴//CH ，BCP CH 平面⊂，BCP FG 平面⊄ FG ∴//BCP 平面考点：（1）线线垂直；（2）线面平面.11．（1）证明：见解析；（2）多面体CDEF A -的体积83．【解析】试题分析： （1）由多面体AEDBFC 的三视图知，三棱柱BFC AED -中,底面DAE 是等腰直角三角形，2==AE DA ，⊥DA 平面ABEF ,侧面ABCD ABFE ,都是边长为2的正方形．连结EB ，则M 是EB 的中点，由三角形中位线定理得EC MN //，得证. （2）利用⊥DA 平面ABEF ，得到EF AD ⊥, 再据EF ⊥AE ，得到EF ⊥平面ADE ，从而可得：四边形 CDEF 是矩形,且侧面CDEF ⊥平面DAE .取DE 的中点,H得到AH =且⊥AH 平面CDEF ．利用体积公式计算.所以多面体CDEF A -的体积383131=⋅⋅=⋅=AH EF DE AH S V CDEF ． 12分 试题解析： （1）证明：由多面体AEDBFC 的三视图知，三棱柱BFC AED -中,底面DAE 是等腰直角三角形，2==AE DA ，⊥DA 平面ABEF ,侧面ABCD ABFE ,都是边长为2的 正方形．连结EB ，则M 是EB 的中点， 在△EBC 中，EC MN //，且EC ⊂平面CDEF ，MN ⊄平面CDEF ， ∴MN ∥平面CDEF ． 6分FDA（2）因为⊥DA 平面ABEF ，EF ⊂平面ABEF , AD EF ⊥∴,又EF ⊥AE ，所以，EF ⊥平面ADE ，∴四边形 CDEF 是矩形,且侧面CDEF ⊥平面DAE 8分 取DE 的中点,H ⊥DA ,AE 2==AE DA ,2=∴AH ,且⊥AH 平面CDEF ． 10分所以多面体CDEF A -的体积383131=⋅⋅=⋅=AH EF DE AH S V CDEF ． 12分 考点：三视图，平行关系，垂直关系，几何体的体积. 12．（1）见解析；（2）见解析 【解析】 试题分析：（1）由E 、F 分别为PB 、PC 中点根据三角形中位线定理知EF ∥BC ，根据线面平行的判定知EF ∥面ABC ；（2）由PA ⊥面PABC 知，PA ⊥BC ，结合AB ⊥BC ，由线面垂直的判定定理知，BC ⊥面PAB ，由（1）知EF ∥BC ，根据线面垂直性质有EF ⊥面PAB ，再由面面垂直判定定理即可证明面AEF ⊥面PAB.试题解析：证明:（1）在PBC ∆中，F E , 分别为PC PB ,的中点BC EF //∴ 3分 又⊂BC 平面ABC ，⊄EF 平面ABC //EF ∴平面ABC 7分 （2）由条件，⊥PA 平面ABC ，⊂BC 平面ABCBC PA ⊥∴︒=∠90ABC ，即BC AB ⊥， 10分 由//EF BC ，∴EF AB ⊥，EF PA ⊥又A AB PA =⋂，AB PA ,都在平面PAB 内 EF ∴⊥平面PAB又⊂EF 平面AEF ∴平面AEF ⊥平面PAB 14分考点:线面垂直的判定与性质；面面垂直判定定理；线面平行判定；推理论证能力13．(1)详见解析; (2) 详见解析. 【解析】 试题分析：(1) 由线面平行的判定定理可知,只须证PA 与平面DEF 内的某一条直线平行即可,由已知及图形可知应选择DE,由三角形的中位线的性质易知: DE ∥PA ,从而问题得证；注意线PA 在平面DEG 外,而DE 在平面DEF 内必须写清楚；(2) 由面面垂直的判定定理可知,只须证两平中的某一直线与另一个平面垂直即可，注意题中已知了线段的长度，那就要注意利用勾股定理的逆定理来证明直线与直线的垂直；通过观察可知：应选择证DE 垂直平面ABC 较好,由(1)可知:DE ⊥AC,再就只须证DE ⊥EF 即可；这样就能得到DE ⊥平面ABC ，又DE ⊂平面BDE ，从面而有平面BDE ⊥平面ABC ．试题解析：(1)因为D ，E 分别为PC,AC 的中点，所以DE ∥PA. 又因为PA ⊄平面DEF ，DE ⊂平面DEF ，所以直线PA ∥平面DEF.(2)因为D ，E ，F 分别人棱PC,AC ，AB 的中点，PA ＝6，BC ＝8，所以DE ∥PA ，DE ＝21PA ＝3，EF ＝21BC ＝4． 又因为DF ＝5，故DF 2＝DE 2+EF 2，所以∠DEF=90。

立体几何大题练习（文科）：1．如图，在四棱锥S﹣ABCD中，底面ABCD是梯形，AB∥DC，∠ABC=90°，AD=SD，BC=CD=，侧面SAD⊥底面ABCD．（1）求证：平面SBD⊥平面SAD；（2）若∠SDA=120°，且三棱锥S﹣BCD的体积为，求侧面△SAB的面积．【分析】（1）由梯形ABCD，设BC=a，则CD=a，AB=2a，运用勾股定理和余弦定理，可得AD，由线面垂直的判定定理可得BD⊥平面SAD，运用面面垂直的判定定理即可得证；（2）运用面面垂直的性质定理，以及三棱锥的体积公式，求得BC=1，运用勾股定理和余弦定理，可得SA，SB，运用三角形的面积公式，即可得到所求值．【解答】（1）证明：在梯形ABCD中，AB∥DC，∠ABC=90°，BC=CD=，设BC=a，则CD=a，AB=2a，在直角三角形BCD中，∠BCD=90°，可得BD=a，∠CBD=45°，∠ABD=45°，由余弦定理可得AD==a，则BD⊥AD，由面SAD⊥底面ABCD．可得BD⊥平面SAD，又BD⊂平面SBD，可得平面SBD⊥平面SAD；（2）解：∠SDA=120°，且三棱锥S﹣BCD的体积为，由AD=SD=a，在△SAD中，可得SA=2SDsin60°=a，△SAD的边AD上的高SH=SDsin60°=a，由SH⊥平面BCD，可得×a××a2=，解得a=1，由BD⊥平面SAD，可得BD⊥SD，SB===2a，又AB=2a，在等腰三角形SBA中，边SA上的高为=a，则△SAB的面积为×SA×a=a=．【点评】本题考查面面垂直的判定定理的运用，注意运用转化思想，考查三棱锥的体积公式的运用，以及推理能力和空间想象能力，属于中档题．2．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【分析】（1）利用AB∥EF及线面平行判定定理可得结论；（2）通过取线段CD上点G，连结FG、EG使得FG∥BC，则EG∥AC，利用线面垂直的性质定理可知FG⊥AD，结合线面垂直的判定定理可知AD⊥平面EFG，从而可得结论．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊂平面ABC，AB⊂平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．【点评】本题考查线面平行及线线垂直的判定，考查空间想象能力，考查转化思想，涉及线面平行判定定理，线面垂直的性质及判定定理，注意解题方法的积累，属于中档题．3．如图，在三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，AC⊥CB，点M和N分别是B1C1和BC的中点．（1）求证：MB∥平面AC1N；（2）求证：AC⊥MB．【分析】（1）证明MC1NB为平行四边形，所以C1N∥MB，即可证明MB∥平面AC1N；（2）证明AC⊥平面BCC1B1，即可证明AC⊥MB．【解答】证明：（1）证明：在三棱柱ABC﹣A1B1C1中，因为点M，N分别是B1C1，BC的中点，所以C1M∥BN，C1M=BN．所以MC1NB为平行四边形．所以C1N∥MB．因为C1N⊂平面AC1N，MB⊄平面AC1N，所以MB∥平面AC1N；（2）因为CC1⊥底面ABC，所以AC⊥CC1．因为AC⊥BC，BC∩CC1=C，所以AC⊥平面BCC1B1．因为MB⊂平面BCC1B1，所以AC⊥MB．【点评】本题考查线面平行的判定，考查线面垂直的判定与性质，考查学生分析解决问题的能力，属于中档题．4．如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD||BC，PD⊥底面ABCD，∠ADC=90°，AD=2BC，Q为AD的中点，M为棱PC的中点．（Ⅰ）证明：PA∥平面BMQ；（Ⅰ）已知PD=DC=AD=2，求点P到平面BMQ的距离．【分析】（1）连结AC交BQ于N，连结MN，只要证明MN∥PA，利用线面平行的判定定理可证；（2）由（1）可知，PA∥平面BMQ，所以点P到平面BMQ的距离等于点A到平面BMQ的距离．【解答】解：（1）连结AC交BQ于N，连结MN，因为∠ADC=90°，Q为AD的中点，所以N为AC的中点．…（2分）当M为PC的中点，即PM=MC时，MN为△PAC的中位线，故MN∥PA，又MN⊂平面BMQ，所以PA∥平面BMQ．…（5分）（2）由（1）可知，PA∥平面BMQ，所以点P到平面BMQ的距离等于点A到平面BMQ的距离，所以V P=V A﹣BMQ=V M﹣ABQ，﹣BMQ取CD的中点K，连结MK，所以MK∥PD，，…（7分）又PD⊥底面ABCD，所以MK⊥底面ABCD．又，PD=CD=2，所以AQ=1，BQ=2，，…（10分）=V A﹣BMQ=V M﹣ABQ=.，…（11分）所以V P﹣BMQ则点P到平面BMQ的距离d=…（12分）【点评】本题考查了线面平行的判定定理的运用以及利用三棱锥的体积求点到直线的距离．5．如图，在直三棱柱ABC﹣A1B1C1中，BC⊥AC，D，E分别是AB，AC的中点．（1）求证：B1C1∥平面A1DE；（2）求证：平面A1DE⊥平面ACC1A1．【分析】（1）证明B1C1∥DE，即可证明B1C1∥平面A1DE；（2）证明DE⊥平面ACC1A1，即可证明平面A1DE⊥平面ACC1A1．【解答】证明：（1）因为D，E分别是AB，AC的中点，所以DE∥BC，…（2分）又因为在三棱柱ABC﹣A1B1C1中，B1C1∥BC，所以B1C1∥DE…（4分）又B1C1⊄平面A1DE，DE⊂平面A1DE，所以B1C1∥平面A1DE…（6分）（2）在直三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，又DE⊂底面ABC，所以CC1⊥DE…（8分）又BC⊥AC，DE∥BC，所以DE⊥AC，…（10分）又CC1，AC⊂平面ACC1A1，且CC1∩AC=C，所以DE⊥平面ACC1A1…（12分）又DE⊂平面A1DE，所以平面A1DE⊥平面ACC1A1…（14分）【点评】本题考查线面平行、线面垂直、面面垂直的判定，考查学生分析解决问题的能力，属于中档题．6．在四棱锥P﹣ABCD中，PC⊥底面ABCD，M，N分别是PD，PA的中点，AC⊥AD，∠ACD=∠ACB=60°，PC=AC．（1）求证：PA⊥平面CMN；（2）求证：AM∥平面PBC．【分析】（1）推导出MN∥AD，PC⊥AD，AD⊥AC，从而AD⊥平面PAC，进而AD ⊥PA，MN⊥PA，再由CN⊥PA，能证明PA⊥平面CMN．（2）取CD的中点为Q，连结MQ、AQ，推导出MQ∥PC，从而MQ∥平面PBC，再求出AQ∥平面，从而平面AMQ∥平面PCB，由此能证明AM∥平面PBC．【解答】证明：（1）∵M，N分别为PD、PA的中点，∴MN为△PAD的中位线，∴MN∥AD，∵PC⊥底面ABCD，AD⊂平面ABCD，∴PC⊥AD，又∵AD⊥AC，PC∩AC=C，∴AD⊥平面PAC，∴AD⊥PA，∴MN⊥PA，又∵PC=AC，N为PA的中点，∴CN⊥PA，∵MN∩CN=N，MN⊂平面CMN，CM⊂平面CMN，∴PA⊥平面CMN．解（2）取CD的中点为Q，连结MQ、AQ，∵MQ是△PCD的中位线，∴MQ∥PC，又∵PC⊂平面PBC，MQ⊄平面PBC，∴MQ∥平面PBC，∵AD⊥AC，∠ACD=60°，∴∠ADC=30°．∴∠DAQ=∠ADC=30°，∴∠QAC=∠ACQ=60°，∴∠ACB=60°，∴AQ∥BC，∵AQ⊄平面PBC，BC⊂平面PBC，∴AQ∥平面PBC，∵MQ∩AQ=Q，∴平面AMQ∥平面PCB，∵AM⊂平面AMQ，∴AM∥平面PBC．【点评】本题考查线面垂直、线面平行的证明，考查空间中线线、线面、面面间的位置关系，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想、函数与方程思想，是中档题．7．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD=AD，E、F分别为PC、BD的中点．（1）求证：EF∥平面PAD；（2）求证：面PAB⊥平面PDC．【分析】（1）连接AC，则F是AC的中点，E为PC 的中点，证明EF∥PA，利用直线与平面平行的判定定理证明EF∥平面PAD；（2）先证明CD⊥PA，然后证明PA⊥PD．利用直线与平面垂直的判定定理证明PA⊥平面PCD，最后根据面面垂直的判定定理即可得到面PAB⊥面PDC．【解答】证明：（1）连接AC，由正方形性质可知，AC与BD相交于BD的中点F，F也为AC中点，E为PC中点．所以在△CPA中，EF∥PA，又PA⊂平面PAD，EF⊄平面PAD，所以EF∥平面PAD；（2）平面PAD⊥平面ABCD平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA正方形ABCD中CD⊥ADPA⊂平面PADCD⊂平面ABCD又，所以PA2+PD2=AD2所以△PAD是等腰直角三角形，且，即PA⊥PD．因为CD∩PD=D，且CD、PD⊂面PDC所以PA⊥面PDC又PA⊂面PAB，所以面PAB⊥面PDC．【点评】本题考查直线与平面垂直的判定，直线与平面平行的判定的应用，考查逻辑推理能力．8．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为菱形，且PA=AD=2，BD=2，E、F分别为AD、PC中点．（1）求点F到平面PAB的距离；（2）求证：平面PCE⊥平面PBC．【分析】（1）取PB的中点G，连接FG、AG，证得底面ABCD为正方形．再由中位线定理可得FG∥AE且FG=AE，四边形AEFG是平行四边形，则AG∥FE，运用线面平行的判定定理可得EF∥平面PAB，点F与点E到平面PAB的距离相等，运用线面垂直的判定和性质，证得AD⊥平面PAB，即可得到所求距离；（2）运用线面垂直的判定和性质，证得BC⊥平面PAB，EF⊥平面PBC，再由面面垂直的判定定理，即可得证．【解答】（1）解：如图，取PB的中点G，连接FG、AG，因为底面ABCD为菱形，且PA=AD=2，，所以底面ABCD为正方形．∵E、F分别为AD、PC中点，∴FG∥BC，AE∥BC，，，∴FG∥AE且FG=AE，∴四边形AEFG是平行四边形，∴AG∥FE，∵AG⊂平面PAB，EF⊄平面PAB，∴EF∥平面PAB，∴点F与点E到平面PAB的距离相等，由PA⊥平面ABCD，可得PA⊥AD，又AD⊥AB，PA∩AB=A，AD⊥平面PAB，则点F到平面PAB的距离为EA=1．（2）证明：由（1）知AG⊥PB，AG∥EF，∵PA⊥平面ABCD，∴BC⊥PA，∵BC⊥AB，AB∩BC=B，∴BC⊥平面PAB，由AG⊂平面PAB，∴BC⊥AG，又∵PB∩BC=B，∴AG⊥平面PBC，∴EF⊥平面PBC，∵EF⊂平面PCE，∴平面PCE⊥平面PBC．【点评】本题考查空间点到平面的距离，注意运用转化思想，考查线面平行和垂直的判定和性质，以及面面垂直的判定，熟练掌握定理的条件和结论是解题的关键，属于中档题．9．在四棱锥P﹣ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，DC=2AB=2AD，BC⊥PD，E，F分别是PB，BC的中点．求证：（1）PC∥平面DEF；（2）平面PBC⊥平面PBD．【分析】（1）由中位线定理可得PC∥EF，故而PC∥平面DEF；（2）由直角梯形可得BC⊥BD，结合BC⊥PD得出BC⊥平面PBD，于是平面PBC ⊥平面PBD．【解答】证明：（1）∵E，F分别是PB，BC的中点，∴PC∥EF，又PC⊄平面DEF，EF⊂平面DEF，∴PC∥平面DEF．（2）取CD的中点M，连结BM，则AB DM，又AD⊥AB，AB=AD，∴四边形ABMD是正方形，∴BM⊥CD，BM=CM=DM=1，BD=，∴BC=，∴BD2+BC2=CD2，∴BC⊥BD，又BC⊥PD，BD∩PD=D，∴BC⊥平面PBD，又BC⊂平面PBC，∴平面PBC⊥平面PBD．【点评】本题考查了线面平行，面面垂直的判定，属于中档题．10．如图，在三棱锥A﹣BCD中，E，F分别为BC，CD上的点，且BD∥平面AEF．（1）求证：EF∥平ABD面；（2）若AE⊥平面BCD，BD⊥CD，求证：平面AEF⊥平面ACD．【分析】（1）利用线面平行的性质可得BD∥EF，从而得出EF∥平面ABD；（2）由AE⊥平面BCD可得AE⊥CD，由BD⊥CD，BD∥EF可得EF⊥CD，从而有CD⊥平面AEF，故而平面AEF⊥平面ACD．【解答】证明：（1）∵BD∥平面AEF，BD⊂平面BCD，平面BCD∩平面AEF=EF，∴BD∥EF，又BD⊂平面ABD，EF⊄平面ABD，∴EF∥平ABD面．（2）∵AE⊥平面BCD，CD⊂平面BCD，∴AE⊥CD，由（1）可知BD∥EF，又BD⊥CD，∴EF⊥CD，又AE∩EF=E，AE⊂平面AEF，EF⊂平面AEF，∴CD⊥平面AEF，又CD⊂平面ACD，∴平面AEF⊥平面ACD．【点评】本题考查了线面平行、线面垂直的性质，面面垂直的判定，属于中档题．。

文科立体几何模拟试题答案一、选择题1. 若一个正方体的棱长为2cm，则其对角线的长度为？A. 2√2 cmB. 2√3 cmC. 4 cmD. √8 cm答案：B2. 一个圆锥的底面半径为3cm，高为4cm，其侧面展开图的扇形的中心角为？A. 90°B. 120°C. 150°D. 180°答案：D3. 一个球的表面积为4πR²，若该球的体积为16π，则其半径R为？A. 2B. 4C. 2√2D. √16答案：A4. 一个圆柱的底面直径为6cm，高为10cm，其侧面积为？A. 60π cm²B. 36π cm²C. 90π cm²D. 180π cm²答案：A5. 一个锥体的底面半径为r，高为h，侧面展开图是一个等腰三角形，其底边长为？A. πrB. 2πrC. √(2h² + r²)D. √(h² + 4r²)答案：D二、填空题1. 一个正方体的体积为64cm³，其棱长为______。

答案：4cm2. 一个球的体积为64π，其表面积为______。

答案：64π cm²3. 一个圆柱的底面半径为5cm，高为12cm，其体积为______。

答案：942π cm³4. 一个锥体的底面半径为3cm，高为6cm，其侧面展开图的扇形的中心角为______。

答案：120°5. 一个正四面体的边长为a，其表面积为______。

答案：√3a²三、解答题1. 一个正方体的棱长为3cm，求其内切球的体积。

解：正方体的内切球即为正方体的对角线所形成的球体，其半径r为正方体棱长的一半，即r = 3/2 cm。

根据球体体积公式V = 4/3πr³，代入r值得到V = 4/3π(3/2)³ = 9π cm³。

2. 一个圆锥的底面半径为2cm，高为5cm，求其侧面展开图的扇形的弧长。

文科立体几何大题训练1．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．2．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．3．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（Ⅰ）证明MN∥平面PAB；（Ⅱ）求四面体N﹣BCM的体积．4．如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．（1）求证：DE∥平面PBC；（2）求证：AB⊥PE；（3）求三棱锥P﹣BEC的体积．5．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，PA=AB=2，E为PA 的中点，∠BAD=60°．（Ⅰ）求证：PC∥平面EBD；（Ⅱ）求三棱锥P﹣EDC的体积．6．如图，在三棱锥D﹣ABC中，DA=DB=DC，E为AC上的一点，DE⊥平面ABC，F为AB的中点．（Ⅰ）求证：平面ABD⊥平面DEF；（Ⅱ）若AD⊥DC，AC=4，∠BAC=45°，求四面体F﹣DBC的体积．7．如图，四边形ABCD是正方形，平面ABCD⊥平面ABE，AF∥BE，AB⊥BE，AB=BE=2，AF=1．（Ⅰ）求证：AC⊥平面BDE；（Ⅱ）求证：AC∥平面DEF；（III）求三棱锥D﹣FEB的体积．8．如图，四棱锥S﹣ABCD中，底面ABCD是菱形，其对角线的交点为O，且SA=SC，SA⊥BD．（1）求证：SO⊥平面ABCD；（2）设∠BAD=60°，AB=SD=2，P是侧棱SD上的一点，且SB∥平面APC，求三棱锥A﹣PCD 的体积．文科立体几何大题训练参考答案与试题解析一．解答题（共8小题）1．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．【解答】（1）证明：四棱锥P﹣ABCD中，∵∠BAD=∠ABC=90°．∴BC∥AD，∵AD⊂平面PAD，BC⊄平面PAD，∴直线BC∥平面PAD；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．设AD=2x，则AB=BC=x，CD=，O是AD的中点，连接PO，OC，CD的中点为：E，连接OE，则OE=，PO=，PE==，△PCD面积为2，可得：=2，即：，解得x=2，PO=2．则V P﹣ABCD=×（BC+AD）×AB×PO==4．2．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．【解答】解：（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC=B，可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；（2）证明：由AB=BC，D为线段AC的中点，可得BD⊥AC，由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面PAC∩平面ABC=AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD⊂平面BDE，可得平面BDE⊥平面PAC；（3）PA∥平面BDE，PA⊂平面PAC，且平面PAC∩平面BDE=DE，可得PA∥DE，又D为AC的中点，可得E为PC的中点，且DE=PA=1，由PA⊥平面ABC，可得DE⊥平面ABC，可得S△BDC=S△ABC=××2×2=1，则三棱锥E﹣BCD的体积为DE•S△BDC=×1×1=．3．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（Ⅰ）证明MN∥平面PAB；（Ⅱ）求四面体N﹣BCM的体积．【解答】证明：（Ⅰ）取BC中点E，连结EN，EM，∵N为PC的中点，∴NE是△PBC的中位线∴NE∥PB，又∵AD∥BC，∴BE∥AD，∵AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，∴BE=BC=AM=2，∴四边形ABEM是平行四边形，∴EM∥AB，∴平面NEM∥平面PAB，∵MN⊂平面NEM，∴MN∥平面PAB．解：（Ⅱ）取AC中点F，连结NF，∵NF是△PAC的中位线，∴NF∥PA，NF==2，又∵PA⊥面ABCD，∴NF⊥面ABCD，如图，延长BC至G，使得CG=AM，连结GM，∵AM CG，∴四边形AGCM是平行四边形，∴AC=MG=3，又∵ME=3，EC=CG=2，∴△MEG的高h=，∴S△BCM===2，∴四面体N﹣BCM的体积V N﹣BCM===．4．如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．（1）求证：DE∥平面PBC；（2）求证：AB⊥PE；（3）求三棱锥P﹣BEC的体积．【解答】证明：（1）∵D，E分别为AB，AC的中点，∴DE∥BC，又DE⊄平面PBC，BC⊂平面PBC，∴DE∥平面PBC．（2）连接PD，∵DE∥BC，又∠ABC=90°，∴DE⊥AB，又PA=PB，D为AB中点，∴PD⊥AB，又PD∩DE=D，PD⊂平面PDE，DE⊂平面PDE，∴AB⊥平面PDE，又PE⊂平面PDE，∴AB⊥PE．（3）∵平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，PD⊥AB，PD⊂平面PAB，∴PD⊥平面ABC，∵△PAB是边长为2的等边三角形，∴PD=，∵E是AC的中点，∴．5．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，PA=AB=2，E为PA 的中点，∠BAD=60°．（Ⅰ）求证：PC∥平面EBD；（Ⅱ）求三棱锥P﹣EDC的体积．【解答】（Ⅰ）证明：连接AC，BD，设AC与BD相交于点O，连接OE．由题意知，底面ABCD是菱形，则O为AC的中点，又E为AP的中点，∴OE∥CP，∵OE⊂平面BDE，PC⊄平面BDE，∴PC∥平面BDE；（Ⅱ）解：∵E为PA的中点，∴，∵四边形ABCD是菱形，∴AC⊥BD，又∵PA⊥平面ABCD，∴PA⊥BD，又PA∩AC=A，∴DO⊥平面PAC，即DO是三棱锥D﹣PCE的高，DO=1，则．6．如图，在三棱锥D﹣ABC中，DA=DB=DC，E为AC上的一点，DE⊥平面ABC，F为AB的中点．（Ⅰ）求证：平面ABD⊥平面DEF；（Ⅱ）若AD⊥DC，AC=4，∠BAC=45°，求四面体F﹣DBC的体积．【解答】证明：（Ⅰ）∵DE⊥平面ABC，AB⊂平面ABC，∴AB⊥DE，又F为AB的中点，DA=DB，∴AB⊥DF，DE，DF⊂平面DEF，DE∩DF=D，∴AB⊥平面DEF，又∵AB⊂平面ABD，∴平面ABD⊥平面DEF．（Ⅱ）∵DA=DB=DC，E为AC上的一点，DE⊥平面ABC，∴线段DA、DB、DC在平面ABC的投影EA，EB，EC满足EA=EB=EC∴△ABC为直角三角形，即AB⊥BC由AD⊥DC，AC=4，∠BAC=45°，∴AB=BC=2，DE=2，∴S△FBC==2，∴四面体F﹣DBC的体积V F﹣DBC=V D﹣FBC==．7．如图，四边形ABCD是正方形，平面ABCD⊥平面ABE，AF∥BE，AB⊥BE，AB=BE=2，AF=1．（Ⅰ）求证：AC⊥平面BDE；（Ⅱ）求证：AC∥平面DEF；（III）求三棱锥D﹣FEB的体积．【解答】（Ⅰ）证明：∵四边形ABCD是正方形，∴AC⊥BD．又∵平面ABEF⊥平面ABCD，平面ABEF∩平面ABCD=AB，AB⊥BE，BE⊂平面ABEF，∴BE⊥平面ABCD．又∵AC⊂平面ABCD．∴BE⊥AC，又BE∩BD=B，∴AC⊥平面BDE；（Ⅱ）证明：取DE的中点G，连结OG，FG，∵四边形ABCD为正方形，∴O为BD的中点．则OG∥BE，且．由已知AF∥BE，且，则AF∥OG且AF=OG，∴四边形AOGF为平行四边形，则AO∥FG，即AC∥FG．∵AC⊄平面DEF，FG⊂平面DEF，∴AC∥平面DEF；（Ⅲ）解：∵平面ABCD⊥平面ABEF，四边形ABCD是正方形，平面ABEF∩平面ABCD=AB，∴AD∥BC，AD⊥AB．由（Ⅰ）知，BE⊥平面ABCD，AD⊂平面ABCD，∴BE⊥AD∴AD⊥平面BEF．∴．8．如图，四棱锥S﹣ABCD中，底面ABCD是菱形，其对角线的交点为O，且SA=SC，SA⊥BD．（1）求证：SO⊥平面ABCD；（2）设∠BAD=60°，AB=SD=2，P是侧棱SD上的一点，且SB∥平面APC，求三棱锥A﹣PCD 的体积．【解答】解：（1）证明：∵底面ABCD是菱形；∴对角线BD⊥AC；又BD⊥SA，SA∩AC=A；∴BD⊥平面SAC，SO⊂平面SAC；∴BD⊥SO，即SO⊥BD；又SA=SC，O为AC中点；∴SO⊥AC，AC∩BD=O；∴SO⊥平面ABCD；（2）如图，连接PO；∵SB∥平面APC，SB⊂平面SBD，平面SBD∩平面APC=PO；∴SB∥PO；在△SBD中，O是BD的中点，PO∥SB，∴P是SD的中点；取DO中点，并连接PE，则PE∥SO，SO⊥底面ACD；∴PE⊥底面ACD，且PE=；根据已知条件，Rt△ADO中AD=2，∠DAO=30°，∴DO=1；∴在Rt△SDO中，SD=2，SO=；∴；又；∴V三棱锥A﹣PCD=V三棱锥P﹣ACD=．。

1.如图，正方体1111ABCD A B C D -的棱长为1，E 为线段1B C 上的一点，则三棱锥1A DED -的体积为＿＿＿＿＿.2.若四面体ABCD 的三组对棱分别相等，即AB CD =，AC BD =，AD BC =，则______(写出所有正确结论编号)。

①四面体ABCD 每组对棱相互垂直②四面体ABCD 每个面的面积相等③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90。

而小于180。

④连接四面体ABCD 每组对棱中点的线段互垂直平分⑤从四面体ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长3.α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线,给出四个论断：① m ⊥ n ②α⊥β ③ m ⊥β ④ n ⊥α以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：______________________________________.4.若直线a 不平行于平面α，则下列结论成立的是（ ）A. α内所有的直线都与a 异面；B. α内不存在与a 平行的直线；C. α内所有的直线都与a 相交；D.直线a 与平面α有公共点.5.直线a,b,c 及平面α,β,γ,下列命题正确的是（ ）A 、若a ⊂α，b ⊂α,c ⊥a, c ⊥b 则c ⊥αB 、若b ⊂α, a//b 则 a//αC 、若a//α,α∩β=b 则a//bD 、若a ⊥α, b ⊥α 则a//b6. 已知点P ，A ，B ，C ，D 是球O 表面上的点，PA ⊥平面ABCD ，四边形ABCD 是边长为正方形。

若则△OAB 的面积为______________.7. 如图，长方体1111D C B A ABCD -中，底面1111D C B A 是正方形，O 是BD 的中点，E 是棱1AA 上任意一点。

（Ⅰ）证明：BD 1EC ⊥ ；（Ⅱ）如果AB =2，AE =2，1EC OE ⊥,，求1AA 的长。

专题09 立体几何1.【2019年高考全国Ⅱ卷文数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面 【答案】B【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,a b a b αβ⊂⊂∥，则αβ∥”此类的错误．2．【2019年高考全国Ⅲ卷文数】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则（）A ．BM =EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知3,12EO ON EN ===,，35,,722MF BF BM ==∴=，BM EN ∴≠，故选B ．【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．3．【2019年高考江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD的体积是 ▲ .【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120，所以1120AB BC CC ⋅⋅=，因为E 为1CC 的中点，所以112CE CC =，由长方体的性质知1CC ⊥底面ABCD ，所以CE 是三棱锥E BCD -的底面BCD 上的高，所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=. 【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中，往往需要注意理清整体和局部的关系，灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.4．【2019年高考全国Ⅱ卷文数】如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，AB =3，求四棱锥11E BB C C -的体积． 【答案】（1）见详解；（2）18.【解析】（1）由已知得B 1C 1⊥平面ABB 1A 1，BE ⊂平面ABB 1A 1，故11B C BE ⊥．又1BE EC ⊥，所以BE ⊥平面11EB C ． （2）由（1）知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E ， 所以1145AEB A EB ︒∠=∠=，故AE =AB =3，126AA AE ==.作1EF BB ⊥，垂足为F ，则EF ⊥平面11BB C C ，且3EF AB ==． 所以，四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=． 【名师点睛】本题主要考查线面垂直的判定，以及四棱锥的体积的求解，熟记线面垂直的判定定理，以及四棱锥的体积公式即可，属于基础题型.一、考向分析：二、考向讲解考查内容解 题 技 巧 几何 体表 面积 与体 积1、空间几何体表面积的求法（1）以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量。

立体几何（文科)1、如图1。

4所示四棱锥P。

ABCD中，底面是以O为中心的菱形,PO⊥底面ABCD,AB＝2,∠BAD＝错误!，M为BC上一点，且BM＝错误!.(1）证明：BC⊥平面POM;(2）若MP⊥AP，求四棱锥P。

ABMO的体积．516图42、四面体ABCD及其三视图如图1­4所示，平行于棱AD，BC的平面分别交四面体的棱AB，BD，DC，CA于点E,F，G，H。

图1。

4（1）求四面体ABCD的体积；错误!.(2）证明：四边形EFGH是矩形．3、如图1。

5，在三棱柱ABC .A1B1C1中，侧棱垂直于底面,AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A1C1，BC的中点．图1。

5（1）求证：平面ABE⊥平面B1BCC1；(2）求证：C1F∥平面ABE；(3)求三棱锥E。

ABC的体积．错误!.4、如图1.3，四棱锥P。

ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．（1）证明：PB∥平面AEC；(2）设AP＝1，AD＝错误!，三棱锥P­ABD的体积V＝错误!，求A到平面PBC的距离．错误!图1­3。

5、如图1­6所示,三棱锥A . BCD 中，AB ⊥平面BCD ，CD ⊥BD 。

（1）求证：CD ⊥平面ABD ；(2）若AB ＝BD ＝CD ＝1,M 为AD 中点，求三棱锥A ­ MBC 的体积．错误!图1。

66、如图1。

4所示，△ABC 和△BCD 所在平面互相垂直，且AB ＝BC ＝BD ＝2，∠ABC ＝∠DBC ＝120°,E ，F ，G 分别为AC ，DC ,AD 的中点．（1）求证：EF ⊥平面BCG ；(2)求三棱锥D 。

BCG 的体积．错误!。

7、如图， 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心， A 1O ⊥平面ABCD, 1AB AA ==1A（Ⅰ) 证明: A 1BD // 平面CD 1B 1； (Ⅱ） 求三棱柱ABD -A 1B 1D 1的体积.8、如图,在四棱锥P ABCD -中,PD ABCD ⊥面,//AB DC ，AB AD ⊥,5BC =,3DC =，4AD =，60PAD ∠=。