人教课标版高中数学选修2-3《回归分析》参考学案

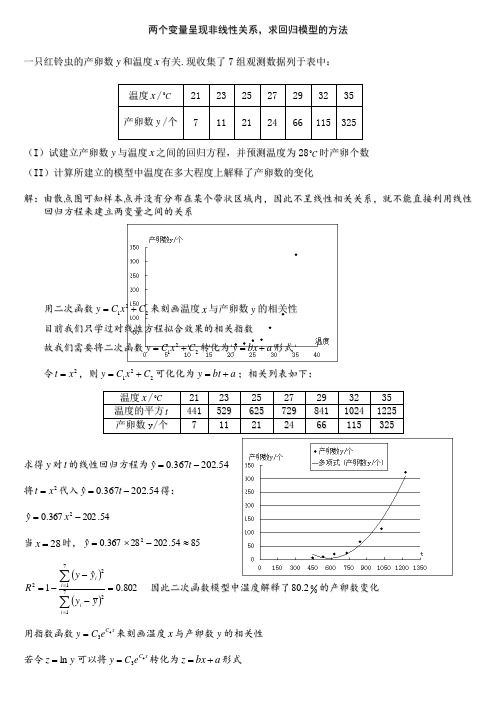
两个变量呈现非线性关系，求回归模型的方法一只红铃虫的产卵数y 和温度x 有关.现收集了7组观测数据列于表中：（I ）试建立产卵数y 与温度x 之间的回归方程，并预测温度为28C 0时产卵个数（I I ）计算所建立的模型中温度在多大程度上解释了产卵数的变化解：由散点图可知样本点并没有分布在某个带状区域内，因此不呈线性相关关系，就不能直接利用线性 回归方程来建立两变量之间的关系用二次函数221C x C y +=来刻画温度x 与产卵数y 的相关性 目前我们只学过对线性方程拟合效果的相关指数故我们需要将二次函数221C x C y +=转化为a bx y +=形式 令2x t =，则221C x C y +=可化化为a bt y +=；相关列表如下：求得y 对t 的线性回归方程为54.202367.0ˆ-=t y 将2x t =代入54.202367.0ˆ-=t y得： 54.202367.0ˆ2-=x y当28=x 时，8554.20228367.0ˆ2≈-⨯=y()()802.0ˆ17127122=---=∑∑==i i i i y y y y R 因此二次函数模型中温度解释了002.80的产卵数变化用指数函数x C e C y 43=来刻画温度x 与产卵数y 的相关性 若令y z ln =可以将x C e C y 43=转化为a bx z +=形式温度x /C 02123 25 27 293235产卵数y /个 7 11212466 115 325温度x /C 0 21 23 2527 29 32 35 温度的平方t 441 529 625 729 841 1024 1225 产卵数y /个7 11212466 115 325对x C e C y 43=两边取对数343ln ln ln ln 4C x C e C y x C +=+=令y z ln =，b C =4，a C =3ln 则有a bx z +=；相关列表如下：求得z 对x 的线性回归方程为849.3272.0ˆ-=x z将272.04=C ，849.3-3e C =代入x C e C y 43=得：849.3272.0ˆ-=x e y当28=x 时，44ˆ849.328272.0≈=-⨯e y利用计算器求得98.02=R因此二次函数模型中温度解释了0098的产卵数变化综上可得用指数模型拟合效果较好，也就是说刻画产卵数与温度的关系更接近实际情况1.在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是( ) A .总偏差平方和 B .残差平方和 C .回归平方和 D .相关指数R 22.回归分析中，相关指数R 2的值越大，说明残差平方和( )A .越小B .越大C .可能大也可能小D .以上都不对3.若对于变量y 与x 的10组统计数据的回归模型中，相关指数95.02=R ，又知残差平方和为53.120，那么∑=-1012)(i i y y 的值为（ ） （A ) 06.241 （B ）6.2410 （C ）08.253 （D ）8.25304.在一次抽样调查中测得样本的5个样本点，数据如下： （1）画出散点图；（2）通过作出的散点图发现，y 与x 之间的关系可用函数a xby +=拟合，试确定a b ,的值 温度x /C 021232527293235y z ln = 1.946 2.398 3.405 3.178 4.19 4.745 5.784 产卵数y /个 7 11 21 24 66 115 325 x 0.25 0.5 1 2 4 y 16 125 2 1。

第二课时教学目标知识与技能从相关指数和残差分析角度探讨回归模型的拟合效果，以及建立回归模型的基本步骤．过程与方法在发现直接求回归直线方程存在缺陷的基础上，引导学生去发现解决问题的新思路——进行回归分析，进而介绍残差分析的方法和利用R2来表示解释变量对于预报变量变化的贡献率．情感、态度与价值观通过本节课的学习，加强数学与现实生活的联系，以科学的态度评价两个变量的相关性，掌握处理问题的方法，形成严谨的治学态度和锲而不舍的求学精神．培养学生运用所学知识解决实际问题的能力．教学中适当地利用学生的合作与交流，使学生在学习的同时，体会与他人合作的重要性．重点难点教学重点：从残差分析、相关指数角度探讨回归模型的拟合效果，以及建立回归模型的基本步骤；教学难点：了解评价回归效果的两个统计量：相关指数、残差和残差平方和．教学过程引入新课上表是上一节课我们从某大学选取8名女大学生其身高和体重数据组成的数据表，在上一节课中我们通过数据建立了回归直线方程，并根据方程预测了身高为172 cm的女大学生的体重．当时，我们提到根据回归直线方程求得的体重数据，仅是一个估计值，其与真实值之间存在着误差，为了综合分析身高和体重的关系，我们引入了线性回归模型y＝bx＋a＋e 来表示两变量之间的关系，其中e为随机变量，又称随机误差．线性回归模型y＝bx＋a＋e 增加了随机误差项e，因变量y的值由自变量x和随机误差e共同确定．假设随机误差对体重没有影响，也就是说，体重仅受身高的影响，那么散点图中所有的点将完全落在回归直线上．但是，在图中，数据点并没有完全落在回归直线上．这些点散布在回归直线附近，所以一定是随机误差把这些点从回归直线上“推”开了，即自变量x只能解释部分y的变化．同学们考虑一下，随机变量e的均值是多少？方差又是多少？活动设计：学生思考回答问题．学情预测：学生回答E(e)＝0，D(e)＝σ2>0.教师提问：能否通过D(e)来刻画线性回归模型的拟合程度？学情预测：随机误差e的方差越小，通过回归直线预报真实值y的精度越高．随机误差是引起预报值与真实值y之间的误差的原因之一，其大小取决于随机误差的方差．设计意图：说明研究随机误差e的必要性，通过研究随机误差e可以分析预报值的可信度．提出问题：既然可以用随机变量e的方差来衡量随机误差的大小，即通过方差σ2来刻画预报变量(体重)的变化在多大程度上与随机误差有关，那么如何获得方差σ2呢？学生活动：学生独立思考，小组合作交流讨论．活动结果：可以采用抽样统计的思想，通过随机变量e的样本来估计σ2的大小．设计目的：复习抽样统计思想，以便通过随机变量e 的样本来估计总体． 探究新知提出问题：既然e 表示了除解释变量以外其他各种影响预报值的因素带来的误差，那么如何获得e 的样本来计算σ2呢？学生活动：分组合作讨论交流．学情预测：由函数模型y ^＝b ^x ＋a ^和回归模型y ＝bx ＋a ＋e 可知e ＝y －y ^，这样根据图表中女大学生的身高求出预报值，再与真实值作差，即可求得e 的一个估计值．教师：由于在计算回归直线方程时，利用公式求得的b ^和a ^为斜率和截距的估计值，它们与真实值a 和b 之间存在误差，因此y ^是估计值，所以e ^＝y －y ^也是一个估计值．由上可知，对于样本点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )而言，它们的随机误差为e i ＝y i －bx i －a ，i ＝1,2，…n ，称其估计值e ^i ＝y i －y ^i 为相应于点(x i ，y i )的残差．将所有残差的平方加起来，即∑i ＝1ne ^2i ，这个和称作残差平方和．类比样本方差估计总体方差的思想，可以用σ^2＝1n －2∑i ＝1n e ^ 2i ＝1n －2∑i ＝1n(y i －y ^i )2(n>2) 作为σ2的估计量，通常，σ^2越小，预报精度越高．这样，当我们求得回归直线方程后，可以通过残差来判断模型拟合程度的效果，判断原始数据中是否存在可疑数据，这方面的分析工作称为残差分析．设计目的：通过问题诱思，引入残差概念． 理解新知提出问题：对照女大学生的身高和体重的原始数据，结合求出的回归直线方程，求出相应的残差数据．学生活动：独立完成．样的散点图称作残差图)．学生活动：分组合作，共同完成． 活动结果：残差图提出问题：观察上面的残差图，你认为哪几个样本点在采集时可能存在人为的错误？为什么？学生活动：分组讨论． 活动结果：第一个和第六个样本点在采集过程中可能存在错误，因为其他的样本点基本都集中在一个区域内，只有这两个样本点的残差比较大，相对其他样本点来说，分布得较为分散．提出问题：如何从残差图来判断模型的拟合程度？ 学生活动：独立思考也可相互讨论．活动结果：因为σ^2越小，预报精度越高，即模型的拟合程度越高，而σ^2越小，e ^的取值越集中，故若残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适，且带状区域的宽度越窄，说明拟合精度越高，回归直线的预报精度越高．教师：在统计学上，人们经常用相关指数R 2来刻画回归的效果，其计算公式是：R 2＝1－∑i ＝1n(y i －y ^i )2∑i ＝1n(y i －y )2提出问题：分析上面计算相关指数R 2的公式，如何根据R 2来判断模型的拟合效果？ 学生活动：独立思考也可相互讨论，教师加以适当的引导提示．活动结果：因为对于确定的样本数据而言，∑i ＝1n(y i －y )2是一个定值，故R 2取值越大，意味着残差平方和越小，也就是说模型的拟合效果越好．提出问题：在线性回归模型中，R 2表示解释变量对于预报变量变化的贡献率，R 2越接近1，表示回归的效果越好，即解释变量和预报变量的线性相关性越强，试计算关于女大学生身高与体重问题中的相关指数R 2.学生活动：学生独立计算获得数据． 活动结果：R 2≈0.64.根据R 2≈0.64就可得出“女大学生的身高解释了64%的体重变化”，或者说“女大学生的体重差异有64%是由身高引起的”．由此就不难理解为什么预报体重和真实值之间有差距了．设计目的：结合图象，让学生直观感受残差图在刻画回归模型拟合效果方面的应用，体会残差分析和相关指数的意义．提出问题：根据前面得到的回归方程，能否预测一名美国女大学生的体重？建立回归模型后能否一劳永逸，在若干年后还可以使用，或者适用于多年以前的女大学生体重预测？学生活动：讨论交流总结发言．活动结果：在使用回归方程进行预报时要注意： (1)回归方程只适用于我们所研究的样本的总体； (2)我们建立的回归方程一般都有时间性；(3)样本取值的范围会影响回归方程的适用范围；(4)不能期望回归方程得到的预报值就是预报变量的精确值．提出问题：结合我们刚学习的概念，现在能否将建立回归模型的步骤补充完整？ 学生活动：讨论交流，合作完成．活动结果：一般地，建立回归模型的基本步骤为：(1)确定研究对象，明确哪个变量是解释变量，哪个变量是预报变量．(2)画出确定好的解释变量和预报变量的散点图，观察它们之间的关系(如是否存在线性关系等)．(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系，则选用线性回归方程)． (4)按一定规则(如最小二乘法)估计回归方程中的参数．(5)得出结果后分析残差图是否有异常(如个别数据对应残差过大，或残差呈现不随机的规律性，等等)．若存在异常，则检查数据是否有误，或模型是否合适等．设计意图：设计问题，让学生讨论分析，得出使用回归方程进行预报需注意的问题，并让学生完善建立回归模型的步骤．在这个过程中，教师不宜做太多引导，要放手给学生，让学生讨论，充分参与进来．运用新知例1一个车间为了规定工时定额，需确定加工零件所花费的时间，为此进行了10次试(1)建立零件数为解释变量，加工时间为预报变量的回归模型，并计算残差； (2)你认为这个模型能较好地刻画零件数和加工时间的关系吗？ 分析：首先根据散点图粗略判断变量是否具有线性相关性，判断是否可以用线性回归模型来拟合数据，然后通过残差e ^1，e ^2，…，e ^n 来判断模型拟合的效果，判断原始数据是否存在可疑数据．解：(1)根据表中数据作出散点图如下：散点图由散点图可知变量之间具有线性相关关系，可以通过求线性回归方程来拟合数据．根据公式可求得加工时间对零件数的线性回归方程为y ^＝0.668x ＋54.96.残差数据如下表：残差图由图可知，残差点分布较均匀，即用上述回归模型拟合数据效果很好，但需注意，由残差图也可以看出，第4个样本点和第5个样本点残差较大，需要确认在采集这两个样本点的过程中是否有人为的错误．点评：由散点图判断两个变量的线性相关关系，误差较大，利用残差图可以较好地评价模型的拟合程度，并能发现样本点中的可疑数据．【变练演编】例2求出y 对x 的回归方程，并说明拟合效果的好坏．思路分析：先根据散点图判断两个变量是否线性相关，若相关，求出回归直线方程，然后通过相关指数的大小来评价拟合效果的好坏．解：作出散点图：从作出的散点图可以看出，这些点在一条直线附近，可用线性回归模型来拟合数据．由数据可得x ＝18，y ＝45.4，由计算公式得b ^＝－2.35，a ^＝y －b ^x ＝87.7.故y 对x 的回归方程为y ^＝－2.35x ＋87.7，列表：所以∑i ＝15(y i －y ^i )2＝8.3，∑i ＝15(y i －y )2＝229.2.相关指数R 2＝1－∑i ＝15(y i －y ^i )2∑i ＝15(y i －y )2≈0.946.因为0.964很接近1，所以该模型的拟合效果很好．变式1：若要分析是否在上述样本的采集过程中存在可疑数据，应如何分析？ 活动设计：学生分组讨论，回顾课本解答问题． 活动成果：可以画出残差图来进行分析．变式2：既然利用残差图和相关指数都能够评价回归模型的拟合效果，能否总结一下两种方法各自的特点？活动成果：利用残差图可以直观展示拟合的效果，而且还可以发现样本数据中的可疑数据；而相关指数是把对拟合效果的评价转换为数值大小的判断，易于量化处理，并能在数量上表现解释变量对于预报变量变化的贡献率．设计意图：进一步熟悉判断拟合效果的方法以及各自的特点． 【达标检测】1．分析下列残差图，所选用的回归模型效果最好的是()ABC D 2．下列说法正确的是( )①回归直线方程适用于一切样本和总体；②回归直线方程一般都有时间性；③样本的取值范围会影响回归直线方程的适用范围；④根据回归直线方程得到的预测值是预测变量的精确值．A ．①③④B ．②③C ．①②D ．③④3．在研究气温和热茶销售杯数的关系时，若求得相关指数R 2≈__________，表明“气温解释了85%的热茶销售杯数变化”或者说“热茶销售杯数差异有85%是由气温引起的”．答案：1.D 2.B 3.0.85.课堂小结学生回顾本节课学习的内容，尝试总结，然后不充分的地方由学生相互补充，最后在老师的引导下，用精炼的语言进行概括：1．判断变量是否线性相关的方法以及各自的特点； 2．在运用回归模型时需注意的事项； 3．建立回归模型的基本步骤． 设计意图：让学生自己小结，这是一个多维整合的过程，是一个高层次的自我认识过程． 补充练习 【基础练习】1．有下列说法：①在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适．②用相关指数R 2来刻画回归的效果，R 2值越接近于1，说明模型的拟合效果越好．③比较两个模型的拟合效果，可以比较残差平方和的大小，残差平方和越小的模型，拟合效果越好．正确的是( )A ．①②B ．②③C ．①③D ．①②③2．甲、乙、丙、丁四位同学各自对A ，B 两变量做回归分析，分别得到散点图与残差平方和∑i ＝1n(y i －y ^i )2如下表115106124103哪位同学的实验结果体现拟合A ，B 两变量关系的模型拟合精度高？( ) A ．甲 B ．乙 C ．丙D ．丁 3．关于x 与y 为了对x ，y 两个变量进行统计分析，现有以下两种线性模型：甲：y ^＝6.6x ＋17.5，乙：y ^＝7x ＋17.试比较哪一个模型拟合效果更好．答案或提示：1.D 2.D3．解析：设甲模型的相关指数为R 21，则R 21＝1－∑i ＝15(y i －y ^i )2∑i ＝15(y i －y )2＝1－1551 000＝0.845；设乙模型的相关指数为R 22，则可求得R 22＝0.82，因为R 21>R 22，所以甲模型的拟合效果更好．【拓展练习】 4．假设某种农作物基本苗数x 与有效穗数y 之间存在相关关系，今测得5组数据如下：(1)以x 为解释变量，y 为预报变量，作出散点图；(2)求y 与x 之间的回归方程，对于基本苗数56.7预报有效穗数． (3)计算各组残差；(4)求R 2，并说明随机误差对有效穗数的影响占百分之几？ 解：(1)散点图如图：(2)由图可以看出，样本点呈条状分布，有比较好的线性相关关系，因此可用线性回归方程来建立两个变量之间的关系．设线性回归方程为y ^＝b ^x ＋a ^，由数据可以求得：b ^≈0.291，a ^＝y －b ^x ＝34.67.故所求的线性回归方程为y ^＝0.291x ＋34.67.当x ＝56.7时，y ^＝0.291×56.7＋34.67＝51.169 7. 估计有效穗数为51.169 7.(3)各组数据的残差分别是e ^1≈0.37，e ^2≈0.72，e ^3≈－0.5，e ^4≈－2.22，e ^5≈1.61. (4)残差平方和：∑i ＝15(y i －y ^i )2＝8.425 8，又∑i ＝15(y i －y )2＝50.18，∴R 2＝1－∑i ＝15(y i －y ^i )2∑i ＝15 (y i －y )2＝1－8.425 850.18≈0.832.即解释变量(农作物基本苗数)对有效穗数的影响约占了83.2%，所以随机误差对有效穗数的影响约占1－83.2%＝16.8%.设计说明 本课时从上一节课的案例出发，通过分析随机误差产生的原因，引入随机变量、残差、残差平方和、相关指数的有关概念，从相关指数和残差分析等角度探讨回归模型拟合的效果，并通过案例说明利用所建立的回归模型进行预报时需要注意的问题，然后总结建立回归模型的基本步骤．在教学过程中以问题为引导思考的动机，注重对学生合作意识的培养，通过对案例的分析，培养学生对数据的处理能力，让学生初步了解回归分析思想在实际生活中的运用．备课资料有关总偏差平方和、回归平方和、残差平方和以及相关指数等概念的说明 1．总偏差平方和：SST ＝∑i ＝1n(y i －y )2，刻画了预报变量y 的变化剧烈程度．2．回归平方和：SSR ＝∑i ＝1n(y ^i －y )2，公式中所有预测值的平均值也等于y ，故1n ∑i ＝1n y ^ i ＝1n ∑i ＝1n (b ^x i ＋a ^ )＝b ^ x ＋a ^ ＝b ^ x ＋y －b ^x ＝y ， 因此回归平方和又可以写成.从而回归平方和刻画了估计量y ^＝a ^＋b ^x 的变化程度．由于估计量由解释变量x 所决定，所以，回归平方和刻画了预报变量的变化中由解释变量通过线性回归模型引起的那一部分的变化程度．3．残差平方和：SSE ＝∑i ＝1n(y i －y ^i )2，刻画了残差变量变化的程度．4．偏差平方和分解：即指公式∑i ＝1n(y i －y )2＝∑i ＝1n(y ^i －y )2＋∑i ＝1n(y i －y ^i )2，称为平方和分解公式，用文字表示为： 总偏差平方和＝回归平方和＋残差平方和． 公式证明如下：假设观测数据为(x i ，y i )，i ＝1,2，…，n ，则∑i ＝1n(y i －y )2＝∑i ＝1n(y i －y ^i ＋y ^i －y )2＝∑i ＝1n(y i －y )2＋∑i ＝1n(y i －y ^i )2＋2∑i ＝1n(y ^ i －y )(y i －y ^i )．而∑i ＝1n(y ^ i －y )(y i －y ^i )＝∑i ＝1n(b ^ x i －b ^ x )(y i －a ^ －b ^x i )＝∑i ＝1nb ^(x i －x )[]y i －a ^ －b ^x －b(x i －x )＝b ^∑i ＝1n(x i －x )[](y i －y )－b ^(x i －x )＝b ^⎣⎢⎢⎡⎦⎥⎥⎤∑i ＝1n (x i－x )(y i －y )－b ^ ∑i ＝1n (x i －x )2＝0， 代入上式即可证得平方和分解公式． 这样，可以把平方和分解公式解释为：预报变量的变化程度可以分解为由解释变量引起的变化程度与残差变量引起的变化程度之和．由平方和分解公式得1＝∑i ＝1n(y ^i －y )2∑i ＝1n(y i －y )2＋∑i ＝1n(y i －y ^i )2∑i ＝1n(y i －y )2这意味着在线性回归模型中，预报变量的1个单位的变化，需要由解释变量贡献∑i ＝1n(y ^i －y )2∑i ＝1n(y i －y )2，由残差变量贡献∑i ＝1n(y i －y ^i )2∑i ＝1n(y i －y )2，因此在线性回归模型中，我们说预报变量y的变化中的100×∑i ＝1n(y ^i －y )2∑i ＝1n(y i －y )2%是由解释变量x 所引起的，或者说解释变量x 可以解释预报变量y 的100×∑i ＝1n(y ^i －y )2∑i ＝1n(y i －y )2%的变化．又∑i ＝1n(y ^i －y )2∑i ＝1n(y i －y )2＝1－∑i ＝1n(y i －y ^i )2∑i ＝1n(y i －y )2＝R 2，即R 2＝∑i ＝1n(y ^i －y )2∑i ＝1n(y i －y )2，这说明“预报变量y 的变化中的百分之100R 2是由解释变量x 所引起的，或者说解释变量x 可以解释预报变量y 的百分之100R 2的变化．因此，R 2越大拟合效果越好，反之越小．(设计者：杨雪峰)。

§3.1 回归分析的基本思想及其初步应用教学目标知识与技能能根据散点分布特点，建立不同的回归模型；知道有些非线性模型通过变换可以转化为线性回归模型；通过散点图及相关指数比较不同模型的拟合效果．过程与方法通过将非线性模型转化为线性回归模型，使学生体会“转化”的思想；让学生经历数据处理的过程，培养他们对数据的直观感觉，体会统计方法的特点，认识统计方法的应用；通过使用转化后的数据，利用计算器求相关指数，使学生体会使用计算器处理数据的方法．情感、态度与价值观通过案例的解决，开阔学生的思路，培养学生的探索精神和转化能力，并通过合作学习，培养学生的团队合作意识．重点难点教学重点：通过探究使学生体会有些非线性模型运用等量变换、对数变换可以转化为线性回归模型；教学难点：如何启发学生“对变量作适当的变换(等量变换、对数变换)”，变非线性为线性，建立线性回归模型．教学过程引入背景材料我国是世界产棉大国，种植棉花是我国很多地区农民的主要经济来源，在棉花的种植过程中，病虫害的防治是棉农的一项重要任务，如果处置不当就会造成棉花的减产．其中红铃虫就是危害棉花生长的一种常见害虫，在1953年，我国18省曾发生红铃虫大灾害，受灾面积300万公顷，损失皮棉约二十万吨．如图就是红铃虫的有关图片：红铃虫喜高温高湿，适宜各虫态发育的温度为25～32 ℃，相对湿度为80%～100%，低于20 ℃和高于35 ℃卵不能孵化，相对湿度60%以下成虫不产卵．冬季月平均气温低于－4.8 ℃时，红铃虫就不能越冬而被冻死．为采取有效防治方法，有必要研究红铃虫的产卵数和温度之间的关系．现收集了红铃虫的产卵数y和温度x之间的7组观测数据列于下表：温度x/℃21 23 25 27 29 32 35产卵数y/个7 11 21 24 66 115 325(1)试建立y与x之间的回归方程；并预测温度为28 ℃时产卵的数目．(2)你所建立的模型中温度在多大程度上解释了产卵数的变化？学生活动：类比前面所学过的建立线性回归模型的步骤，动手实施．活动结果：(1)画散点图：通过计算器求得线性回归方程：y ^＝19.87x －463.73.当x ＝28 ℃时，y ^＝19.87×28－463.73≈93，即温度为28 ℃时，产卵数大约为93. (2)进行回归分析计算得： R 2≈0.746 4，即这个线性回归模型中温度解释了74.64%产卵数的变化．设计目的：通过背景材料，加深学生对问题的理解，并明白“为什么要学”．体会问题产生于生活，并通过问题的解决复习建立回归模型的基本步骤．探究新知提出问题：结合数据可以发现，随着自变量的增加，因变量也随之增加，气温为28 ℃时，估计产卵数应该低于66个，但是从推算的结果来看93个比66个却多了27个，是什么原因造成的呢？学生活动：分组合作讨论交流．学情预测：由于我们所建立的线性回归模型的相关指数约等于0.746 4，即解释变量仅能解释预报变量大约74.64%的变化，所占比例偏小．这样根据我们建立的模型进行预报，会存在较大的误差．我们还可以从残差图上分析一下我们所建立的回归模型的拟合效果：残差数据表： x 21 23 25 27 29 32 35 y 7 11 21 24 66 115 325 残差53.4617.72－12.02－48.78－46.5－57.1193.28画出残差图根据残差图可以发现，残差点分布的带状区域较宽，并不集中，这表明我们所建立的回归模型拟合效果并不理想．之所以造成预报值偏差太大的原因是所选模型并不理想．实际上根据散点图也可以发现，样本点并没有很好地集中在一条直线附近，故变量之间不会存在很强的线性相关性．设计目的：引导学生对结果进行分析，从而发现存在的问题，激发好奇心、求知欲．同时培养学生对问题的洞悉能力，增强对结果的敏感自检能力．理解新知提出问题：如何选择合适的回归模型进行预测呢？学生活动：学生讨论，教师合理引导学生观察图象特征，联想学过的基本函数． 学情预测：方案一：建立二次函数模型y ＝bx 2＋a . 方案二：建立指数函数模型y ＝c 1ac 2x .提出问题：如何求出所建立的回归模型的系数呢？我们不妨尝试解决方案一中的系数． 学生活动：分组合作，教师引导学生观察y ＝bx 2＋a 与y ＝bx ＋a 的关系．学情预测：通过比较，发现可利用t ＝x 2，将y ＝bx 2＋a (二次函数)转化成y ＝bt ＋a (一次函数)．求出x ，t ，y 间的数据转换表：x 21 23 25 27 29 32 35 t ＝x 2 441 529 625 729 841 1 024 1 225 y711212466115325利用计算器计算出y 和t 的线性回归方程：y ^＝0.367t －202.54，转换回y 和x 的模型：y ^＝0.367x 2－202.54.当x ＝28 ℃时，y ^＝0.367×282－202.54≈85，即温度为28 ℃时，产卵数大约为85. 计算相关指数R 2≈0.802，这个回归模型中温度解释了80.2%产卵数的变化． 提出问题：提出问题“如果选用指数模型，是否也能转换成线性模型，如何转化？” 学生活动：独立思考也可相互讨论．教师可启发学生思考“幂指数中的自变量如何转化为自变量的一次幂？”可引导学生回忆对数的运算性质以及指对数关系．学情预测：可利用取对数的方法，即在y ＝c 1ac 2x 两边取对数，得log a y ＝c 2x ＋log a c 1. 提出问题：在上面的运算中，由于底数a 不确定，对于x 的值无法求出相应的log a y ，这时可取a ＝10时的情况，以便利用计算器进行计算，试求出回归模型．学生活动：合作协作，讨论解决． 学情预测：建立数据转换表：x 21 23 25 27 29 32 35 z ＝lg y 0.85 1.04 1.32 1.38 1.82 2.06 2.51 y711212466115325根据数据，可求得变量z 关于x 的回归方程：z ^＝0.118x －1.665. 转换回y 和x 的模型：y ^＝100.118x－1.665.当x ＝28 ℃时，y ^≈44，即温度为28 ℃时，产卵数大约为44.计算相关指数R 2≈0.985，这个回归模型中温度解释了98.5%产卵数的变化．提出问题：试选择合适的方法，比较方案一和方案二在数据拟合程度上的效果有什么不同？学生活动：独立思考也可相互讨论，教师加以适当的引导提示． 活动结果：相关指数R 2残差平方和残差图方案一0.802 15 448.432方案二0.985 1 450.673无论从图形上直观观察，还是从数据上分析，指数函数模型都是更好的模型．设计目的：引导学生进行不同模型的比较，体会“虽然任意两个变量的观测数据都可以用线性回归模型来拟合，但不能保证这种模型对数据的拟合效果最好，为更好地刻画两个变量之间的关系，要根据观测数据的特点来选择回归模型”．提出问题：由上面的分析可以看出，回归模型不一定是线性回归模型，对于非线性回归模型，我们的处理方法是什么？学生活动：独立思考，回顾上面的解决过程．学情预测：选用非线性回归模型时，一般思路是转化成线性回归模型，往往要用“等量变换、对数变换”等方法．设计目的：让学生整理建立非线性回归模型的思路．运用新知例1为了研究某种细菌繁殖个数y与时间x的关系，收集数据如下：天数x(天) 1 2 3 4 5 6繁殖个数y(个) 6 12 25 49 95 190 试建立y与x之间的回归方程．解：根据上表中的数据，作出散点图由图可以看出，样本点分布在某指数函数曲线y ＝c 1ec 2x 的周围，于是令z ＝lny ，则上表变换后如下：x 1 2 3 4 5 6 z1.792.483.223.894.555.25作出散点图从图中可以看出，变换后的样本点分布在某条直线附近，因此可用线性回归模型来拟合． 由表中数据可得，z 与x 之间的线性回归方程为z ^＝0.69x ＋1.112， 则y 与x 之间的回归方程为y ^＝e 0.69x +1.112. 变练演编例2混凝土的抗压强度X 较易测定，其抗弯强度Y 不易测定，已知X 与Y 由关系式Y＝AX b 表示，工程中希望由X 估算出Y ，以便应用．现测得一批对应数据如下：X 141 152 168 182 195 204 223 254 277 Y23.125.325.929.831.131.832.534.835.2试求Y 对X 的回归方程．解：对Y ＝AX b 两边取自然对数得：ln Y ＝b ln X ＋ln A ，做变换y ＝ln Y ，x ＝ln X ，a ＝ln A ，则上述数据对应表格如下：X 141 152 168 182 195 204 223 254 277 Y 23.1 25.3 25.9 29.8 31.1 31.8 32.5 34.8 35.2 x 4.95 5.02 5.12 5.20 5.27 5.32 5.41 5.54 5.62 y3.143.233.253.393.443.463.483.553.56根据公式可求得y ^＝0.64x ＋0.017 2，则 Y ^＝e 0.64ln x＋0.017 2＝1.02X 0.64.变式1：若X 与Y 的关系由关系式Y ^＝β^X b ＋α^表示，试根据给出的数据求Y 对X 的回归方程．活动设计：学生分组讨论，尝试解决． 活动成果：Y ^＝0.086X ＋13.005.变式2：试选择合适的方法比较上述两种回归模型，相对于给出的数据哪一个的拟合效果更好？活动成果：计算残差平方和与相关指数，对于模型Y ＝AX b，残差平方和Q ^(1)＝9.819，相关指数R 21＝0.930 4；对于模型Y ^＝β^X b ＋α^，残差平方和Q ^(2)＝12.306，相关指数R 22＝0.908，故模型Y ＝AX b 的拟合效果较好．设计意图：熟悉判断回归模型拟合效果的方法． 达标检测1．变量x ，y 的散点图如图所示，那么x ，y 之间的样本相关系数r 最接近的值为( )A．1B．－0.5C．0 D．0.52．变量x与y之间的回归方程表示()A．x与y之间的函数关系B．x与y之间的不确定性关系C．x与y之间的真实关系形式D．x与y之间的真实关系达到最大限度的吻合3．非线性回归分析的解题思路是__________．【答案】1.C 2.D 3.通过变量置换转化为线性回归分析课堂小结1．数学知识：建立回归模型及残差图分析的基本步骤；非线性模型向线性模型的转换方法；不同模型拟合效果的比较方法：相关指数和残差的分析．2．数学思想：数形结合的思想，化归思想及整体思想．3．数学方法：数形结合法，转化法，换元法．补充练习基础练习1．相关指数R2，残差平方和与模型拟合效果之间的关系是()A．R2的值越大，残差的平方和越大，拟合效果越好B．R2的值越小，残差的平方和越大，拟合效果越好C．R2的值越大，残差的平方和越小，拟合效果越好D ．以上说法都不正确2．如果散点图的所有点都在一条直线上，则残差均为____________________，残差平方和为__________，相关指数为______________．【答案】1.C 2.0 0 1 拓展练习3．某种书每册的成本费Y 元与印刷册数x (千册)有关，经统计得到数据如下： x 1 2 3 5 10 20 30 50 100 200 Y10.155.524.082.852.111.621.411.301.211.15检验每册书的成本费Y 元与印刷册数的倒数1x 之间是否有线性相关关系，如有，求出Y对1x的回归方程． 解：把1x 置换为z ，则z ＝1x ，从而z 与Y 的数据为：z 1 0.5 0.333 0.2 0.1 0.05 0.033 0.02 0.01 0.005 Y10.155.524.082.852.111.621.411.301.211.15根据数据可得r ≈0.999 8>0.75，故z 与Y 具有很强的线性相关关系． 所以b ^≈8.976，a ^≈1.120，从而y ^＝8.976z ＋1.120.又z ＝1x ，所以y ^＝8.976x＋1.120.设计说明本课时内容教材中只安排了一道关于“红铃虫”的例题，但是它却代表了一种“回归分析”的类型．如何利用这道例题使学生掌握这类问题的解决方法呢？为此，本课时设计了“引导发现、合作探究”的教学方法．首先展示“红铃虫”的背景资料来激发学生的学习兴趣；鼓励学生用已有知识解决问题，引导学生检查结果从而发现新问题；通过分组合作来对不同方案进行探索；使学生在合作探索的过程中体会“选择模型——将非线性转化成线性”的方法，体会“化未知为已知、用已知探索未知”思想，同时认识不同模型的效果．培养学生观察、类比联想以及分析问题的能力．在教学过程中让学生自主探索、动手实践，养成独立思考、积极探索的习惯．在“选模型”这个环节中，注意引导学生将散点分布和已学函数图象进行比较，从而发现二次函数和指数函数模型．在“转化”这个环节中，通过引导学生观察所选模型，联系已学知识选择“等量变换或对数变换”，从而找到转化的途径．在运算过程中，如求“相关指数”引导人教版高中数学选修2-3教学设计学生使用转化后的数据，利用计算器求其相关系数即为相关指数，使学生体会使用计算器处理数据的方法和技能．11。

3.1回归分析的基本思想及其初步应用导学案周；使用时间17 年 月 日 ；使用班级 ；姓名（配合配套课件、限时练使用效果更佳）【学习目标】1.了解随机误差、残差、残差图的概念.2.会通过分析残差判断线性回归模型的拟合效果.3.掌握建立线性回归模型的步骤．【检查预习】预习相应课本，完成导学案“自主学习”部分，准备上课回答. 【自主学习】知识点一 线性回归模型思考 某电脑公司有5名产品推销员，其工作年限与年推销金额数据如下表：1．函数关系是一种__________关系，而相关关系是一种____________关系． 2．回归分析是对具有________关系的两个变量进行统计分析的一种常用方法．3．对于一组具有线性相关关系的数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )，回归直线y ^＝b ^x ＋a ^的斜率和截距的最小二乘估计公式分别为b ^＝____________＝∑i ＝1nx i y i －n x y∑i ＝1nx 2i －n x2，a ^＝________，其中________称为样本点的中心．4．线性回归模型y ＝bx ＋a ＋e ，其中a 和b 是模型的未知参数，e 称为__________，自变量x 称为____________，因变量y 称为____________． 知识点二 线性回归分析具有相关关系的两个变量的回归直线方程y ^＝b ^x ＋a ^. 思考1 预报变量y ^与真实值y 一样吗？思考2 预报值y ^与真实值y 之间误差大了好还是小了好？1．残差平方和法(1)e ^i ＝y i －y ^i ＝y i －b ^x i －a ^(i ＝1,2，…，n )称为相应于点(x i ，y i )的残差． (2)残差平方和 i ＝1n(y i －y ^i )2越小，模型拟合效果越好．2．残差图法残差点______________落在水平的带状区域内，说明选用的模型比较合适，其中这样的带状区域宽度________，说明模型的精确度越高． 3．利用相关指数R 2刻画回归效果其计算公式为：R 2＝1－________________，其几何意义：________________，表示回归效果越好． 知识点三 建立回归模型的基本步骤(1)确定研究对象，明确哪个变量是解释变量，哪个变量是预报变量．(2)画出解释变量和预报变量的散点图，观察它们之间的关系(如是否存在线性相关关系等)． (3)由经验确定回归方程的类型(如观察到数据呈线性相关关系，则选用线性回归方程y ^＝b ^x ＋a ^)．(4)按一定规则估计回归方程中的参数(如最小二乘法)．(5)得出结果后分析残差图是否有异常，若存在异常，则检查数据是否有误或模型是否合适等.【合作探究】类型一 求线性回归方程例1 某研究机构对高三学生的记忆力x 和判断力y 进行统计分析，得下表数据(1)(2)请根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归方程y ^＝b ^x ＋a ^； (3)试根据求出的线性回归方程，预测记忆力为9的同学的判断力．(相关公式：b ^＝∑i ＝1nx i y i －n x ·y∑i ＝1nx 2i －n x2，a ^＝y －b ^x )类型二 线性回归分析例2 假定小麦基本苗数x 与成熟期有效穗y 之间存在相关关系，今测得5组数据如下：(1)以x 为解释变量，(2)求y 与x 之间的回归方程，对于基本苗数56.7预报有效穗； (3)计算各组残差，并计算残差平方和；(4)求相关指数R 2，并说明残差变量对有效穗的影响占百分之几？类型三 非线性回归分析 例3 下表为收集到的一组数据：(1)作出x 与y (2)建立x 与y 的关系，预报回归模型并计算残差； (3)利用所得模型，预报x ＝40时y 的值．【学生展示】探究点一、二【教师点评】探究点三及【学生展示】出现的问题【当堂检测】1．关于回归分析，下列说法错误的是()A．在回归分析中，变量间的关系若是非确定性关系，那么因变量不能由自变量唯一确定B．线性相关系数可以是正的也可以是负的C．在回归分析中，如果r2＝1或r＝±1，说明x与y之间完全线性相关D．样本相关系数r∈(－1,1)2．如图四个散点图中，适合用线性回归模型拟合其中两个变量的是()A．①②B．①③C．②③D．③④3．下表是x和y之间的一组数据，则y关于x的回归直线必过()x 123 4y 1357A.点(2,3)C．点(2.5,4) D．点(2.5,5)4．已知x、y之间的一组数据如下表：x 012 3y 1357(1)分别计算：x、y、x1y1＋x2y2＋x3y3＋x4y4、x21＋x22＋x33＋x24；(2)已知变量x与y线性相关，求出回归方程．【小结作业】作业：本节限时练。

回归分析【教学目标】：（1）知识与技能：了解求线形回归方程的两个计算公式的推导过程，、回归平方和；了解随机误差产生的原因；了解判断刻画模型拟合效果的方法——相关指数和残差分析；了解非线性模型通过变换转化为线性回归模型。

（2）过程与方法：本节内容先从大学中女大学生的甚高和体重之间的关系入手，求出相应的回归直线方程，从中也找出存在的不足，从而有进行回归分析的必要性，进而学习相关指数，用相关指数来刻画回归的效果。

（3）情感态度与价值观：从实际问题中发现自己已有知识的不足之处，激发学生的好奇心和求知欲，培养学生不满足于已有知识，勇于求知的良好个性品质，引导学生积极进取。

【教学重点】：1.了解判断刻画模型拟合效果的方法——相关指数和残差分析；2.通过探究使学生体会有些非线性模型通过变换可以转化为线性回归模型。

【教学难点】：1.了解随机误差产生的原因，用残差平方和衡量回归方程的预报精度；2.了解判断刻画模型拟合效果的方法——相关指数和残差分析。

【教学过程设计】：教学环节教学活动设计意图一、创设情境1．由例1知，体重的值受身高或随机误差的影响。

2．问题一：身高172cm的女大学生的体重一定是60.316kg吗？如果不是，其原因是什么？引入回归分析的效果评价的三个统计量二、探究新知解答问题一：结合实例由结果分析残差图是否异常，养成从实际问题40455055606570150155160165170175180显然，身高172cm 的女大学生的体重不一定是60.316kg ，但 一般可以认为她的体重接近于60.316kg.上图3.1-2中的样本点和回归直线的相互位置说明了这一点.由于所有的样本点不共线，而只是散布在某一条直线的附近，所以身高和体重的关系可用下面的线性回归模型来表示： y=bx+a+e (3) 这里a 和b 为模型的未知参数，e 是y 与a bx y +=~之间的误差。

通常e 为随机变量，称为随机误差，它的均值E(e)=0,方差D (e)=02>σ.这样线性回归模型的完整表达式为：⎩⎨⎧==++=2)(,0)(σe D e E ea bx y (4) 在线性回归模型（4）中，随机误差e 的方差2σ越小，通过回归直线a bx y +=~（5）预报真实值y 的精度越高。

3.1 回归分析基本思想及其初步应用第二课时一、教学目标 1.核心素养:通过学习回归分析的基本思想及其初步应用，初步形成基本的数据分析能力. 2.学习目标（1）1.1.2.1 理解相关系数概念（2）1.1.2.2 判断刻画模型拟合效果的方法—相关指数和残差分析 （3）1.1.2.3 能用回归分析的方法对简单的案例进行分析. 3.学习重点判断刻画模型拟合效果的方法—相关系数、相关指数和残差分析 4.学习难点判断刻画模型拟合效果的方法—相关系数、相关指数和残差分析 二、教学设计 （一）课前设计 1.预习任务 任务1阅读教材P 4－P 6，思考在回归分析中，分析残差能够帮助我们解决那些问题？任务2刻画模型拟合效果的方法有哪些？2．预习自测1.下列说法正确的是 （ ）A.在统计学中,回归分析是检验两个分类变量是否有关系的一种统计方法B.线性回归方程对应的直线a x b yˆˆˆ+=至少经过其样本数据点1122(,),(,),,(,)n n x y x y x y L 中的一个点C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高D.在回归分析中,相关指数2R 为98.0的模型比相关指数2R 为80.0的模型拟合的效果差 【知识点：回归分析】解:C A.回归分析反映两个变量相关关系的数学方法，由建立回归方程来预报变量的情况.错误；B.线性回归方程对应的直线a x b yˆˆˆ+=，过其样本数据平均数点，错误；D.相关指数2R 越大，则相关性越强，模型的拟合效果越好. 错误；C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高. 正确.2.两个变量y 与x 的回归模型中，分别选择了4个不同模型，它们的相关指数2R 如下，其中拟合效果最好的模型是（ ） A.模型1的相关指数2R 为0.99 B.模型2的相关指数2R 为0.88 C.模型3的相关指数2R 为0.50 D.模型4的相关指数2R 为0.20 【知识点：回归分析】解:A 由相关指数的意义知，2R 越大说明相关性越强，故选A. （二）课堂设计 1.知识回顾⑴对于一组具有线性相关关系的数据1122(,),(,),,(,)n n x y x y x y L ，1211,n n i i x x x x x n n =+++==∑L 121y y y 1y y ,nn i i n n=+++==∑L 则称点),y x （为样本点的中心. （2）线性回归方程：∧∧∧+=a x b y ，其中.1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑，a ∧=x b ∧-y（3）线性回归模型：y =bx +a +e 其中a 和b 为模型的未知参数，e 称为随机误差. 2.问题探究问题探究一 什么是相关系数？相关系数可以用来解释什么？●活动一 理论研究，概念学习—相关系数我们知道，两个变量x 和y 正（负）相关时，它们就有相同（反）的变化趋势，因此可以用回归直线来描述这种关系.与此相关的一个问题：如何描述x 和y 之间种线性关系的强弱？在统计中用相关系数r 来衡量两个变量之间线性关系的强弱.若相应于变量x 的取值i x ，变量y 的观测值为i y （n i ≤≤1），则两个变量的相关系数r 的计算公式为∑∑∑===----=ni ni iini iiy yx x y yx x r 11221)()())((对于相关系数r ，当为正时，表明变量x 和y 正相关，当r 为负时，表明变量x 和y 负相关. 统计学认为，对于变量x,y ，如果[]75.0,1--∈r ，那么负相关很强；如果[]1,75.0∈r ，那么正相关很强；如果(]30.0,75.0--∈r 或[)75.0,3.0∈r ，那么相关性一般；若[]25.0,25.0-∈r ，那么相关性较弱.●活动二 学以致用，相关系数的应用例1 对下列各图中两个变量间的线性相关程度作出分析【知识点：相关系数】详解：图1，r =0.97相关性很强，而且是正相关；图2，r =-0.85相关性很强，而且是负相关 图3，r =0.24，不能用线性回归模型描述两个变量的关系；图4，r =-0.05乎没有什么关系，不能用线性回归模型描述两个变量的关系.点拨：当相关系数r 越接近1时，两个变量的线性相关程度越高，当相关系数r 越接近0时，两个变量的线性相关程度越低.问题探究二 什么是残差、及残差平方和、如何用残差判断拟合效果？ ●活动一 残差的定义在线性回归模型中，e 是用bx +a 报真实值y 的随机误差，它是一个不可观测的量，那么应该怎样研究随机误差呢？在实际应用中，我们用回归方程∧∧∧+=a x b y 中的∧y 估计回归模型y =bx +a +e 中的bx +a .由于随机误差e =y -(bx +a )，所以∧∧-=y y e 是e 的估计值.对于样本点1122(,),(,),,(,)n n x y x y x y L 而言，它们的随机误差为,1,2,,i i i e y bx a i n =--=L 其估计值为∧∧∧∧--=-=a x b y y y e i i i i i 1,2,,i n =L 称i e ∧是相对于点),i i y x （的残差. ●活动二 学以致用，残差的应用如何发现数据中的错误，如何衡量模型的拟合效果？通过残差可以发现原始数据中的可疑数据，判断所建立模型的拟合效果.下表是女大学生身高和体重的原始数据以及相应的残差数据.我们可以利用图形来分析残差.作图时纵坐标为残差，横坐标可以选为样本的编号或者解释变量的数值，这样作出的图形称为残差图.下表是以女大学生编号为横坐标的残差图从残差图中可以看到第1个样本点和第6个样本点的残差较大，需要确认是否出现人为的错误.残差所能说明的情况：① 样本点的残差比较大，确认采集数据时是否出现人为的错误或其他原因；②残差点比较均匀地落在水平的带状区域中，说明选用的模型比较合适，带状区域的宽度越窄，模型拟合精度越高，回归方程的预报精度越高.●活动三 多角度刻画拟合效果从残差图中我们可以大致判断模型的拟合效果，能否定性分析模型的拟合效果呢？ 我们可以用2R 是刻画回归效果的量，除了表示回归模型的拟合效果，也表示解释变量和预报变量的线性相关关系（在线性回归模型中）.其计算公式是22121ˆ()1()ni i nii y yR y y ==-=--∑∑对于已获取的样本数据，2R 表达式中的()∑=-ni i y y 12为确定的数.因此2R 越大，说明残差平方和()21ˆni i y y=-∑越小，模型的拟合效果越好；2R 越小，说明残差平方和()21ˆni i y y =-∑越大，模型的拟合效果越差.在线性回归模型中，2R 越接近于1，回归的效果越好（因为2R 越接近于1，表示解释变量和预报变量的线性相关性越强）.在线性回归模型中，2R 同时也表示解释变量对预报变量变化的贡献率.()()64.0ˆ112122≈---=∑∑==ni ini i i y yy y R ，即解释变量对预报变量变化约贡献了64%，而随机误差贡献了剩余的36%. 问题探究三●活动一 学以致用例2.某运动员训练次数与运动成绩之间的数据关系如下：根据数据分别计算相关系数、残差、相关指数2R ，判断能否用线性回归模型，若能求出回归方程并试预测该运动员训练47次以及55次的成绩，若不能说明理由. 【知识点：线性回归，线性相关关系】详解：（1）作出该运动员训练次数x 与成绩y 之间的散点图，如图1所示，由散点图可知，它们之间具有线性相关关系.（2）列表计算：由上表可求得875.40,25.39==y x ，12656812=∑=i ix ，13731812=∑=i iy ，1318081=∑=ii i yx ，所以88118822211()()8 1.0415.()iii ii i iii i x x y y x y x yb x x xx====---==≈--∑∑∑∑00302.0-≈-=x b y a ，所以回归直线方程为.00302.00415.1^-=x y（3）计算相关系数将上述数据代入0.992704r r ==，查表可知707.005.0=r ，而05.0r r >，故y 与x 之间存在显著的相关关系. （4）残差分析：作残差图如图2，由图可知，残差点比较均匀地分布在水平带状区域中，说明选用的模型比较合适.计算残差的方差得884113.02=σ，说明预报的精度较高. （5）计算相关指数2R计算相关指数2R ＝0.9855.说明该运动员的成绩的差异有98.55％是由训练次数引起的. （6）做出预报由上述分析可知，我们可用回归方程.00302.00415.1^-=x y 作为该运动员成绩的预报值.将x ＝47和x ＝55分别代入该方程可得y ＝49和y ＝57， 故预测运动员训练47次和55次的成绩分别为49和57.点拨：1.解答本类题目应先通过散点图来分析两变量间的关系是否线性相关，然后再利用求回归方程的公式求解回归方程，并利用残差图或相关指数R 2来分析函数模型的拟合效果，在此基础上，借助回归方程对实际问题进行分析. 2.在使用回归方程进行预报时要注意：(1)回归方程只适用于我们所研究的样本的总体； (2)我们所建立的回归方程一般都有时间性； (3)样本取值的范围会影响回归方程的适用范围；(4)不能期望回归方程得到的预报值就是预报变量的精确值. 3.课堂总结【知识梳理】（1）在统计中用相关系数r 来衡量两个变量之间线性关系的强弱.若相应于变量x 的取值i x ，变量y 的观测值为i y （n i ≤≤1），则两个变量的相关系数r 的计算公式为∑∑∑===----=ni ni iini iiy yx x y yx x r 11221)()())((（2）数据点和它在回归直线上相应位置的差异是随机误差的效应，称(1,2,3,n)i i e y y i ∧∧=-=L ,为残差.由,y ∧∧∧+=a x b i i 得(1,2,3,,)i i i e y b x a i n ∧∧∧=--=L .【重难点突破】（1）残差图分析：若残差点比较均匀地落在水平的带状区域中，说明选用的模型比较合适，这样的带状区域的宽度越窄，说明模型拟合精度越高，回归方程的预报精度就越高.若残差点分布在其他形状的区域，则说明所选用的回归模型不是最好的，有改进的空间.（2）2R 越大，说明残差平方和21)y (∑=-ni i y 越小，模型的拟合效果越好；2R 越小，说明残差平方和21)y (∑=-ni i y 越大，模型的拟合效果越差．在线性回归模型中，2R 越接近于1，回归的效果越好（因为2R 越接近于1，表示解释变量和预报变量的线性相关性越强）.在线性回归模型中， 2R 同时也表示解释变量对预报变量变化的贡献率. 4.随堂检测1.下列各组变量之间具有线性相关关系的是（ ） A.出租车费与行驶的里程 B.学习成绩与学生身高 C.身高与体重 D.铁的体积与质量【知识点：线性回归，线性相关关系】解: C2.已知x 与y 之间的几组数据如下表：假设根据上表数据所得线性回归直线方程y ^＝b ^x ＋a ^，若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y ＝b ′x ＋a ′，则以下结论正确的是（ ） A.b ^>b ′，a ^>a ′B.b ^ >b ′，a ^ <a ′C.b ^<b ′，a ^>a ′ D.b ^ <b ′，a ^<a ′【知识点：线性回归，线性相关关系】解:C b ′＝2，a ′＝－2，b ^ ＝57，a ^ ＝y －b ^ x ＝136－57×72＝－13， ∴b ^ <b ′，a ^>a ′.选C.3.四名同学根据各自的样本数据研究变量y x ,之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y 与x 负相关且1.63.2-=∧x y ； ②y 与x 负相关且1.537.3--=∧x y ； ③y 与x 正相关且27.3-=∧x y ； ④y 与x 正相关且17.656.4+-=∧x y . 其中一定不正确的结论的序号是（ ） A.①② B.②③ C.③④ D.①④【知识点：线性回归，线性相关关系】解：D ①中y 与x 负相关而斜率为正，不正确；④中y 与x 正相关而斜率为负，不正确. 4.如果散点图中的所有的点都在一条斜率不为0的直线上，则残差为_____，相关指数2R ＝_____. 【知识点：线性回归，线性相关关系】解：0， 1 由题意知，ˆi i y y = ∴相应的残差ˆˆ0i i i ey y =-=. 相关指数22121ˆ()110 1.()niii nii y yR y y ==-=-=-=-∑∑（三）课后作业 基础型 自主突破1.对四组数据进行统计，获得以下散点图，关于其相关系数比较，正确的是（ ）相关系数为1r 相关系数为2r相关系数为3r 相关系数为4r A.24310r r r r <<<< B.31240r r r r <<<< C.13240r r r r <<<< D.31420r r r r <<<< 【知识点：相关系数】解：A2. 甲、乙、丙、丁四位同学在建立变量y x ,的回归模型时，分别选择了4中不同的模型，计算可得它们的相关指数2R 分别如下表，其中拟合效果最好的为（ ）A.甲B.乙C.丙D.丁 答案：A解析：【知识点：相关指数】3.已知变量x 与y 正相关，且由观测数据算得样本平均数x －＝3，y －＝3.5，则由该观测数据算得的线性回归方程可能是（ ） A.y ^＝0.4x ＋2.3 B.y ^＝2x －2.4 C.y ^＝－2x ＋9.5 D.y ^＝－0.3x ＋4.4【知识点：回归方程，相关关系】解：A 因为变量x 和y 正相关，则回归直线的斜率为正，故可以排除选项C 与D.因为样本点的中心在回归直线上，把点(3，3.5)的坐标分别代入选项A 和B 中的直线方程进行检验，可以排除B ，只有A 可能.4.已知一组观测值1122,),(,),,(,)n n x y x y x y L （之间满足(1,2,,)y bx a e i n =++=L ，若e 恒为0，则2R 为 .【知识点：残差，相关指数】 答案：1.5.下表中给出了5组数据),(i i y x ，从中选出4组使其线性相关性最大，且保留第1组（-5，-3），那么应该去掉第_______组【知识点：残差分析】解： 3能力型 师生共研6.设两个变量x 和y 之间具有线性相关关系，它们的相关系数是r ，y 关于x 的回归方程的回归系数是∧b ，回归截距是∧a ，那么必有（ ） A .∧b 与r 的符号相同 B .∧a 与r 的符号相同 C .∧b 与r 的相反D .∧a 与r 的符号相反 【知识点：相关关系】解：.A ∧b 决定正相关还是负相关，与r 的符号相同.7.回归分析中，相关指数2R 的值越大，说明残差平方和（ ） A.越小 B.越大C.可能大也可能小D.以上都不对【知识点：相关指数】解： A 由2R 和残差平方和公式易得.8. 若对于变量y 与x 的10组统计数据的回归模型中，相关指数95.02=R ，又知残差平方和为53.120，那么∑=-1012)(i iy y的值为（ ）A.241.06B.2410.6C.253.08D.2530.8【知识点：相关指数】解： B 由2R 和残差平方和公式易得. 9.已知x ，y 之间的一组数据如下表：对于表中数据，现给出如下拟合直线：①5457+=x y ；②12+=x y ；③52-58x y =；④x y 2=.根据最小二乘法的思想，其中拟合程度最好的直线是________.(填正确序号) 【知识点：样本点中心，回归方程】解：① 直线必过样本点中心（3,5），依次检验即可. 探究型 多维突破（一般为2道题，具体课时可相应灵活调整）10.假定小麦基本苗数x 与成熟期有效穗y 之间存在相关关系，现测得5组数据如下表：（1）以x 为解释变量，y 为预报变量，作出散点图；（2）球y 与x 间的回归方程，对于基本苗数56.7，预报其成熟期的有效穗；（3）求相关指数2R ，并说明残差变量对成熟期有效穗的影响占百分之几. 【知识点：散点图，回归方程，相关指数】 解：（1）略（2）由散点图可知，样本点呈条状分布，有比较好的线性相关关系，因此可以用线性回归方程刻画它们之间的关系.可求得线性回归方程为.291.0664.34x y +=∧当x =56.7时，.164.517.56291.0644.34≈⨯+=∧y 即估计其成熟期有效穗为51.164. （3）残差平方和为：,427.8512≈∑=i i e总偏差平方和：,18.50)512≈-∑=i i y y （故，832.018.50427.8-12≈=R 解释变量小麦基本苗数对成熟期有效穗的影响约占83.2%，残差变量的影响约占1-83.2%=16.8%.11.一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次试验，测得数据如下：（1）计算残差及残差和; （2）进行残差分析.【知识点：残差，残差分析，残差图】解：（1） 列出残差表（由已知可知7.91960.54668.0=+=∧y x y ，）如下所以残差平方和=2220.4-0.30.2 1.4+++=L （）（）（），残差值如表中第四行的值.（2）残差分析：画出残差图，散点图（略），由散点图可以说明x 与y 有很强的相关性.可以观察到，第4个样本点和第5个样本点的残差比较大，需要纠正数据，重新利用线性回归模型拟合数据；残差图中的残差点比较均匀地落在水平的带状区域中，说明选用的线性回归模型较为合适，带状区域的宽度仅为1.3，比较狭窄，说明模型拟合精度较高. （四）自助餐1.从某大学随机抽取8名女大学生，其身高x （cm ）和体重y （kg ）的回归方程为712.85-849.0x y =∧，则身高172cm 的女大学生，由回归方程可以得知其体重（ ） A.等于60.316kg B.约为60.316kg C.大于60.316kg D.小于60.316kg 【知识点：回归分析】 解：B2.在回归分析中，残差图的纵坐标为（ ） A.残差 B.样本编号 C.等高条形图 D.独立性检验 【知识点：残差图】 解： A3.设1122(,)(,),,(,)n n x y x y x y L 是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论正确的是（ ）A.直线l 过点(,)x yB.x 与y 的相关系数为直线l 的斜率C.x 与y 的相关系数在0到1之间D.当n 为偶数时，分布在l 两侧的样本点的个数一定相同 【知识点：回归分析，相关系数】 解：A4.对两个变量x 和y 进行回归分析,得到一组样本数据: 1122(,)(,),,(,)n n x y x y x y L ，则下列说法中不正确的是（ ）A.由样本数据得到的回归方程ˆˆˆybx a =+必过样本点的中心(,)x y B.残差平方和越小的模型,拟合的效果越好C.用相关指数R 2来刻画回归效果,R 2的值越小,说明模型的拟合效果越好D.若变量y 和x 之间的相关系数r =-0.936 2,则变量y 和x 之间具有线性相关关系 【知识点：回归分析，相关系数】解： C 解析:R 2的值越大,说明残差平方和越小,也就是说模型的拟合效果越好. 5.如图所示的是四个残差图，其中回归模型的拟合效果最好的是（ ）【知识点：残差图】解：B 残差图中，只有A 、B 是水平带状区域分布，且B 中残差点散点分布集中在更狭窄的范围内所以B 项中回归模型的拟合效果最好.6.变量x 与y 具有线性相关关系，当x 取值16，14，12，8时，通过观测得到y 的值为别为11，9，8.5.若在实际问题中，y 的最大取值是10，则x 的最大取值不能超过（ ） A.16 B.17 C.15 D.12【知识点：回归方程】 解：C7.一家工厂对职工进行技能培训，收集数据如下：两变量的回归直线方程为__________,该函数模型的残差平方和为__________,相关指数为__________.【知识点：回归方程，残差，相关指数】 解：. 5.9817.0+=∧x y 34.126 957.0.8.若回归直线方程中的参数0=∧b ，则相关系数为 . 【知识点：相关系数】 解：0.9.关于x 与y 有如下数据为了对x ，y 两个变量进行统计分析，现有以下两种线性模型，甲：5.175.6+=∧x y ，乙：177+=∧x y ，则模型__________拟合效果更好.（填“甲”或“乙”） 【知识点：回归分析，样本点中心】 解：甲.10.关于x 与y 有以下数据:已知x 与y 线性相关,由最小二乘法得ˆb =6.5, (1)求y 关于x 的线性回归方程.(2)现有第二个线性模型:ˆy=7x +17,且相关指数R 2=0.82.若与(1)的线性模型比较,哪一个线性模型拟合效果比较好?请说明理由. 【知识点：回归分析，相关指数】解:(1)依题意设y 关于x 的线性回归方程为ˆˆ6.5yx a =+, 1(24568)=55x =⨯++++，1(3040605070)=505y =⨯++++∵ˆˆ6.5yx a =+经过样本点的中心(,)x y , ∴50=6.5×5+ˆa,∴ˆa =17.5, ∴y 与x 的线性回归方程为ˆy=6.5x +17.5. (2)由(1)的线性模型得ˆi i y y -与i y y -的关系如下表:所以52222221ˆ()(0.5)( 3.5)10( 6.5)0.5155i i i y y=-=-+-++-+=∑， 52222221()(20)(10)100201000ii y y =-=-+-+++=∑，所以52211521ˆ()155110.8451000()iii ii y yR y y ==-=-=-=-∑∑. 由于21R =0.845,R 2=0.82知21R >R 2, 所以(1)的线性模型拟合效果比较好.11.假设关于某设备的使用年限x (年)和所支出的维修费用y (万元)有关的统计资料如表所示.(1)求线性回归方程ˆˆˆybx a =+； (2)若相关指数R 2＝0.9587，说明其含义； (3)估计使用年限为9年时，维修费用是多少？ 【知识点：回归分析，相关指数】 解：(1)由已知数据制成表：由此可得x ＝4，y ＝5，121()()1.23()niii nii x x y y b x x ∧==--==-∑∑，ˆˆ0.08ay bx =-= ∴回归直线方程为ˆy＝1.23x ＋0.08. (2)R 2＝0.958 7，说明该设备的维修费用有95.87%由使用年限引起的.所以回归模型的拟合效果好.(3)回归直线方程为ˆy ＝1.23x ＋0.08，当x ＝9（年）时，ˆy ＝1.23×9＋0.08＝11.15(万元)，即估计使用9年时维修费用是11.15万元.。

3.2 回归分析学案（人教B版高中数学选修2-3）3.2回归分析回归分析学习目标1.会建立线性回归模型分析两个变量间的相关关系.2.能通过相关系数判断两个变量间的线性相关程度知识点一回归分析及回归直线方程思考1什么叫回归分析答案回归分析是对具有相关关系的两个变量进行统计分析的一种方法思考2回归分析中，利用回归直线方程求出的函数值一定是真实值吗答案不一定是真实值，利用回归直线方程求的值，在很多时候是个预测值梳理1回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法若两个变量之间具有线性相关关系，则称相应的回归分析为线性回归分析2回归直线方程为ybxa，且bi1nxixyiyi1nxix2，aybx，其中x1ni1nxi，y1ni1nyi，x，y称为样本点的中心，回归直线一定过样本点的中心知识点二相关系数1对于变量x与Y随机抽到的n对数据x1，y1，x2，y2，，xn，yn，检验统计量是样本相关系数rni1xixyiyni1xix2ni1yiy2ni1xiyinxyni1x2inx2ni1y2iny2.2相关系数r的取值范围是1,1，|r|越接近1，变量之间的线性相关程度越强；|r|越接近0，变量之间的线性相关程度越弱当|r|r0.05时，表明有95的把握认为两个变量之间具有线性相关关系1求回归直线方程前可以不进行相关性检验2利用回归直线方程求出的值是准确值类型一回归直线方程例1若从某大学中随机选取8名女大学生，其身高和体重数据如下表所示编号_________12345678身高/cm165165157170175165155170体重/kg4857505464614359求根据女大学生的身高预测体重的回归直线方程，并预测一名身高为172cm的女大学生的体重考点线性回归分析题点回归直线的应用解1画散点图选取身高为自变量x，体重为因变量y，画出散点图，展示两个变量之间的关系，并判断二者是否具有线性关系由散点图可以发现，样本点呈条状分布，身高和体重有比较好的线性相关关系，因此可以用回归直线方程ybxa 来近似刻画它们之间的关系2建立回归方程由计算器可得b0.848，a85.632.于是得到回归直线方程为y0.848x85.632.3预测和决策当x172时，y0.84817285.63260.224kg即一名身高为172cm的女大学生的体重预测值为60.224kg.反思与感悟在使用回归直线方程进行预测时要注意1回归直线方程只适用于我们所研究的样本的总体2我们所建立的回归直线方程一般都有时间性3样本取值的范围会影响回归直线方程的适用范围4不能期望回归直线方程得到的预测值就是因变量的精确值跟踪训练1假设关于某设备的使用年限x年和所支出的维修费用y万元有如下的统计数据x23456y2.23.85.56.57.0由此资料可知y对x呈线性相关关系1求回归直线方程；2求使用年限为10年时，该设备的维修费用为多少考点回归直线方程题点求回归直线方程解1由题干表中的数据可得x4，y5，i15x2i90，i15xiyi112.3，bi15xiyi5xyi15x2i5x2112.3545905421.23，aybx51.2340.08.回归直线方程为y1.23x0.08.2当x10时，y1.23100.0812.38.即使用年限为10年时，该设备的维修费用约为12.38万元类型二相关性检验例2维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y来衡量，这个指标越高，耐热水性能也越好，而甲醛浓度是影响缩醛化度的重要因素，在生产中常用甲醛浓度xg/L 去控制这一指标，为此必须找出它们之间的关系，现安排一批实验，获得如下数据甲醛浓度g/L18202224262830缩醛化度克分子26.8628.3528.7528.8729.7530.0030.361画散点图；2求回归直线方程；3求相关系数r，并进行相关性检验考点线性相关系数题点线性相关系数的概念及计算解1散点图如图2可以看出，两变量之间有近似的线性相关关系，下面用列表的方法计算a，b.ixiyix2ixiyi11826.86324483.4822028.3540056732228.75484632.542428.87576692.8852629.75676773.562830.0078484073030.36900910.80168202.9441444900.16x168724，y202.947，b7i1xiyi7xy7i1x2i7x24900.16724202.947414472420.2643，aybx202.9470.26432422.648，回归直线方程为y22.6480.2643x.37i1y2i5892，r7i1xiyi7xy7i1x2i7x27i1y2i7y24900.16724202.94741447242589 27202.94720.96.r0.96r0.050.754.有95的把握认为“甲醛浓度与缩醛化度有线性相关关系”，求得的回归直线方程有意义反思与感悟根据已知数据求得回归直线方程后，可以利用相关系数和临界值r0.05比较，进行相关性检验跟踪训练2为了研究3月下旬的平均气温x与4月20日前棉花害虫化蛹高峰日y的关系，某地区观察了xx年至xx年的情况，得到了下面的数据年份xxxxxxxxxxxxx24.429.632.930.328.9y日196110181对变量x，y进行相关性检验；2据气象预测，该地区在xx年3月下旬平均气温为27，试估计xx年4月化蛹高峰日为哪天考点线性相关系数题点线性相关系数的概念及计算解由已知条件可得下表i123456xi24.429.632.928.730.328.9yi19611018x29.13，y7.5，i16x2i5130.92，i16y2i563，i16xiyi1222.61ri16xiyi6xyi16x2i6x2i16y2i6y20.9341.查表知r0.050.811.由|r|r0.05可知，变量y和x存在线性相关关系2b1222.6629.137.55129.1322.23，aybx72.46.所以回归直线方程为y2.23x72.46.当x27时，y2.232772.4612.据此，可估计该地区xx年4月12日为化蛹高峰日.1某商品销售量y件与销售价格x元/件呈负相关，则其回归直线方程可能是A.y10x200B.y10x200C.y10x200D.y10x200考点题点答案A解析由于销售量y与销售价格x成负相关，故排除B，D.又当x10时，A中y100，而C中y300，C不符合题意，故选A.2下表是x和y之间的一组数据，则y关于x的回归直线必过x1234y1357A.点2,3B点1.5,4C点2.5,4D点2.5,5考点回归直线方程题点样本点中心的应用答案C解析回归直线必过样本点中心x，y，即2.5,43对变量y和x进行相关性检验，已知n为数据的对数，r是相关系数，且已知n3，r0.9950；n7，r0.9533；n15，r0.3012；n17，r0.4991.则变量y和x具有线性相关关系的是A和B和C和D和考点线性相关系数题点线性相关系数的应用答案C解析当n3时，r0.050.997，所以|r|r0.05，表明有95的把握认为x与y之间具有线性相关关系；当n15时，r0.050.514，所以|r|r0.05，表明有95的把握认为x与y之间具有线性相关关系，所以和满足题意，故选C.4某产品在某零售摊位的零售价x单位元与每天的销售量y 单位个的统计资料如下表所示x16171819y50344131由上表可得回归直线方程ybxa中的b5，据此模型预测当零售价为14.5元时，每天的销售量为A51个B50个C54个D48个考点线性回归分析题点回归直线方程的应用答案C解析由题意知x17.5，y39，代入回归直线方程得a126.5,126.514.5554，故选C.5已知x，y之间的一组数据如下表x0123y13571分别计算x，y，x1y1x2y2x3y3x4y4，x21x22x23x24；2已知变量x与y线性相关，求出回归直线方程考点回归直线方程题点求回归直线方程解1x012341.5，y135744，x1y1x2y2x3y3x4y40113253734，x21x22x23x240212223214.2b3441.541441.522，aybx421.51，故回归直线方程为y2x1.1对具有线性相关关系的两个变量进行统计分析，可从散点图观察大致呈条状分布，可以求回归直线方程并进行预报2通过求相关系数并和临界值r0.05比较可以判断两个变量是否有线性相关关系，求得的回归直线方程是否有意义.。

第3章 统计案例3.1 回归分析基本思想及其初步应用第一课时一、教学目标 1.核心素养:通过学习回归分析的基本思想及其初步应用，初步形成基本的数据分析能力. 2.学习目标（1）1.1.1.1 温习散点图,复习相关关系与函数关系.（2）1.1.1.2 理解回归分析的基本思想，会求线性回归方程.（3）1.1.1.3 理解回归模型与函数模型的差别，了解随机误差产生的原因. 3.学习重点线性回归分析的一般步骤，,回归分析的应用. 4.学习难点理解随机误差产生的原因以及函数模型与回归模型的差别. 二、教学设计 （一）课前设计 1.预习任务 任务1阅读教材P 2－P 4，思考求解线性回归方程一般步骤是什么？回归模型和函数模型有何区别？随机误差产生的原因？ 任务2什么是解样本中心点，什么是回归分析？2.预习自测 1.两个变量有线性相关关系且正相关，则回归直线方程中，a bx y +=的系数b （ ）A.0>bB.0<bC.0=bD.1=b解：A2.在画两个变量的散点图时，下面哪个叙述是正确的（ ） A.预报变量在x 轴上，解释变量在y 轴上 B.解释变量在x 轴上，预报变量在y 轴上 C.可以选择两个变量中任意一个变量在x 轴上D.可以选择两个变量中任意一个变量在y 轴上 解：B3.回归直线y bx a =+必过（ ）A. (0,0)B. (,0)xC. (0,)yD. (,)x y 解：D （二）课堂设计 1.知识回顾（1）线性回归方程：∧∧∧+=a x b y ，其中.1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑， ˆy ab x ∧=- （2）线性相关：如果所有点看上去都在一条直线附近波动，则两个变量间是线性相关，可用一条直线来近似表示（3）非线性相关：若所有点看上去都在某条曲线附近波动，则两个变量间是非线性相关，可用一条曲线来拟合.（4）回归分析：是对具有相关关系的两个变量进行的统计分析的一种常用方法. 2.问题探究问题探究一 相关关系与函数关系是什么，如何画散点图？ ●活动一 回顾旧知，回忆相关关系与函数关系在《必修3》中，我们已经学习过函数关系与相关关系，那么什么是函数关系，什么是相关关系?想一想：在以往数学学习和日常生活中，我们接触了哪些函数关系与相关关系？ 举例：请大家试着列举生活与学习中的相关例子.例如圆的周长2C r π=，周长C 与半径r 之间就是一种确定性的关系，对于自变量半径的每一个确定的值，都有唯一确定的周长的值与之相对应.又如人的体重y 与身高x ，一般来说，身高越高，体重越重，但不能用一个函数来严格表示它们之间的关系.即变量之间有一定的联系，但取值也具有一定的随机性.即： 1. 函数关系与相关关系 （1） 函数关系是一种确定关系. （2） 相关关系是一种不确定关系.注意：判断两个变量是否具有相关关系，应该先看它们是否有关，再看这种关系是否是确定的函数关系.●活动二 旧知推进，回忆散点图的画法 2. 散点图在分析两个变量的关系时，为了对变量之间的关系有一个大概的了解，我们通常将一个变量的数据作为横坐标，另一个变量的数据作为纵坐标，将这些点描在平面直角坐标系中，形成的图形就是散点图（1）散点图直观反映了实例的成对观测值之间是否存在相关关系和存在什么样的相关关系. （2）若散点图中点的分布由左下方到右上方，则两个变量正相关；点的分析由左上方到右下方，则两个变量负相关问题探究二 线性回归分析步骤是什么？●活动一 通过实例，亲身体验在《必修3》中，我们利用回归分析的方法对两个具有线性相关关系的变量进行了研究，你能利用回归分析对下列实例进行分析吗？例1 从某大学中随机选取8名女大学生，其身高和体重数据如下表所示：求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为172cm 的女大学生的体重.【知识点：线性回归方程，回归分析；】详解：(1) 作散点图，由于问题是根据身高预报体重，因此要求身高与体重的回归直线方程，取身高为自变量x ，体重为因变量y ，作散点图：40455055606570150155160165170175180从散点图可以看出，样本点呈条状分布，身高和体重有比较好的线性相关关系，因此可以用回归直线y =bx +a 来近似刻画它们之间的关系，从而可利用我们学过的最小二乘估计思想及计算公式求得线性回归直线方程.其计算公式如下：1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑，y a b x ∧∧=-其中1211,n n i i x x x x x n n =+++==∑…121y y y 1y y ,nn i i n n=+++==∑…根据上面公式，可以得到712.85,849.0-==∧∧a b 于是得到线性回归方程712.85849.0-=∧x y对于身高172cm 女大学生，由回归方程可以预报体重为)(316.60712.85172849.0kg y =-⨯=∧，预测身高为172cm 的女大学生的体重为约60.316kg.点拨：回归分析的基本过程： （1）画出两个变量的散点图； （2）判断是否线性相关；（3）求回归直线方程（利用最小二乘法）； （4）并用回归直线方程进行预报 ●活动二 整理旧知，得出新概念 1.样本中心点对于一组具有线性相关关系的数据1122(,),(,),,(,)n n x y x y x y ，1211,nni i x x x x x n n=+++==∑121y y y 1y y ,nni i n n=+++==∑则称点),y x （为样本点的中心.●活动三 总结反思，得出新结论 由上计算过程可以得出：（1）样本点的中心坐标分别是两个变量的观测数据的算术平均数. （2）点),y x （在回归直线上，即回归直线一定过样本点的中心.问题探究三 线性回归模型与函数模型有何差异，随机误差是怎么产生的？？●活动一结合实际，反思结果想一想：身高为172cm 的女大学生的体重一定是60.316kg吗?如果不是，你能解释一下原因吗？答：不一定，但一般可以认为她的体重在60.316kg左右.由样本点和回归直线的相互位置可以说明这一点.从散点图可观察出，女大学生的体重y和身高x之间的关系并不能用一次函数y=bx+a来严格刻画（因为所有的样本点不共线，所以线性模型只能近似地刻画身高和体重的关系）. 在数据表中身高为165cm的3名女大学生的体重分别为48kg、57kg和61kg，如果能用一次函数来描述体重与身高的关系，那么身高为165cm的3名女在学生的体重应相同. 这就说明体重不仅受身高的影响还受其他因素的影响，这时我们把身高和体重的关系可用下面的线性回归模型y=bx+a+e来表示，其中a和b为模型的未知参数，e称为随机误差.●活动二层层推进，答疑解惑那么，产生随机误差项e的原因是什么呢？实际上，一个人的体重除了受身高影响外，还受其他许多因素的影响，例如饮食习惯、是否喜欢运动、度量误差等.另一方面，没有人知道身高和体重之间的真正关系是什么，现在只是利用线性回归方程来近似这种关系.而这种近似和上面提到的影响因素都会导致随机误差e的产生.即随机误差产生的原因：（1）线性回归方程中的∧b和∧a为估计值，与真实值b和a之间存在误差.（2）影响变量y的因素不止变量x一个，可能还包括许多因素（例如农作物的生长不仅要收日照时间的影响，还会受土壤的肥沃程度，施肥量等影响）（3）观测误差，由于测量工具及测量值一般也存在一定的误差，这样的误差也包含在e中所以随机误差e中包含体重不能由身高的线性函数解释的所有部分. 当残差变量恒等于0时，线性回归模型就变成一次函数模型. 因此，一次函数模型是线性回归模型的特殊形式，线性回归模型是一次函数模型的一般形式.●活动三新知学习在统计中，我们把自变量x称为解释变量，因变量y称为预报变量.线性回归模型与我们熟知的一次函数模型的不同之处就在于增加了随机误差e，预报变量y的值由解释变量x和随机误差e共同决定，即解释变量x只能解释部分预报变量y的变化3.课堂总结【知识梳理】(1)线性回归方程：∧∧∧+=a x b y ，其中.1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑，a ∧=x b ∧-y(2)回归分析的基本过程：①画出两个变量的散点图；②判断是否线性相关，③求回归直线方程（利用最小二乘法），④并用回归直线方程进行预报(3)对于一组具有线性相关关系的数据1122(,),(,),,(,)n n x y x y x y ，1211,nni i x x x x x n n=+++==∑121y y y 1y y ,nni i n n=+++==∑则称点),y x （为样本点的中心.(4)线性回归模型：y =bx +a +e ，其中a 和b 为模型的未知参数，e 称为随机误差.【重难点突破】(1)利用回归分析的方法对两个具有线性相关关系的变量进行研究的步骤： ①作出散点图 ②求回归直线方程 ③利用所求方程进行预测.（2） 随机误差产生的原因：①线性回归方程中的∧b 和∧a 为估计值，与真实值b 和a 之间存在误差.②影响变量y 的因素不止变量x 一个，可能还包括许多因素（例如农作物的生长不仅要收日照时间的影响，还会受土壤的肥沃程度，施肥量等影响）③观测误差，由于测量工具及测量值一般也存在一定的误差，这样的误差也包含在e 中. 4.随堂检测1.下面两个变量间的关系不是函数关系的是() A.正方体的棱长与体积 B.角的度数与它的正弦值C.单位产量为常数时,土地面积与粮食总产量 D.日照时间与水稻亩产量【知识点：函数关系，相关关系】解：D2. 设有一个回归方程为25.2+-=∧x y ，则变量x 增加一个单位时，y 的值得变化情况是（ ） A.平均增加2.5个单位 B.平均增加2个单位 C.平均减少2.5个单位 D.平均减少2个单位【知识点：回归方程，函数】 答案：C3. 为了研究两个变量x 与y 之间的线性相关性，甲、乙两个同学并且利用线性回归方法，求得回归直线分别为1l 和2l ，已知在两个人的试验中发现y x 和分别相等，那么下列说法正确的是（ ）A.1l 与2l 一定平行B. 1l 与2l 重合C.1l 与2l 相交于点),y x （D.无法判断1l 与2l 是否相交【知识点：回归方程，样本点中心】 答案：C4.为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程∧∧∧+=a x b y ，其中 x b y a b ^^,76.0-==∧，据此估计，该社区一户收入为15万元家庭年支出为（ ） A. 11.4万元 B. 11.8万元 C.12.0万元 D.12.2万元【知识点：回归方程，回归分析】 答案：B5.已知x 与y 有如下数据：则y 关于x 的回归直线方程∧∧∧+=a x b y 必过点 . 【知识点：回归方程，样本点的中心】 解：（1.5,5） （三）课后作业 基础型 自主突破1.对具有相关关系的两个变量统计分析的一种常用的方法是（ ） A.回归分析 B.相关系数分析 C.残差分析 D.相关指数分析 【知识点：回归分析】 解：A2.对于具有线性相关关系的变量x 和y ，由测得的数据已求得回归直线的斜率为 6.5，且恒过点（2,3），则回归直线的方程为 . 【知识点：回归方程，样本点的中心】 解：105.6-=∧x y3.一位母亲记录了儿子3—9岁的身高，数据（略），由此建立的身高与年龄的回归模型为y =7.19x +73.93，用这个模型预测这个孩子10岁时的身高，则正确的叙述是（ ） A.身高一定是145.83cm B.身高在145.83cm 以上 C.身高在145.83cm 左右 D.身高在145.83cm 以下【知识点：回归方程，回归分析】 答案：C4.为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了他某月1号到5号每天打篮球的时间x （单位：小时）与当天投篮命中率y 之间的关系：小李这5天平均投篮命中率为________;用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率为_______.【知识点：回归方程，样本点的中心】 解：0.5，0.53 能力型 师生共研1.在一次实验中，测得（x ，y ）的四组值分别是A （1，2）、B （2，3）、C （3，4）、D （4，5），则y 与x 之间的回归直线方程为（ ）A.1ˆ+=x yB.2ˆ+=x yC.12ˆ+=x yD.1ˆ-=x y【知识点：回归直线方程】 解：A2.如果某地的财政收入x 与支出y 满足线性回归方程e a bx y ++=∧（单位：亿元），其中5.0||,2,8.0≤==e a b ，如果今年该地区财政收入10亿元，则年支出预计不会超过（ ）A.10亿元B.9亿元C.10.5亿元D.9.5亿元【知识点：回归模型，】解：C 点拨：带入数据，得,10e y +=∧又,5.0||≤e 得5.105.9≤≤∧y . 3.已知y x ,的值如下表所示，若y 与x 具有相关关系且其回归直线方程为,2741x y +=∧则a =( )A.4B.5C. 6D. 7【知识点：回归直线方程】解： A 点拨：又表格求得y x ,的值，带入回归直线方程，建立关于a 的方程求解. 4. 有下列关系：①人的年龄与他（她）拥有的财富之间的关系； ②曲线上的点与该点的坐标之间的关系； ③苹果的产量与气候之间的关系；④森林中的同一种树木，其横断面直径与高度之间的关系， ⑤学生他（她）的学号之间的关系.（填序号） 【知识点：函数关系，相关关系】 答案：①③④ 探究型 多维突破1.下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x （单位：吨）与相应的能耗y （单位：吨标准煤）的几组对照数据（1）请画出上表数据的散点图.（2）y 与x 是否具有线性相关关系？若是，则求出y 关于x 的线性回归方程.（3）已知该厂技术改造前100吨甲产品的生产能耗为90吨标准煤，试根据（2）中求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤（参考值：5.665.4645345.23=⨯+⨯+⨯+⨯） 【知识点：散点图，相关关系，回归分析】 解：（1）略（2）由散点图可知，各数据点大致分布在一条直线的附近，故具有线性相关关系.计算得86412=∑=i ix，5.6641=∑=i i i y x ，,5.3,5.4==y x 又最小二乘法确定的线性回归方程的参数为.35.0,7.0==∧∧a b 故所求的线性回归方程为35.07.0+=∧x y .（3）由（2）中的线性回归方程及技术改造前100吨甲产品的生产能耗，得降低的生产能耗为65.1935.01007.090=+⨯-）（（吨标准煤）. （四）自助餐1.下面列两个变量之间呈相关关系的是（ ） A.圆的面积与半径 B.球的体积与半径 C.角的度数与它的正切值D.一个考生的数学成绩与物理成绩 【知识点：相关关系】 解：D2.下列关于回归分析说法错误的是（ ） A.回归分析是研究两个具有相关关系的变量的方法 B.在散点图中，解释变量在x 轴，预报变量在y 轴 C.回归模型中一定存在随机误差 D.散点图能明确反映变量间的关系 【知识点：回归分析】 解：D3.已知变量x 与y 正相关，且由观测数据算得样本平均数5.3,3==y x ，由此该观测数据算得的线性回归方程可能是（ ） A.3.24.0+=∧x y B.4.2-2x y =∧ C.5.92-+=∧x y D.4.43.0-+=∧x y【知识点：回归方程，样本点中心】 解：A4.为了了解儿子身高与父亲身高的关系，随机抽取5对父子的身高数据如下则y 对于x 的线性回归方程为（ ）A.1+=∧x y B.1+=∧x y C.885.0+=∧x y D.12+=∧x y【知识点：回归方程】 解：C5.小李同学根据下表记录的产量x （吨）和能耗y （吨标准煤）对应的四组数据，用最小二乘法求出了y 对于x 的线性回归方程是070.35y x ∧=+.，之后不慎将一滴墨水滴于表内，表中第二行第四列的数据已经无法看清，据你判断这个数据应该是（ ）A.3.5B.3.75C. 4D. 4.25【知识点：回归方程，样本点中心】 解：C6.四名同学根据各自的样本数据研究变量x ，y 之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y 与x 负相关且623.0-347.2x y =∧；②y 与x 负相关且648.5476.3-+=∧x y ；③y 与x 正相关且493.8437.5+=∧x y ；④y 与x 正相关且578.4-326.4-x y =∧. 其中一定不正确的结论序号是（ ） A.①② B.②③ C.③④ D.①④【知识点：回归方程，正相关、负相关】 解：D7.若施化肥量x 与小麦产量y 之间的回归直线方程为x y 4250ˆ+=，当施化肥量为50kg 时，预计小麦产量为__________.解析：当50=x 时，450450250ˆ=⨯+=y . 答案：kg 450.8.年或者更少教育的百分比（x ）和收入低于官方规定的贫困线人数占本地区的人数的百分比（y ）的数据，建立的回归直线方程6.48.0+=∧x y ，斜率的估计值为0.8，说明__________;成年人受过9年或者更少教育的百分比（x ）与收入低于官方规定的贫困线的人数占本地区人数的百分比（y ）之间的相关系数__________（填“大于0”或“小于0”）. 【知识点：回归方程，回归分析】解：一个地区受过9年或者更少教育的百分比每增加1%，收入低于官方规定的贫困线的人数占本地区人数的百分比将增加0.8%左右 大于0.9.对具有线性相关关系的变量x ，y 有一组观测数据),8,,2,1)(, =i y x i i （其回归直线方程是a x y +=∧31，且,6)(2821821=+++=+++y y y x x x 则实数a 的值是__________. 【知识点：回归方程，回归分析】解：8110.某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：（1）求回归直线方程y bx a ∧=+，其中20-=b ，a y bx =-；（2）预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本) 【知识点：回归方程，相关关系，回归分析】解：(1)由于x ＝16(x 1＋x 2＋x 3＋x 4＋x 5＋x 6)＝8.5，y ＝16(y 1＋y 2＋y 3＋y 4＋y 5＋y 6)＝80，所以a ＝y －b x ＝80＋20×8.5＝250，从而回归直线方程为y ＝－20x ＋250. (2)设工厂获得的利润为L 元，依题意得L ＝x (－20x ＋250)－4(－20x ＋250)＝－20x 2＋330x －1 000＝－20(x－334)2＋361.25， 当且仅当x ＝8.25时，L 取得最大值.故当单价定为8.25元时，工厂可获得最大利润.11. 下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图（1）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； （2）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量. 参考数据：719.32i i y ==∑，7140.17i i i t y ==∑，()7210.55i i y y=-=∑，7≈2.646.参考公式：相关系数1221t)(y y)(t t)(y y)niii niii r ==--=--∑∑回归方程 中斜率和截距的最小二乘估计公式分别为： 121(t t)(y y)(t t)niii ni i b ∧==--=-∑∑，a y b t =-【知识点：回归方程，相关关系，回归分析】 解：（1）由折线图这数据和附注中参考数据得4=t ，28)(712=-∑=i i t t ，55.0)(712=-∑=i iy y，89.232.9417.40))((717171=⨯-=-=--∑∑∑===i i i iii i iy t yt y y t t，99.0646.2255.089.2≈⨯⨯≈r .因为y 与t 的相关系数近似为0.99，说明y 与t 的线性相关相当高，从而可以用线性回归模型拟合y 与t 的关系.（2）由9.321.3317y =≈及（1）得7121()()2.890.10328()iii ni i t t y y b t t ∧==--==≈-∑∑， 92.04103.0331.1ˆˆ≈⨯-≈-=t b y a .所以，y 关于t 的回归方程为：t y10.092.0ˆ+=. 将2016年对应的9=t 代入回归方程得：82.1910.092.0ˆ=⨯+=y. 所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.。