方程组不等式计算题过关训练基础版
- 格式:doc
- 大小:46.50 KB
- 文档页数:2

不等式练习题一、基本不等式1. 已知a > b,求证:a + c > b + c。
2. 已知x > 3,求证:x^2 > 9。
3. 已知0 < x < 1,求证:x^3 < x。
4. 已知a, b均为正数,求证:a^2 + b^2 > 2ab。
5. 已知|x| > |y|,求证:x^2 > y^2。
二、一元一次不等式1. 解不等式:3x 7 > 2x + 4。
2. 解不等式:5 2(x 3) ≤ 3x 1。
3. 解不等式:2(x 1) 3(x + 2) > 7。
4. 解不等式:4 3(x 2) ≥ 2x + 5。
5. 解不等式:5(x 3) + 2(2x + 1) < 7x 9。
三、一元二次不等式1. 解不等式:x^2 5x + 6 > 0。
2. 解不等式:2x^2 3x 2 < 0。
3. 解不等式:x^2 4x + 4 ≤ 0。
4. 解不等式:3x^2 + 4x 4 > 0。
5. 解不等式:x^2 + 5x 6 < 0。
四、分式不等式1. 解不等式:x / (x 1) > 2。
2. 解不等式:1 / (x + 3) 1 / (x 2) ≤ 0。
3. 解不等式:(x 1) / (x + 1) < 0。
4. 解不等式:(2x + 3) / (x 4) ≥ 1。
5. 解不等式:(3x 2) / (x^2 5x + 6) > 0。
五、含绝对值的不等式1. 解不等式:|x 2| > 3。
2. 解不等式:|2x + 1| ≤ 5。
3. 解不等式:|3x 4| < 2。
4. 解不等式:|x + 3| |x 2| > 1。
5. 解不等式:|x 5| + |x + 1| < 6。
六、综合应用题1. 已知不等式组:$\begin{cases} 2x 3y > 6 \\ x + 4y ≤ 8 \end{cases}$,求x的取值范围。

完整版)解不等式组计算专项练习60题(有答案)1.解不等式组60题参考答案:1.解:由不等式①得2a-3x+1≥0,即x≤(2a+1)/3;由不等式②得3b-2x-16≥0,即x≤(3b-16)/2.又因为a≤4<b,所以2a+1≤9,3b-16≥8,所以x的取值范围为x≤3或x≥-11/2.2.解:由不等式①得x≤-1或x≥3;由不等式②得x≤4/3或x≥2.综合起来,x的取值范围为x≤-1或x≥3,或者4/3≤x≤2.3.解:由不等式①得x>(a+1)/2;由不等式②得x0,所以a/2>(a+1)/2,所以不等式组的解集为a/2<x<(a+1)/2.4.解:由不等式①得x≥1;由不等式②得x<3.所以不等式组的解集为1≤x<3.5.解:由不等式①得x≤-2;由不等式②得x>-3.所以不等式组的解集为-3<x≤-2.6.解:由不等式①得x>-1;由不等式②得x≤2.所以不等式组的解集为-1<x≤2.7.解:由不等式①得x≤-1;由不等式②得x≥-2.所以不等式组的解集为-2≤x≤-1.8.解:由不等式①得x>-3;由不等式②得x≤1.所以不等式组的解集为-3<x≤1.9.解:由不等式①得x>-1;由不等式②得x≤4.所以不等式组的解集为-1<x≤4.10.解:由不等式①得x-3.所以不等式组的解集为-3<x<2.11.解:由不等式①得x≥1;由不等式②得x<3.所以不等式组的解集为1≤x<3.1.由不等式组的①得x≥-1,由不等式组的②得 x<4,因此不等式组的解集为 -1≤x<4.2.由不等式①得x≤3,由不等式②得 x>0,因此不等式组的解集为0<x≤3.3.解不等式①得x≥1,解不等式②得 x<4,因此不等式组的解集为1≤x<4.4.原不等式组可化为:x+45,x<-1.因此不等式组的解集为-3<x≤3.5.解不等式①得 x<5,解不等式②得x≥-2,因此不等式组的解集为 -2≤x<5.6.解不等式①得x≥1,解不等式②得 x<4,因此不等式组的解集为1≤x<4.7.解不等式①得x≥-1,解不等式②得 x<3,因此不等式组的解集为 -1≤x<3.8.解不等式①得 x<1,解不等式②得x≥-2,因此不等式组的解集为 -2≤x<1.9.解不等式①得 x>-1,解不等式②得x≤4,因此不等式组的解集为 -1<x≤4.10.解不等式①得x≥1,解不等式②得 x<4,因此不等式组的解集为1≤x<4.11.解不等式①得 x>-1,解不等式②得x≤4,因此不等式组的解集为 -1<x≤4.12.解不等式组的①得-∞<x<1,因为②中的不等式没有解,所以不等式组的解集为 -∞<x<1.13.解不等式①得x≥1,解不等式②得 x<4,因此不等式组的解集为1≤x<4.14.原不等式组可化为:x>-3,x≤3.因此不等式组的解集为-3<x≤3.15.解不等式组的①得 x<1,因为②中的不等式没有解,所以不等式组的解集为 -∞<x<1.16.解不等式①得 x<2,解不等式②得x≥-1,因此不等式组的解集为 -1≤x<2.17.解不等式①得x≥1,解不等式②得1≤x<4,因此不等式组的解集为1≤x<4.18.解不等式①得x≥-1,解不等式②得 x<3,因此不等式组的解集为 -1≤x<3.19.解不等式①得 x<1,解不等式②得x≥-2,因此不等式组的解集为 -2≤x<1.20.解不等式①得 x>-1,解不等式②得x≤4,因此不等式组的解集为 -1<x≤4.21.不等式①的解集为x≥1,不等式②的解集为 x<4,因此原不等式的解集为1≤x<4.22.解不等式①得 x<0,解不等式②得x≥3,因此原不等式无解。

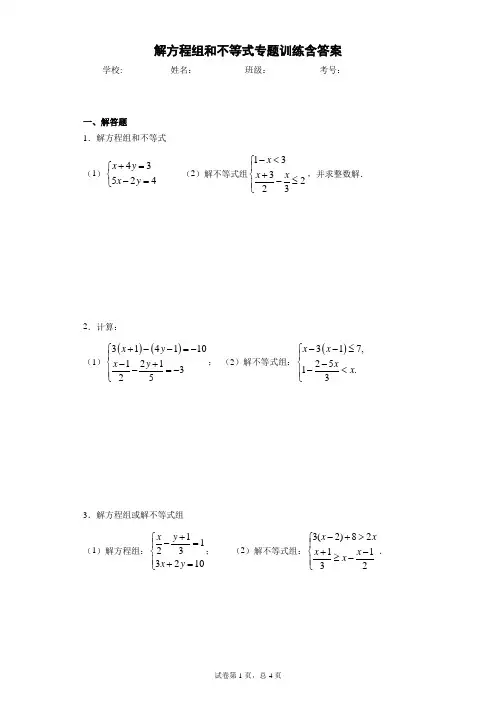
解方程组和不等式专题训练含答案学校:___________姓名:___________班级:___________考号:___________一、解答题1.解方程组和不等式(1)43524x yx y+=⎧⎨-=⎩(2)解不等式组133223xx x-<⎧⎪+⎨-≤⎪⎩,并求整数解.2.计算:(1)()()314110121325x yx y⎧+--=-⎪⎨-+-=-⎪⎩;(2)解不等式组:()317,251.3x xxx⎧--≤⎪⎨--<⎪⎩3.解方程组或解不等式组(1)解方程组:11233210x yx y+⎧-=⎪⎨⎪+=⎩;(2)解不等式组:3(2)821132x xx xx-+>⎧⎪+-⎨≥-⎪⎩.4.(12-(2)解方程组:3(1)51135x yy x-=+⎧⎪-⎨=+⎪⎩(3)解不等式组3(2)41213x xxx--≤-⎧⎪+⎨>-⎪⎩,并写出该不等式组的整数解.5.解下列方程(不等式)组.(1)解方程组:2332 x yx y-=⎧⎨+=-⎩(2) 解不等式组:23(2)421152x xx x--≥⎧⎪-+⎨<⎪⎩,并求其非负整数解.6.解方程组或不等式组:(1)解方程组:231324x yx y+=⎧⎨-=-⎩(2)解不等式组:3511343xxx-≤⎧⎪-⎨<⎪⎩7.解方程组或不等式组:(1)解方程组:524235x yx y-=⎧⎨-=-⎩;(2)解不等式组:121312x xx-≥⎧⎪⎨+≤-⎪⎩8.解方程组或不等式组(1)解方程组143xyx y⎧-=-⎪⎨⎪=⎩(2)解不等式组321351x xx+≥-⎧⎨-≥⎩.9.解方程组和不等式组:(1)解方程组:125x yx y+=⎧⎨-=⎩①②;(2)解不等式组121213xxx+≤⎧⎪+⎨>-⎪⎩.10.解方程组或不等式组(1)解方程组104()5x yx y y--=⎧⎨--=⎩(2)解不等式组()2233123x xx x⎧-≤-⎪⎨+<⎪⎩11.(1)解方程组:4421x yx y-=⎧⎨+=-⎩;(2)解不等式组:13(1)83312x xxx--<-⎧⎪⎨-+≥+⎪⎩.参考答案1.(1)10.5xy=⎧⎨=⎩;(2)-2<x≤3;-1,0,1,2,3【解析】【分析】(1)利用加减消元法解方程组即可解答;(2)先分别求出两个不等式的解集,再求出两个解集的公共部分即为不等式组的解集,然后从中找出整数解即可.【详解】(1)43524x yx y+=⎧⎨-=⎩①②,①+②×2得:11x=11,解得:x=1,将x=1代入①中得:1+4y=3,解得:y=0.5,所以原方程组的解为10.5 xy=⎧⎨=⎩;(2)133223xx x-<⎧⎪⎨+-≤⎪⎩①②,解①得:x﹥﹣2,解②得:x ≤ 3,∴不等式组的解集为-2﹤x ≤ 3,且整数解为-1,0,1,2,3.【点睛】本题考查了解一元一次方程组、解一元一次不等式组及整数解,属于基础题型,必须熟练掌握.2.(1)9218xy⎧=-⎪⎪⎨⎪=⎪⎩;(2)122x-≤<-【解析】本卷由系统自动生成,请仔细校对后使用,答案仅供参考。

初中数学关于方程与不等式综合训练题在初中数学的学习中,方程与不等式是非常重要的知识点,它们不仅在数学学科中有着广泛的应用,也为我们解决实际问题提供了有力的工具。
今天,让我们一起来进行一次方程与不等式的综合训练,通过各种类型的题目,加深对这两个知识点的理解和掌握。
一、一元一次方程一元一次方程是方程中最基础的类型,形如$ax + b = 0$(其中$a$、$b$为常数,且$a ≠ 0$)。
例 1:若关于$x$的方程$2x + 3 = 5$,则$x =$_____。
解:移项可得$2x = 5 3$,即$2x = 2$,解得$x = 1$。
一元一次方程的解题关键在于通过移项、合并同类项等操作,将方程化为$x =$常数的形式。
练习 1:解方程$3x 5 = 7$。
解:移项得$3x = 7 + 5$,即$3x = 12$,解得$x = 4$。
二、二元一次方程组二元一次方程组是由两个含有两个未知数的一次方程组成的方程组,一般形式为$\begin{cases}ax + by = c\\dx + ey = f\end{cases}$。
例 2:解方程组$\begin{cases}2x + y = 5\\x y = 1\end{cases}$解:将两式相加,可得$3x = 6$,解得$x = 2$。
将$x = 2$代入$x y = 1$,可得$2 y = 1$,解得$y = 1$。
解二元一次方程组的常用方法有代入消元法和加减消元法。
练习 2:解方程组$\begin{cases}3x + 2y = 8\\2x y =3\end{cases}$解:由$2x y = 3$可得$y = 2x 3$,将其代入$3x + 2y = 8$,可得$3x + 2(2x 3) = 8$,解得$x = 2$。
将$x = 2$代入$y = 2x 3$,可得$y = 1$。
三、一元二次方程一元二次方程的一般形式为$ax^2 + bx + c = 0$(其中$a$、$b$、$c$为常数,且$a ≠ 0$)。

基本不等式A 级——基础过关练1.下列不等式中,正确的是( ) A .a +4a≥4B .a 2+b 2≥4abC .ab ≥a +b2D .x 2+3x2≥2 3【答案】D 【解析】a <0,则a +4a≥4不成立,故A 错;a =1,b =1,a 2+b 2<4ab ,故B 错;a =4,b =16,则ab <a +b2,故C 错;由基本不等式可知D 项正确.2.(2021年哈尔滨期末)“a >b >0”是“ab <a 2+b 22”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A 【解析】由a >b >0得a 2+b 2>2ab ;但由a 2+b 2>2ab 不能得到a >b >0.故“a >b >0”是“ab <a 2+b 22”的充分不必要条件.3.(2020年白银高一期中)当x ≥3时,x +4x -1的最小值为( ) A .5 B .4 C .112D .163【答案】A 【解析】x +4x -1=x -1+4x -1+1,令t =x -1,∵x ≥3,所以t ≥2,所以原式y =t +4t +1≥5,当且仅当t =2时等号成立,所以x +4x -1≥5.故选A .4.(多选)已知实数a ,b ,判断下列不等式中哪些一定是正确的( ) A .a +b2≥abB .a +1a≥2C .⎪⎪⎪⎪⎪⎪a b +ba ≥2 D .2(a 2+b 2)≥(a +b )2【答案】CD 【解析】当a <0,b <0时,a +b2≥ab 不成立;当a <0,时,a +1a≥2不成立;因为⎪⎪⎪⎪⎪⎪a b +b a =⎪⎪⎪⎪⎪⎪a b +⎪⎪⎪⎪⎪⎪b a ≥2,故C 正确;因为2(a 2+b 2)-(a +b )2=a 2+b 2-2ab =(a -b )2≥0,所以2(a 2+b 2)≥(a +b )2,故D 正确.故选CD .5.(2021年宝鸡模拟)设x >0,y >0且x +4y =40,则xy 的最大值是( ) A .10 B .40 C .100D .400【答案】C 【解析】因为x >0,y >0且x +4y =40,所以x +4y ≥2x ·4y =4xy ,当且仅当x =4y 时取“=”.所以4xy ≤40,得xy ≤100.6.要制作一个容积为4 m 3,高为1 m 的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是________元.【答案】160 【解析】设底面矩形的一边长为x ,由容器的容积为4 m 3,高为1 m ,得另一边长为4xm .记容器的总造价为y 元,则y =4×20+2⎝ ⎛⎭⎪⎫x +4x ×1×10=80+20⎝ ⎛⎭⎪⎫x +4x ≥80+20×2x ·4x =160,当且仅当x =4x,即x =2时,等号成立.因此当x =2时,y 取得最小值160,即容器的最低总造价为160元.7.3-aa +6(-6≤a ≤3)的最大值为________.【答案】92 【解析】因为-6≤a ≤3,所以3-a ≥0,a +6≥0,则由基本不等式可知3-aa +6≤3-a +a +62=92,当且仅当a =-32时等号成立.8.已知x >0,y >0,2x +3y =6,则xy 的最大值为________.【答案】32 【解析】因为x >0,y >0,2x +3y =6,所以xy =16(2x ·3y )≤16⎝ ⎛⎭⎪⎫2x +3y 22=16×⎝ ⎛⎭⎪⎫622=32,当且仅当2x =3y 且2x +3y =6,即x =32,y =1时等号成立,xy 取到最大值32.9.设a ,b ,c 都是正数,求证:b +c a +c +a b +a +bc ≥6. 证明:因为a >0,b >0,c >0,所以b a +a b≥2,c a +a c≥2,c b +b c≥2.所以⎝ ⎛⎭⎪⎫b a +a b +⎝ ⎛⎭⎪⎫c a +a c +⎝ ⎛⎭⎪⎫c b +b c ≥6,当且仅当b a =a b ,c a =a c ,c b =b c,即a =b =c 时等号成立.所以b +c a +c +a b +a +bc≥6. B 级——能力提升练10.若0<x <12,则x 1-4x 2的最大值为( )A .1B .12C .14D .18【答案】C 【解析】因为0<x <12,所以1-4x 2>0,所以x 1-4x 2=12×2x ×1-4x 2≤12×4x 2+1-4x 22=14,当且仅当2x =1-4x 2,即x =24时等号成立.故选C .11.已知x ≥52,则x 2-4x +52x -4有( )A .最大值54B .最小值54C .最大值1D .最小值1【答案】D 【解析】x 2-4x +52x -4=x -22+12x -2=12⎣⎢⎡⎦⎥⎤x -2+1x -2.因为x ≥52,所以x -2>0,所以12⎣⎢⎡⎦⎥⎤x -2+1x -2≥12·2 x -2·1x -2=1,当且仅当x -2=1x -2,即x =3时取等号.故原式有最小值为1.12.已知不等式(x +y )⎝ ⎛⎭⎪⎫1x +a y ≥9对任意正实数x ,y 恒成立,则正实数a 的最小值为( )A .2B .4C .6D .8【答案】B 【解析】不等式(x +y )⎝ ⎛⎭⎪⎫1x +a y ≥9对任意正实数x ,y 恒成立,则(x +y )⎝ ⎛⎭⎪⎫1x +a y =1+a +ax y +yx ≥1+a +2ax y ·y x=1+a +2a =(1+a )2≥9,所以a ≥2,即a ≥4,故正实数a 的最小值为4.13.设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0,则当xy z取得最大值时,2x +1y -2z的最大值是________.【答案】1 【解析】xy z =xy x 2-3xy +4y 2=1x y +4y x-3≤14-3=1,当且仅当x =2y 时等号成立,此时z =2y 2,2x +1y -2z=-1y2+2y=-⎝ ⎛⎭⎪⎫1y -12+1≤1,当且仅当y =1时等号成立,故所求的最大值为1.14.已知a ,b 均为正数,且a +b +3=ab ,则ab 的最小值是________,a +b 的最小值是________.【答案】9 6 【解析】①由题意可得a +b =ab -3≥2ab ,所以ab ≥3,所以ab ≥9,当且仅当a =b =3时取等号,所以ab 的最小值为9;②a +b +3=ab ≤⎝ ⎛⎭⎪⎫a +b 22,所以a +b ≥6,当且仅当a =b =3时取等号,所以a +b 的最小值为6.15.(2021年株洲期中)某村计划建造一个室内面积为800 m 2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1 m 宽的通道,沿前侧内墙保留3 m 宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?解:设矩形温室的左侧边长为a m ,后侧边长为b m , 则ab =800.蔬菜的种植面积S =(a -4)(b -2)=808-2(a +2b ).S ≤808-42ab =648(m 2),当且仅当a =2b ,即a =40 m ,b =20 m 时,S 最大值=648 m 2.所以当矩形温室的左侧边长为40 m ,后侧边长为20 m 时,蔬菜的种植面积最大,最大种植面积为648 m 2.C 级——探究创新练16.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F 在半圆O 上,点C 在直径AB 上,且OF ⊥AB ,设AC =a ,BC =b ,则该图形可以完成的无字证明为( )A .a +b2≥ab (a >b >0)B .a 2+b 2≥2ab (a >b >0) C .2aba +b≤ab (a >b >0) D .a +b2≤a 2+b 22(a >b >0)【答案】D 【解析】由图形可知OF =12AB =12(a +b ),OC =12(a +b )-b =12(a -b ).在Rt △OCF 中,由勾股定理得CF =⎝ ⎛⎭⎪⎫a +b 22+⎝ ⎛⎭⎪⎫a -b 22=12a 2+b 2.因为CF ≥OF ,所以1 2a2+b2≥12(a+b)(a>b>0).故选D.。

【中考数学总复习一轮】不等式与不等式组(方程与不等式)基础练习一、填空题(共3道,每道20分)1.不等式的基本性质:①不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向________;②不等式的两边都乘以(或除以)同一个正数,不等号的方向________;③不等号的两边都乘以(或除以)同一个负数,不等号的方向_________.答案:不变;不变;相反解题思路:直接应用不等式的性质即可试题难度:三颗星知识点:不等式的性质2.已知方程组的解x、y满足2x+y≥0,则m的取值范围是.答案:解题思路:由方程组,得,代入2x+y=0,得试题难度:三颗星知识点:解一元一次不等式3.已知关于的不等式组只有四个整数解,则实数的取值范围是;答案:解题思路:解不等式组得到x,有四个整数解,则为1,0,-1,-2.所以试题难度:三颗星知识点:解一元一次不等式组二、解答题(共2道,每道20分)1.今年四月份,李大叔收获洋葱30吨,黄瓜13吨,现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨;一辆乙种货车可装洋葱和黄瓜各2吨.(1)李大叔安排甲、乙两种货车时有几种方案?请你帮助设计出来;(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,请帮李大叔算一算应选择哪种方案,才能使运费最少?最少运费是多少元?答案:(1)运货方案一为用甲种车5辆,乙种车5辆运货方案二为用甲种车6辆,乙种车4辆运货方案三为用甲种车7辆,乙种车3辆(2)16500元解题思路:(1)设用甲种货车x辆,则用乙种货车(10-x)辆,依题意,且x正整数。
解得,所以x取5,6,7则运货方案一为用甲种车5辆,乙种车5辆运货;方案二为用甲种车6辆,乙种车4辆运货;方案三为用甲种车7辆,乙种车3辆(2)需付车费用为2000x+1300(10-x)=13000+700x费用关于x是增函数,则选择第一种方案费用最低,最低为13000+700=16500元试题难度:三颗星知识点:一元一次不等式组的应用2.某校组织七年级学生到军营训练,为了喝水方便,要求每个学生各带一只水杯,几个学生可以合带一个水壶.可临出发前,带队老师发现有51名同学没带水壶和水杯,于是老师拿出260元钱并派两名同学去附近商店购买.该商店有大小不同的甲、乙两种水壶,并且水壶与水杯必须配套购买.每个甲种水壶配4只杯子,每套20元;每个乙种水壶配6只杯子,每套28元.若需购买水壶10个,设购买甲种水壶x个,购买的总费用为y(元).(1)求出y与x之间的函数关系式(不必写出自变量x的取值范围);(2)请你帮助设计所有可能的购买方案,并写出最省钱的购买方案及最少费用.答案:(1)(2)248元解题思路:(1)(2)依题意列方程,且x取正整数,解得,所以x取3,4则方案一购买甲种水壶3个,购买乙种水壶7个;方案二购买甲种水壶4个,购买乙种水壶6个.由于费用关于x为减函数,则取x为4时费用最少最省钱,即方案一最省钱,最少费用为(元)试题难度:三颗星知识点:一元一次不等式组的应用。

1、若实数x ,y 满足224x y +=,求xy 的最大值
2、若x>0,求9()4f x x x =+
的最小值;
3、若0x <,求1y x x =+
的最大值
4、若x<0,求9()4f x x x =+
的最大值
5、求9()45
f x x x =+
-(x>5)的最小值.
6、若x ,y R +∈,x+y=5,求xy 的最值
7、若x ,y R +∈,2x+y=5,求xy 的最值
8、已知直角三角形的面积为4平方厘米,求该三角形周长的最小值
1、求1 (3)3y x x x =
+>-的最小值.
2、求(5) (05)y x x x =-<<的最大值.
3、求1(14)(0)4y x x x =-<<的最大值。
4、求123 (0)y x x x =
+<的最大值.
5、若2x >,求1252y x x =-+
-的最小值
6、若0x <,求21x x y x ++=
的最大值。
7、求2
y =
的最小值.
8(1)用篱笆围成一个面积为100m 2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。
最短的篱笆是多少?
(2)段长为36 m 的篱笆围成一个一边靠墙的矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?。

1、解方程(组)1、213x -= 24x +-12、0)12(2)5(5=---x x3、⎩⎨⎧=+=-2451443y x y x4、⎩⎨⎧=-+=+-;010073,0203y x y x5、2x x --1= 214x - 6、6x 2-x -12 =0(配方法)7、x 2-4x -1=0(公式法) 8、2x 2-5x -3=0(因式分解法)5. 方程组23112x y kx k y +=+-=⎧⎨⎩(),x 与y 的值相等,求k 的值?1、当x= 时,代数式3x -5与1-2x 的值互为相反数;当x= 时,代数式3x -5与1-2x 的值相等;当x= 时,代数式3x -5与1-2x 的值大4.2、在2x -3y=6中,用含x 的代数式表示y 的结果是 ,用含y 的代数式表示x 的结果是 3.若mxy 十9x 十3yn-1=7是关于x ,y 的二元一次方程,则m 十n=()A. 0B. 1C. 2 D 34.若x=2是关于x 的方程2x+3k-1=0的解,则k 的值是________.5.方程组⎩⎨⎧=-=+7211y x y x 的解是__________.6.分式方程131x x x x +=--的解为( ) A .1x =B .1x =-C .3x =D .3x =-7.22___)(_____8+=++x x x 22____)(_____4-=+-x x x8、方程 0)2)(1(=-+x x 的根是 ;方程0162=-x 的根是 ;方程x 2-x =0的根是 9.方程032=-x 的根是( )(A )3=x (B )3,321-==x x (C )3=x (D )3,321-==x x 10.关于x 的一元二次方程02)32(2=-+--a x a x 根的情况是( ) A .有两个相等的实数根 B. 没有实数根C. 有两个不相等的实数根 C. 根的情况无法确定 11、关于x 的方程0132=-+x kx 有实数根,则K 的取值范围是( ) A 、49-≤k B 、0k 49≠-≥且k C 、49k -≥ D 、0k 49k ≠->且 12.一元二次方程220x x +-=的两根之积是( ) A .-1 B .-2 C .1 D .2 13. 用配方法或公式法解下列方程.:(1)x 2+ 2x + 3=0 (2) x 2-2x -1 =0 (3) 7x 2-4x -3 =0 (4) -x 2-x+12 =01.不等式组⎪⎩⎪⎨⎧-≥>+32132x x x x 的解集是2.不等式组⎩⎨⎧>>-121x x 的解集是( )A.B.C.D.3.把不等式2x -< 4( )4.一个一元一次不等式组的解集在数轴上的表示如下图,则该不等式组的解集是( )A .13x -≤< B . 13x -<≤ C .1x ≥- D . 3x <5.把不等式组110x x +⎧⎨-≤⎩>0,的解集表示在数轴上,如下图,正确的是()A B C D6.已知点P (a -1,a +2)在平面直角坐标系的第二象限内,则a 的取值范围在数轴上可表示为( )7、关于x 的方程3x -m =5+2(2m -x )的解为正数,求m 的取值范围。

第二讲:方程与不等式第一关:考点点睛一元一次方程考点一方程解的应用例1(2009·芜湖)已知方程3x2x-9x+m=0的一个根是1,则m的值是。
解题思路:根据方程解的定义,把方程的解x=1代入方程成立,然后解决关于m的方程即可,解:把x=1代入原方程,得3×21-9×1+m=0,解得m=6 答案:6点评:解题依据是方程解的定义,解题方法是把方程的解代入原方程,转化为关于待定系数的方程。
考点二巧解一元一次方程例2(2008·江苏)解方程:341138 43242x x ⎡⎤⎛⎫--=⎪⎢⎥⎝⎭⎣⎦解题思路:此题先用分配律简化方程,再解就容易了。
解:去括号,得1136242x x--=移项、合并同类项,得-x=614,系数化为1,得x=-614点评:解一元一次方程,掌握步骤,注意观察特点,寻找解题技巧,灵活运用分配委或分数基本性质等,使方程简化。
考点三根据方程ax=b解的情况,求待定系数的值例3已知关于x的方程1(6)326x xa x+=--无解,则a的值是()A.1B.-1C.±1D.不等于1的数解题思路:需先化成最简形式,再根据无解的条件,列出a的等式或不等式,从而求出a的值。
解:去分母,得2x+6a=3x-x+6,即0·x=6-6a因为原方程无解,所以有6-6a≠0,即a≠1,答案:D考点四一元一次方程的应用例4(2009·福州)某班学生为希望工程共捐款131元,比每人平均2 元还多35元,设这个班的学生有x 人,根据题意列方程为_________________。
解题思路:本题的相等关系是捐款总数相等,解决此题的关键是用学生人数、平均数与余数35元表示出捐款总数(2x+35)元。
答案:2x+35=131二元一次方程考点1:二元一次方程及其解例1:下列方程中,是二元一次方程的是()A.3x-2y=4z B.6xy+9=0 C.1x+4y=6 D.4x=24y-思路点拨:掌握判断二元一次方程的三个必需条件:①含有两个未知数;②含有未知数的项的次数是1;③等式两边都是整式.所以选D例2:二元一次方程5a-11b=21 ()A.有且只有一解B.有无数解C.无解D.有且只有两解思路点拨:不加限制条件时,一个二元一次方程有无数个解.所以选B考点2:二元一次方程组及其解例1:下列方程组中,是二元一次方程组的是()A.228 423119 (23754624)x yx y a b xB C Dx y b c y x x y+= +=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩思路点拨:二元一次方程组的三个必需条件:①含有两个未知数,②每个含未知数的项次数为1;③每个方程都是整式方程.所以选A例2:已知│x-1│+(2y+1)2=0,且2x-ky=4,则k=_____.思路点拨:由已知得x -1=0,2y+1=0,∴x=1,y=-12,把112x y =⎧⎪⎨=-⎪⎩代入方程2x -ky=4中,2+12k=4,∴k=1. 考点3:二元一次方程组的应用例1”捐款,共捐款100元.捐款情况如表:47表格中捐款2若设捐款2元的有x 名同学,捐款3元的有y 名同学,根据题意,可得方程组( )A.⎩⎨⎧=+=+663227y x y xB.⎩⎨⎧=+=+1003227y x y xC.⎩⎨⎧=+=+662327y x y xD.⎩⎨⎧=+=+1002327y x y x 思路点拨:这是一道表格信息题,通过已知条件可发现两个等量关系:总人数为40人,总捐款金额100元.利用表格信息可列方程组⎩⎨⎧=+=+663227y x y x ,故应选A .例2 :如图,点O 在直线AB 上,OC 为射线,1∠比2∠的3倍少︒10,设1∠,2∠的度数分别为x ,y ,那么下列求出这两个角的度数的方程是( )A.⎩⎨⎧-==+10180y x y xB.⎩⎨⎧-==+103180y x y x C.⎩⎨⎧+==+10180y x y x D.⎩⎨⎧-==1031803y x y思路点拨:本题侧重考查学生的数形结合思想.已知条件看似给了一个,其实还有一个隐含条件,即1∠与2∠互为邻补角.利用它们可列方程组⎩⎨⎧-==+103180y x y x ,故应选B .分式方程考点1:分式的定义例1:请从下列三个代数式中任选两个构成一个分式,并化简该分式x2-4xy+4y2x2-4y2x-2yA .1 B. 2 C.3 D.4 思路点拨:分母中含字母的代数式,xy x 1,2-都是分式,其他都不是。

初中数学一元一次不等式(组)单元综合基础过关训练题3(附答案)1.若 m >n ,则下列不等式中一定成立的是( )A .m +a <n +aB .ma <naC .a -m <a -nD .ma 2>na 22.若m n <,则下列各式正确的是( )A .55m n ->-B .2233m n >C .44m n ->-D .2525m n ->- 3.定义a bc d =ad ﹣bc ,例如:1234-=1×4﹣(﹣3)×2=10,若121x xx x -++≥7,则非负整数x 的值有( )A .5个B .4个C .3个D .0个 4.不等式的解集在数轴上表示正确的是( ) A .B .C .D .5.不等式组2220x x >⎧⎨-⎩的解在数轴上表示为( ) A .B .C .D .6.不等式组123x x -<⎧⎨-<⎩的解集是( ) A .x >﹣1B .x <5C .﹣1<x <5D .x <﹣1或x <5 7.不等式组2342x x x >⎧⎨+>⎩的整数解是( ) A .0 B .1- C .2- D .18.小明和爸爸、妈妈三人玩跷跷板.三人的体重一共为150千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端.这时爸爸那端仍然着地,那么小明的体重应小于( )A .49千克B .50千克C .24千克D .25千克9.不等式组213(1)14x x +>⎧⎨--≥⎩的最小整数解为( )A .x 0=B .x 1=-C .x 1=D .x 2=10.已知关于的不等式组的解集中任意一个的值均不在...的范围内,则的取值范围是( )A . 或B .C .D . 或 11.在下列所表示的不等式的解集中,不包括–5的是( )A .x ≤–4B .x ≥–5C .x ≤–6D .x ≥–7 12.若不等式组5512x x x m ++⎧⎨-⎩<>的解集是x >1,则m 的取值范围是___________ 13.若数a 使关于x 的不等式组x 11x 235x 2x a-+⎧<⎪⎨⎪-≥+⎩有且只有四个整数解,且使关于y 的方程y a 2a 2y 11y++=--的解为非负数,则符合条件的正整数a 的值为______. 14.关于x 的不等式2x ﹣a ≤﹣1的解集如图所示,则a 的取值范围是___.15.小宏准备用50元钱购买甲、乙两种饮料共10瓶.已知甲饮料每瓶7元,乙饮料每瓶4元,求小宏最多能买几瓶甲饮料.如果设小宏能买x 瓶甲饮料,那么根据题意所列的不等式应为_____.16.不等式2x+5≤12的正整数解是___________17.已知:y 1=2-3x ,y 2=x-6,当_________时,y 1≥y 2;18.已知0, 0a b <<,且a b <,那么ab ________b 2(填“>”“<”“=”). 19.若关于x 的分式方程3133x m x -=-的解为正数,则m 的取值范围是_____. 20.当m >-2时,关于x 的不等式(m +2)x >m +2的解集为______.21.式子1-22x -的值不大于1+33x 的值,那么x 的取值范围是___. 22.12?34x x ⎧+≥⎪⎨⎪<⎩的最大整数解是______.23.定义:对于实数a ,符号[]a 表示不大于a 的最大整数.例如:[]5.75=,[]55=,[]4π-=-.如果132x +⎡⎤=⎢⎥⎣⎦,则满足条件的所有正整数x 的值是______. 24.如图,长青农产品加工厂与 A ,B 两地有公路、铁路相连.这家工厂从 A 地购买一批原料甲运回工厂,经过加工后制成产品乙运到 B 地,其中原料甲和产品乙的重量都是正整数.已知铁路运价为 2 元/(吨·千米),公路运价为 8 元/(吨·千米).(1)若由 A 到 B 的两次运输中,原料甲比产品乙多 9 吨,工厂计划支出铁路运费超 过 5700 元,公路运费不超过 9680 元.问购买原料甲有哪几种方案,分别是多少吨? (2)由于国家出台惠农政策,对运输农产品的车辆免收高速通行费,并给予一定的 财政补贴,综合惠农政策后公路运输价格下降 m ( 0 < m < 4 且 m 为整数)元, 若由 A 到 B 的两次运输中,铁路运费为 5760 元,公路运费为 5100 元,求 m 的 值.25.对于给定的两个“函数,任取自变量x 的一个值,当x<1时,它们对应的函数值互为相反数;当x≥1时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x-4,它的相关函数为()()4141x x y x x ⎧-+⎪=⎨-≥⎪⎩<. (1)一次函数y = -x +5的相关函数为______________.(2)已知点A(b-1,4),点B 坐标(b +3,4),函数y =3x-2的相关函数与线段AB 有且只有一个交点,求b 的取值范围.(3)当b +1≤x ≤b +2时,函数y=-3x+b-2的相关函数的最小值为3,求b 的值.26.解不等式组,并在数轴上表示它们的解集.26321054x x x x -<⎧⎪+-⎨-≥⎪⎩ 27.某工厂计划生产A ,B 两种产品共10件,其中A 种产品的生产成本为每件3万元,B 种产品的生产成本为每件5万元;并且销售一件A 种产品的利润为1万元,销售一件B 种产品的利润为2万元。
方程与不等式之不等式与不等式组基础测试题附答案解析一、选择题1.不等式组30213x x +⎧⎨->⎩…的解集为( ) A .x >1B .x≥3C .x≥﹣3D .x >2【答案】D【解析】【分析】分别求出各不等式的解集,再求出其公共解集即可.【详解】 解:30213x x +>⎧⎨->⎩①②, 由①得,x ≥﹣3,由②得,x >2,故此不等式组的解集为:x>2.故选:D .【点睛】本题考查了解一元一次不等式组,解题的关键是分别解出各不等式的解集,利用数轴求出不等式组的解集,难度适中.2.某商品的标价比成本价高%a ,根据市场需要,该商品需降价%b .为了不亏本,b 应满足( )A .b a ≤B .100100a b a ≤+C .100a b a ≤+D .100100a b a ≤- 【答案】B【解析】【分析】根据最大的降价率即是保证售价大于等于成本价,进而得出不等式即可.【详解】解:设成本为x 元,由题意可得:()()1%1%x a b x +-?,整理得:100100b ab a +?, ∴100100a b a≤+, 故选:B .【点睛】 此题主要考查了一元一次不等式的应用,得出正确的不等关系是解题关键.3.关于 x 的不等式组21231xx a-⎧<⎪⎨⎪-+>⎩恰好只有 4 个整数解,则 a 的取值范围为()A.-2≤a<-1 B.-2<a≤-1 C.-3≤a<-2 D.-3<a≤-2【答案】A【解析】【分析】首先确定不等式组的解集,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a的不等式,从而求出a的范围.【详解】解:21231xx a-⎧<⎪⎨⎪-+>⎩①②解不等式组①,得x<72,解不等式组②,得x>a+1,则不等式组的解集是a+1<x<72,因为不等式组只有4个整数解,则这4个解是0,1,2,3.所以可以得到-1⩽ a+1<0,解得−2≤a<−1.故选A.【点睛】本题主要考查了一元一次不等组的整数解.正确解出不等式组的解集,确定a+1的范围,是解决本题的关键.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.4.不等式的解集在数轴上表示正确的是()A.B.C.D.【答案】C【解析】【分析】先解不等式,根据解集确定数轴的正确表示方法.【详解】解:不等式2x+1>-3,移项,得2x >-1-3,合并,得2x >-4,化系数为1,得x >-2.故选C .【点睛】本题考查解一元一次不等式,注意不等式的性质的应用.5.已知方程组31331x y m x y m +=+⎧⎨+=-⎩的解满足0x y +>,则m 取值范围是( ) A .m >1B .m <-1C .m >-1D .m <1 【答案】C【解析】【分析】 直接把两个方程相加,得到12m x y ++=,然后结合0x y +>,即可求出m 的取值范围. 【详解】解:31331x y m x y m+=+⎧⎨+=-⎩, 直接把两个方程相加,得:4422x y m +=+, ∴12m x y ++=, ∵0x y +>, ∴102m +>, ∴1m >-;故选:C.【点睛】 本题考查了加减消元法解方程组,解题的关键是掌握解方程组的方法,正确得到12m x y ++=,然后进行解题.6.不等式组360420x x +≥⎧⎨->⎩的所有整数解的和为( )A .1B .1-C .2D .2-【答案】D【解析】【分析】 求出不等式组的解集,再把所有整数解相加即可.【详解】360420x x +≥⎧⎨->⎩360x +≥解得2x ≥-420x ->解得2x >∴不等式组的解集为22x -≤<∴不等式组的所有整数解为2,1,0,1--∴不等式组的所有整数解之和为21012--++=-故答案为:D .【点睛】本题考查了解不等式组的问题,掌握解不等式组的方法是解题的关键.7.不等式组2201x x +>⎧⎨-≥-⎩的解在数轴上表示为( ) A .B .C .D .【答案】D【解析】【分析】解不等式组求得不等式组的解集,再把其表示在数轴上即可解答.【详解】 2201x x ①②+>⎧⎨-≥-⎩, 解不等式①得,x >-1;解不等式②得,x ≤1;∴不等式组的解集是﹣1<x ≤1.不等式组的解集在数轴上表示为:故选D.【点睛】本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解决问题的关键.8.不等式组13xx-≤⎧⎨<⎩的解集在数轴上可以表示为()A.B.C.D.【答案】B【解析】【分析】分别解不等式组中的每一个不等式,再求解集的公共部分.【详解】由-x≤1,得x≥-1,则不等式组的解集为-1≤x<3.故选:B.【点睛】此题考查在数轴上表示不等式的解集.解题关键是求不等式组的解集,判断数轴的表示方法,注意数轴的空心、实心的区别.9.已知三个实数a,b,c满足a﹣2b+c<0,a+2b+c=0,则()A.b>0,b2﹣ac≤0B.b<0,b2﹣ac≤0C.b>0,b2﹣ac≥0D.b<0,b2﹣ac≥0【答案】C【解析】【分析】根据a﹣2b+c<0,a+2b+c=0,可以得到b与a、c的关系,从而可以判断b的正负和b2﹣ac的正负情况.【详解】∵a﹣2b+c<0,a+2b+c=0,∴a+c=﹣2b,∴a﹣2b+c=(a+c)﹣2b=﹣4b<0,∴b>0,∴b2﹣ac=222222a c a ac cac+++⎛⎫-=⎪⎝⎭=222242a ac c a c-+-⎛⎫= ⎪⎝⎭…,即b>0,b2﹣ac≥0,故选:C.【点睛】此题考查不等式的性质以及因式分解的应用,解题的关键是明确题意,判断出b 和b 2-ac 的正负情况.10.如图,用长为40米的铁丝一边靠墙围成两个长方形,墙的长度为30米,要使靠墙的一边不小于25米,那么与墙垂直的一边的长度x 的取值范围为( )A .0米5x <≤米B .103x ≥米C .0米103x <≤米 D .103米5x ≤≤米 【答案】D【解析】【分析】 设与墙垂直的一边的长为x 米,根据铁丝长40米,墙的长度30米,靠墙的一边不小于25米,列出不等式组,求出x 的取值范围即可.【详解】解:设与墙垂直的一边的长为x 米,根据题意得:4032540330x x -≥⎧⎨-≤⎩, 解得:103≤x≤5; 故选:D .【点睛】此题考查了一元一次不等式组的应用,解题的关键是读懂题意,找出之间的数量关系,列出不等式组,注意本题要用数形结合思想.11.若关于x 的不等式组324x a x a <+⎧⎨>-⎩无解,则a 的取值范围是( ) A .a≤﹣3B .a <﹣3C .a >3D .a≥3 【答案】A【解析】【分析】利用不等式组取解集的方法,根据不等式组无解求出a 的取值范围即可.【详解】∵不等式组324x a x a <+⎧⎨>-⎩无解, ∴a ﹣4≥3a+2,解得:a≤﹣3,故选A .【点睛】本题考查了一元一次不等式组的解集,熟知一元一次不等式组的解集的确定方法“同大取大、同小取小、大小小大中间找、大大小小无处找”是解题的关键.12.已知关于x 的不等式组3211230x x x a --⎧≤-⎪⎨⎪-<⎩恰有3个整数解,则a 的取值范围为( ) A .12a <≤B .12a <<C .12a ≤<D .12a ≤≤【答案】A【解析】【分析】先根据一元一次不等式组解出x 的取值范围,再根据不等式组只有三个整数解,求出实数a 的取值范围即可.【详解】 3211230x x x a --⎧≤-⎪⎨⎪-<⎩①②, 解不等式①得:x≥-1,解不等式②得:x<a , ∵不等式组3211230x x x a --⎧≤-⎪⎨⎪-<⎩有解, ∴-1≤x<a ,∵不等式组只有三个整数解,∴不等式的整数解为:-1、0、1,∴1<a≤2,故选:A【点睛】本题考查一元一次不等式组的整数解,解答此题要先求出不等式组的解集,求不等式组的解集要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.13.若关于x 的不等式组21x x a <⎧⎨>-⎩无解,则a 的取值范围是( ) A .3a ≤-B .3a <-C .3a >D .3a ≥ 【答案】D【解析】【分析】利用不等式组取解集的方法:大大小小找不到即可得到a 的范围.【详解】∵关于x的不等式组21xx a<⎧⎨>-⎩无解,∴a-1≥2,∴a≥3.故选:D.【点睛】考查了一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.14.关于x的不等式组x15x322x2x a3><+⎧-⎪⎪⎨+⎪+⎪⎩只有4个整数解,则a的取值范围是()A.145a3-≤≤-B.145a3-≤<-C.145a3-<≤-D.145a3-<<-【答案】C【解析】【分析】首先确定不等式组的解集,先利用含a的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a的不等式,从而求出a的范围.【详解】解:不等式组的解集是2-3a<x<21,因为不等式组只有4个整数解,则这4个解是20,19,18,17.所以可以得到16≤2-3a<17,解得-5<a≤-143.故选:C.【点睛】此题考查解不等式组,正确解出不等式组的解集,正确确定2-3a的范围,是解决本题的关键.15.不等式组32110xx-<⎧⎨+≥⎩的解集在数轴上表示正确的是()A.B.C.D .【答案】D【解析】【分析】 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】32110 x x -<⎧⎨+≥⎩①② 解不等式①得,1x <,解不等式②得,1x ≥-所以,不等式组的解集为:-11x ≤<,在数轴上表示为:故选D.【点睛】先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.16.不等式组53643x x x +>⎧⎨+>-⎩的整数解的个数是( ) A .2B .3C .4D .5【答案】C【解析】【分析】先分别求出每一个不等式的解集,然后确定出不等式组的解集,最后确定整数解的个数即可.【详解】 53643x x x +>⎧⎨+>-⎩①②, 由①得:x>-2,由②得:x<3,所以不等式组的解集为:-2<x<3,整数解为-1,0,1,2,共4个,故选C.【点睛】本题考查了一元一次不等式组的整数解,熟练掌握解一元一次不等式组的方法以及解集的确定方法是解题的关键.解集的确定方法:同大取大,同小取小,大小小大中间找,大大小小无解了.17.在数轴上表示不等式x<2的解集,正确的是()A .B .C .D .【答案】A【解析】【分析】把不等式x<2的解集在数轴上表示出来可知答案.【详解】在数轴上表示不等式x<2的解集故选:A.【点睛】本题运用了不等式的解集在数轴上的表示方法,体现了数形结合的数学思想.18.不等式组3433122xx x-≥⎧⎪⎨-<+⎪⎩的解集在数轴上表示正确的是()A.B.C.D.【答案】A【解析】【分析】解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解).【详解】3433122x x x -≥⎧⎪⎨-<+⎪⎩①② 解①,得1x ≤-解②,得5x >-所以不等式组的解集是51x -<≤-在数轴表示为故选:A 【点睛】不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.19.如图,不等式组315215x x --⎧⎨-<⎩„的解集在数轴上表示为( ) A .B .C .D . 【答案】C 【解析】【分析】根据解一元一次不等式组的步骤:先解第一个不等式,再解第二个不等式,然后在数轴上表示出两个解集找公共部分即可.【详解】由题意可知:不等式组315215x x ①②--⎧⎨-<⎩„,不等式①的解集为2x ≥-,不等式②的解集为3x <,不等式组的解集为23x -≤<,在数轴上表示应为. 故选C .【点睛】本题主要考查了一元一次不等式组的解法,熟知和掌握不等式组解法的步骤和在数轴上表示解集是解题关键.20.解不等式组3422133xx x-≥⎧⎪⎨+>-⎪⎩①②时,不等式①②的解集在同一条数轴上表示正确的是( )A.B.C.D.【答案】D【解析】【分析】先求出不等式组中各个不等式的解集,再利用数轴确定不等式组的解集.【详解】解不等式①得:1x≤-,解不等式②得:5x<,将两不等式解集表示在数轴上如下:故选:D.【点睛】本题考查了解一元一次不等式组,在数轴上表示不等式的解集解不等式组时要注意解集的确定原则:同大取大,同小取小,大小小大取中间,大大小小无解了.。
不等式的基础练习题1.解不等式322(1)x x +>-,并将解集在数轴上表示出来.2.解不等式组12(1)01132x x x --<⎧⎪⎨-+<⎪⎩ ① ②3.解不等式组3(21)42132 1.2x x x x ⎧--⎪⎪⎨+⎪>-⎪⎩≤,把解集表示在数轴上,并求出不等式组的整数解.4.不等式组10x x -<⎧⎨>⎩的解是____________. 5解不等式组331213(1)8x x x x -⎧++⎪⎨⎪--<-⎩,,≥并写出该不等式组的整数解.6.把一个不等式组的解集表示在数轴上,如图所示,则该不等式组的解集为( )A.102x <≤ B.12x ≤ C.102x <≤ D.0x > 7.不等式组2752312x xx x -<-⎧⎪⎨++>⎪⎩的整数解是 .8. 不等式2x -7<5-2x 的正整数解有( )A .1个B .2个C .3个D .4个9.不等式组⎩⎨⎧+++-145123x x x x 的解集是 54321-----0 1 2 3 02第5A 、x<34B 、x<23C 、34<x<23D 、无解 10.小颖准备用21元钱买笔和笔记本.已知每支笔3元,每个笔记本2元,她买了4个笔记本,则她最多还可以买( )支笔.A .1B .2C .3D .411.解集在数轴上表示为如图1所示的不等式组是( ) A .32x x >-⎧⎨⎩≥ B .32x x <-⎧⎨⎩≤ C .32x x <-⎧⎨⎩≥ D .32x x >-⎧⎨⎩≤ 12.已知不等式x +8>4x +m (m 是常数)的解集是x <3,求m 13.解不等式组⎪⎩⎪⎨⎧>+<.032,231x x14.不等式215x ->的解集是 .15.不等式20x ->的解集是 .16.解不等式组⎩⎨⎧--≥+06x 21x 5x 3>,并把它的解集在所给的数轴上表示出来。
解方程不等式组练习题一、求解以下方程组:1.$$\begin{cases}2x+3y=11 \\3x-2y=7\end{cases}$$解:首先,我们可以利用消元法将方程组变为:$$\begin{cases}4x+6y=22 \\9x-6y=21\end{cases}$$将第二个方程两边乘以3,得到$9x-6y=21$,与第一个方程相加,消去$y$的项:$$\begin{cases}4x+9x=22+21 \\13x=43\end{cases}$$化简得到:$x=\frac{43}{13}$,代入第一个方程中求得$y=\frac{5}{13}$。
所以,方程组的解为$x=\frac{43}{13}$,$y=\frac{5}{13}$。
2.$$\begin{cases}3x+5y=19 \\2x-4y=10\end{cases}$$解:我们可以利用消元法将方程组变为:$$12x+20y=76 \\10x-20y=50\end{cases}$$将第二个方程两边乘以$2$,得到$10x-20y=50$,与第一个方程相加,消去$y$的项:$$\begin{cases}12x+10x=76+50 \\22x=126\end{cases}$$化简得到:$x=\frac{126}{22}$,代入第一个方程中求得$y=\frac{1}{22}$。
所以,方程组的解为$x=\frac{63}{11}$,$y=\frac{1}{22}$。
二、求解以下不等式组:1.$$x+2y\geq 3 \\2x+y\leq 5\end{cases}$$解:首先,我们可以将第一个不等式化简为$y\geq \frac{3-x}{2}$,将第二个不等式化简为$y\leq 5-2x$。
绘制两个不等式的图像,并找出它们的交集部分:[图像略]从图中可以看出,交集部分为不等式组的解集。
所以,不等式组的解为$y\geq \frac{3-x}{2}$,$y\leq 5-2x$。
不等式解方程练习题1. 解不等式:√(3x-7)≤ 2首先,我们需要将不等式转化为一个方程。
不等式中的根号(√)表示的是非负数,所以我们可以先将不等式两边都平方,得到:3x-7 ≤ 4接下来,我们解这个方程:3x ≤ 11x ≤ 11/3所以,不等式的解集是x ≤ 11/3。
2. 解不等式:2x+5 > 3x-1我们将不等式转化为方程,得到:2x + 5 = 3x - 1将 x 的项移到一边,常数项移到另一边:5 + 1 = 3x - 2x6 = x所以,这个方程的解是 x = 6。
为了验证这个解是否满足原始的不等式,我们可以将 x = 6 代入原始不等式:2(6) + 5 > 3(6) - 112 + 5 > 18 - 117 > 17由于 17 不大于 17,所以 x = 6 不满足原始的不等式。
因此,这个不等式没有解。
3. 解不等式:4x-3 ≤ 2x+9我们将不等式转化为方程,得到:4x - 3 = 2x + 9将 x 的项移到一边,常数项移到另一边:4x - 2x = 9 + 32x = 12x = 6所以,这个方程的解是 x = 6。
为了验证这个解是否满足原始的不等式,我们可以将 x = 6 代入原始不等式:4(6) - 3 ≤ 2(6) + 924 - 3 ≤ 12 + 921 ≤ 21由于 21 小于或等于 21,所以 x = 6 满足原始的不等式。
因此,这个不等式的解集是 x = 6。
4. 解不等式:(x+1)(x-2) > 0我们可以使用数轴图来解这个不等式。
首先,我们找到不等式左边的等式 (x+1)(x-2) = 0 的解。
当 (x+1)(x-2) = 0 时,要么 x+1 = 0,要么 x-2 = 0。
解得 x = -1 或 x = 2。
现在,我们将数轴分成三个区间:(-无穷,-1),(-1,2),(2,+无穷)。
在每个区间,我们选择一个测试点来确定不等式的符号。