工程流体力学-绘制静水压强分布图

则有
P dP sinyc A
hc A pc A
2、总压力作用点（压心）
设总压力P的作用点为D点 合力矩定理：
P yD y dP sin y2dA
A
受压面A对ox轴的惯性矩 A y 2dA Io Ic yc2 A
则有
yD
sin Io
P
Io yc A
yc
Ic yc A
第六节 液体作用在平面上的总压力
一、静水压强图示（压强分布图） 静水压强分布图绘制原则：
1、根据基本方程式 p=h 绘制静水压强大小；
2、静水压强垂直于作用面且为压应力； 3、在受压面承压的一侧，以一定比例尺的矢量
线段表示压强的大小和方向。
h1பைடு நூலகம்
h1
h
h2
h1
h1 h1 h2
h2
h
h2
❖受压面为平面的情况下，压强分布图的外包线为 直线；当受压面为曲面时，曲面的长度与水深不成 直线函数关系，故压强分布图外包线亦为曲线。
（一）为何要重视老年人用药？
2 老年人用药机会多 上海市药品不良反应监测中心正在进行的一项“上海
市 中老年人群药物流行病学研究”显示，上海市54％的
中 老年人（50岁以上）患有各种慢性疾病，每个月有58 ％的中老年人会看病，每年有91％的中老年人会服用 药物，每个月会有78％的中老年人会服用药物。
二、 药物商品选择的原则即合理用药的基本要素
安全性 （首要条件）
有效性
要素
经济性
适当性
第一节 药物商品的选择和使用
给药的适当性
治疗目标 疗程
药物 剂型
病人 途径
剂量 时间
第一节 药物商品的选择和使用

- 1 -
版权所有，仿冒及翻印必究
水力分析与计算
水力分析与计算
静水压强分布图及其绘制
1.静水压强分布图
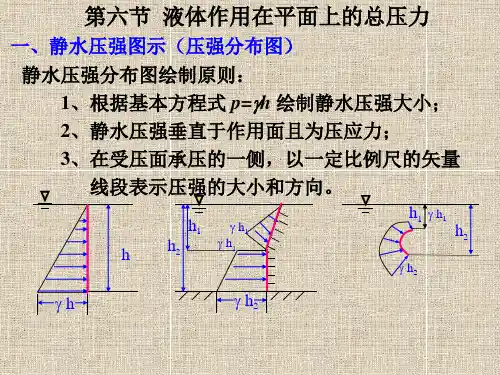
根据静水压强的基本公式h p γ=知道，压强p 的大小与水深h 成线性函数关系，因此可以将作用面上的压强沿水深的分布绘制成几何图形，即静水压强分布图。

2.静水压强分布图的绘制方法如下：
(1)用静水压强的基本公式计算出静水压强的数值，
用一定的比例尺箭杆长度代表该点静水压强的大小。

(2)用箭头表示静水压强的方向(垂直作用面)。

(3)连接箭杆的尾部构成的几何图形，就构成受压面
上的静水压强分布图。

对于平面壁，压强p 沿水深h 方
向呈直线分布，只要确定两个点的压强值，就可以确定
该直线。

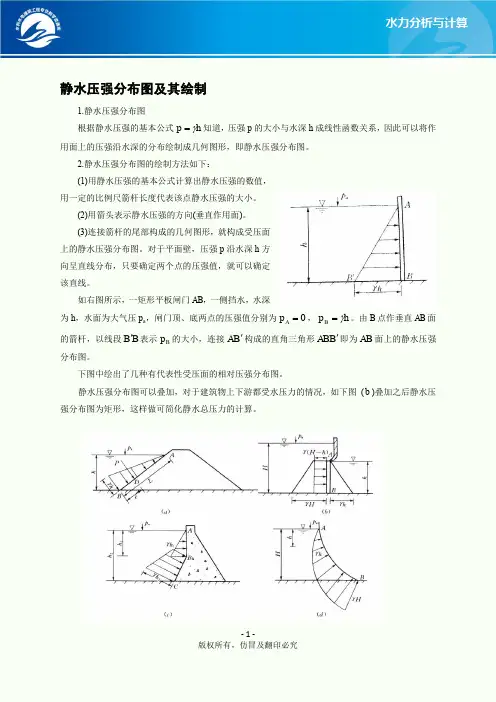
如右图所示，一矩形平板闸门AB ，一侧挡水，水深
为h ，水面为大气压p a ，闸门顶、底两点的压强值分别为0=A p ，h p B γ=。

由B 点作垂直AB 面的箭杆，以线段B B '表示B p 的大小，连接B A '构成的直角三角形B AB '即为AB 面上的静水压强分布图。

下图中绘出了几种有代表性受压面的相对压强分布图。

静水压强分布图可以叠加，对于建筑物上下游都受水压力的情况，如下图 (b )叠加之后静水压强分布图为矩形，这样做可简化静水总压力的计算。

Байду номын сангаас
C
D
C
C
5
2
总压力作用点
hc P F
h dP
α E
O
O O
D
C
dA
对Ob轴取矩得
2 A A
L
2
PLD Lp dA g L sin dA g sin L d A
A
令 I L A
2 b A
L’
6
表示平面EF对Ob轴的面积惯性矩。
由平行移轴定律得 化简
I b I c Lc A
方向: 垂直指向受压面
2
P 作用点：过 压强分布图 形心,且位于 对称轴上.
A
B
P C
3
(2)
O
解
析 法:
hc
P
F
h dP
α E
O
C D L
dA
P g sin Lc A g hc A pc A
4
大小: P=pcA, pc—形心处压强
方向: 垂直指向受压平面 作用点:
I y =y + y A
2
Ic LD Lc Lc A
（1-50）
可见，LD > LC 即，总压力的作用点在形心之下 （平面水平放置时重合）
上式控制总压力作用点深度位置。
7
bD 的确定：将静水压力对OL轴取矩，则
Pb D bp d A bL sin d A sin Lb d A
1-9
一
作用于平面上的静水总压力
压力图法(图解法), 解析法
两种方法:
静水压强分布图的绘制
•用一定比例的线段长度代表静水压强的大小; •用与作用面垂直的箭头表示静水压强方向。

工程流体力学实验实验一 静水压强实验一、实验目的1、通过实验加深对流体静力学基本方程h p p γ+=0的理解。

2、验证静止流体中不同点对于同一基准面的测压管水头为常数，即=+γpz 常数3、实测静水压强，掌握静水压强的测量方法。

4、巩固绝对压强、相对压强、真空度的概念，加深理解位置水头、压力水头以及测压管水头之间的关系。

5、已知一种液体重度测定另一种液体的重度。

二、实验原理γ3图1 静水压强实验原理图静水压强实验原理如图1所示，相对静止的液体只受重力的作用，处于平衡状态。

以p 表示液体静压强，γ表示液体重度，以z 表示压强测算点位置高度（即位置水头），流体静力学方程为=+γp z 常数上式说明 1、在重力场中静止液体的压强p 与深度h 成线性分布，即4030403h h h h p p p p --=--2、同一水平面（水深相同）上的压强相等，即为等压面。

因此，水箱液面和测点3、4处的压强（绝对压强）分别为00h p p a γ+=()03∆-∆+=γa p()04∆-∆+=γa p33h p p a γ+=()33z p a -∆+=γ44h p p a γ+=()44z p a -∆+=γ与以上各式相对应的相对压力（相对压强）分别为a p p p -='000h γ= ()03∆-∆=γ()04∆-∆=γa p p p -='333h γ= ()33z -∆=γa p p p -='444h γ= ()44z -∆=γ式中 a p —— 大气压力，Pa γ—— 液体的重度，3m N0h —— 液面压力水头，m0∆ —— 液面位置水头，m3∆、4∆—— 3、4处测压管水头，m3z 、 4z —— 3、4处位置水头，m3h 、4h —— 3、4处压力水头，m3、静水中各点测压管水头均相等，即43∆=∆或 γγ'+='+4433p z p z 或 4433h z h z +=+即测压管3、4的液位在同一平面上。

u x u（ x x，y，z，t） u y u（ y x，y，z，t） u u（x，y，z，t） z z
p p（x，y，z，t）
（x，y，z，t）
因欧拉法较简便，是常用的方法。
三、欧拉加速度 质点的加速度（流速对时间求导）有两部分组成： 1、当地加速度（local acceleration） ——流动过程中流体由于速度随时间变化而引 起的加速度； 2、迁移加速度（ connective acceleration ）——流动过程中流体由于速度随位置变 化而引起的加速度。 由于位置又是时间t的函数，所以流速是t的复合函数，对流速求导可得加速度：
IC y D yC ，yC 在变 yC A
例1
一水池侧壁AB，已知水深h，宽为b，求作用在侧壁AB上的总压力及作用点。
o
A yD =2h/3
C
h
Fp ρgh B
D
b
h
yC
二、图算法
1 Fp gh 2 b Ap b 2
o yD =2h/3 yC Ap C
h
Fp ρgh
D
b
原理：静水总压力大小等于压强分布图的体积，其作用线通过压强分布图的 形心，该作用线与受压面的交点便是压心D。
h
o
Ap h Fp ρgh ρgh
Fp
D
Ap
h
2h/3
1 Fp Ap b gh2 b 2 2 yD h 3
例2
一铅直矩形闸门AB，已知h1=1m，h2=2m，宽b=1.5m，求总压力及其作用点。
u 判别式： 0 t p 0 t u x u y t t
u u（x，y，z）
p p（x，y，z）

④ 利用水压曲线，推算其它各点的压力值。
3 水压图的组成
纵横坐标系 管道的平面展开图 地形剖面、各热用户系统的充水高度和 汽化水头线 静水压线和供回水管动水压曲线
二 水压图的绘制
水压图是热水网路设计和运行的重要 依据。
1 水压图的绘制的基本技术要求
① 不超压 ② 与热水网路直接连接的用户系统，网路的
2
2
p 1g1 Z2 1 p 2g2Z 2 2 p 1 2
用水头高度的形式表示 ：
pg 1Z121 g 2 pg 2Z22g 2 2H 12 mH2O
测压管水头
将管路各节点的测压管水头高度顺次连接起 来的曲线，称为热水管路的水压曲线。
P12 ——水流经管段l—2的压力损失，Pa； H12 ——水流经管段l—2的压头损失， mH2O。
本讲主要内容
水压图的基本概念 水压图的绘制
一 水压图的基本概念
水力计算只能确定热水管道中各管段的 压力损失（压差）值，不能确定热水管道上 各点的压力（压差）值。而绘制的水压图， 可以清楚地表示出热水管路中各点的压力。
1 绘制水压图的基本原理
流体力学中的伯努利能量方程式是绘制水 压图的理论基础。
设热水流过某一管段，根据伯努利能量方 程式，可列出断面1和2之间的能量方程式为：
系统的充水高度 。
2. 网路回水管内任何一点的压力，都应比 大气压力至少高出5mH2O，以免吸入空气。
④ 压力满足
1.
供、回水管的资用压差，应满足热力站
或用户所需的作用压力。
2 水压图的绘制的步骤和方法
① 定坐标，定基准面 以网路循环水泵的中心线的高度（或其
它方便的高度）为基准面。
②定静水压线位置
压力不应超过该用户系统用热设备及其管道 构件的承压能力。

ρg
18
说明静水压强对该液体质点作的功为 dm g 的这种做功本领称为液体的压强势能。
p1 。液体压强 ρg
所以， 1 ρg 就是单位重量液体在1点相对于大气压的压强 p 势能，即单位压能。 由于位能和压能均为势能，所以又将液体的单位位能z与单位
压能 p1 ρg 之和称为单位重量液体的势能，简称单位势能。 能量意义：在质量力仅为重力作用的同种相互连通的平衡液体中， 任意点相对同一位置和压强基准的单位势能都相等。 它反映了重力作用下平衡液体中能量的守恒与转换的规律， 位能和压能二者等值相互转换，总和不变。
11
2 液柱单位
根据的关系可知，任何一种压强（包括绝对压强、相对压
强和真空压强）的大小，都可以等效地用某种已知容重液体的
液柱高度来表示。
工程中，常用的液柱高度为水柱高度和汞柱高度，其单位
为mH2O、mmH2O和mmHg。 1mH2O产生的压强为9.8kPa和1000kgf/m2；
1mmH2O产生的压强为9.8Pa和1kgf/m2;
（2）用箭头在线段的一端标出静水压强的方向,并垂直指向受
压面; （3）在线段的另一端画出压强分布的外包络线。
1
2
第四节 液柱式测压计
液柱式测压计是以水静力学基本方程原理为基础，将被测压 强转换成液柱的高差进行测量的测压计。其简单、直观、精度较 高，但测量范围较小，故常用在实验室或实际生产中测量低压、
p f(x.y.z)
9
讨论： （1）设液面的 z 轴坐标用zs表示，则将 p=p0 代入上(A)式可 得液面方程为
ω2 2 ω2r 2 zs x y2 2g 2g 上式表明，液面为一旋转抛物面。因为液体中任一点的水深，则

作用点：过FPx和FPz的交点，作与水平方 向成α角的线延长交曲面于D点
第14页/共28页
前进
y
oM
N
x
z
h dFp E dFp dFpz
F
K
L
dFpx
K
(dA)x
L
❖曲面上静水总压力的水平分力等于(dA) z
曲面在铅垂投影面上的静水总压力。
Fpx ghc Ax Pc Ax
❖曲面上静水总压力的垂直压力等于 压力体内的水体重。 FPz gV
静水总压力与水平方向的夹角：
arctan
FPz FPx
29.68
静水总压力的作用点：ZD R sin 2 sin 29.68 1m
答：略。
返回
第26页/共28页
结束
第27页/共28页
谢谢您的观看！
第28页/共28页
F三角
分布图叠加，直接求总压力
h1
e F矩形
h2
FP
b
(h2
h1) ( gh1
2
gh2 )
b
117.6kN
方向向右
依力矩定理：
Fp
e
F三角
[h2
h1
3
h2
]
F矩形
h2 2
可解得：e=1.56m
答：略
返回
第24页/共28页
一垂直放置的圆形平板闸门如
O
图所示，已知闸门半径R=1m，形心 在水下的淹没深度hc=8m，试用解析
注意：
1.平衡液体的自由表面是等压面。 2.不同流体的交界面是等压面。 3.讨论等压面必须保证是同一种连续介质
连通容器
连通容器
第6页/共28页

hM

pM
g
41.56 9.8
4.24m水柱
用绝对压强表示： pMabs pM pa 41.56 98 56.44kN / m2
pM

56.44 98
0.576个大气压
hM

pMabs
g
56.44 9.8
5.76m水柱
用真空度表示：真空值 pv 41.56kN / m2 0.424 个大气压
式（2-1）（2-2）以不同的形式表示重力作用下液体静压强的分 布规律，均称为液体静力学基本方程式。
• 2、推论
由液体静力学基本方程
p p0 g(H z) p0 gh (2-1)
或 当 p0 0 时， p gh
结论：1）仅在重力作用下，静止流体中某一点的静压强随深度按
线性规律增加。
2）自由表面下深度h相等的各点压强均相等——只有重力作用下
的同一连续连通的静止流体的等压面是水平面。
3）推广：已知某点的压强和两点间的深度差，即可求另外一点的
压强值。
p2 p1 gh （2-3）
4)平衡状态下，液体内（包括边界上）的任意点压强的变化，等
值地传递到其他个点（帕斯卡原理）。
重力作用下流体静压强的分布规律，如图右所示。
由重力作用下的静力学基本方程
Z p C
g
或:
Z1

p1
g

Z2

p2
g
1.各项物理意义
a.位置水头z ：任一点在基准面0-0以上的位置高度，表示单位重量
流体从某一基准面算起所具有的位置势能，简称位能。
b.测压管高度p/ρg：表示单位重量流体从压强为大气压算起所具有

1 FX p X dA X p n dAn cos( n, X ) Xdxdydz 0 6
因为
1 dAn cos( n, X ) dAx dydz 2
代入上式得：
3 当四面体无限地缩小到0点时，上述方程中最后一项近于 零，取极限得, 即 p p
X n
p X pn
②质量力：（只有重力、静止）如图所示
1 其质量为 dxdydz ，单位质量力在各方向上的分别为 6
X、Y、Z，则质量力在各方向上的分量为
1 1 1 Xdxdydz , Ydxdydz , Zdxdydz 6 6 6
FX 0, FY 0, FZ 0
•以X方向为例：
学习重点
1、静水压强的两个特性及有关基本概念。 2、重力作用下静水压强基本公式和物理意 义。 3、静水压强的表示和计算。 4、静水压强分布图和平面上的流体总压力 的计算。 5、压力体的构成和绘制以及曲面上静水总 压力的计算。 6、处于相对平衡状态的液体中压强的计算。
§2-1
若在静止液体中任取两点l和2，点1和点2压强各为p1和p2， 位置坐标各为z1和z2，则可把式
p z c g
改写成另一表达式，即： z1
p1
p1 p2 z2 g g
1
z1
p2
2
z2
0 0 静压强基本方程的几何意义和物理意义
为了进一步理解静水压强基本方程式，现在来讨 论该方程的物理意义和几何意义 1.物理意义 式中：
pA g
A
Z
x y
如图所示，在一密闭容器中盛有密度为ρ 的液体，若自由液面上的 压强为p0、位置坐标为z0，则在液体中位置坐标为z的任意一点A的压强 p可由该式得到，即

sinJ x
si yC
说明各项意义，一般情况下D在C下方。
实际工程中的受压面多是轴对称面，总压力P的作用点 必位于对称轴上，这就完全确定了D的位置。
15
§2-8 作用在曲面上的静水总压力
一、原则 Px dpx
PZ dpZ
P Px2 Pz2
二、静水总压力的水平分力
p1d p2d (z1 z2 )d 0
整理
z1
p1
z2
p2
即 z+ p = c
（2-2-2）
4
或
p1d p2d hd 0
整理
p2 p1 h
（2-2-1）
当p柱=p体0 +上h底面与液面齐平时，若液面压强为p0，则（2-2-3）
式（2-2-2）和（2-2-3）为重力作用下水静力学基本方程的两 种表现形式，
❖
P =P -pa
abs
如图：若 p0 为相对压强，
P P rh P P rh P
B
0
Babs
0
a
7
若P0 为绝对压强，
p Babs
p 0
h
若开口（不封闭） p h B
p p h p
B
0
a
p p h
Babs
a
以后无特殊说明，指相对压强。
3、真空及真空度：当液体中某一点
的绝对压强小于当地大气压强时，
12
右图示： P1 h1lb
e1
2
P2
1
2
(h2
h1 )b
e2 3
P
P1
P2
1 2
(h1
h2
)b
Px P1e1 P2e2

P12 ——水流经管段l—2的压力损失，Pa； H12 ——水流经管段l—2的压头损失， mH2O。
2 利用水压图分析系统中管路的水力工况
① 利用水压曲线，可以确定管道中任何一点的 压力（压头）值。 管道中任意点的压头就等于该点测压管水 头高度和该点所处的位置高度之间的高差， 也就是该点的测压管水柱高度。
2
2
p 1g1 Z2 1 p 2g2Z 2 2 p 1 2
用水头高度的形式表示 ：
pg 1Z121 g 2 pg 2Z22g 2 2H 12 mH2O
测压管水头
将管路各节点的测压管水头高度顺次连接 起来的曲线，称为热水管路的水压曲线。
•
9、别再去抱怨身边人善变，多懂一些道理，明白一些事理，毕竟每个人都是越活越现实。
•
10、山有封顶，还有彼岸，慢慢长途，终有回转，余味苦涩，终有回甘。
•
11、人生就像是一个马尔可夫链，你的未来取决于你当下正在做的事，而无关于过去做完的事。
•
12、女人，要么有美貌，要么有智慧，如果两者你都不占绝对优势，那你就选择善良。
•
16、成功的秘诀在于永不改变既定的目标。若不给自己设限，则人生中就没有限制你发挥的藩篱。幸福不会遗漏任何人，迟早有一天它会找到你。
•
17、一个人只要强烈地坚持不懈地追求，他就能达到目的。你在希望中享受到的乐趣，比将来实际享受的乐趣要大得多。
•
18、无论是对事还是对人，我们只需要做好自己的本分，不与过多人建立亲密的关系，也不要因为关系亲密便掏心掏肺，切莫交浅言深，应适可而止。
纵横坐标系 管道的平面展开图 地形剖面、各热用户系统的充水高度和 汽化水头线 静水压线和供回水管动水压曲线
二 水压图的绘制

Pz 的方向： 当液体和曲面的位于同侧时，Pz 向下 当液体和曲面不在同一侧时，Pz 向上
有
液
体
A
a
无
液
A
体
• 3.静水总压力
P Px2 Pz 2
• 总压力的作用点为水平线交角
arctan Pz
Px
例题4: 如图所示为一溢流坝上的弧形门。已 知：R=10m，门宽b=8m，α=30ο，试求：作用 在弧形闸门上的静水总压力及压力中心的位置
p1
z2
p2
或
• 在重力作用下连通的
同种静止液体中： ① 压强随位置高程线性 变化； ② 等压面是水平面，与 质量力垂直；
③ z p 是常数。
z pC
3. 绝对压强、相对压强、真空
• 压强 p基准点不同，可将压强分为：
（1）绝对压强 以完全真空为零点，记 为 p其值总为正值
（2）相对压强 以当地大气压为
(4
1.34
30 360
102
1 2
5
8.66)
9.8 8
774.6KN
静水总压力
P Px2 Py2 25482 774.12 2663KN
合力与水平线的夹角
tg 1( pz ) tg 1( 774.6) 16.91
px
2548
压力中心D h D 4 10 sin16.91 6.91m
五. 压强的量测
• 用测压管测量
测压管的一端接大气，这样就把测管水头揭示出 来了。再利用液体的平衡规律，可知连通的静止液体 区域中任何一点的压强，包括测点处的压强。
A
α
pA h l sin
如果连通的静止液体区域包括多种液体，则须在 它们的分界面处作过渡。

（3）因铰点在A处，则作用于闸门的所有外力对此点之力矩总和必为0，即
P( yD −
F=
1.5 . . o ) − G×1 0 − F × 2 0 = 0 sin45
得阻止闸门的开启力
153860 3.54+0.14−2.12)−3000×1 ( 2
= 118511 N
第七节 液体作用在曲面上的总压力
空气
= 0.9 + 0.9×1.8×1.2 = 1.2m
1.2× .83 1 12
对左侧水箱 （a） 将空气生产的负压换算成以m水柱表示的负压h值相当于水箱液面下降 1.5m，而成为虚线面，可直接用静水力学基本方程求解，这样比较方便。 因为 −0.147×105 h = 9800 = −1.5m 所以有：F2= γ hc2 A = 9800×（2.2+0. 9）×1. 8×1.2=65621N（方向向右）
例2 有一铅直半圆壁（如图）直径位于液面上，求F值大小及其作用点。 有一铅直半圆壁（如图）直径位于液面上， 值大小及其作用点。 解：由式 F = γ sin θyc ⋅ A = γhc A = pc A 得总压力
F = pc A = γhc A 4d 1 2 1 3 =γ ⋅ ⋅ πd = γ ⋅ d 6π 8 12
例3 如图所示，左边为水箱，其上压力表的读数为-0.147×105Pa，右边为油 如图所示，左边为水箱，其上压力表的读数为-0.147× Pa， 油的γ 用宽为1.2 m的闸门隔开 闸门在A点铰接。 的闸门隔开， 箱，油的γ′=7350N/m3，用宽为1.2 m的闸门隔开，闸门在A点铰接。为使闸 AB处于平衡 必须在B点施加多大的水平力F 处于平衡， 门AB处于平衡，必须在B点施加多大的水平力F’。 解 确定液体作用在闸门上的力的大小和作用点位置。 对右侧油箱 F1= γ hc1 A = 7350×0. 9×1. 8×1.2=14288N Ic1 yD1 = yc1 + y A （方向向左） c1 o 水 5.5 m F2 B 压力表 1.5 m o A F1 油 1.8 m F 2.2 m

如图可测水中大于大气压的相对压强
pa p0

A
p gh;
h
测压管
2、 U 形管测压计 当被测流体压强较大时，常采用图所示的U形管测压计在 h2 。则有 连续静止的汞中读出h1 、
p1 p gh 1
p2 pa m gh2
由于U形管1、2两点在同一等压面上， p1 得A点的相对压强
教学基本要求
1、正确理解静水压强的两个重要的特性和等压面的性质。 2、掌握静水压强基本公式和物理意义，会用基本公式进行 静水压强计算。 3、掌握静水压强的单位和三种表示方法：绝对压强、相对 压强和真空度；理解位置水头、压强水头和测管水头的物理 意义和几何意义。 4、掌握静水压强的测量方法和计算。 5、会画静水压强分布图，并熟练应用图解法和解析法计算 作用在平面上的静水总压力。 6、会正确绘制压力体剖面图，掌握曲面上静水总压力的计 算。 7 、会计算液体的相对平衡
势能。位势能和压强势能之和称为单位重量流体的总势能。 所以静水压强基本方程表示在重力作用下静止流体中各点的 单位重量流体的总势能是相等的。这就是静止液体中的能量 守恒定律。
2.几何意义
单位重量流体所具有的能量也可以用液柱高度 来表示，并称为水头。 式中：
z 具有长度单位，如图所示，z 是流体质点离基准面
p p0 gh 98 1 9.81 107.8kN / m 解：
2
p0=pa
h
p p pa 107.8 98 9.8kN / m2
例2：如图已知， p0=50kN/m2，h=1m， 求：该点的绝对压强及相对压强 解：p p0 gh 50 1 9.8 1 59.8kN / m2

pm pab pa gh p
pv
c.真空度pv
pv pa pab
注意：pv表示绝对压强小于当地大气压强而形成 真空的程度，读正值！
.精品课件.
15
3.压强单位 标准大气压（atm） =1.013×105Pa=760mmHg=10.33mH2O 工程大气压（at） =0.9807×105Pa=735.5mmHg=10mH2O =1kg/cm2（每平方厘米千克力，简读公斤）
x y z 对（1）、（2）、（3）式坐标交错求偏导，整理得
X Y y x
Y Z z y
Z X x z
——力作功与路径无关的充分必要条件 必存在势函数U，力是有势力
dU
U x
dx
U y
dy
U dz .精品课z 件.
8
U X x
U Y y
U Z z
——力与势函数的关系
（4）式可写为：
换算： 1kPa=103Pa
1bar=105Pa
.精品课件.
16
4.测压计 一端与测点相连，一端与大气相连 例 求pA（A处是水，密度为ρ，测压 计内是密度为ρ’的水银）
解：作等压面
pA ga ' gh
pA 'h ag
例 求pA（A处是密度为ρ的空气，测压计内是密度为ρ’的 水）
解：pA ' gh
（1）用分割法求P大小，作用点为D；
或
yD
Jc yc A
h
Jc
sin
A
T
（从形心C处算起）
（2）对A点求矩
P
A
G l cos P AD Tl cos T
2
C l
D θ

流体力学Hydromechanics（浙大教程二）二、压强的表示方法及单位（如图2-12所示）图2－121.压强的表示方法a.绝对压强（absolute pressure）：是以绝对真空状态下的压强（绝对零压强）为基准计量的压强，用表示，。

b. 相对压强（relative pressure）：又称“表压强”，是以当地工程大气压(at) 为基准计量的压强。

用p表示，，p可“＋”可“–”，也可为“0”。

c.真空（Vacuum）：是指绝对压强小于一个大气压的受压状态，是负的相对压强。

真空值p v(2-13)真空高度(2-14)注意：计算时无特殊说明时均采用相对压强计算。

例1 求淡水自由表面下2m 深处的绝对压强和相对压强。

解：绝对压强：=1.194标准大气压相对压强：标准大气压例2 设如图2-13所示，h v =2m 时，求封闭容器A 中的真空值。

图2-13解：设封闭容器内的绝对压强为p abs ，真空值为P v 。

则：根据真空值定义：2.压强的计量单位a.应力单位这是从压强定义出发，以单位面积上的作用力来表示的，N/m 2，Pa ，kN/ m 2，kPa 。

b.大气压标准大气压：1标准大气压(atm)=1.013X 105Pa=101.3 kPac.液柱高水柱高mH 20：1atm 相当于1at 相当于汞柱高mmHg ：1 atm 相当于1at 相当于三、相对平衡流体静压强分布相对平衡：指各流体质点彼此之间及流体与器皿之间无相对运动的相对静止或相对平衡状态。

因为质点间无相对运动，所以流体内部或流体与边壁之间都不存在切应力。

相对平衡流体中，质量力除重力外，还受到惯性力的作用。

例1 如图2-14所示，一洒水车等加速度a =0.98m/s 2向右行驶，求水车内自由表面与水平面间的夹角；若B 点在运动前位于水面下深为h =1.0m ，距z 轴为x B =-１.5m ，求洒水车加速运动后该点的静水压强。

解：考虑惯性力与重力在内的单位质量力为（取原液面中点为坐标原点）图2-14X= -a ； Y=0 ；Z= -g代入式（2-7）得：积分得：在自由液面上，有： x=z=0 ；p=p 0得： C=p 0 =0代入上式得：Ｂ点的压强为：自由液面方程为（∵液面上p 0=0） ax+gz =0 即：例2 如图2-15所示，有一盛水的开口容器以3.6m/s2的加速度沿与水平成30o夹角的倾斜平面向上运动，试求容器中水面的倾角q ，并分析p 与水深的关系。