使用OpenGL编程实现Bresenham直线扫描转换算法

《图形学》实验四：中点Bresenham算法画直线VC++6.0，OpenGL使⽤中点Bresenham算法画直线。

1//中点Bresenham算法⽣成直线2 #include <gl/glut.h>3 #include <math.h>45#define WIDTH 500 //窗⼝宽度6#define HEIGHT 500 //窗⼝⾼度7#define DRAWLINE1 MidpointBresenham(100,200,200,100); //画直线8#define DRAWLINE2 MidpointBresenham(200,100,450,400); //画直线910#pragma comment(linker, "/subsystem:\"windows\" /entry:\"mainCRTStartup\"") //取消控制台1112void Init() //初始化13 {14 glClearColor(1.0f,1.0f,1.0f,1.0f); //设置背景颜⾊，完全不透明15 glColor3f(1.0f,0.0f,0.0f); //设置画笔颜⾊1617 glMatrixMode(GL_PROJECTION); //设置投影18 gluOrtho2D(0.0, WIDTH, 0.0, HEIGHT); //设置投影区域19 }2021void MidpointBresenham(int x0,int y0,int x1,int y1) //中点Bresenham算法画线22 {23int dx,dy,d,UpIncre,DownIncre,x,y;24if(x0>x1){25 x=x1;x1=x0;x0=x;26 y=y1;y1=y0;y0=y;27 }28 x = x0,y = y0;29 dx = x1-x0;30 dy = y1-y0;31if(dy>0&&dy<=dx){ //0<k<=132 d = dx-2*dy;33 UpIncre = 2*dx-2*dy;34 DownIncre = -2*dy;35while(x<=x1){36 glBegin(GL_POINTS);37 glVertex2i(x,y);38 glEnd();39 x++;40if(d<0){41 y++;42 d+=UpIncre;44else45 d+=DownIncre;46 }47 }48else if((dy>=(-dx))&&dy<=0) //-1<=k<=049 {50 d=dx-2*dy;51 UpIncre=-2*dy;52 DownIncre=-2*dx-2*dy;53while(x<=x1)54 {55 glBegin(GL_POINTS);56 glVertex2i(x,y);57 glEnd();58 x++;59if(d>0)60 {61 y--;62 d+=DownIncre;63 }64else d+=UpIncre;65 }66 }67else if(dy<(-dx)) //k<-168 {69 d=-dy-2*dx;70 UpIncre=2*dx+2*dy;71 DownIncre=2*dx;72while(y>=y1)73 {74 glBegin(GL_POINTS);75 glVertex2i(x,y);76 glEnd();77 y--;78if(d<0)79 {80 x++;81 d-=UpIncre;82 }83else d-=DownIncre;84 }85 }8687else//k>1和k不存在88 {89 d=dy-2*dx;90 UpIncre=2*dy-2*dx;91 DownIncre=-2*dx;92while(y<=y1)93 {94 glBegin(GL_POINTS);95 glVertex2i(x,y);96 glEnd();97 y++;98if(d<0)99 {100 x++;101 d+=UpIncre;103else d+=DownIncre;104 }105 }106 }107108void Display() //显⽰函数109 {110 glClear(GL_COLOR_BUFFER_BIT); //清空颜⾊堆栈111112 DRAWLINE1 //画直线113 DRAWLINE2 //画直线114115 glFlush(); //清空缓冲区指令116 }117118int main(int argc,char** argv)119 {120 glutInit(&argc,argv);121 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); //初始化显⽰模式122 glutInitWindowSize(WIDTH,HEIGHT); //设置窗⼝尺⼨123 glutInitWindowPosition(200,100); //设置窗⼝位置124 glutCreateWindow("画直线"); //创建窗⼝125126 glutDisplayFunc(Display); //注册显⽰函数127 Init(); //初始化128 glutMainLoop(); //进⼊程序循环129return0;130 }Freecode :。

在计算机图形学中，Bresenham算法是一种用于在离散坐标系上绘制直线段的算法。

它是一种高效的算法，能够准确地计算出直线段上的所有像素点，使得在计算机屏幕上显示出直线段来。

Bresenham算法的实现可以帮助我们更好地理解画线原理，并且在计算机视觉、图像处理等领域有着广泛的应用。

1. Bresenham算法的原理Bresenham算法是通过计算直线段的斜率来确定每个像素点的位置。

具体来说，它利用了直线的对称性和整数的特性，通过计算像素点与真实直线的距离来判断下一个像素点应该取的位置。

这样可以避免使用浮点运算，使得算法更加高效。

2. 实现Bresenham算法的关键步骤在实现Bresenham算法时，需要考虑以下几个关键步骤：- 初始化各个变量，包括起始点(x0, y0)和终点(x1, y1)，以及斜率的计算值，例如dx和dy。

- 根据斜率的正负情况，确定每个像素点的增量步长，以便在遍历过程中准确计算出像素点来。

- 利用对称性和整数特性，进行迭代计算，逐步确定直线段上的所有像素点的位置。

3. Bresenham算法的优缺点Bresenham算法作为一种离散直线段插值算法，具有以下几个优点：- 算法简单高效，节省存储空间和运算时间。

- 可以高效地解决像素化显示问题，避免了浮点运算的复杂性。

- 在硬件上实现时，只需少量的资源就能完成计算，适合嵌入式系统和图形处理器。

然而，Bresenham算法也存在一些缺点，比如对于曲线的绘制就不太奏效，因为它是基于直线段的形式来处理的。

4. 我对Bresenham算法的理解在我看来，Bresenham算法是一种经典的离散直线段插值算法，其思想简洁高效。

它通过逐步迭代的方式，计算出直线段上的所有像素点位置，使得在计算机屏幕上显示出直线段来更加精确。

这种算法的实现可以帮助我们更好地理解画线的原理，对于理解计算机图形学和计算机视觉都有着重要的意义。

总结起来，Bresenham算法作为一种高效的离散直线段插值算法，具有着重要的理论和实际价值。

实验一、直线的扫描转换系别：计算机学院专业班级： 10信科2姓名：学号实验日期： 2013-3-27 实验报告日期：2013-3-27一、实验目的：理解直线的不同生成算法，并用程序实现。

二、实验环境：1熟悉VC6.0开发平台；2熟悉OpenGL开发库；三、实验内容：1.使用OpenGL中的基本画点函数，分别使用DDA算法、中点算法、Bresenham算法画直线。

要求为每一种算法分别建立对应的函数，函数参数为直线段的端点坐标。

四、实验报告内容1、程序源码；void MidpointMethod(Point point1,Point point2){int x ,y,d,times1,times2,stepX,stepY; //k表示斜率int a,b,c; //a,b ,c分别为直线方程 aX+bY+c=0的参数int i;float k;x=point1.x; y=point1.y;times1=abs(point1.x-point2.x);//循环次数times2=abs(point2.y-point1.y);a=point2.y-point1.y; //求出直线方程 aX+bY+c=0的参数的参数ab=point1.x-point2.x; //求出直线方程 aX+bY+c=0的参数的参数bc=point1.x*(point1.y-point2.y)+point1.y*(point2.x-point1.x); //求出直线方程 aX+bY+c=0的参数的参数cstepX=b/abs(b)*(-1); //stepX表示该直线在X轴上的延伸方向，stepX值为1,表示直线像素点的横坐标跳步的方向与x轴一样，否则为-1 stepY=a/abs(a); //stepY表示该直线在y轴上的延伸方向，stepY 值为1,表示直线像素点的纵坐标跳步的方向与Y轴一样，否则为-1k=((float)a)/((float)b)*(-1); //求出斜率kglPointSize(1.0f);glBegin(GL_POINTS);if((0<=k)&&(k<=1)) //斜率为0到1的情况{d=a+0.5*b; //初值for(i=0;i<=times1;i++){x=x+stepX;if(stepX*d>=0) //判断y方向是否走步，stepX表示该直线在X轴上的延伸方向，stepX值为1,表示直线像素点的横坐标跳步的方向与x轴一样，否则为-1 //{y+=stepY;d=d+a+b;}elsed=d+a;glVertex2i(x,y);}}else if((1<k)&&(k<=10000)) //斜率大于1的情况{d=b+0.5*a;for(i=0;i<times2;i++) //times表示循环要执行的次数{y+=stepY;if(d*stepY<=0) //判断中点是否在直线的上方，stepY表示该直线在y轴上的延伸方向，stepX值为1,表示直线像素点的纵坐标跳步的方向与x轴一样，否则为-1{x+=stepX;d=d+a+b;}else d=d+b;glVertex2i(x,y);}}else if((-1<=k)&&(k<0)) //斜率为-1到0的情况{d=a+0.5*b;for(i=0;i<=times1;i++){x=x+stepX;if(stepX*d<=0){y+=stepY;d=d+a-b;}elsed=d+a;glVertex2i(x,y);}}else if((-10000<=k)&&(k<-1)) //斜率为小于-1的情况{d=a*0.5+b;for(i=0;i<=times2;i++){y=y+stepY;if(stepY*d>=0){x+=stepX;d=d-a+b;}elsed=d+b;glVertex2i(x,y);}}else //斜率无限大的情况{for(i=0;i<times2;i++){y+=1;glVertex2i(x,y);}}glEnd();}2、实验报告；报告中包含以下内容：①自己编写的绘图函数及其辅助函数。

OpenGL中点Bresenham绘制直线算法本⽂实例为⼤家分享了OpenGL中点Bresenham绘制直线算法，供⼤家参考，具体内容如下环境macos xcode编译器代码#include <GLUT/GLUT.h>#include <iostream>#include<iostream>#include<cstdlib>#include<ctime>using namespace std;float wid = 400; //设置窗⼝的⼤⼩,约定窗⼝必须为正⽅形float height = wid; //设置窗⼝的⼤⼩int numbers = 20; //设置划分的⽹格的个数float t = wid/numbers; //模拟像素下的单位1/*参数设置说明：输⼊直线的两点A(x1,y1);B(x2,y2)您应当确保参数范围在-400～400.且为整数。

*⽀持不同斜率*⽀持两点位置颠倒*/int x1 = -300,y1=-400,x2 =400,y2 = 100;void draw_point(float x, float y,int k_kind,int d_kind);float translater(int x);void swap(int &a, int &b){ int tmp = 0;tmp = b;b = a;a = tmp; }void bresenham(int x1, int y1,int x2, int y2){/*函数说明：bresenham算法部分参数说明：与openGL已有的划线函数⼀样，要求⽤户提供的是点的起点（x1,y1）和终点(x2,y2)为了便于观察，我们会绘制原像素下的直线。

这⾥的坐标要求是-1 ～ 1*/int k_kind = 0; //k_kind⽤来表⽰斜率的类型。

0是0～1；1是1～⽆穷；2是0～-1；3是负⽆穷～-1int d_kind =0; //d_kind⽤来表⽰dy正负的类型。

python语言实现的bresenham算法Bresenham算法是一种用于绘制直线的经典算法，它能够有效地计算出直线上的像素点，减少了计算与绘制的开销。

本文将逐步介绍如何使用Python语言实现Bresenham算法。

第一步，我们需了解Bresenham算法的原理及其背后的数学思想。

该算法基于直线的一般方程y = mx + b，其中m为斜率，b为y轴截距。

Bresenham算法的核心在于决策，即在每一个像素点处，选择最合适的下一个像素点。

其思想是，在给定的直线段中，比较由当前像素点到两个候选像素点的斜率值，从而决定下一步绘制的方向。

利用整数计算，避免了实数运算，提高了运行效率。

接下来，我们将使用Python语言实现Bresenham算法。

首先，需要引入必要的图形库，如matplotlib或者pygame。

这些库能够帮助我们在屏幕上绘制图形。

以matplotlib为例，我们首先需要创建一个画布，并在画布上绘制直线。

代码如下：pythonimport matplotlib.pyplot as plt# 创建画布fig, ax = plt.subplots()# 绘制直线def bresenham(x1, y1, x2, y2): dx = abs(x2 - x1)dy = abs(y2 - y1)if x1 < x2:sx = 1else:sx = -1if y1 < y2:sy = 1else:sy = -1err = dx - dywhile True:ax.plot(x1, y1, 'bo')if x1 == x2 and y1 == y2:breake2 = 2 * errif e2 > -dy:err = err - dyx1 = x1 + sxif e2 < dx:err = err + dxy1 = y1 + sy# 调用函数绘制直线bresenham(1, 1, 10, 8)# 显示画布plt.show()在上述代码中，我们首先创建了一个画布，并用`fig, ax = plt.subplots()`语句生成对应的`figure`和`axes`。

注：1、实验报告的内容: 一、实验目的；二、实验原理；三、实验步骤；四、实验结果；五、讨论分析（完成指定的思考题和作业题）；六、改进实验建议。

2、各专业可在满足学校对实验教学基本要求的前提下，根据专业特点自行设计实验报告的格式，所设计的实验报告在使用前需交实践教学管理科备案。

五、实验步骤1、复习有关直线扫描转换算法的基本原理，明确实验目的和要求；2、依据算法思想，绘制程序流程图；3、设计程序界面，要求操作方便；4、用C/C++语言编写源程序并调试、执行；5、分析实验结果6、对程序设计过程中出现的问题进行分析与总结；7、打印源程序或把源程序以文件的形式提交；8、按格式要求完成实验报告。

六、实验报告要求：1、各种算法的基本原理；2、各算法的流程图3、实验结果及分析（比较三种算法的特点，界面插图并注明实验条件）4、实验总结（含问题分析及解决方法）七、实验原理1、DDA算法(数值微分法)数值微分法(DDA法，Digital Differential Analyzer)是一种直接从直线的微分方程生成直线的方法。

给定直线的两端点P0(x0, y0)和P1(x1, y1)，得到直线的微分方程如下：DDA算法原理：由于直线的一阶导数是连续的，而且对于△x和△y是成正比的，故此可以通过在当前位置上分别加上二个小增量来求下一点的x，y坐标，如下图所示。

则有：其中，ε=1/max(|△x|,|△y|)分两种情况讨论如下：（1）max(|△x|,|△y|)=|△x|，即|k|≤1的情况：（2）max(|△x|,|△y|)=|△y|，此时|k|≥1：注意：由于在光栅化的过程中不可能绘制半个像素点，因此对求出的xi+1，yi+1的值需要四舍五入。

2、中点Bresenham算法给定直线的两个端点坐标，可以得到直线的方程为：此时直线将平面分成三个区域：对于直线上的点，F(x, y)=0；对于直线上方的点，F(x, y)>0；对于直线下方的点，F(x, y)<0，如下图所示。

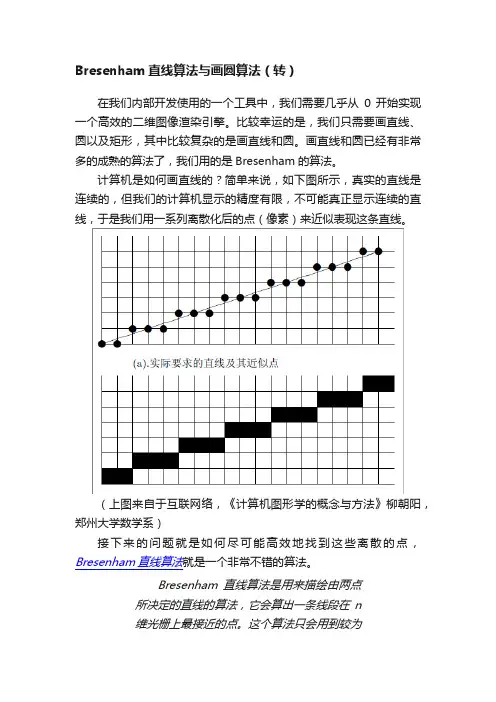
Bresenham直线算法与画圆算法（转）在我们内部开发使用的一个工具中，我们需要几乎从0 开始实现一个高效的二维图像渲染引擎。

比较幸运的是，我们只需要画直线、圆以及矩形，其中比较复杂的是画直线和圆。

画直线和圆已经有非常多的成熟的算法了，我们用的是Bresenham的算法。

计算机是如何画直线的？简单来说，如下图所示，真实的直线是连续的，但我们的计算机显示的精度有限，不可能真正显示连续的直线，于是我们用一系列离散化后的点（像素）来近似表现这条直线。

（上图来自于互联网络，《计算机图形学的概念与方法》柳朝阳，郑州大学数学系）接下来的问题就是如何尽可能高效地找到这些离散的点，Bresenham直线算法就是一个非常不错的算法。

Bresenham直线算法是用来描绘由两点所决定的直线的算法，它会算出一条线段在n维光栅上最接近的点。

这个算法只会用到较为快速的整数加法、减法和位元移位，常用于绘制电脑画面中的直线。

是计算机图形学中最先发展出来的算法。

(引自wiki 百科布雷森漢姆直線演算法)这个算法的流程图如下：可以看到，算法其实只考虑了斜率在 0 ~ 1 之间的直线，也就是与 x 轴夹角在 0 度到 45 度的直线。

只要解决了这类直线的画法，其它角度的直线的绘制全部可以通过简单的坐标变换来实现。

下面是一个C 语言实现版本。

1 2 3 4 5 // 交换整数 a 、b 的值inline void swap_int(int *a, int *b) {*a ^= *b;*b ^= *a;*a ^= *b;6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 }// Bresenham's line algorithmvoid draw_line(IMAGE *img, int x1, int y1, int x2, int y2, unsigned long c) {// 参数 c 为颜色值int dx = abs(x2 - x1),dy = abs(y2 - y1),yy = 0;if (dx < dy) {yy = 1;swap_int(&x1, &y1);swap_int(&x2, &y2);swap_int(&dx, &dy);}int ix = (x2 - x1) > 0 ? 1 : -1,iy = (y2 - y1) > 0 ? 1 : -1,cx = x1,cy = y1,n2dy = dy * 2,n2dydx = (dy - dx) * 2,d = dy * 2 - dx;if (yy) { // 如果直线与 x 轴的夹角大于 45 度while (cx != x2) {if (d < 0) {d += n2dy;} else {cy += iy;d += n2dydx;}putpixel(img, cy, cx, c);cx += ix;}} else { // 如果直线与 x 轴的夹角小于 45 度while (cx != x2) {if (d < 0) {d += n2dy;} else {cy += iy;d += n2dydx;}50515253putpixel(img, cx, cy, c);cx += ix;}}}可以看到，在画线的循环中，这个算法只用到了整数的加法，所以可以非常的高效。

编程实现bresenham直线扫描生成算法bresenham直线扫描生成算法是通过像素的光栅显示和扫描转换算法来画出直线的算法，这种算法能够用最少的计算量来在任意一个像素点中完成直线的绘制。

Bresenham有着广泛的应用，因为它是强力而有效的。

它其中它最常用于计算机图形学中用于绘制矢量图形。

在讨论具体实现之前，必须弄清楚所需要解决的基本问题。

bresenham直线扫描生成算法需要实现以下3步骤：1. 从起点到终点用步进方式移动；2. 确定像素点的位置；3. 对所有的像素点进行计算。

从实现的角度考虑，bresenham直线生成算法可以按照以下几个步骤来实现：1. 从起点开始，计算直线斜率，使用步长deltaX和deltaY来确定两个像素点的间距；2. 计算两个像素点在x-轴上的距离，用deltaX和deltaY来确定像素点的位置，并且求出它们在y-轴上的距离；3. 计算当前像素点处的梯度，以及梯度的变化度；4. 根据第2步计算得到的deltaX和deltaY，求出当前像素点处的误差值；5. 根据第3步和第4步计算得到的梯度和误差值，确定下一个像素点的位置，不断迭代，直至到达终点（两个像素点的距离小于等于1）；6. 绘制出直线。

不管是正斜率直线还是负斜率直线，都可以使用bresenham直线算法来实现。

具体实现时，我们需要声明两个变量deltaX和deltaY，分别根据步长计算点P(x,y)处误差值dx 和dy。

我们需要对dx和dy进行比较，若dx>dy，则每次跨x轴取整累加1,而每次跨y轴取float，反之取整只累加，这样从零开始就可以得到下一个要绘制的像素点。

总的来说，bresenham直线扫描生成算法是在直线的代价最优的情况下计算最优的像素点的位置，从而实现直线的绘制。

经过广泛的使用，Bresenham法已经得到了广泛的接受，并受到了越来越多的使用。

实现绘制各种情况直线的Bresenham算法，并将实现的算法应用于任意多边形的绘制，要求多边形的顶点由键盘输入或鼠标拾取，绘制的多边形顶点要准确，图形应该封闭。

要求掌握Bresenham算法的基本原理和算法设计，画出算法实现的程序流程图，使用C或者VC++实现算法，并演示。

-Implementation of the Bresenham line drawing algorithm for various situations, and to achieve an arbitrary polygon rendering algorithm is applied to require the polygon vertices from the keyboard input or mouse pick up and draw the polygon vertices to accurately, graphics should be closed. Bresenham algorithm required to master the basic theory and algorithm design, draw algorithm flow chart of procedures for the use of C or VC++ algorithm, and demonstrate.文件列表(点击判断是否您需要的文件，如果是垃圾请在下面评价投诉):ii\Debug\ii.exe..\.....\ii.ilk..\.....\ii.obj..\.....\ii.pch..\.....\ii.pdb..\.....\ii.res..\.....\iiDoc.obj..\.....\iiView.obj..\.....\MainFrm.obj..\.....\StdAfx.obj..\.....\vc60.idb..\.....\vc60.pdb..\ii.cpp..\ii.dsp..\ii.dsw..\ii.h..\ii.ncb..\ii.opt..\ii.plg..\ii.rc..\iiDoc.cpp..\iiDoc.h..\iiView.cpp ..\iiView.h..\MainFrm.cpp ..\MainFrm.h ..\ReadMe.txt ..\res\ii.ico..\...\ii.rc2..\...\iiDoc.ico ..\...\Toolbar.bmp ..\Resource.h ..\StdAfx.cpp..\Debug ..\resii。