扫描线算法
- 格式:ppt
- 大小:1.00 MB
- 文档页数:52

基于扫描线的线段求交算法扫描线算法是一种计算线段交点的常用方法。
它的基本思想是,将二维空间中的线段拆分成多个水平线段,然后通过遍历扫描线的方式,将每条扫描线与线段进行求交。
具体实现上,我们可以按照以下步骤进行:1.线段拆分:将给定的线段按照两端点的纵坐标从小到大进行排序,将线段分割成多个水平线段。
每个水平线段由一个起点和一个终点组成,起点的y值小于终点的y值。
2.扫描线初始化:将扫描线从最小的y值开始,以步长为1沿着y轴向上移动。
3.当前线段集合初始化:将与当前扫描线y值相交的水平线段添加到当前线段集合中。
4.求交点:遍历当前线段集合,将相邻的水平线段进行求交,得到所有线段交点。
5.更新当前线段集合:将终点y值小于当前扫描线y值的水平线段从当前线段集合中移除。
6.更新扫描线:将扫描线向上移动一个步长。
7.重复步骤3-6,直到扫描线超过最大的y值,并且当前线段集合为空。
在该算法中,关键的步骤是求交点的过程。
可以使用一维直线相交的算法,如线性插值,来计算线段的交点。
扫描线算法的时间复杂度主要取决于线段的数量和扫描线的数量。
对于n个线段和m个扫描线,时间复杂度可以达到O(nlogn + m)。
这种算法广泛应用于计算机图形学中的线段裁剪、多边形填充等领域。
它的优点是简单易懂,实现相对容易,并且可以高效地处理大量的线段求交问题。
然而,扫描线算法在处理复杂的线段求交问题时可能会遇到一些挑战。
例如,当线段存在重叠或相交的情况时,需要特殊处理来确保交点的正确性。
此外,当线段的数量较多时,算法的时间复杂度可能会较高,导致计算效率下降。
总之,扫描线算法是一种经典的线段求交算法,通过拆分线段和遍历扫描线的方式,可以高效地计算出线段的交点。
在实际应用中,我们可以结合具体问题的特点,采用一些优化策略来提高算法的效率和稳定性。

扫描线算法(Scan-Line F illing)扫描线算法适合对矢量图形进行区域填充,只需要直到多边形区域的几何位置,不需要指定种子点,适合计算机自动进行图形处理的场合使用,比如电脑游戏和三维CAD软件的渲染等等。
对矢量多边形区域填充,算法核心还是求交。
《计算几何与图形学有关的几种常用算法》一文给出了判断点与多边形关系的算法――扫描交点的奇偶数判断算法,利用此算法可以判断一个点是否在多边形内,也就是是否需要填充,但是实际工程中使用的填充算法都是只使用求交的思想,并不直接使用这种求交算法。
究其原因,除了算法效率问题之外,还存在一个光栅图形设备和矢量之间的转换问题。
比如某个点位于非常靠近边界的临界位置,用矢量算法判断这个点应该是在多边形内,但是光栅化后,这个点在光栅图形设备上看就有可能是在多边形外边(矢量点没有大小概念,光栅图形设备的点有大小概念),因此,适用于矢量图形的填充算法必须适应光栅图形设备。
2.1扫描线算法的基本思想扫描线填充算法的基本思想是:用水平扫描线从上到下(或从下到上)扫描由多条首尾相连的线段构成的多边形,每根扫描线与多边形的某些边产生一系列交点。
将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜色画水平直线。
多边形被扫描完毕后,颜色填充也就完成了。
扫描线填充算法也可以归纳为以下4个步骤:(1)求交,计算扫描线与多边形的交点(2)交点排序,对第2步得到的交点按照x值从小到大进行排序;(3)颜色填充,对排序后的交点两两组成一个水平线段,以画线段的方式进行颜色填充;(4)是否完成多边形扫描?如果是就结束算法,如果不是就改变扫描线,然后转第1步继续处理;整个算法的关键是第1步,需要用尽量少的计算量求出交点,还要考虑交点是线段端点的特殊情况,最后,交点的步进计算最好是整数,便于光栅设备输出显示。
对于每一条扫描线,如果每次都按照正常的线段求交算法进行计算,则计算量大,而且效率底下,如图(6)所示:图(6)多边形与扫描线示意图观察多边形与扫描线的交点情况,可以得到以下两个特点:(1)每次只有相关的几条边可能与扫描线有交点,不必对所有的边进行求交计算;(2)相邻的扫描线与同一直线段的交点存在步进关系,这个关系与直线段所在直线的斜率有关;第一个特点是显而易见的,为了减少计算量,扫描线算法需要维护一张由“活动边”组成的表,称为“活动边表(AET)”。
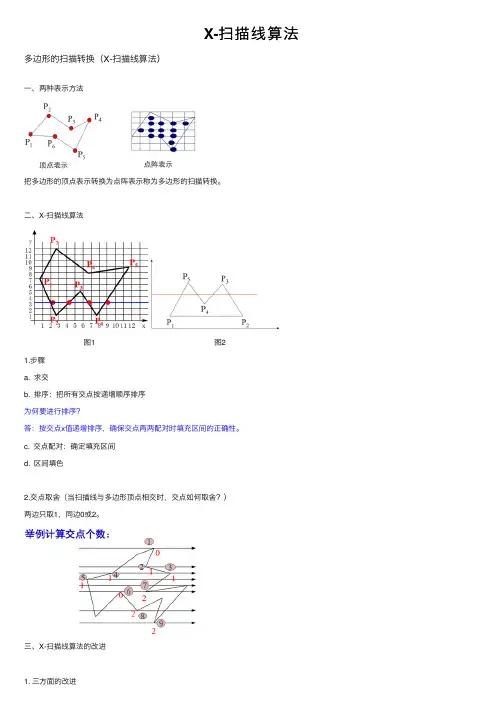
X-扫描线算法多边形的扫描转换(X-扫描线算法)⼀、两种表⽰⽅法把多边形的顶点表⽰转换为点阵表⽰称为多边形的扫描转换。
⼆、X-扫描线算法 图1 图21.步骤a. 求交b. 排序:把所有交点按递增顺序排序为何要进⾏排序?答:按交点x值递增排序,确保交点两两配对时填充区间的正确性。
c. 交点配对:确定填充区间d. 区间填⾊2.交点取舍(当扫描线与多边形顶点相交时,交点如何取舍?)两边只取1,同边0或2。
三、X-扫描线算法的改进1. 三⽅⾯的改进a. 处理⼀条扫描线,仅对与它相交的多边形的边(有效边)进⾏求交运算。
(也就是避免把所有的边都进⾏求交,因为⼤部分的边求交结果为空。
所以设置⼀个表来记录有效边。
即下⾯提到的AET)b. 考虑边的连贯性:当前扫描线与各边的交点顺序与下⼀条扫描线与各边的交点顺序很可能相同或⾮常相似。
c. 多边形的连贯性:当某条边与当前扫描线相交时,它很可能也与下⼀条扫描线相交。
2.数据结构通过引⼊新的数据结构来避免求交运算(1)活性边表a. 活性边表(AET):把和当前扫描线相交的边称为活性边,并把它们按交点x坐标递增的顺序存于⼀个链表中。
b. 结点内容Δx=1/k,y max 是为了知道何时达到边界c. 举例(2)新边表(NET)建⽴AET需要知道与哪些边相交,所以定义NET来存储边的信息,从⽽⽅便AET的建⽴。
a. 构造⼀个纵向链表,长度为多边形占有的最⼤扫描线数。
每个节点(称为吊桶)对应多边形覆盖的⼀条扫描线。
b. 结点内容y max:该边的y最⼤值x min:该边较低点的x坐标c. NET挂在与该边较低端y值相同的扫描线吊桶中此时NET也就记录了6条有效边(3)NET与AET的使⽤流程⾸先我们得明⽩,AET的⽬的是为了使⽤增量⽅法避免求交运算,⽽NET是⽤在构造AET的。
a. 所以第⼀步为构造NET。
⽅法:遍历所有扫描线,把y min = i 的边放进NET[ i ]中,从⽽构造出整个NET。

用扫描线算法实现多边形填充扫描线算法是一种用于多边形填充的有效方法。
它的思想是遍历扫描线,并在每条扫描线与多边形边界相交时填充相应的像素。
首先,我们需要了解多边形表示的方法。
多边形可以用一系列有序的边来表示,每条边由起点和终点坐标组成。
例如,一个三角形可以表示为三条线段的集合。
接下来,我们将介绍如何使用扫描线算法来实现多边形填充:1.首先,找到多边形的最大和最小y坐标,即多边形的上边界和下边界。
2.从上边界开始,逐条扫描线遍历到下边界。
3.在每条扫描线上,确定与多边形边界相交的线段。
4.根据与多边形边界相交的线段的起点和终点,找到对应的x坐标范围。
5.根据x坐标的范围,填充相应的像素。
下面是一个使用扫描线算法填充多边形的伪代码示例:```ScanLineFill(polygon):ymin = polygon.minYymax = polygon.maxYfor y from ymin to ymax:intersections = FindIntersections(polygon, y)sort(intersections)for i from 0 to length(intersections) - 1 by 2:xstart = intersections[i]xend = intersections[i+1]FillPixels(xstart, xend, y)```此伪代码的`FindIntersections`函数是用来找到多边形边界与当前扫描线相交的点,而`FillPixels`函数则用来填充相应的像素。
在实际实现时,可以使用一些数据结构来存储多边形的边界信息和扫描线与边界相交的点。
例如,可以使用边表来存储多边形的边界,使用活性边表来存储与当前扫描线相交的边界,使用扫描线来表示当前的扫描线位置。
算法的时间复杂度主要取决于扫描线与边界相交点的计算,可以通过使用边表和一些优化技巧来降低时间复杂度。

实验报告(扫描线算法)一、实验目的学习扫描线算法,掌握种子区域填充的程序设计方法。
二、实验原理A.多边形扫描转换根据区域的连贯性、扫描线的连贯性、边的连贯性以及奇点的处理方法,做出基于扫描线算法数据结构(ET&AEL )的扫描线算法程序。
其算法的实现步骤如下:1) (扫描线初始化)取扫描线纵坐标y 的初始值为ET 中非空元素的最小序号。
(对给定的多边形,y=constant );2) (AEL 初始化)将边的活化链表AEL 置为空表;3) 按从下到上的顺序对纵坐标值为y 的扫描线执行以下操作,指导边的分类表ET 和边的活化链表AEL 为空表为止;①若ET 中第y 类元素非空,则将属于该类的所有边从ET 中取出并插入到AEL 中。
AEL 中的各边按照x 的值(当x 值相等时,按x ∆值)递增的顺序排序。
②若相对当前扫描线,AEL 非空,则将AEL 中的边两两配对。
即第1、2边为一对,第3、4边为一对,以此类推。
每一对边与当前扫描线的交点所构成的区段位于多边形内。
依次对这些区段上的像素点按多边形颜色着色。
③将AEL 中满足条件y y =max 的边删去。
④将AEL 中剩余的每一条边的x 域累加x ∆,即x x x ∆+=。
⑤将当前扫描线的纵坐标值y 累加1,即y y y ∆+=。
B.多边形的填充(边界标志算法)先用一种特殊颜色在帧缓冲器中将多边形的边界(水平边界除外)勾画出来,然后再用类似扫描线算法的方法对于多边形内的各区段着上所需颜色。
三、实验程序//A.多边形扫描转换#include<stdio.h>#include<graphics.h>#include<easyx.h>#include<conio.h>#define YMAX 480 /*宏定义*/typedef struct tEdge //定义结构体{int yUpper,yLower;float xIntersect,dxPerScan;struct tEdge *next;struct tEdge *active;}Edge;void insertEdge (Edge *list,Edge *edge) //将结点插入边表{Edge *p,*q=list;p=q->next;while (p!=NULL){if(edge->xIntersect<p->xIntersect)p=NULL;else{q=p;p=p->next;}}edge->next=q->next;q->next=edge;}int yNext (int k,int count,int *y) //求奇异点{int j;if((k+1)>(count-1))j=0;elsej=k+1;while(y[k]==y[j])if((j+1)>(count-1))j=0;elsej++;return(y[j]);}void makeEdgeRecord(int xLower,int yLower,int xUpper,int yUpper,int yComp,Edge *edge,Edge *edges[])//生成边表结点,并插入到边表中{edge->dxPerScan=(float)(xUpper-xLower)/(yUpper-yLower);edge->yUpper=yUpper;if(yLower>yComp){edge->yLower=yLower+1;edge->xIntersect=xLower+edge->dxPerScan;}elseedge->xIntersect=(float)xLower;insertEdge(edges[yLower],edge);}void buildEdgeList(int count,int *x,int *y,Edge *edges[]) //创建边表的主体函数{Edge *edge;int x1,y1,x2,y2;int i,yPrev=y[count-2];x1=x[count-1];y1=y[count-1];for(i=0;i<count;i++){x2=x[i];y2=y[i];if(y1!=y2){edge=(Edge *)malloc(sizeof(Edge));if(y1<y2)makeEdgeRecord(x2,y2,x1,y1,yNext(i,count,y),edge,edges);elsemakeEdgeRecord(x1,y1,x2,y2,yPrev,edge,edges);}yPrev=y1;x1=x2;y1=y2;}}void buildActiveList(int scan,Edge *active,Edge *edges[]) //建立活动边表的主体函数{Edge *p,*q;p=edges[scan]->next;while(p){q=p->next;insertEdge(active,p);p=q;}}void fillScan(int scan,Edge *active) //填充当前扫描线{Edge *p1,*p2;int i,PolygonColor=25;p1=active->next;while(p1);{p2=p1->next;for(i=(int)p1->xIntersect;i<p2->xIntersect;i++)putpixel(i,scan,PolygonColor);p1=p2->next;}}void deleteAfter(Edge *q) //删除已经处理过的边{Edge *p=q->next;q->next=p->next;free(p);}void updateActiveList(int scan,Edge *active) //更新活化链表{Edge *q=active,*p=active->next;while (p)if(scan>=p->yUpper){p=p->next;deleteAfter(q);}else{p->xIntersect=p->xIntersect+p->dxPerScan;q=p;p=p->next;}}void resortActiveList(Edge *active) //活化链表排序{Edge *q, *p=active->next;while(p){q=p->next;insertEdge(active,p);p=q;}}void scanFillPolygon(int count,int *x,int *y) //多边形扫描转换{Edge *edges[YMAX],*active;int i,scan;//扫描线的边界for(i=0;i<YMAX;i++){edges[i]=(Edge *)malloc(sizeof(Edge));//申请空间edges[i]->next=NULL;}buildEdgeList( count, x, y, edges);active=(Edge *)malloc(sizeof(Edge));active->next=NULL;//初始化边表for(scan=0;scan<YMAX;scan++){buildActiveList(scan,active,edges);if (active->next){fillScan(scan,active);updateActiveList(scan,active);resortActiveList(active);}}free(active);}void main(){int gdriver = DETECT,gmode;initgraph(700,600); //初始化窗口大小int x[]={240,390,540,232};int y[]={150,230,430,370};int count=4;line(240,150,390,230);line(390,230,540,430);line(540,430,232,370);line(232,370,240,150);scanFillPolygon(count,x,y);getch();//暂停程序closegraph();//退出图形库}//B.多边形的填充(失败)四、测试结果A.多边形扫描转换B.多边形的填充(失败)。

扫描线算法(Scan-Line F illing)扫描线算法适合对矢量图形进行区域填充,只需要直到多边形区域的几何位置,不需要指定种子点,适合计算机自动进行图形处理的场合使用,比如电脑游戏和三维CAD软件的渲染等等。
对矢量多边形区域填充,算法核心还是求交。
《计算几何与图形学有关的几种常用算法》一文给出了判断点与多边形关系的算法――扫描交点的奇偶数判断算法,利用此算法可以判断一个点是否在多边形内,也就是是否需要填充,但是实际工程中使用的填充算法都是只使用求交的思想,并不直接使用这种求交算法。
究其原因,除了算法效率问题之外,还存在一个光栅图形设备和矢量之间的转换问题。
比如某个点位于非常靠近边界的临界位置,用矢量算法判断这个点应该是在多边形内,但是光栅化后,这个点在光栅图形设备上看就有可能是在多边形外边(矢量点没有大小概念,光栅图形设备的点有大小概念),因此,适用于矢量图形的填充算法必须适应光栅图形设备。
扫描线算法的基本思想扫描线填充算法的基本思想是:用水平扫描线从上到下(或从下到上)扫描由多条首尾相连的线段构成的多边形,每根扫描线与多边形的某些边产生一系列交点。
将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜色画水平直线。
多边形被扫描完毕后,颜色填充也就完成了。
扫描线填充算法也可以归纳为以下4个步骤:(1)求交,计算扫描线与多边形的交点(2)交点排序,对第2步得到的交点按照x值从小到大进行排序;(3)颜色填充,对排序后的交点两两组成一个水平线段,以画线段的方式进行颜色填充;(4)是否完成多边形扫描?如果是就结束算法,如果不是就改变扫描线,然后转第1步继续处理;整个算法的关键是第1步,需要用尽量少的计算量求出交点,还要考虑交点是线段端点的特殊情况,最后,交点的步进计算最好是整数,便于光栅设备输出显示。
对于每一条扫描线,如果每次都按照正常的线段求交算法进行计算,则计算量大,而且效率底下,如图(6)所示:图(6)多边形与扫描线示意图观察多边形与扫描线的交点情况,可以得到以下两个特点:(1)每次只有相关的几条边可能与扫描线有交点,不必对所有的边进行求交计算;(2)相邻的扫描线与同一直线段的交点存在步进关系,这个关系与直线段所在直线的斜率有关;第一个特点是显而易见的,为了减少计算量,扫描线算法需要维护一张由“活动边”组成的表,称为“活动边表(AET)”。

扫描线算法先从⼀道模板题⼊⼿吧..这道题需要我们求n个矩形的⾯积并。
~~ 数据还很变态 ~~给出这n的矩形的左下⾓和右上⾓坐标,~~ ≤10^9 只能⽤离散化,离散化之后最多到n也就是10^5,能够维持。
怎么做?for循环?T(LE)M(LE)⼤套餐等着你离散化之后循环都要超时还存不下 ~~先把所有的⾯积相加再减去重复?~~ 现实点,你做不到 ~~扫描线算法基础就是应对这种问题的。
它的思想是分割图形⽐如说,有n个矩形组成这张图。
我们设想,有⼀条⽆限长度的竖线⾃左往右扫过这⼀⽚图形。
只保留这些矩形被竖线扫到的左右两条线段,组成包含2*n条线段的⼀张图。
对于每个矩形,把左边那条线段记为+1,右边的记为-1.像这样:对于两两相邻的部分,我们可以分别计算⾯积,这样就得到了整个并集图形的⾯积。
怎么记录这⼀条条线段?结构体。
要存储的东西有:这条竖线段的横坐标,上下端点的竖坐标,以及1/-1(记录是左还是右)按照题⽬表述记为:{x,y1,y1,1/-1}显然,我们只要把这些线的横坐标拿来排序,对于⼀次遍历来说,每对对应线段之间的距离是已知的,那么我们需要解决的问题只有纵坐标的影响范围。
不妨把所有纵坐标都取出来,离散化映射到[1,t]的区间中的t的整数值,并把这些纵坐标表⽰为t-1段,其中第i段表⽰第i个纵坐标和第i+1个纵坐标之间的部分,然后⽤c[i]表⽰第i段被覆盖的次数。
这样就可以计算⾯积并,算法流程⼤致是这样:对于每⼀个线段,将其的k值累加到这个线段对应的若⼲个纵坐标区间计算⾯积:所有T−1个纵坐标区间对应的c值⼤于零的就说明这些部分的区间还存在,将存在的区间的长度累加起来,乘上当前线段与下⼀条线段之间的横坐标之差就是这两条线段之间的⾯积。
显然,这⾥就需要⽤到区间求和的操作。
这种事情,就丢给线段树吧!因为这道题中的区间修改都是成对出现的(+1/-1),所以不需要懒标记这个操作。
只需要在线段树的每个端点多维护两个值:cnt和len,分别记这段区间被覆盖的次数以及当前区间的纵坐标长度。

区域填充的扫描线算法区域填充是一种常见的计算机图形学算法,用于将一个封闭区域内的所有像素点填充为指定的颜色。
扫描线算法是区域填充的一种常用方法,本文将介绍扫描线算法的基本原理、实现步骤和一些优化技巧。
扫描线算法的基本原理是利用扫描线从图像的上边界向下扫描,检测每个扫描线与区域的交点。
当遇到一个交点时,根据该交点的左右两侧的交点情况,确定将该交点连接到哪个交点上。
通过不断地扫描和连接交点,最终将整个区域填充为指定的颜色。
下面是扫描线算法的具体实现步骤:1.首先需要确定区域的边界,可以由用户提供或通过其他算法生成。
边界可以用一系列的线段、多边形或曲线表示。
2. 创建一个数据结构来存储每个扫描线与区域的交点。
常用的数据结构是活性边表(Active Edge Table,AET)和扫描线填充表(Scanline Fill Table,SFT)。
AET用于存储当前扫描线与区域边界的交点,SFT用于存储所有扫描线的交点。
3.初始化扫描线的起始位置为图像的上边界,并创建一个空的AET。
4.开始扫描线的循环,直到扫描线到达图像的下边界。
每次循环都进行以下操作:-将扫描线与区域边界进行相交,找出所有与区域相交的线段,并将它们的交点加入到AET中。
-对AET按照交点的x坐标进行排序。
-从AET中取出相邻的两个交点,根据这两个交点之间的像素点是否在区域内来决定是否填充这些像素点。
5.当扫描线到达图像的下边界时,完成填充。
扫描线算法的实现可能会遇到一些边界情况和优化需求。
下面是一些常见的优化技巧:1.边界处理:在AET中存储的交点需要进行边界处理,确保交点处于图像范围内。
2.垂直线段处理:对于垂直线段,可以进行特殊处理,避免在AET中重复存储相同的交点。
3.区域内部边界处理:当区域内部有不连续的边界时,需要对交点进行合并,避免出现多余的像素点填充。
4.使用扫描线填充算法优化:对于大尺寸的区域填充,可以使用扫描线填充算法进行优化。

计算机图形学——区域填充的扫描线算法一.实验名称:区域填充的扫描线算法二.实验目的:1、理解区域填充扫描线算法的原理;2、实现区域填充的扫描线算法并测试;三.算法原理:算法基本思想: 首先填充种子点所在扫描线上位于区域内的区段,然后确定与该区段相邻的上下两条扫描线上位于区域内的区段,并依次将各区段的起始位置保存, 这些区段分别被用区域边界色显示的像素点所包围。
随后,逐步取出一开始点并重复上述过程,直到所保存各区段都填充完毕为止。
借助于栈结构,区域填充的扫描线算法之步骤如下:Step 1. 初始化种子点栈:置种子点栈为空栈,并将给定的种子点入栈;Step 2. 出栈:若种子点栈为空,算法结束;否则,取栈顶元素(x,y)为种子点;Step 3. 区段填充:从种子点(x, y) 开始沿纵坐标为y 的当前扫描线向左右两个方向逐像素点进行填色,其颜色值置为newcolor 直至到达区域边界。
分别以xl 和xr 表示该填充区段两端点的横坐标;Step 4. 新种子点入栈: 分别确定当前扫描线上、下相邻的两条扫描线上位于区段[xl, xr] 内的区域内的区段。
若这些区段内的像素点颜色值为newolor ,则转至Step 2;否则以区段的右端点为种子点入种子点栈,再转至Step 2。
四.原程序代码:/*****************************************//*4-ScanLineFill 区域填充的扫描线算法实现*//*****************************************/#include <stdio.h>#include <conio.h>#include <graphics.h>#include <malloc.h>#define Stack_Size 100 //栈的大小常量//定义结构体,记录种子点typedef struct{int x;int y;}Seed;//定义顺序栈(种子点)typedef struct{Seed Point[Stack_Size];int top;}SeqStack;//初始化栈操作void InitStack(SeqStack *&S){S=(SeqStack *)malloc(sizeof(SeqStack));S->top=-1;}//种子点栈置空;void setstackempty (SeqStack *S){S->top==-1;}//种子点栈状态检测函数int isstackempty (SeqStack *S){if(S->top==-1)return true; //空栈返回trueelsereturn false; //非空栈返回false}//种子点入栈;int stackpush (SeqStack *&S,Seed point){if(S->top==Stack_Size-1)//栈已满,返回false return false;S->top++;//栈未满,栈顶元素加1S->Point[S->top]= point;return true;}//取栈顶元素;int stackpop (SeqStack *&S,Seed &point){if(S->top==-1)//栈为空,返回falsereturn false;point=S->Point[S->top];S->top --;//栈未空,top减1return true;}//画圆void CirclePoints (int xc, int yc, int x, int y, int Color) {putpixel (xc + x, yc + y, Color);putpixel (xc + x, yc - y, Color);putpixel (xc - x, yc + y, Color);putpixel (xc - x, yc - y, Color);putpixel (xc + y, yc + x, Color);putpixel (xc + y, yc - x, Color);putpixel (xc - y, yc + x, Color);putpixel (xc - y, yc - x, Color); }//中点画圆算法void MidpointCircle(int radius, int Color) {int x, y;float d;x=0;y=radius;d=5.0/4-radius;CirclePoints(250,250,x,y,Color);while(x<y){if (d<0){d+=x*2.0+3;}else{d+=(x-y)*2.0+5;y--;}x++;CirclePoints(250,250,x,y,Color);}}//四连通扫描线算法void ScanLineFill4(int x, int y, int oldcolor, int newcolor) {int xl, xr, i;bool SpanNeedFill;Seed pt;//种子点SeqStack *S;//定义顺序栈InitStack(S);//定义了栈之后必须把栈先初始化setstackempty(S);//种子点栈置空;pt.x = x;pt.y = y;stackpush (S,pt); // 种子点(x, y)入栈while (!isstackempty(S)){stackpop (S,pt);//取种子点y = pt.y;x = pt.x;while (getpixel (x,y)==oldcolor) {// 从种子点开始向右填充putpixel (x, y, newcolor);x++;}xr = x -1;x = pt.x -1;while (getpixel (x,y)==oldcolor) { // 从种子点开始向左填充putpixel (x, y, newcolor);x--;}xl = x + 1;x = xl;y = y +1; // 处理上面一条扫描线while (x < xr){SpanNeedFill = false;while (getpixel (x, y)==oldcolor){SpanNeedFill = true;x++ ;} // 待填充区段搜索完毕if (SpanNeedFill){// 将右端点作为种子点入栈pt.x = x - 1;pt.y = y;stackpush (S,pt);SpanNeedFill = false;} //继续向右检查以防遗漏while ((getpixel (x, y)!=oldcolor) && (x< xr)) x++;} //上一条扫描线上检查完毕x = xl;y=y-2; // 处理下面一条扫描线while (x < xr){SpanNeedFill = false;while (getpixel (x, y)==oldcolor){SpanNeedFill=true;x++ ;}if (SpanNeedFill){pt.x= x - 1;pt.y = y;stackpush (S,pt);SpanNeedFill=false;}while ((getpixel (x, y)!=oldcolor) && (x < xr))x++;}}}//主函数检测void main(){int radius,color;int x,y;//种子点int oldcolor,newcolor;//原色与填充色//输入参数值printf("input radius and color:\n");//画圆参数scanf("%d,%d",&radius,&color);printf("input x and y:\n"); //读入内点scanf("%d,%d", &x, &y);printf("input oldcolor and newcolor:\n"); //读入原色与填充色scanf("%d,%d", &oldcolor, &newcolor);int gdriver = DETECT,gmode;initgraph(&gdriver, &gmode, "c:\\tc");// 用背景色清空屏幕cleardevice();// 设置绘图色为红色setcolor(RED);MidpointCircle(radius,color);//用中点画圆算法画圆rectangle(150, 150, 350, 350);//再画一个矩形区域ScanLineFill4 (x,y,oldcolor,newcolor);//扫描线区域填充getch();closegraph();}五.运行结果与讨论:测试结果1:测试结果2:六.实验分析与讨论:1.通过借助栈这一数据结构,完成了区域填充的扫描线算法的实现,并利用以前所学的画圆等算法,进行综合运用,在此基础上进行扩充,设计多种图案,进行扫描线填充算法的检测,都得到了理想的结果,体现了算法的有效性;2.栈的数据结构给种子点的操作带来了极大的方便,为算法的实现提供了便利,同时还提高了算法的复用性和可靠性;3.此扫描线填充算法能够对多种图案进行填充,展现了算法的实用性。

扫描线区域填充算法
扫描线区域填充算法,又称为"扫描线填涂算法",它用于对平面中特定区域填充指定的颜色、灰度或纹理,是计算机图形学中常用的算法之一。
该算法的原理是:给定待填充的区域内的点的有限个边界,从某一顶点开始,以某一规则遍历所有的边界点,形成边界数组,接着顺次扫描边界数组,将包含在边界中的每个合理像素点标记成已填充状态,由此而达到填充区域的目的。
算法步骤如下:
(1)设置起始点A,判断是否存在右方向上有没有边界点,若有,则把下一个边界点B作为起始点;
(2)从起始点A 开始,以扫描线的形式一次扫描边界点,把有效的像素点标记为“已填充”;
(3)把已扫描的点加入边界数组,直到下一个边界点C,且C点不等于起始点A;
(4)重复步骤(2)和(3),直至再回到起始点A,完成一次区域填充;
(5)如果还有未填充的区域,则重复步骤(1)至(4),直至所有区域填充完成。
实际应用中,为了避免停滞,可以采用八方向搜索策略;此外,由于扫描线填充算法中填充空间的范围是由边界点定义的,因此,当边界未经处理的是孤立的点或直线时,将无法实现实际的填充效果。
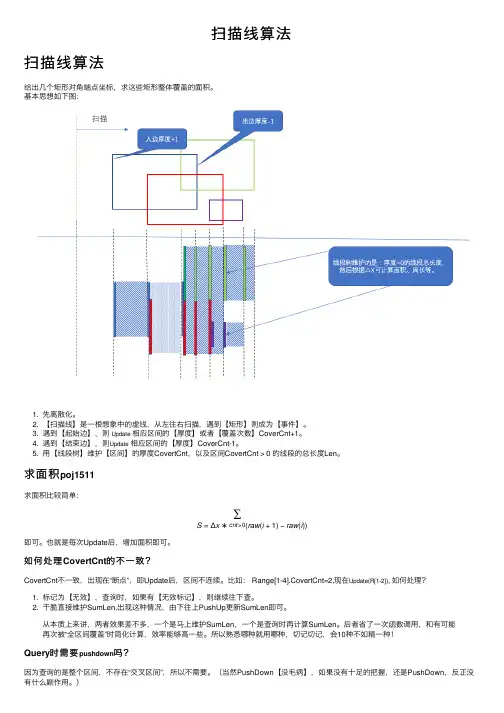
扫描线算法扫描线算法给出⼏个矩形对⾓端点坐标,求这些矩形整体覆盖的⾯积。
基本思想如下图:1. 先离散化。
2. 【扫描线】是⼀根想象中的虚线,从左往右扫描,遇到【矩形】则成为【事件】。
3. 遇到【起始边】,则Update相应区间的【厚度】或者【覆盖次数】CoverCnt+1。
4. 遇到【结束边】,则Update相应区间的【厚度】CoverCnt-1。
5. ⽤【线段树】维护【区间】的厚度CovertCnt,以及区间CovertCnt > 0 的线段的总长度Len。
求⾯积poj1511求⾯积⽐较简单:S=Δx∗∑cnt>0(raw(i+1)−raw(i))即可。
也就是每次Update后,增加⾯积即可。
如何处理CovertCnt的不⼀致?CovertCnt不⼀致,出现在“断点”,即Update后,区间不连续。
⽐如: Range[1-4].CovertCnt=2,现在Update(R[1-2]), 如何处理?1. 标记为【⽆效】,查询时,如果有【⽆效标记】,则继续往下查。
2. ⼲脆直接维护SumLen,出现这种情况,由下往上PushUp更新SumLen即可。
从本质上来讲,两者效果差不多,⼀个是马上维护SumLen,⼀个是查询时再计算SumLen。
后者省了⼀次函数调⽤,和有可能再次被“全区间覆盖”时简化计算,效率能够⾼⼀些。
所以熟悉哪种就⽤哪种,切记切记,会10种不如精⼀种!Query时需要pushdown吗?因为查询的是整个区间,不存在“交叉区间”,所以不需要。
(当然PushDown【没⽑病】,如果没有⼗⾜的把握,还是PushDown,反正没有什么副作⽤。
)Query,当【查询区间】和【更新区间】出现【交叉】的时候,需要PushDown,⽐如:更新到:[1-2]和[3-4]但要查询[2-3],则只能由[2]``[3]两部分构成,所以你必须要从[1-2]PushDown到[2],从[3-4]pushdown到[3]。
实验三区域填充扫描线算法区域填充扫描线算法是一种计算机图形学算法,用于实现区域填充功能。
该算法通过扫描像素的方式,检测封闭区域内的每一条扫描线与区域边界的交点,并根据交点之间的像素颜色进行填充。
算法步骤如下:1.扫描线从画布的最底部开始,逐行向上移动。
2.检测扫描线与区域边界的交点,并记录交点的x坐标。
3.对于每对相邻的交点(称为活动边),按照交点的x坐标从左到右进行遍历。
4.遍历过程中,判断当前像素是否在封闭区域内。
如果在区域内,根据填充颜色进行颜色填充。
5.对于扫描线上的下一条扫描线,根据当前扫描线的活动边情况,更新活动边,即将下一条扫描线上的新交点加入到活动边中。
区域填充扫描线算法的优点在于其适用于任意形状的封闭区域,并且可以处理带有内部孔洞的区域。
相比其他填充算法,如扫描线填充算法,区域填充扫描线算法具有更好的效率和性能。
然而,区域填充扫描线算法也存在一些限制和问题。
首先,该算法要求区域边界是封闭的,并且必须采用逆时针顺序来定义区域内的边界。
其次,算法的实现和性能受到硬件设备的限制,特别是在处理较大尺寸的区域时可能出现性能问题。
为了解决这些问题,可以采用一些优化方法来改进算法的性能。
例如,可以使用空间填充曲线(Space Filling Curves)来加速扫描线的遍历过程。
还可以使用并行计算技术来加速算法的执行,特别是在处理大尺寸区域时。
总之,区域填充扫描线算法是一种常用的图形学算法,用于实现区域填充功能。
虽然具有一些限制和问题,但可以通过一些优化方法来改进算法的效率和性能,满足实际应用的需求。
扫描线区域填充算法算法步骤如下:1.找到图形区域的上下边界:-遍历图形的所有边界点,找到最大纵坐标和最小纵坐标,确定扫描线的上下边界。
2.初始化扫描线列表:-从上到下依次生成扫描线,建立一个扫描线列表。
3.计算扫描线与图形的交点:-遍历扫描线列表中的每个扫描线,与图形的所有边界进行求交。
-如果与边界有交点,将交点的横坐标存入一个集合中,集合中的数据按从小到大排序。
4.进行填充:-遍历扫描线列表中的每个扫描线,找到对应的交点集合。
-将集合中的每两个横坐标之间的像素点进行填充。
以下是对算法的详细解释:首先,我们需要遍历所有边界点,找到最大纵坐标和最小纵坐标。
这样就确定了我们需要扫描的区域范围,也就是扫描线的上下边界。
接下来,我们生成一个扫描线列表。
从上到下依次生成每一条扫描线,将其存储在扫描线列表中。
然后,对于每一条扫描线,我们需要计算该扫描线与图形的交点。
我们遍历图形的所有边界,并与当前扫描线进行求交。
如果与边界有交点,我们将交点的横坐标存入一个集合中。
这个集合中的数据按从小到大排序,以便后续的填充操作。
最后,我们对于每一条扫描线,找到对应的交点集合。
我们遍历集合中的每两个横坐标之间的像素点,将其进行填充。
这可以通过修改像素的颜色或设置像素的属性来实现。
总结一下,扫描线区域填充算法通过逐行扫描图形区域,计算每行与区域内部的交点,然后进行填充。
该算法的优点是简单、高效,适用于填充简单凸多边形等闭合图形。
然而,该算法对于非凸多边形或包含内孔的图形表现较差,可能需要额外的处理逻辑。
第章基本光栅图形算法(1)
第章基本光栅图形算法
本章节将介绍基本光栅图形算法的概念,包括扫描线算法、多边形填充算法和画线算法。
一、扫描线算法
扫描线算法是一种基于与坐标轴平行的扫描线的图形填充算法。
该算法通过先将所需填充区域划分为多个扫描线,然后沿着每条扫描线对相应像素点进行填充。
扫描线算法的基本流程如下:
1. 将所需填充区域和扫描线分别表示为坐标集合;
2. 对扫描线按照纵坐标进行排序;
3. 从上至下扫描每条扫描线;
4. 遇到新的线段时,将线段入栈;
5. 遇到线段结束时,将该线段出栈,并对当前扫描线区域进行填充。
二、多边形填充算法
多边形填充算法是一种用于对多边形内部进行填充的图形算法。
该算法通过先确定多边形内部的一点,然后通过该点向外扩展直到覆盖整个多边形区域。
目前常用的多边形填充算法包括:边界填充算法、种子填充算法和扫描线填充算法。
三、画线算法
画线算法是一种用于对直线进行绘制的图形算法。
目前常用的画线算法包括:中点画线算法、浮点画线算法和 Bresenham 算法等。
其中,中点画线算法通过将直线划分为许多小区间,然后选择每个区间中距离直线最近的像素点进行绘制;浮点画线算法则主要通过浮点数计算来实现直线的绘制;而 Bresenham 算法则是一种基于光栅化原理的画线算法,性能较高且精度较高。
总之,基本光栅图形算法是计算机图形学中非常重要的一部分,能够帮助我们实现各种各样的图形绘制和填充效果。
在实际应用中,我们可根据需求选择不同的算法来满足具体的绘图需求。
多边形的填充——扫描线算法(原理)2007年10月05日星期五 11:52多边形在计算机中有两种表示:点阵表示和顶点表示。
顶点表示是用多边形的顶点的序列来描述多边形,该表示几何意义强、占内存少,但它不能直观地说明哪些像素在多边形内。
点阵表示是用位于多边形内的象素的集合来刻划多边形,该方法虽然没有多边形的几何信息,但具有面着色所需要的图像表示形式。
多边形填充就是把多边形的顶点表示转换为点阵表示,即从多边形的给定边界出发,求出位于其内部的各个像素,并将帧缓冲器内的各个对应元素设置为相应的灰度或颜色。
多边形填充最常用的方法就是扫描线算法。
下面分两篇文章介绍这种算法的原理和具体实现。
这里所介绍的算法只是针对非自交多边形,这些多边形可以是凸的、凹的或者带有空洞的。
所谓扫描线算法就是找到多边形的最小y值和最大y值,然后用这个范围内的每一条水平线与多边形相交,求得交点,再绘制线段。
所以我们只需要对一条水平线进行分析就可以。
很显然,一条扫描线和多边形有偶数个交点,将这些交点按照x值从小到大排列,然后取第1、2个绘制,第3、4个绘制......直到所有交点都被取完。
所以,对于一条扫描线,我们需要做的工作可以分为三个步骤:1)求出扫描线与多边形边的交点 2)将交点按照x升序排列 3)将排好序的交点两两配对,然后绘制相应线段。
这三个步骤中,后两个步骤很简单,没有特别的内容需要介绍。
但是第一个步骤比较麻烦。
这里有几个问题需要解决。
一是当扫描线与顶点相交时,交点的取舍。
当与那个顶点关联的边在扫描线同侧时,交点自然算两次,当与那个顶点关联的边在扫描线两侧时,交点只能算一次。
我们使用“下闭上开”的办法。
二是多边形边界上的像素取舍,我们采用“左闭右开”的办法。
三是如何减少计算量。
在绘制直线时,有一种DDA算法,它是利用(x,y)直接求出下一个点位于(x+1,y+m)或者(x+1/m, y+1)。
在这里可以利用这一点。
当已经得到y = e和多边形所有边的交点时,对于下一条扫描线y=e+1,如果没有新边与y=e+1相交,就可以推出y = e+1 和多边形所有边的交点。
线生成面的算法在计算机图形学中,线生成面的算法是一种用于将线段转化为面的方法。
通过这种算法,可以将离散的线段连接起来,形成一张平面图像。
本文将介绍几种常用的线生成面算法,并对其原理和应用进行详细解析。
一、扫描线算法扫描线算法是将线段转化为面的常用方法之一。
其基本思想是通过按行扫描的方式,将线段与扫描线的交点进行连接,形成封闭的面。
具体而言,扫描线算法分为以下几个步骤:1. 初始化扫描线位置和线段列表。
2. 按行扫描,记录扫描线与线段的交点。
3. 对于每个交点,根据其位置和线段的属性进行判断,确定所要生成的面的属性。
4. 将生成的面加入到面列表中。
5. 重复以上步骤,直至扫描完整个图像。
扫描线算法的优点是简单易懂,适用于处理简单的图形。
然而,对于复杂的图形,扫描线算法的效率较低,需要较多的计算。
因此,在实际应用中,需要根据具体情况选择合适的算法。
二、边界填充算法边界填充算法是一种将线段转化为面的常用方法。
其基本思想是通过确定面的边界,将边界内的像素点填充为面的颜色。
具体而言,边界填充算法分为以下几个步骤:1. 初始化边界点和填充颜色。
2. 找到边界点的邻域点,判断其是否在边界内。
3. 如果邻域点在边界内,则将其填充为面的颜色。
4. 重复以上步骤,直至填充完整个面。
边界填充算法的优点是适用于处理复杂的图形,可以生成具有多边形形状的面。
然而,边界填充算法可能存在漏填或重复填充的问题,需要进行一定的优化处理。
三、逐点扫描算法逐点扫描算法是一种将线段转化为面的常用方法。
其基本思想是通过对每个像素点进行扫描,判断其是否在线段上,从而生成面。
具体而言,逐点扫描算法分为以下几个步骤:1. 初始化像素点和线段属性。
2. 对于每个像素点,计算其与线段的距离。
3. 判断距离是否小于等于一定阈值,如果是,则将该像素点归为面的一部分。
4. 重复以上步骤,直至扫描完整个图像。
逐点扫描算法的优点是精确度高,可以生成较为细腻的图像。
简述面的两种栅格化算法的实现原理一、引言随着计算机技术的不断发展,图形学也得到了飞速的发展。
在图形学中,栅格化是一个非常重要的概念,它是指将连续的几何图形转换为离散的像素点集合。
在实际应用中,栅格化算法有很多种,其中最常见的就是面的栅格化算法。
本文将详细介绍面的两种栅格化算法的实现原理。
二、扫描线算法1. 算法思想扫描线算法是一种基于扫描线的面栅格化算法。
它的基本思想是:先将多边形按照纵坐标从小到大排序,然后从上往下依次扫描每一条水平线段,找出与该水平线段相交的所有边,并记录下它们相交点所对应的像素点。
2. 算法流程(1)对多边形按照纵坐标从小到大排序。
(2)从上往下依次扫描每一条水平线段。
(3)找出与该水平线段相交的所有边,并记录下它们相交点所对应的像素点。
(4)将记录下来的像素点按照横坐标从小到大排序,并依次填充颜色。
3. 算法优缺点(1)优点:扫描线算法的时间复杂度为O(nlogn),比较高效。
(2)缺点:对于非凸多边形,需要进行分割处理;同时,对于存在重叠部分的多边形,需要进行处理。
三、边界填充算法1. 算法思想边界填充算法是一种基于递归的面栅格化算法。
它的基本思想是:从多边形内部某个像素点开始,向四周扩散填充颜色,并递归地向外扩散。
具体实现时,可以采用四联通或者八联通方式进行扩散。
2. 算法流程(1)从多边形内部某个像素点开始,向四周扩散填充颜色,并递归地向外扩散。
(2)在递归过程中,需要判断当前像素点是否在多边形内部,并且是否已经被填充过颜色。
3. 算法优缺点(1)优点:边界填充算法能够很好地处理非凸多边形和存在重叠部分的多边形。
(2)缺点:由于采用了递归方式,算法的效率比较低,同时也容易出现栈溢出等问题。
四、总结面的栅格化算法是图形学中的重要概念之一。
本文介绍了两种常见的面栅格化算法:扫描线算法和边界填充算法。
扫描线算法通过扫描每一条水平线段来找出多边形内部所有像素点,并进行填充;而边界填充算法则是从一个内部像素点开始,递归地向外扩散填充颜色。