【重磅】初中数学竞赛辅导讲座19讲(全套)

初一数学竞赛讲座第3讲奇偶分析我们知道，全体自然数按被2除的余数不同可以划分为奇数与偶数两大类。

被2除余1的属于一类，被2整除的属于另一类。

前一类中的数叫做奇数，后一类中的数叫做偶数。

关于奇偶数有一些特殊性质，比如，奇数≠偶数，奇数个奇数之和是奇数等。

灵活、巧妙、有意识地利用这些性质，加上正确的分析推理，可以解决许多复杂而有趣的问题。

用奇偶数性质解题的方法称为奇偶分析，善于运用奇偶分析，往往有意想不到的效果。

例1 右表中有15个数，选出5个数，使它们的和等于30，你能做到吗？为什么？分析与解：如果一个一个去找、去试、去算，那就太费事了。

因为无论你选择哪5个数，它们的和总不等于30，而且你还不敢马上断言这是做不到的。

最简单的方法是利用奇偶数的性质来解，因为奇数个奇数之和仍是奇数，表中15个数全是奇数，所以要想从中找出5个使它们的和为偶数，是不可能的。

例2 小华买了一本共有96张练习纸的练习本，并依次将它的各面编号（即由第1面一直编到第192面）。

小丽从该练习本中撕下其中25张纸，并将写在它们上面的50个编号相加。

试问，小丽所加得的和数能否为2000？解：不能。

由于每一张上的两数之和都为奇数，而25个奇数之和为奇数，故不可能为2000。

说明：“相邻两个自然数的和一定是奇数”，这条性质几乎是显然的，但在解题过程中，能有意识地运用它却不容易做到，这要靠同学们多练习、多总结。

例3 有98个孩子，每人胸前有一个号码，号码从1到98各不相同。

试问：能否将这些孩子排成若干排，使每排中都有一个孩子的号码数等于同排中其余孩子号码数的和？并说明理由。

解：不能。

如果可以按要求排成，每排中都有一个孩子的号码数等于同排中其余孩子号码数的和，那么每一排中各号码数之和都是某一个孩子号码数的2倍，是个偶数。

所以这98个号码数的总和是个偶数，但是这98个数的总和为1+2+…+98=99×49，是个奇数，矛盾！所以不能按要求排成。

基础知识1．面积公式由于平面上的凸多边形都可以分割成若干三角形，故在面积公式中最基本的是三角形的面积公式．它形式多样，应在不同场合下选择最佳形式使用．设△ABC ，c b a ,,分别为角C B A ,,的对边，a h 为a 的高，R 、r 分别为△ABC外接圆、内切圆的半径，)(21c b a p ++=．则△ABC 的面积有如下公式：（1）a ABC ah S 21=∆；（2）A bc S ABCsin 21=∆ （3）))()((c p b p a p p S ABC ---=∆（4）pr c b a r S ABC =++=∆)(21（5）Rabc S ABC 4=∆（6）C B A R S ABC sin sin sin 22=∆（7）)sin(2sin sin 2C B CB a S ABC +=∆ （8）)(21a cb r S a ABC -+=∆ （9）)2sin 2sin 2(sin 212C B A R S ABC++=∆ 2．面积定理（1）一个图形的面积等于它的各部分面积这和； （2）两个全等形的面积相等；（3）等底等高的三角形、平行四边形、梯形（梯形等底应理解为两底和相等）的面积相等；（4）等底（或等高）的三角形、平行四边形、梯形的面积的比等于其所对应的高（或底）的比；（5）两个相似三角形的面积的比等于相似比的平方；（6）共边比例定理：若△PAB 和△QAB 的公共边AB 所在直线与直线PQ 交于M ，则QM PM S S Q AB PAB ::=∆∆；（7）共角比例定理：在△ABC 和△C B A '''中，若A A '∠=∠或︒='∠+∠180A A ，则C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆． 3．张角定理：如图，由P 点出发的三条射线PC PB PA ,,，设α=∠APC ，β=∠CPB ，︒<+=∠180βαAPB ，则C B A ,,三点共线的充要条件是：PCPA PB )sin(sin sin βαβα+=+．例题分析例1．梯形ABCD 的对角线BD AC ,相交于O ，且m S AOB =∆，n S COD =∆，求ABCD S 例2．在凸五边形ABCDE 中，设1=====∆∆∆∆∆EAB D EA CD E BCD ABC S S S S S ，求此五边形的面积．例3．G 是△ABC 内一点，连结CG BG AG ,,并延长与AB CA BC ,,分别交于F E D ,,，△AGF 、△BGF 、△BGD 的面积分别为40，30，35，求△ABC 的面积．例4．R Q P ,,分别是△ABC 的边BC AB ,和CA 上的点，且1====RC QR PQ BP ，求△ABC 的面积的最大值．例5．过△ABC 内一点引三边的平行线DE ∥BC ，FG ∥CA ，HI ∥AB ，点I H G F E D ,,,,,都在△ABC 的边上，1S 表示六边形DGHEFI 的面积，2S 表示 △ABC的面积．求证：2132S S ≥．例6．在直角△ABC 中，AD 是斜边BC 上的高，过△ABD 的内心与△ACD 的内心的直线分别交边AB 和AC 于K 和L ，△ABC 和△AKL 的面积分别记为S 和T ．求证：T S 2≥．例7．锐角三角形ABC 中，角A 等分线与三角形的外接圆交于一点1A ，点1B 、1C 与此类似，直线1AA 与B 、C 两角的外角平分线将于一点0A ，点0B 、0C 与此类似．求证：（1）三角形000C B A 的面积是六边形111CB BA AC 的面积的二倍； （2）三角形000C B A 的面积至少是三角形ABC 的四倍．例8．在△ABC 中，R Q P ,,将其周长三等分，且Q P ,在边AB 上，求证：92>∆∆ABCPQR S S ． 例9．在锐角△ABC 的边BC 边上有两点E 、F ，满足CAF BAE ∠=∠，作AB FM ⊥，AC FM ⊥（N M ,是垂足），延长AE 交△ABC 的外接圆于点D ，证明四边形AMDN 与△ABC 的面积相等． 三．面积的等积变换等积变换是处理有关面积问题的重要方法之一，它的特点是利用间面积相等而进行相互转换证（解）题．例10．凸六边形ABCDEF 内接于⊙O ，且13+===DC BC AB ，1===FA EF DE ，求此六边形的面积．例11．已知ABC ∆的三边c b a >>，现在AC 上取AB B A ='，在BA 延长线上截取BC C B ='，在CB 上截取CA A C ='，求证：C B A ABC S S '''∆∆>．例12．C B A '''∆在ABC ∆内，且ABC ∆∽C B A '''∆，求征：ABC AB C CA B BC A S S S S ∆'∆'∆'∆=++ 例13．在ABC ∆的三边AB CA BC ,,上分别取点F E D ,,，使EA CE DC BD 3,3==，FB AF 3=，连CF BE AD ,,相交得三角形PQR ，已知三角形ABC 的面积为13，求三角形PQR 的面积．例14．E 为圆内接四边形ABCD 的AB 边的中点，AD EF ⊥于F ，BC EH ⊥于H ，CD EG ⊥于G ，求证：EF 平分FH ．例15．已知边长为,,,c b a 的ABC ∆，过其内心I 任作一直线分别交AC AB ,于N M ,点，求证：bca IN MI +≤． 例16．正△PQR ≅正△R Q P '''，1a AB =，1b BC =，2a CD =，2b DE =，3a EF =，3b FA =．求证：232221232221b b b a a a ++=++．例17．在正ABC ∆内任取一点O ，设O 点关于三边AB CA BC ,,的对称点分别为C B A ''',,，则C C B B A A ''',,相交于一点P ．例18．已知CE AC ,是正六边形ABCDEF 的两条对角线，点N M ,分别内分ACCE ，且使k CECNAC AM ==，如果N M B ,,三点共线，试求k 的值． 例19．设在凸四边形ABCD 中，直线CD 以AB 为直径的圆相切，求证：当且仅当BC ∥AD 时，直线AB 与以CD 为直径的圆相切．训练题1．设ABC ∆的面积为102cm ，F E D ,,分别是CA BC AB ,,边上的点，且,3,2cm DB cm AD ==若DBEF ABE S S =∆，求ABE ∆的面积．2．过ABC ∆内一点作三条平行于三边的直线，这三条直线将ABC ∆分成六部份，其中，三部份为三角形，其面积为321,,S S S ，求三角形ABC ∆的面积．3．在ABC ∆的三边CA BC AB ,,上分别取不与端点重合的三点L K M ,,，求证：AML ∆，CLK BKM ∆∆,中至少有一个的面积不大于ABC ∆的面积的41．4．锐角ABC ∆的顶角A 的平分线交BC 边于L ，又交三角形的外接圆于N ，过L 作AB 和AC 边的垂线LK 和LM ,垂足是M K ,，求证：四边形AKNM 的面积等于ABC ∆的 面积．5．在等腰直角三角形ABC 的斜边BC 上取一点D ，使BC DC 31=，作ADBE ⊥交AC 于E ，求证：EC AE =．6．三条直线n m l ,,互相平行，n l ,在m 的两侧，且m l ,间的距离为2，n m ,间的距离为1，若正ABC ∆的三个顶点分别在n m l ,,上，求正ABC ∆的边长． 7．已知321P P P ∆及其内任一点P ，直线P P i 分别交对边于i Q （3,2,1=i ），证明：在332211,,PQ P P PQ P P PQ P P 这三个值中，至少有一个不大于2，并且至少有一个不小于2．8．点D 和E 分别在ABC ∆的边AB 和BC 上，点K 和M 将线段DE 分为三等分，直线BK 和BM 分别与边AC 相交于点T 和P ，证明：AC TP 31≤．9．已知P 是ABC ∆内一点，延长CP BP AP ,,分别交对边于C B A ''',,，其中x AP =，w C P B P A P z CP y BP ='='='==,,，且3,23==++w z y x ，求xyz 之值． 10．过点P 作四条射线与直线l l ',分别交于D C B A ,,,和D C B A '''',,,，求证：CB D A DC B A BC AD CD AB ''⋅''''⋅''=⋅⋅． 11．四边形ABCD 的两对对边的延长线分别交L K ,，过L K ,作直线与对角线BD AC ,的延长线分别F G ,，求证：KGLGKFLF=． 12．G 为ABC ∆的重心，过G 作直线交AC AB ,于F E ,，求证：GF EG 2≤．同余式与不定方程同余式和不定方程是数论中古老而富有魅力的内容.考虑数学竞赛的需要,下面介绍有关的基本内容.1. 同余式及其应用定义:设a、b、m为整数（m＞0），若a和b被m除得的余数相同，则称a和b对模m同余.记为或一切整数n可以按照某个自然数m作为除数的余数进行分类，即n=pm+r （r=0，1，…，m-1），恰好m个数类.于是同余的概念可理解为,若对n1、n2，有n1=q1m+r，n2=q2m+r，那么n1、n2对模m的同余，即它们用m除所得的余数相等.利用整数的剩余类表示,可以证明同余式的下述简单性质:(1) 若,则m|(b-a).反过来,若m|(b-a),则;(2) 如果a=km+b(k为整数),则;(3) 每个整数恰与0,1,…，m-1，这m个整数中的某一个对模m 同余；(4) 同余关系是一种等价关系：①反身性；②对称性，则，反之亦然.③传递性，，则；（5）如果，，则①；②特别地应用同余式的上述性质，可以解决许多有关整数的问题.例1（1898年匈牙利奥林匹克竞赛题）求使2n+1能被3整除的一切自然数n.解∵∴则2n+1∴当n为奇数时，2n+1能被3整除；当n为偶数时，2n+1不能被3整除.例2 求2999最后两位数码.解考虑用100除2999所得的余数.∵∴又∴∴∴2999的最后两位数字为88.例3 求证31980+41981能被5整除.证明∵∴∴∴2．不定方程不定方程的问题主要有两大类：判断不定方程有无整数解或解的个数；如果不定方程有整数解，采取正确的方法，求出全部整数解.(1) 不定方程解的判定如果方程的两端对同一个模m(常数)不同余,显然,这个方程必无整数解.而方程如有解则解必为奇数、偶数两种，因而可以在奇偶性分析的基础上应用同余概念判定方程有无整数解.例4 证明方程2x2-5y2=7无整数解.证明∵2x2=5y2+7，显然y为奇数.①若x为偶数，则∴∵方程两边对同一整数8的余数不等，∴x不能为偶数.②若x为奇数，则但5y2+7∴x不能为奇数.因则原方程无整数解.说明:用整数的整除性来判定方程有无整数解,是我们解答这类问题的常用方法.例5 (第14届美国数学邀请赛题)不存在整数x,y使方程①证明如果有整数x，y使方程①成立，则=知（2x+3y2）+5能被17整除.设2x+3y=17n+a，其中a是0，±1，±2，±3，±4，±5，±6，±7，±8中的某个数，但是这时（2x+3y）2+5=（17n）2+34na+（a2+5）=a2+5（mod17），而a2+5被17整除得的余数分别是5，6，9，14，4，13，7，3，1，即在任何情况下（2x+3y）2+5都不能被17整除，这与它能被17整除矛盾.故不存在整数x，y使①成立.例7 （第33届美国数学竞赛题）满足方程x2+y2=x3的正整数对（x，y）的个数是（）.（A）0 （B）1（C）2（D）无限个（E）上述结论都不对解由x2+y2=x3得y2=x2（x-1），所以只要x-1为自然数的平方，则方程必有正整数解.令x-1=k2(k为自然数),则为方程的一组通解.由于自然数有无限多个,故满足方程的正整数对(x,y)有无限多个,应选(D).说明:可用写出方程的一组通解的方法,判定方程有无数个解.(2) 不定方程的解法不定方程没有统一的解法,常用的特殊方法有:配方法、因式（质因数）分解法、不等式法、奇偶分析法和余数分析法.对方程进行适当的变形,并正确应用整数的性质是解不定方程的基本思路.例6 求方程的整数解.解(配方法)原方程配方得(x-2y)2+y2=132.在勾股数中,最大的一个为13的只有一组即5,12,13,因此有8对整数的平方和等于132即(5,12),(12,5),(-5,-12),(-12,-5),(5-,12),(12,-5),(-5,12),(-12,5).故原方程组的解只能是下面的八个方程组的解解得例7 (原民主德国1982年中学生竞赛题)已知两个自然数b和c及素数a满足方程a2+b2=c2.证明:这时有a＜b及b+1=c.证明（因式分解法）∵a2+b2=c2，∴a2=（c-b）（c+b），又∵a为素数，∴c-b=1，且c+b=a2.于是得c=b+1及a2=b+c=2b+1＜3b，即＜.而a≣3,∴≢1，∴＜1.∴a＜b.例9（第35届美国中学数学竞赛题）满足联立方程的正整数（a，b，c）的组数是（）.（A）0 （B）1 （C）2 （D）3 （E）4解（质因数分解法）由方程ac+bc=23得（a+b）c=23=1³23.∵a，b，c为正整数，∴c=1且a+b=23.将c和a=23-b代入方程ab+bc=44得(23-b)b+b=44,即(b-2)(b-22)=0,∴b1=2,b2=22.从而得a1=21,a2=1.故满足联立方程的正整数组(a,b,c)有两个,即(21,2,1)和(1,22,1),应选(C).例10求不定方程2(x+y)=xy+7的整数解.解由(y-2)x=2y-7,得分离整数部分得由x为整数知y-2是3的因数,∴y-2=±1，±3，∴x=3，5，±1.∴方程整数解为例11 求方程x+y=x2-xy+y2的整数解.解（不等式法）方程有整数解必须△=（y+1）2-4（y2-y）≣0，解得≢y≢.满足这个不等式的整数只有y=0，1，2.当y=0时，由原方程可得x=0或x=1；当y=1时，由原方程可得x=2或0；当y=2时，由原方程可得x=1或2.所以方程有整数解最后我们来看两个分式和根式不定方程的例子.例12 求满足方程且使y是最大的正整数解（x，y）.解将原方程变形得由此式可知，只有12-x是正的且最小时，y才能取大值.又12-x应是144的约数，所以，12-x=1，x=11，这时y=132.故满足题设的方程的正整数解为（x，y）=（11，132）.例13（第35届美国中学生数学竞赛题）满足0＜x＜y及的不同的整数对（x，y）的个数是（）.（A）0 （B）1 （C）3 （D）4 （E）7解法1 根据题意知，0＜x＜1984，由得当且仅当1984x是完全平方数时，y是整数.而1984=26²31，故当且仅当x具有31t2形式时，1984x是完全平方数.∵x＜1984，∵1≢t≢7.当t=1，2，3时，得整数对分别为（31，1519）、（124，1116）和（279，775）.当t＞3时y≢x不合题意，因此不同的整数对的个数是3，故应选（C）.解法2 ∵1984=∴由此可知：x必须具有31t2形式，y 必须具有31k2形式，并且t+k=8（t，k均为正整数）.因为0＜x＜y，所以t＜k.当t=1，k=7时得（31，1519）；t=2，k=6时得（124，1116）；当t=3，k=5时得（279，775）.因此不同整数对的个数为3.练习二十1. 选择题(1)方程x2-y2=105的正整数解有( ).（A）一组（B）二组（C）三组（D）四组(2)在0,1,2,…，50这51个整数中，能同时被2，3，4整除的有（）.（A） 3个（B）4个（C）5个（D）6个2．填空题（1）的个位数分别为_________及_________.(2)满足不等式104≢A≢105的整数A的个数是x³104+1，则x的值________.(3) 已知整数y被7除余数为5,那么y3被7除时余数为________.(4) (全俄第14届中学生数学竞赛试题)求出任何一组满足方程x2-51y2=1的自然数解x和y_________.3.(第26届国际数学竞赛预选题)求三个正整数x、y、z满足.4．（1985年上海数学竞赛题）在数列4，8，17，77，97，106，125，238中相邻若干个数之和是3的倍数，而不是9的倍数的数组共有多少组？5．求的整数解.6．求证可被37整除.7．（全俄1986年数学竞赛题）求满足条件的整数x，y的所有可能的值.8．（1985年上海初中数学竞赛题）已知直角三角形的两直角边长分别为l厘米、m厘米，斜边长为n厘米，且l，m，n均为正整数，l为质数.证明：2（l+m+n）是完全平方数.9.(1988年全国初中数学竞赛题)如果p、q、、都是整数，并且p＞1，q＞1，试求p+q的值.练习二十1.D.C.2.(1)9及1. (2)9. (3)4.(4)原方程可变形为x2=(7y+1)2+2y(y-7),令y=7可得x=50.3.不妨设x≢y≢z,则,故x≢3.又有故x≣2.若x=2,则,故y≢6.又有,故y≣4.若y=4,则z=20.若y=5,则z=10.若y=6,则z无整数解.若x=3,类似可以确定3≢y≢4,y=3或4,z 都不能是整数.4.可仿例2解.5.先求出,然后将方程变形为y=5+x-2要使y为整数,5x-1应是完全平方数,…,解得6.8888≡8(mod37),∴88882222≡82(mod37).7777≡7(mod37),77773333≡73(mod37),88882222+77773333≡(82+73)(mod37),而82+73=407,37|407,∴37|N.7.简解:原方程变形为3x2-(3y+7)x+3y2-7y=0由关于x的二次方程有解的条件△≣0及y为整数可得0≢y≢5,即y=0,1,2,3,4,5.逐一代入原方程可知,原方程仅有两组解(4,5)、(5,4).8.∵l2+m2=n2,∴l2=(n+m)(n-m).∵l为质数,且n+m＞n-m＞0,∴n+m=l2,n-m=1.于是l2=n+m=(m+1)+m=2m+1,2m=l2-1,2(l+m+1)=2l+2+2m=l2+2l+1=(l+1)2.即2(l+m+1)是完全平方数.9.易知p≠q,不妨设p＞q.令=n,则m＞n由此可得不定方程(4-mn)p=m+2,解此方程可得p、q之值.几何解题途径的探求方法一．充分地展开想象想象力，就是人们平常说的形象思维或直觉思维能力。

第十九讲* 平面几何中的几个著名定理几何学起源于土地测量，几千年来，人们对几何学进行了深入的研究，现已发展成为一门具有严密的逻辑体系的数学分支．人们从少量的公理出发，经过演绎推理得到不少结论，这些结论一般就称为定理．平面几何中有不少定理，除了教科书中所阐述的一些定理外，还有许多著名的定理，以这些定理为基础，可以推出不少几何事实，得到完美的结论，以至巧妙而简捷地解决不少问题．而这些定理的证明本身，给我们许多有价值的数学思想方法，对开阔眼界、活跃思维都颇为有益．有些定理的证明方法及其引伸出的结论体现了数学的美，使人们感到对这些定理的理解也可以看作是一种享受．下面我们来介绍一些著名的定理．1．梅内劳斯定理亚历山大里亚的梅内劳斯(Menelaus，约公元100年，他和斯巴达的Menelaus是两个人)曾著《球面论》，着重讨论球面三角形的几何性质．以他的名子命名的“梅内劳斯定理”现载在初等几何和射影几何的书中，是证明点共线的重要定理．定理一直线与△ABC的三边AB，BC，CA或延长线分别相交于X，Y，Z，则证过A，B，C分别作直线XZY的垂线，设垂足分别为Q，P，S，见图3－98．由△AXQ∽△BXP得同理将这三式相乘，得说明 (1)如果直线与△ABC的边都不相交，而相交在延长线上，同样可证得上述结论，但一定要有交点，且交点不在顶点上，否则定理的结论中的分母出现零，分子也出现零，这时定理的结论应改为AX×BY×CZ=XB×YC×ZA，仍然成立．(2)梅内劳斯定理的逆定理也成立，即“在△ABC的边AB和AC上分别取点X，Z，在BC的延长线上取点Y，如果那么X，Y，Z共线”．梅内劳斯定理的逆定理常被用来证明三点共线．例1 已知△ABC的内角∠B和∠C的平分线分别为BE和CF，∠A的外角平分线与BC的延长线相交于D，求证：D，E，F共线．证如图3－99有相乘后得由梅内劳斯定理的逆定理得F，D，E共线．例2(戴沙格定理)在△ABC和△A′B′C′中，若AA′，BB′，CC′相交于一点S，则AB与A′B′，BC与B′C′，AC与A′C′的交点F，D，E共线．证如图3－100，直线FA′B′截△SAB，由梅内劳斯定理有同理，直线EC′A′和DC′B′分别截△SAC和△SBC，得将这三式相乘得所以D，E，F共线．2．塞瓦定理意大利数学家塞瓦(G．Ceva)在1678年发表了下面的十分有用的定理，它是证明共点线的重要定理．定理在△ABC内任取一点P，直线AP，BP，CP分别与边BC，CA，AB 相交于D，E，F，则证如图3－101，过B，C分别作直线AP的垂线，设垂足为H和K，则由于△BHD∽△CKD，所以同理可证将这三式相乘得说明 (1)如果P点在△ABC外，同样可证得上述结论，但P点不能在直线AB，BC，CA上，否则，定理的结论中的分母出现零，分子也出现零，这时，定理的结论应改为BD×CE×AF=DC×EA×FB，仍然成立．(2)塞瓦定理的逆定理也成立，即“在△ABC的边BC，CA，AB上分别取点D，E，F，如果那么直线AD，BE，CF相交于同一点．”证如图3－102，设AD和BE相交于P，作直线CP，交直线AB于F′，由塞瓦定理得所以 F′B=FB，即F′与F重合，所以AD，BE，CF相交于同一点．塞瓦定理的逆定理常被用来证明三线共点．例3 求证：三角形的三条中线、三条内角平分线和三条高所在的直线分别相交于同一点．证 (1)如果D，E，F分别是△ABC的边BC，CA，AB的中点，则由塞瓦定理的逆定理得中线AD，BE，CF共点．(2)如果D，E，F分别是△ABC的内角平分线AD，BE，CF与边BC，CA，AB的交点，则由塞瓦定理的逆定理得角平分线AD，BE，CF共点．(3)设D，E，F分别是△ABC的高AD，BE，CF的垂足．(i)当△ABC是锐角三角形时(如图3－103)，D，E，F分别在BC，CA，AB上，有BD=ccosB，DC=bcosC，CE=acosc，EA=ccosA，AF=bcosA，FB=acosB，所以由塞瓦定理的逆定理得高AD，BE，CF共点．(ii)当△ABC是钝角三角形时，有BD=ccosB，DC=bcosC，CE=acosC，EA=ccos(180°-A)=-ccosA，AF=bcos(180°-A)=-bcosA,FB=acosB，所以由塞瓦定理的逆定理，得高AD，BE，CF共点．(iii)当△ABC是直角三角形时，高AD，BE，CF都经过直角顶点，所以它们共点．例4 在三角形ABC的边上向外作正方形，A1，B1，C1是正方形的边BC，CA，AB的对边的中点，证明：直线AA1，BB1，CC1相交于一点．证如图3－104．设直线AA1，BB1，CC1与边BC，CA，AB的交点分别为A2，B2，C2，那么BA2：A2C等于从点B和C到边AA1的垂线的长度之比，即其中∠θ=∠CBA1=∠BCA1．同理将上述三式相乘得根据塞瓦定理的逆定理，得AA1，BB1，CC1共点．3．斯台沃特定理定理△ABC的边BC上任取一点D，若BD=u，DC=v，AD=t，则证过A作AE⊥BC，E为垂足(如图3－105)，设DE=x，则有AE2=b2-(v-x)2=c2-(u+x)2=t2-x2，(若E在BC的延长线上，则v-x换成x-v．)于是得消去x得(u+v)2=b2u+c2v-uv(u+v)，这就是中线长公式．(2)当AD是△ABC的内角平分线时，由三角形的内角平分线的性质设a+b+c=2p，得这就是内角平分线长公式．(3)当AD是△ABC的高时，AD2=b2-u2=c2-v2．再由u+v=a，解得所以若设AD=h a，则这就是三角形的高线长公式．当D在BC的延长线上时，用-v代替v，同样可得高线长线公式．这就是三角形的面积公式．伦公式例5 如图3－106．在△ABC中，c＞b，AD是△ABC的角平分线，E 在BC上，BE=CD．求证：AE2-AD2=(c-b)2．证为方便起见，设BD=u，DC=v，则BE=v，EC=u．由斯台沃特定理得所以因为AD是角平分线，所以于是4．托勒密定理托勒密(Ptolemy，约公元85～165年)是古代天文学的集大成者．一般几何教科书中的“托勒密定理”(圆内接四边形的对边积之和等于对角线之积)，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。

初中数学竞赛辅导资料第一讲 数的整除一、内容提要：如果整数A 除以整数B(B ≠0)所得的商A/B 是整数,那么叫做A 被B 整除。

0能被所有非零的整数整除.能被7整除的数的特征：①抹去个位数 ②减去原个位数的2倍 ③其差能被7整除.如 1001 100－2＝98（能被7整除）又如7007 700－14＝686, 68－12＝56（能被7整除） 能被11整除的数的特征：①抹去个位数 ②减去原个位数 ③其差能被11整除 如 1001 100－1＝99(能11整除）又如10285 1028－5＝1023 102－3＝99（能11整除） 二、例题例1已知两个三位数328和92x 的和仍是三位数75y 且能被9整除。

求x,y解:x ，y 都是0到9的整数，∵75y 能被9整除，∴y=6。

∵328＋92x ＝567，∴x=3 例2已知五位数x 1234能被12整除，求x解：∵五位数能被12整除，必然同时能被3和4整除， 当1＋2＋3＋4＋x 能被3整除时，x=2，5，8 当末两位4x 能被4整除时，x ＝0，4，8∴x ＝8例3求能被11整除且各位字都不相同的最小五位数解：五位数字都不相同的最小五位数是10234，但（1＋2＋4)－（0＋3）＝4，不能被11整除，只调整末位数仍不行 调整末两位数为30，41，52，63，均可，∴五位数字都不相同的最小五位数是10263.练习一1、分解质因数：(写成质因数为底的幂的连乘积）①756②1859③1287④3276⑤10101⑥10296987能被3整除，那么a=_______________2、若四位数ax能被11整除，那么x＝__________3、若五位数123435m能被25整除4、当m=_________时，59610能被7整除5、当n=__________时，n6、能被11整除的最小五位数是________，最大五位数是_________7、能被4整除的最大四位数是____________，能被8整除的最大四位数是_________。

初一数学竞赛讲义重难点有效突破知识点梳理及重点题型举一反三练习专题01 质数那些事阅读与思考一个大于1的自然数如果只能被1和本身整除，就叫作质数(也叫素数)；如果能被1和本身以外的自然数整除，就叫作合数；自然数1既不是质数，也不是合数，叫作单位数．这样，我们可以按约数个数将正整数分为三类：关于质数、合数有下列重要性质：1．质数有无穷多个，最小的质数是2，但不存在最大的质数，最小的合数是4．2．1既不是质数，也不是合数；2是唯一的偶质数．3．若质数|，则必有|或|．4．算术基本定理：任意一个大于1的整数N能唯一地分解成个质因数的乘积(不考虑质因数之间的顺序关系)：N=，其中，为质数，为非负数(=1，2，3，…，)．正整数N的正约数的个数为(1＋)(1＋)…(1＋)，所有正约数的和为(1＋＋…＋)(1＋＋…＋)…(1＋＋…＋)．例题与求解【例1】已知三个质数，，满足＋＋＋=99，那么的值等于_________________．(江苏省竞赛试题) 解题思想：运用质数性质，结合奇偶性分析，推出，，的值．【例2】若为质数，＋5仍为质数，则＋7为( )A．质数B．可为质数，也可为合数C．合数D．既不是质数，也不是合数(湖北省黄冈市竞赛试题) 解题思想：从简单情形入手，实验、归纳与猜想．【例3】求这样的质数，当它加上10和14时，仍为质数．(上海市竞赛试题) 解题思想：由于质数的分布不规则，不妨从最小的质数开始进行实验，另外，需考虑这样的质数是否唯一，按剩余类加以深入讨论．【例4】⑴将1，2，…，2 004这2 004个数随意排成一行，得到一个数，求证：一定是合数．⑵若是大于2的正整数，求证：－1与＋1中至多有一个质数．⑶求360的所有正约数的倒数和．(江苏省竞赛试题) 解题思想：⑴将1到2 004随意排成一行，由于中间的数很多，不可能一一排出，不妨找出无论怎样排，所得数都有非1和本身的约数；⑵只需说明－1与＋1中必有一个是合数，不能同为质数即可；⑶逐个求解正约数太麻烦，考虑整体求解．【例5】设和是正整数，≠，是奇质数，并且，求＋的值．解题思想：由题意变形得出整除或，不妨设．由质数的定义得到2－1=1或2－1=．由≠及2－1为质数即可得出结论．【例6】若一个质数的各位数码经任意排列后仍然是质数，则称它是一个“绝对质数”[如2，3，5，7，11，13(31)，17(71)，37(73)，79(97)，113(131，311)，199(919，991)，337(373，733)，…都是质数]．求证：绝对质数的各位数码不能同时出现数码1，3，7，9．(青少年国际城市邀请赛试题) 解题思想：一个绝对质数如果同时含有数字1，3，7，9，则在这个质数的十进制表示中，不可能含有数字0，2，4，5，6，8，否则，进行适当排列后，这个数能被2或5整除．能力训练A级1．若，，，为整数，=1997，则=________．2．在1，2，3，…，这个自然数中，已知共有个质数，个合数，个奇数，个偶数，则(－)＋(－)=__________．3．设，为自然数，满足1176=，则的最小值为__________．(“希望杯”邀请赛试题) 4．已知是质数，并且＋3也是质数，则－48的值为____________．(北京市竞赛试题) 5．任意调换12345各数位上数字的位置，所得的五位数中质数的个数是( )A．4B．8C．12D．06．在2 005，2 007，2 009这三个数中，质数有( )A．0个B．1个C．2个D．3个(“希望杯”邀请赛试题) 7．一个两位数的个位数字和十位数字变换位置后，所得的数比原来的数大9，这样的两位中，质数有()A．1个B．3 个C．5个D．6 个(“希望杯”邀请赛试题) 8．设，，都是质数，并且＋=，<．求．9．写出十个连续的自然数，使得个个都是合数．(上海市竞赛试题)10．在黑板上写出下面的数2，3，4，…，1 994，甲先擦去其中的一个数，然后乙再擦去一个数，如此轮流下去，若最后剩下的两个数互质，则甲胜；若最后剩下的两个数不互质，则乙胜，你如果想胜，应当选甲还是选乙？说明理由．(五城市联赛试题)11．用正方形的地砖不重叠、无缝隙地铺满一块地，选用边长为cm规格的地砖，恰用块，若选用边长为cm规格的地砖，则要比前一种刚好多用124块，已知，，都是正整数，且(，)=1，试问这块地有多少平方米？(湖北省荆州市竞赛试题)B级1．若质数，满足5＋7=129，则＋的值为__________．2．已知，均为质数，并且存在两个正整数，，使得=＋，=×，则的值为__________．3．自然数，，，，都大于1，其乘积=2 000，则其和＋＋＋＋的最大值为__________，最小值为____________．(“五羊杯”竞赛试题) 4．机器人对自然数从1开始由小到大按如下的规则染色：凡能表示为两个合数之和的自然数都染成红色，不合上述要求的自然数都染成黄色，若被染成红色的数由小到大数下去，则第1 992个数是_______________．(北京市“迎春杯”竞赛试题) 5．若，均为质数，且满足＋=2 089，则49－=_________．A．0B．2 007C．2 008D．2 010(“五羊杯”竞赛试题) 6．设为质数，并且7＋8和8＋7也都为质数，记=77＋8，=88＋7，则在以下情形中，必定成立的是()A．，都是质数B．，都是合数C．，一个是质数，一个是合数 D．对不同的，以上皆可能出现(江西省竞赛试题) 7．设，，，是自然数，并且，求证：＋＋＋一定是合数．(北京市竞赛试题)8．请同时取六个互异的自然数，使它们同时满足：⑴6个数中任意两个都互质；⑵6个数任取2个，3个，4个，5个，6个数之和都是合数，并简述选择的数符合条件的理由．9．已知正整数，都是质数，并且7＋与＋11也都是质数，试求的值．(湖北省荆州市竞赛试题)10. 41名运动员所穿运动衣号码是1，2，…，40，41这41个自然数，问：(l) 能否使这41名运动员站成一排，使得任意两个相邻运动员的号码之和是质数？(2) 能否让这41名运动员站成一圈，使得任意两个相邻运动员的号码之和都是质数？若能办到，请举出一例；若不能办到，请说明理由．专题01 质数那些事例1 34例2 C例3 3符合要求提示：当p=3k＋1时，p＋10=3k＋11，p＋14=3(k＋5)，显然p＋14是合数，当p=3k＋2时，p＋10=3(k＋4)是合数，当p=3k时，只有k=1才符合题意．例4 （1）因1＋2＋…＋2004=×2004×（1＋2004）=1002×2005为3的倍数，故无论怎样交换这2004个数的顺序，所得数都有3这个约数．（2）因n是大于2的正整数，则－1≥7，－1、、＋1是不小于7的三个连续的正整数，其中必有一个被3整除，但3不整除，故－1与＋1中至多有一个数是质数．（3）设正整数a的所有正约数之和为b，，，，…，为a的正约数从小到大的排列，于是=1，=a．由于中各分数分母的最小公倍数=a，故S===，而a=360=，故b=（1＋2＋＋）×（1＋3＋）×（1＋5）=1170．==．例5 由=，得x＋y==k．（k为正整数），可得2xy=kp，所以p整除2xy且p为奇质数，故p整除x或y，不放设x=tp，则tp＋y=2ty，得y=为整数．又t与2t－1互质，故2t－1整除p，p为质数，所以2t－1=1或2t－1=p．若2t－1=，得t=1，x=y=p，与x≠y矛盾；若2t－1=p，则=，2xy=p（x＋y）．∵p是奇质数，则x ＋y为偶数，x、y同奇偶性，只能同为xy=必有某数含因数p．令x=ap，ay=，2ay=ap＋y．∴y=，故a，2a－1互质，2a－1整除p，又p是质数，则2a－1=p，a=，故x==，∴x＋y=＋=。

第一篇 一元一次方程的讨论第一部分 基本方法1. 方程的解的定义：能使方程左右两边的值相等的未知数的值叫做方程的解。

一元方程的解也叫做根。

例如：方程 2x ＋6＝0， x （x －1）=0, |x |=6, 0x =0, 0x =2的解 分别是： x =－3, x =0或x =1, x =±6, 所有的数，无解。

2. 关于x 的一元一次方程的解（根）的情况：化为最简方程ax =b 后， 讨论它的解：当a ≠0时，有唯一的解 x =ab； 当a =0且b ≠0时，无解；当a =0且b ＝0时，有无数多解。

（∵不论x 取什么值，0x ＝0都成立） 3. 求方程ax =b (a ≠0)的整数解、正整数解、正数解 当a ｜b 时，方程有整数解；当a ｜b ，且a 、b 同号时，方程有正整数解； 当a 、b 同号时，方程的解是正数。

综上所述，讨论一元一次方程的解，一般应先化为最简方程ax =b 第二部分 典例精析例1 a 取什么值时，方程a (a －2)x =4(a －2) ①有唯一的解？②无解？ ③有无数多解？④是正数解？例2 k取什么整数值时，方程①k(x+1)=k－2（x－2）的解是整数？②（1－x）k=6的解是负整数？例3己知方程a(x－2)=b(x+1)－2a无解。

问a和b应满足什么关系？例4a、b取什么值时，方程（3x－2）a+（2x－3）b=8x－7有无数多解？第三部分典题精练1. 根据方程的解的定义，写出下列方程的解：①(x+1)=0, ②x2=9, ③|x|=9，④|x|=－3,⑤3x +1=3x －1, ⑥x +2=2+x2. 关于x 的方程ax =x +2无解，那么a __________3. 在方程a (a －3)x =a 中，当a 取值为＿＿＿＿时，有唯一的解； 当a ＿＿＿时无解；当a ＿＿＿＿＿时,有无数多解； 当a ＿＿＿＿时,解是负数。

4. k 取什么整数值时，下列等式中的x 是整数？① x =k4②x =16-k ③x =k k 32+ ④x =123+-k k5. k 取什么值时，方程x －k =6x 的解是 ①正数？ ②是非负数？6. m 取什么值时，方程3（m +x ）=2m －1的解 ①是零？ ②是正数？7. 己知方程221463+=+-a x 的根是正数，那么a 、b 应满足什么关系？8. m 取什么整数值时，方程m m x 321)13(-=-的解是整数?9. 己知方程ax x b 231)1(2=++有无数多解，求a 、b 的值。

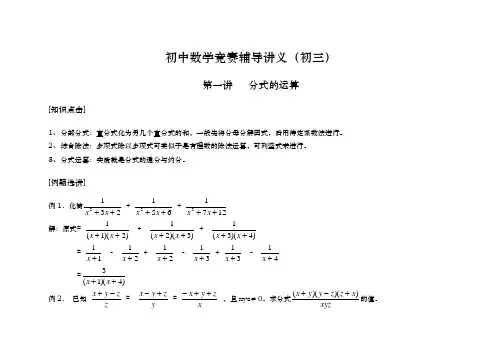
初中数学竞赛辅导讲义（初三）第一讲 分式的运算[知识点击]1、 分部分式：真分式化为另几个真分式的和，一般先将分母分解因式，后用待定系数法进行。

2、 综合除法：多项式除以多项式可类似于是有理数的除法运算，可列竖式来进行。

3、 分式运算：实质就是分式的通分与约分。

[例题选讲]例1．化简2312++x x + 6512++x x + 12712++x x 解：原式= )2)(1(1++x x + )3)(2(1++x x + )4)(3(1++x x = 11+x - 21+x + 21+x - 31+x + 31+x - 41+x =)4)(1(3++x x 例2． 已知 z z y x -+ = y z y x +- = x z y x ++- ，且xyz ≠0，求分式xyz x z z y y x ))()((+-+的值。

解：易知：z y x + = y z x + = x z y + =ｋ 则⎪⎩⎪⎨⎧=+=+=+)3()2()1(kx z y ky z x kz y x （1）+（2）+（3）得：(ｋ-2)(x+y+z)=0 ｋ=2 或 x+y+z=0 若ｋ=2则原式= k 3 = 8 若 ｘ+ｙ+ｚ=0，则原式= k 3 =-1例3．设 12+-mx x x =1，求 12242+-x m x x 的值。

解：显然X 0≠，由已知x mx x 12+- =1 ，则 x +x 1 = ｍ + 1 ∴ 22241x x m x +- = ｘ2 + 21x - ｍ2= (x +x1)2-2 –ｍ2 =( ｍ +1)2-2- ｍ2= 2ｍ -1 ∴原式=121-m 例4．已知多项式3x 3 +ax 2 +3x +1 能被x 2+1整除，求ａ的值。

解：13313232+++++x ax x X ax1- ａ=0 ∴ ａ=1例5：设ｎ为正整数，求证311⨯ + 511⨯ + …… +)12)(12(1+-n n ＜ 21 证：左边=21（1 - 31 + 31 - 51 + …… + 121-n - 121+n ） aaax ax xO x -++++1133223=21（1- 121+n ） ∵n 为正整数，∴121+n ＜ 1 ∴1- 121+n ＜ 1 故左边＜ 21[小结归纳]1、部分分式的通用公式：)(1k x x + = k 1 （x 1 - kx +1） 2、参数法是解决比例问题特别是连比问题时非常有效的方法，其优点在于设连比值为K ，将连等式化为若干个等式，把各字母用同一字母的解析式表示，从而给解题带来方便。

第19讲三角形的“四心”有一个人开始跟欧几里德学习几何学，当他学完第一个命题时，他就问欧几里德：我能通过学习这些东西得到什么好处呢？于是欧几里德叫来他的仆人，并说：给他三个便士，因为他想从所学的知识中获取实利。

——斯托比亚斯知识方法扫描1．三角形的三条角平分线交于一点，这点是三角形的内切圆的圆心，称为三角形的内心。

如果△ABC的内心为I，则有①I 到△ABC的三边距离相等；1∠C；②∠AIB＝90°＋2③若延长CI交三角形ABC的外接圆于D，则DA=DB=DI。

2．三角形的三边的垂直平分线交于一点，这点是三角形的外接圆的圆心，称为三角形的外心。

如果△ABC的外心为O，则有①O到三个顶点的距离相等；②∠AOB＝2∠C；③外心到一边的距离等于这边所对的顶点到垂心的距离的一半。

3．三角形的三条中线交于一点，这点称为三角形的重心。

如果△ABC的重心为G，则有①重心到一个顶点的距离是到对边中点距离的2倍；②△ABG，△BCG，△CAG的面积相等。

4．三角形的三条高所在的直线交于一点，这点称为三角形的垂心。

如果△ABC的垂心为H ，则有①若△ABC是锐角三角形，则∠AHB＝180°－∠C；②若AD是△ABC的高，AD交三角形ABC的外接圆于E，则DE=DH。

经典例题解析例1（1995年全国初中数学联赛试题）如图, 已知∠ACE＝∠CDE＝90°, 点B在CE上, CA＝CB＝CD, 过A、C、D三点的圆交AB于F. 求证：F为△CDE 的内心.分析若连结DF、CF, 显然要证明DF平分∠CDE,CF平分∠DCE. 证明DF平分∠CDE只要证∠CDF＝45°,这是容易解决的. 证明CF平分∠DCE可以转证∠CFD＝∠CFB, 这样便于与已知条件CA＝CD沟通起来.证明∵∠ACE＝90°, CA＝CB, ∴∠A＝45°.连结DF, 则∠CDF＝∠A＝45°.∵∠CDE＝90°, ∴DF平分∠CDE.连结AD、CF. ∵CA＝CD, ∴∠CAD＝∠CDA.∵∠CFD 与∠CAD 互补, ∠CFB 与∠CFA 互补,而∠CFA ＝∠CDA, ∴∠CFB 与∠CDA 互补.∴∠CFD ＝∠CFB. ∴F 是△CDE 的内心.例2 (河南省第三届初中数学竞赛试题) 一条直线DE 平分△ABC 的周长, 同时直线DE 又平分了△ABC 的面积. 求证：直线DE 经过△ABC 的内切圆圆心O.证明 如图, 设点D 、E 分别在边AB 、AC 上, r 为△ABC 的内切圆半径, 连结AO 、BO 、CO 、DO 、EO, 由题设, 得：AD ＋AE ＝BD ＋BC ＋CE,∵r ＞0, ∴2r (AD ＋AE)＝2r (BD ＋BC ＋CE).结合图形, 得：S △AOD ＋S △AOE ＝S △DOB ＋S △BOC ＋S △COE ①又∵DE 平分△ABC 的面积, 由图可知S △ADE ＝S 四边形BCED ②比较①、②, 可知只有当S △DOE ＝0时, 才能使两个等式都成立.，所以直线DE 经过△ABC 的内切圆圆心O.从而O 点必在DE 上, 即直线DE 经过△ABC 的内切圆圆心.例3（2001年我爱数学初中生夏令试题）在锐角△ABC 中，AD ⊥BC ，D 为垂足；DE ⊥AC ，E 为垂足；DF ⊥AB ，F 为垂足，O 为△ABC 的外心，求证：（1）△ABC ∽△AEF ；（2）AO ⊥EF 。

竞赛讲座(有理数的有关知识)一、 知识要点 1、绝对值x 的绝对值x 的意义如下：x =⎩⎨⎧<-≥0x x x x ，如果，如果x 是一个非负数，当且仅当x=0时，x =0绝对值的几何意义是：一个数的绝对值表示这个数对应的数轴上的点到原点的距离；由此可得：b a -表示数轴上a 点到b 点的距离。

2、倒数1除以一个数(零除外)的商，叫做这个数的倒数。

如果两个数互为倒数，那么这两个数的积等于1。

3、相反数绝对值相同而符号相反的两个数互为相反数。

两个互为相反数的数的和等于0。

二、 例题精讲 例1 化简 6312-+--+x x x分析：由2x+1=0、x-3=0、x-6=0求出零点，然后用零点分段法将绝对值去掉，从而达到化简的目的。

解：由2x+1=0、x-3=0、x-6=0 分别求得：x= -1/2， x=3， x=6 当21-<x 时，原式= -(2x+1)+(x-3) - (x-6)= -2x+2 当321<≤-x 时，原式= (2x+1)+(x-3) - (x-6)= 2x+4 当63<≤x 时，原式= (2x+1)-(x-3) - (x-6)= 10当x ≥6时，原式= (2x+1)-(x-3) + (x-6)= 2x-2∴原式=⎪⎪⎩⎪⎪⎨⎧≥<≤<≤-+-<+-时当，时当，时当，时当，6x 2-2x 63 103 42 222121x x x x x评注：用零点分段法，通过零点分段将绝对值去掉，从而化简式子，解决问题是解决含绝对值问题的基本方法。

例2 已知312351312+----≥--x x xx x ，求的最大值和最小值。

(第六届迎春杯决赛试题)分析：先解不等式，求出x 的范围，然后利用绝对值的几何意义来求最大值和最小值。

解：解不等式2351312x x x --≥-- 得： 117≤x1131+--x x 的几何意义是x 到1的距离与x 到-3的距离的差，从上图中可以看出：当x ≤-3时这差取得最大值4，因117≤x ，则当117=x 时这差取得最小值1133-.评注：1、本题是采用数形结合的思想，用绝对值的几何意义来解题。

初一数学竞赛讲座(三)数字、数位及数谜问题一、一、知识要点1、整数的十进位数码表示一般地，任何一个n 位的自然数都可以表示成：122321*********a a a a a n n n n +⨯+⨯++⨯+⨯---其中，a i (i=1，2，…，n)表示数码，且0≤a i ≤9，a n ≠0.对于确定的自然数N ，它的表示是唯一的，常将这个数记为N=121a a a a n n -2、正整数指数幂的末两位数字(1) (1) 设m 、n 都是正整数，a 是m 的末位数字，那么m n 的末位数字就是a n 的末位数字。

(2) (2) 设p 、q 都是正整数，m 是任意正整数，那么m 4p+q 的末位数字与m q 的末位数字相同。

3、在与整数有关的数学问题中，有不少问题涉及到求符合一定条件的整数是多少的问题，这类问题称为数迷问题。

这类问题不需要过多的计算，只需要认真细致地分析，有时可以用“凑〞、“猜〞的方法求解，是一种有趣的数学游戏。

二、二、例题精讲例1、有一个四位数，其十位数字减去2等于个位数字，其个位数字加上2等于其百位数字，把这个四位数的四个数字反着次序排列所成的数与原数之和等于9988，求这个四位数。

分析：将这个四位数用十进位数码表示，以便利用它和它的反序数的关系列式来解决问题。

解：设所求的四位数为a ⨯103+b ⨯102+c ⨯10+d ，依题意得：(a ⨯103+b ⨯102+c ⨯10+d)+( d ⨯103+c ⨯102+b ⨯10+a)=9988∴ (a+d) ⨯103+(b+c) ⨯102+(b+c) ⨯10+ (a+d)=9988比拟等式两边首、末两位数字，得 a+d=8，于是b+c18又∵c-2=d ，d+2=b ，∴b-c=0从而解得：a=1，b=9，c=9，d=7故所求的四位数为1997评注：将整数用十进位数码表示，有助于将条件转化为等式，从而解决问题。

例2 一个正整数N 的各位数字不全相等，如果将N 的各位数字重新排列，必可得到一个最大数和一个最小数，假设最大数与最小数的差正好等于原来的数N ，那么称N 为“新生数〞，试求所有的三位“新生数〞。

全国初中数学竞赛辅导(初3)第19讲平面几何中的几个著名定理(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（全国初中数学竞赛辅导(初3)第19讲平面几何中的几个著名定理(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为全国初中数学竞赛辅导(初3)第19讲平面几何中的几个著名定理(word版可编辑修改)的全部内容。

第十九讲＊平面几何中的几个著名定理几何学起源于土地测量，几千年来，人们对几何学进行了深入的研究，现已发展成为一门具有严密的逻辑体系的数学分支．人们从少量的公理出发，经过演绎推理得到不少结论，这些结论一般就称为定理．平面几何中有不少定理，除了教科书中所阐述的一些定理外,还有许多著名的定理,以这些定理为基础，可以推出不少几何事实，得到完美的结论，以至巧妙而简捷地解决不少问题．而这些定理的证明本身，给我们许多有价值的数学思想方法，对开阔眼界、活跃思维都颇为有益．有些定理的证明方法及其引伸出的结论体现了数学的美,使人们感到对这些定理的理解也可以看作是一种享受．下面我们来介绍一些著名的定理．1．梅内劳斯定理亚历山大里亚的梅内劳斯(Menelaus，约公元100年,他和斯巴达的Menelaus是两个人）曾著《球面论》,着重讨论球面三角形的几何性质．以他的名子命名的“梅内劳斯定理"现载在初等几何和射影几何的书中，是证明点共线的重要定理．定理一直线与△ABC的三边AB，BC,CA或延长线分别相交于X，Y，Z，则证过A，B，C分别作直线XZY的垂线，设垂足分别为Q,P，S,见图3－98．由△AXQ∽△BXP得同理将这三式相乘，得说明（1)如果直线与△ABC的边都不相交，而相交在延长线上，同样可证得上述结论，但一定要有交点,且交点不在顶点上，否则定理的结论中的分母出现零，分子也出现零，这时定理的结论应改为AX×BY×CZ=XB×YC×ZA，仍然成立．(2）梅内劳斯定理的逆定理也成立，即“在△ABC的边AB和AC上分别取点X，Z，在BC的延长线上取点Y,如果那么X,Y，Z共线”．梅内劳斯定理的逆定理常被用来证明三点共线．例1 已知△ABC的内角∠B和∠C的平分线分别为BE和CF，∠A的外角平分线与BC的延长线相交于D，求证：D，E，F共线．证如图3－99有相乘后得由梅内劳斯定理的逆定理得F,D，E共线．例2（戴沙格定理)在△ABC和△A′B′C′中，若AA′,BB′，CC′相交于一点S，则AB与A′B′,BC与B′C′，AC与A′C′的交点F，D,E共线．证如图3－100,直线FA′B′截△SAB，由梅内劳斯定理有同理，直线EC′A′和DC′B′分别截△SAC和△SBC,得将这三式相乘得所以D，E，F共线．2．塞瓦定理意大利数学家塞瓦(G．Ceva)在1678年发表了下面的十分有用的定理，它是证明共点线的重要定理．定理在△ABC内任取一点P，直线AP，BP，CP分别与边BC，CA,AB相交于D，E，F,则证如图3－101，过B,C分别作直线AP的垂线，设垂足为H和K，则由于△BHD∽△CKD,所以同理可证将这三式相乘得说明 (1）如果P点在△ABC外,同样可证得上述结论,但P点不能在直线AB,BC，CA上，否则，定理的结论中的分母出现零，分子也出现零，这时，定理的结论应改为BD×CE×AF=DC×EA×FB，仍然成立．（2)塞瓦定理的逆定理也成立,即“在△ABC的边BC,CA，AB上分别取点D,E，F，如果那么直线AD，BE，CF相交于同一点．”证如图3－102，设AD和BE相交于P，作直线CP，交直线AB于F′，由塞瓦定理得所以 F′B=FB,即F′与F重合，所以AD，BE，CF相交于同一点．塞瓦定理的逆定理常被用来证明三线共点．例3 求证：三角形的三条中线、三条内角平分线和三条高所在的直线分别相交于同一点．证（1）如果D，E,F分别是△ABC的边BC,CA，AB的中点，则由塞瓦定理的逆定理得中线AD,BE,CF共点．(2)如果D，E,F分别是△ABC的内角平分线AD，BE，CF与边BC,CA，AB的交点，则由塞瓦定理的逆定理得角平分线AD，BE,CF共点．（3)设D，E,F分别是△ABC的高AD，BE，CF的垂足．(i）当△ABC是锐角三角形时(如图3－103)，D，E,F分别在BC,CA,AB上，有BD=ccosB,DC=bcosC，CE=acosc，EA=ccosA，AF=bcosA，FB=acosB，所以由塞瓦定理的逆定理得高AD，BE，CF共点．（ii)当△ABC是钝角三角形时，有BD=ccosB，DC=bcosC，CE=acosC，EA=ccos（180°-A)=-ccosA，AF=bcos(180°-A）=—bcosA,FB=acosB，所以由塞瓦定理的逆定理，得高AD,BE,CF共点．（iii）当△ABC是直角三角形时,高AD,BE，CF都经过直角顶点，所以它们共点．例4 在三角形ABC的边上向外作正方形,A1，B1，C1是正方形的边BC，CA，AB的对边的中点，证明:直线AA1,BB1,CC1相交于一点．证如图3－104．设直线AA1,BB1，CC1与边BC，CA,AB的交点分别为A2，B2，C2，那么BA2：A2C等于从点B和C到边AA1的垂线的长度之比，即其中∠θ=∠CBA1=∠BCA1．同理将上述三式相乘得根据塞瓦定理的逆定理，得AA1,BB1，CC1共点．3．斯台沃特定理定理△ABC的边BC上任取一点D，若BD=u，DC=v，AD=t，则证过A作AE⊥BC，E为垂足（如图3－105)，设DE=x，则有AE2=b2-（v-x）2=c2-(u+x）2=t2—x2，(若E在BC的延长线上，则v-x换成x—v．)于是得消去x得（u+v)2=b2u+c2v-uv(u+v)，这就是中线长公式．(2)当AD是△ABC的内角平分线时，由三角形的内角平分线的性质设a+b+c=2p，得这就是内角平分线长公式．（3)当AD是△ABC的高时，AD2=b2—u2=c2-v2．再由u+v=a,解得所以若设AD=h a，则这就是三角形的高线长公式．当D在BC的延长线上时，用—v代替v，同样可得高线长线公式．这就是三角形的面积公式．伦公式例5 如图3－106．在△ABC中，c＞b，AD是△ABC的角平分线,E在BC上，BE=CD．求证:AE2-AD2=(c-b)2．证为方便起见，设BD=u，DC=v，则BE=v，EC=u．由斯台沃特定理得所以因为AD是角平分线，所以于是4．托勒密定理托勒密(Ptolemy，约公元85~165年）是古代天文学的集大成者．一般几何教科书中的“托勒密定理”（圆内接四边形的对边积之和等于对角线之积)，实出自依巴谷(Hipparchus）之手，托勒密只是从他的书中摘出。

第一讲 有 理 数一、有理数的概念及分类。

二、有理数的计算：1、善于观察数字特征；2、灵活运用运算法则；3、掌握常用运算技巧（凑整法、分拆法等）。

三、例题示范例1、 已知数轴上有A 、B 两点，A 、B 之间的距离为1，点A 与原点O 的距离为3，那么满足条件的点B 与原点O 的距离之和等于多少？满足条件的点B 有多少个？例2、 将9998,19991998,9897,19981997----这四个数按由小到大的顺序，用“<”连结起来。

提示1：四个数都加上1不改变大小顺序；提示2：先考虑其相反数的大小顺序；提示3：考虑其倒数的大小顺序。

例3、 观察图中的数轴，用字母a 、b 、c 依次表示点A 、B 、C 对应的数。

试确定三个数ca b ab 1,1,1-的大小关系。

分析：由点B 在A 右边，知b-a >0，而A 、B 都在原点左边，故ab >0,又c >1>0,故要比较ca b ab 1,1,1-的大小关系，只要比较分母的大小关系。

例4、 在有理数a 与b(b >a)之间找出无数个有理数。

提示：P=na b a -+（n 为大于是 的自然数） 注：P 的表示方法不是唯一的。

2、符号和括号在代数运算中，添上（或去掉）括号可以改变运算的次序，从而使复杂的问题变得简单。

例5、 在数1、2、3、…、1990前添上“+”和“ —”并依次运算，所得可能的最小非负数是多少？提示：造零：n-(n+1)-(n+2)+(n+3)=0注：造零的基本技巧：两个相反数的代数和为零。

3、算对与算巧例6、 计算 -1-2-3-…-2000-2001-2002提示：1、逆序相加法。

2、求和公式：S=(首项+末项)⨯项数÷2。

例7、 计算 1+2-3-4+5+6-7-8+9+…-2000+2001+2002例8、 计算9999991999999个个个n n n +⨯ 提示1：凑整法，并运用技巧：199…9=10n +99…9，99…9=10n -1。

初中数学竞赛辅导讲义及习题解答含答案共30讲改好278页初中奥数辅导讲义培优计划（星空课堂）第一讲走进追问求根公式第二讲判别式——二次方程根的检测器第三讲充满活力的韦达定理第四讲明快简捷—构造方程的妙用第五讲一元二次方程的整数整数解第六讲转化—可化为一元二次方程的方程第七讲化归—解方程组的基本思想第八讲由常量数学到变量数学第九讲坐标平面上的直线第十讲抛物线第十一讲双曲线第十二讲方程与函数第十三讲怎样求最值第十四讲图表信息问题第十五讲统计的思想方法第十六讲锐角三角函数第十七讲解直角三角形第十八讲圆的基本性质第十九讲转化灵活的圆中角2第二十讲直线与圆第二十一讲从三角形的内切圆谈起第二十二讲园幂定理第二十三讲圆与圆第二十四讲几何的定值与最值第二十五讲辅助圆第二十六讲开放性问题评说第二十七讲动态几何问题透视第二十八讲避免漏解的奥秘第二十九讲由正难则反切入第三十讲从创新构造入手3第一讲走进追问求根公式形如a某2b某c0（a0）的方程叫一元二次方程，配方法、公式法、因式分解法是解一元二次方程的基本方法。

而公式法是解一元二次方程的最普遍、最具有一般性的方法。

求根公式某1,2bb24ac内涵丰富：它包含了初中阶段已学过的全部代数运算；它回答了2a一元二次方程的诸如怎样求实根、实根的个数、何时有实根等基本问题；它展示了数学的简洁美。

降次转化是解方程的基本思想，有些条件中含有(或可转化为)一元二次方程相关的问题，直接求解可能给解题带来许多不便，往往不是去解这个二次方程，而是对方程进行适当的变形来代换，从而使问题易于解决。

解题时常用到变形降次、整体代入、构造零值多项式等技巧与方法。

【例题求解】【例1】满足(n2n1)n21的整数n有个。

思路点拨：从指数运算律、±1的特征人手，将问题转化为解方程。

【例2】设某1、某2是二次方程某2某30的两个根，那么某134某2219的值等于（）A、一4B、8C、6D、0思路点拨：求出某1、某2的值再代入计算，则计算繁难，解题的关键是利用根的定义及变形，使多项式降次，如某123某1，某223某2。

初一数学比赛系列讲座 (7)相关恒等式的证明一、一、知识重点恒等式的证明分为一般恒等式的证明和条件恒等式证明，对于一般恒等式的证明，常常经过恒等变形从一边证到另一边，或证两边都等于同一个数或式。

在恒等变形过程中，除了要掌握一些基本方法外，还应注意应用一些变形技巧，如：整体办理、 “ 1”的代换等；对于条件恒等式的证明，怎样办理好条件等式是重点，要仔细剖析条件等式的结构特点，以及它和要证明的恒等式之间的关系。

二、二、例题精讲例 1 求证： a 1+(1-a 1)a 2+(1-a 1)(1-a 2 )a 3+ +(1-a 1)(1-a 2) (1-an-1)a n=1-(1-a )(1-a ) (1-a n-1 )(1-a n )12剖析：要证等式成立，只需证明1- a 1- (1-a 1)a 2- (1-a 1)(1-a 2)a 3 - - (1-a 1)(1-a 2) (1-a n-1)a n=(1-a 1)(1-a 2) (1-a n-1)(1-an )证明： 1- a 1- (1-a 1 )a 2- (1-a 1)(1-a 2)a 3 - - (1-a 1)(1-a 2)(1-a n-1)a n=(1-a 1)[ 1- a 2- (1-a 2 )a 3- (1-a 2)(1-a 3)a 4 - - (1-a 2)(1-a 3) (1-a n-1)a n ]=(1-a 1) (1-a 2)[ 1- a 3- (1-a 3 )a 4- (1-a 3)(1-a 4)a 5 - - (1-a 3)(1-a 4) (1-an-1)a n ]=(1-a ) (1-a ) (1-a 3 )[ 1- a 4 - (1-a )a -(1-a )(1-a )a - - (1-a )(1-a ) (1-a n-1 )a ]12454 5 6 4 5 n==(1-a 1)(1-a 2) (1-an-1)(1-an )∴ 原等式成立例 2 证明恒等式a 1a 2a na 2 a 3a 1a 2 a 1 a 2 a 3 a 2 a 3a 1 a n a 1a 1 a 1 a 2a 2 a 2 a 3a n a n a 1(第二十届全俄数学奥林匹克九年级试题 )a 1a 2a n证明a 2 a 1 a 2a 3 a 2 a 3a 1 a n a 11 111 1 1 a2 a 1 a 2 a3 a 2 a 3a 1 a n a 11 1 111 1a 1a 1 a 2a 2 a 2 a 3a na na 1a 2a 3a 1a 1 a 1 a 2a 2 a 2 a 3a n a n a 1评注：裂项是恒等变形中常用的一种方法ab c1例 3 若 abc=1，求证 aba 1 bcb 1 cac 1剖析：所要求证的等式的左侧是三个分母差别很大的式子，因此变形比较困难。