平面弯曲内力

平面弯曲的内力图绘制和弯矩图。

解：任选一截面 x ，截面法求出剪力和弯矩 x()()l x q x x M <≤02/2＝l剪力方程弯矩方程q xF s (x )M (x )0,yF=∑0,CM=∑()()s 0F x qx x l ≤<＝8/2q l 和弯矩图。

解：任选一截面 x ，截面法求出剪力和弯矩x()()l x q x x M <≤02/2＝依方程画出剪力图和弯矩图。

F sxMxql2/2q l l由内力图可见最大剪力和弯矩分别为剪力方程弯矩方程()()s 0F x qxx l ≤<＝2smax max /2F ql M ql ＝，＝例2：简支梁在C 截面处受集中力作用。

试作出其剪力图和弯矩图。

BAlF AyF Byx 2F sxMxl F b /lF a /lF a b /x 1C Fab解：由梁的平衡方程确定约束反力由截面法可以写出剪力和弯矩方程依方程画出剪力图和弯矩图。

AC :()()a x l F b x x M ≤≤1110/＝()()s 11/0F x Fb lx a <<＝00ABM M ∑∑＝，＝CB : ()()()l x alx l F a x M ≤≤-222/＝()()s 22/F x Fa l a x l -<<＝//Ay By F Fb l F Fa l＝，＝()-()+()+ BAlF A yF B yx 2lM a /x 1lM /lM b / CMab例3：简支梁在C 截面处受集中力偶作用。

试作出其剪力图和弯矩图。

0＝，＝∑∑B A M M 依方程画出剪力图和弯矩图。

解：由梁的平衡方程确定约束反力由截面法可以写出剪力和弯矩方程AC :()()a x lM x x M <≤1110/＝()()s 11/0F x M lx a <≤＝CB :()()bx lM x x M <≤-2220/＝()()s 22/0F x M lx b <≤＝/-/Ay By F M l F M l＝，＝。

第七章平面弯曲内力一、教学目标和教学内容1、教学目标⑴掌握弯曲变形与平面弯曲等基本概念；⑵熟练掌握用截面法求弯曲内力；⑶熟练列出剪力方程和弯矩方程并绘制剪力图和弯矩图；⑷利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图；⑸掌握叠加法绘制剪力图和弯矩图。

2、教学内容⑴平面弯曲等基本概念；⑵截面法及简便方法求弯曲内力；⑶剪力方程和弯矩方程、绘制剪力图和弯矩图；⑷用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图；⑸叠加法绘制剪力图和弯矩图。

二、重点难点1、平面弯曲的概念；2、剪力和弯矩，剪力和弯矩的正负符号规则；3、剪力图和弯矩图；4、剪力、弯矩和载荷集度的微分、积分关系；5、叠加法绘制剪力图和弯矩图。

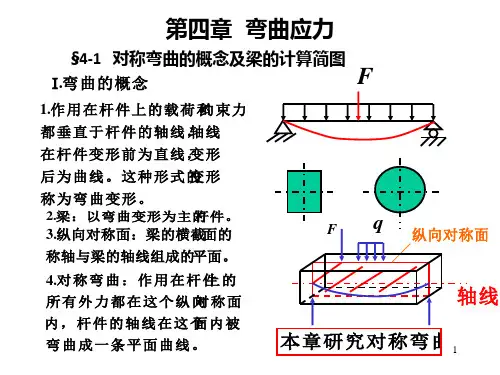
三、学时分配：4学时一、平面弯曲概念和实例弯曲：讨论杆的弯曲暂时限制在如下的范围；①杆的横截面至少有一根对称轴（一个对称面）图6-4②载荷作用在对称平面内在此前提下，可讨论杆件弯曲的受力特点：所有外力都作用在通过杆件轴线的纵向对称平面内：变形特点：杆件轴线在载荷作用平面内弯成一条曲线。

受力、变形具有上述特点的弯曲称为平面弯曲。

⑵何谓梁？凡是以弯曲为主要变形的杆件，通常称为梁。

⑶梁的种类：①简支梁②悬臂梁③外伸梁二、平面弯曲内力⑴梁的内力—剪力与弯矩①确定约束反力②内力分析用截面法沿m-m截面截开（任取一段）F,M。

按平衡的概念标上sF--与横截面相切—剪力sM—内力偶矩—弯矩③内力值的确定用静力平衡条件：0=∑y F 0=-Q A F F 得 A s F F =0=∑o M 0=-⋅M a F A 得 a F M A ⋅=（O-- 截面形心）⑵剪力、弯矩的正、负号规定：剪力：当截面上的FQ 使该截面邻近微段有做顺时针转动趋势时为正，反之为负。

弯矩：当截面上的弯矩使该截面的邻近微段下部受拉，上部受压为正（即凹向上时为正），反之为负。

小结①求指定截面上的内力时，既可取梁的左段为脱离体，也可取右段为脱离体，两者计算结果一致（方向、转向相反）。

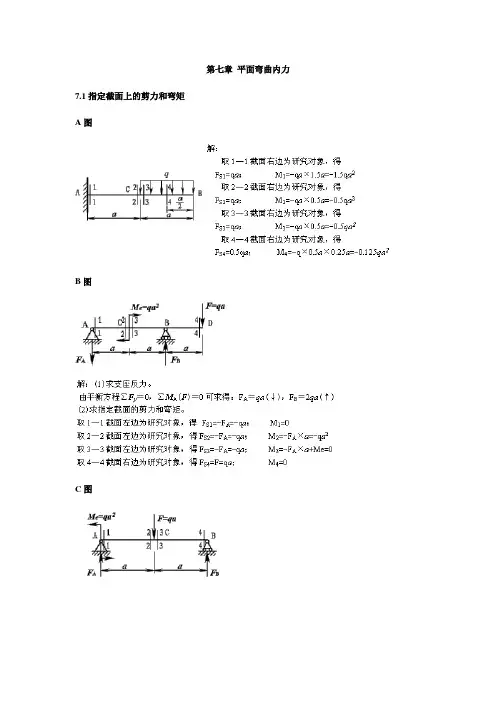
第七章平面弯曲内力7.1指定截面上的剪力和弯矩A图B图C图D图7.2画剪力图和弯矩图A图B图7.3梁的剪力图和弯矩图解：（1）由静力平衡方程得：F A=F，M A= Fa，方向如图所示。

（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。

（3）梁最大绝对值剪力在AB段内截面，大小为2F。

梁最大绝对值弯矩在C截面，大小为2Fa。

B图解：（1）由静力平衡方程得：F A=3q l/8（↑），F B=q l/8（↑）。

（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。

（3）梁的最大绝对值剪力在A右截面，大小为3q l/8。

梁的最大弯矩绝对值在距A端3l/8处截面，大小为9q l2/128。

解：（1）由静力平衡方程得：F B=2qa，M B=qa2，方向如图所示。

（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。

（3）梁的最大绝对值剪力在B左截面，大小为2qa。

梁的最大绝对值弯矩在距AC段内和B左截面，大小为qa2。

D图解：（1）由静力平衡方程得：F A=qa/2（↓），F B= qa/2（↓）。

（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。

（3）梁的最大绝对值剪力在AC和DB 段内，大小为qa/2。

梁的最大弯矩绝对值在AB跨中间截面，大小为5qa2/8。

解：（1）由静力平衡方程得：F A=9qa/4（↑），F B= 3qa/4（↑）。

（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。

（3）梁最大绝对值剪力在A右截面，大小为5qa/4。

梁最大弯矩绝对值在A截面，大小为qa2/2。

F图解：（1）由静力平衡方程得：F A=F（↑），F B= 3F（↑）。

（2）利用M，F S，q之间的关系分段作剪力图和弯矩图。

（3）梁最大绝对值剪力在DB段内截面，大小为3F。

梁最大弯矩绝对值在D截面，大小为3Fa。

G图解：（1）由静力平衡方程得：F A=4.5qa（↑），F B= 0.5qa（↑）。

平面弯曲梁求内力的方法平面弯曲梁是一种常见的结构形式，广泛应用于建筑、桥梁、机械等领域。

在设计和使用过程中，需要对其内力进行分析和计算，以保证结构的安全性和稳定性。

本文将介绍平面弯曲梁求内力的方法。

一、平面弯曲梁的基本概念平面弯曲梁是指在平面内受到弯曲作用的梁，其截面形状可以是任意形状，但要求在弯曲过程中截面形状不变。

平面弯曲梁的内力主要包括弯矩、剪力和轴力。

弯矩是指在梁的截面上由于弯曲作用而产生的力矩，其大小与梁的曲率半径和截面惯性矩有关。

剪力是指在梁的截面上由于剪切作用而产生的力，其大小与梁的截面形状和受力情况有关。

轴力是指在梁的轴线方向上由于拉伸或压缩作用而产生的力，其大小与梁的受力情况有关。

二、平面弯曲梁的内力分析方法平面弯曲梁的内力分析方法主要有两种，即弯矩法和剪力法。

下面将分别介绍这两种方法的基本原理和计算步骤。

1. 弯矩法弯矩法是指通过计算梁的弯矩分布来求解梁的内力。

其基本原理是根据梁的受力情况和截面形状，计算出梁的弯矩分布，并根据弯矩方程求解出梁的内力。

计算步骤如下：（1）确定梁的受力情况，包括支座反力和外载荷。

（2）根据梁的几何形状和受力情况，计算出梁的弯矩分布。

（3）根据弯矩方程求解出梁的内力。

弯矩方程是指在梁的任意一点处，弯矩与该点处的曲率半径和截面惯性矩之间的关系式。

对于一般的平面弯曲梁，弯矩方程可以表示为：M = EIκ其中，M为弯矩，E为弹性模量，I为截面惯性矩，κ为曲率。

2. 剪力法剪力法是指通过计算梁的剪力分布来求解梁的内力。

其基本原理是根据梁的受力情况和截面形状，计算出梁的剪力分布，并根据剪力方程求解出梁的内力。

计算步骤如下：（1）确定梁的受力情况，包括支座反力和外载荷。

（2）根据梁的几何形状和受力情况，计算出梁的剪力分布。

（3）根据剪力方程求解出梁的内力。

剪力方程是指在梁的任意一点处，剪力与该点处的截面形状和受力情况之间的关系式。

对于一般的平面弯曲梁，剪力方程可以表示为：V = dM/dx其中，V为剪力，M为弯矩，x为梁的坐标。