当前位置：文档之家 › 理论力学-动量矩定理2

理论力学-动量矩定理2

  • 格式：ppt
  • 大小：617.00 KB
  • 文档页数：1

下载文档原格式

  / 1

合集下载

第十三章动量矩定理_理论力学

第十三章动量矩定理_理论力学

式中
分别为作用于质点上的内力和外力。求 n 个方程的矢量和有
式中
，
于 点的主矩。交换左端求和及求导的次序，有
为作用于系统上的外力系对
令 （13-3）
为质系中各质点的动量对 点之矩的矢量和，或质系动量对于 点的主矩，称为质系对 点的动量矩。由此得
（13-4） 式（13-4）为质系动量矩定理，即：质系对固定点 的动量矩对于时间的一阶导数等于外力 系对同一点的主矩。
设 Q 为体积流量， 为密度， 和 分别为水流进口处和出口处的绝对速度， 和 分别为涡轮外圆和内圆的半径， 为 与涡轮外圆切线的夹角， 为 与涡轮内圆切线的
夹角，则
由动量矩定理 得
为叶片作用于水流上的力矩。若水涡轮共有 个叶片，则水流作用于涡轮的转动力矩为
方向与图示方向相反。 §13-2 刚体绕定轴转动微分方程
解：取两叶片间的水流为研究对象（图 13-4 中的兰色部分）。作用于质系上的的外力有 重力和叶片的约束力，重力平行于 z 轴，对转动轴之矩为零。所以外力主矩为叶片对水流
的约束力对 z 轴之矩 。
计算 时间间隔内动量矩的增量 。设 t 瞬时占据 ABCD 的水流，经过 时间间隔
后，运动至占据
，设流动是稳定的，则
有
式中
得
（13-8）
或
（13-9）
此式称为刚体绕定轴转动的微分方程。
为刚体绕定轴转动的角加速度，所以上式
可写为
（13-10）
1．由于约束力对 z 轴的力矩为零，所以方程中只需考虑主动力的矩。 2．比较刚体绕定轴转动微分方程与刚体平动微分方程，即
与
形式相似，求解问题的方法和步骤也相似。 转动惯量与质量都是刚体惯性的度量，转动惯量在刚体转动时起作用，质量在刚体平动

理论力学动量矩定理

理论力学动量矩定理

四. 平行移轴定理
刚体对某轴的转动惯量等于刚体对通过质心且与该轴平行 的轴的转动惯量，加上刚体的质量与两轴间距离的平方之乘积。
J z ' J zC m d 2
证明：设刚体的质量为m，质心为C。
O ' z '//Cz
J zC mi ri 2 mi ( xi 2 yi 2 )
J z ' mi ri ' 2 mi ( xi ' 2 yi ' 2 )
xi xi ', yi ' yi d
J z ' mi [ xi 2 ( yi d )2 ]
mi ( xi 2 yi 2 ) ( mi )d 2 2d mi yi
质点对O点的动量矩与对 z 轴的动量矩之间的关系：
M O (mv )
注意：要求 z 轴通过O点。
z
M z (mv )
二．质点系的动量矩
质点系对O点动量矩： LO 质点系对 z 轴动量矩： 同样有关系式： 例：平动刚体的动量矩。
M
O
Lz M z (mi vi )
(mv i i ) r i mv i i
( e)
PA PB d g ( d t r PA PB P / 2
）
[例4] 已知猴子A重=猴子B重，初始静止，后猴B以相对绳 速度 v 上爬，猴A相对绳不动。问猴B向上爬时，猴A将如何 动？动的速度多大？（轮重不计）
解： 设猴A向上的绝对速度为 vA，则
猴B向上的绝对速度为 vB= vvA 。
平动刚体对固定点（轴）的动量矩就等于刚体质心的动量 对该点（轴）的动量矩。

理论力学-动量矩定理

理论力学-动量矩定理

d rC d vC vC , aC , dt dt
n d LC ri Fi e dt i
vC vC 0 ,
m a C Fie
n dLC M C (Fie ) dt i
相对质心的动量矩定理
质点系相对质心的动量矩定理
n n d LC e e ri Fi M C ( Fi ) i dt i
m v
i
i
m vC
LO rC m vC LC
相对质心的动量矩定理
质点系相对质心的动量矩定理
根据上式和质点系对固定点的动量矩定理，
n d LO d ( rC m vC LC ) ri Fi e dt dt i
ri rC rr
n n d rC d vC d LC e rC Fi ri Fi e m vC rC m dt dt dt i i
即有
LC ri mi vir
相对质心的动量矩定理
质点系相对质心的动量矩
质点系相对固定点的动量矩与质点系相对质心的动量矩 之间存在确定的关系。 质点系相对固定点的动量矩为
LO ri mi vi
i
因为 所以有 因为 所以有
ri rC rr
LO rC mi v i ri mi v i
刚体定轴转动微分方程
例 题 1
图示钟摆简化模型中，已知均质细杆 和均质圆盘的质量分别为m1 、m2 ，杆 长为l，圆盘直径为d。
ϕ
试求：钟摆作小摆动时的周期。 解：摆绕O轴作定轴转动。设ϕ 为任意 时刻转过的角度，规定逆时针为正。根 据定轴转动的微分方程
J z M z

理论力学动量矩定理

理论力学动量矩定理

12.2 动量矩定理
12.2.1 质点旳动量矩定理
设质点对固定点O旳动 量矩为MO(mv)，作用力F对 同一点旳矩为MO(F) ，如图 所示。
将动量矩对时间取一 次导数，得
d dt
MO
(mv)
d dt
(r
mv)
d r mv r d (mv)
dt
dt
MO(mv) MO(F)
x
z
F mv
Q
r
y
12.2.1 质点旳动量矩定理
将上式投影在直角坐标轴上，并将对点旳动量矩与对轴 旳动量矩旳关系代入，得
d dt
M
x
(mv)
M
x
(F
)
d dt
M
y
(mv)
M
y
(F
)
d dt
M
z
(mv)
M
z
(F
)
质点对某固定
轴旳动量矩对时间旳 一阶导数等于质点所 受旳力对同一轴旳矩。
12.2.1 质点旳动量矩定理
例12-2 图示为一单摆（数学摆），摆锤质量为m，摆线长为 l，如给摆锤以初位移或初速度（统称初扰动），它就在经过 O点旳铅垂平面内摆动。求此单摆在微小摆动时旳运动规律。
例12-1 均质圆盘可绕轴O转动，其上缠有一 绳，绳下端吊一重物A。若圆盘对转轴O旳转
动惯量为J，半径为r，角速度为，重物A旳
质量为m，并设绳与圆盘间无相对滑动，求系 统对轴O旳动量矩。
解：
LO L块 L盘 mvr J mr 2 J (mr 2 J )
LO旳转向沿逆时针方向。
Or
A mv
LO J m2vR MO (F (e) ) M m2 g sin R

理论力学：动量矩定理

理论力学：动量矩定理
பைடு நூலகம்
y’
2020/12/9
Fe maA aA mg
B
A
FN 1
F1
FN 2
x’
F2
10
理论力学
§6-2 动量矩定理
例：滑块A可在光滑水平面上滑动，为使AB杆以匀角速度 绕
铰链A转动，求作用在AB杆上的力偶M。设：m1 m2 m, AB L
y
FN
解：1、取滑块A和小球B为研究对象
2、受力分析与运动分析
m1 m2
2020/12/9
11
理论力学
§6-2 动量矩定理
y FAy
A
o
FAx aA xA x
3、研究AB杆和小球B，受力分析 4、应用相对动轴A的动量矩定理
dLrA
dt
n
M A (Fi(e) )
i1
rAC (maA )
A
M
杆相对A轴的动量矩
LrA m2L2
B m2xA 外力对A轴之矩
问题：若滑块不脱离地面，试确定AB杆的最大角速度。
2020/12/9
13
理论力学
§6-2 动量矩定理
2020/12/9
14
理论力学
§6-2 动量矩定理
思考题：图示系统中，系统结 构不同，求解方法是否相同？
m1 A
M
m1 A
M
m2
B
2020/12/9
m1 A
M
m2
R
m3 B
m2 B
15
理论力学
§6-2 动量矩定理
mg
B
AB L
2020/12/9
§6-2 动量矩定理
L
3(g 2

第12章-动量矩定理

第12章-动量矩定理
它表达为刚体质量 m 与某一长度ρ z 旳平方
旳乘积： J z m z2
细直杆 均质圆环 均质圆板
J z /m 1 / 3 l2 z 0.5774 l
J z /m R2 z R
J z /m 1 / 2 R2 z 0.7071R
z 假如把刚体旳质量全部集中在与 轴相距为ρ z 旳点
上，则此质点对 z 轴旳转动惯量与原刚体相同。
四、平行轴定理
J z J z md 2
定理：刚体对任意轴旳转动惯量，等于刚体对 于经过质心、并与该轴平行旳轴旳转动惯量， 加上刚体旳质量与两轴间距离平方旳乘积。
z
O
z
d
ri
ri
C
O
mi
zi
y( y)
C点为质心；
O z 为质心轴，O z
为与之平行旳任
xi
一轴，距离为 d 。
x d x yi J z mi ri2 mi ( xi2 yi2 )
d dt
(
J
z
)
Jz
Mz
dω dt
(Fi
)M
M z (Fi )
z
(
FN
i
)
Fi
或
Jz
d2
dt2
M z (Fi )
或 J z M z (Fi )
FNi
与 m a Fi 比较
例：已知滑轮半径为 R ，转动惯量为 J ，带动滑轮
旳皮带拉力分别为 F1 和 F2 。求滑轮旳角加速度 。
F2 解：根据定轴转动微分方程
d(ri
mivi ) dt
ri
F (e) i
ri
Fi(i)
(i 1,2,, n)
相加得

动量矩定理公式

动量矩定理公式

动量矩定理公式动量矩定理公式是经典力学中最为重要的定理之一，也是描述质点、力和角动量之间关系的基本公式。

它在物理学和工程学中的应用非常广泛，例如在机械设计中，我们需要利用动量矩定理公式来计算旋转惯量、角加速度等参数，以便进行机器的性能设计和优化。

在本文中，我们将深入探讨动量矩定理公式的含义、意义和应用。

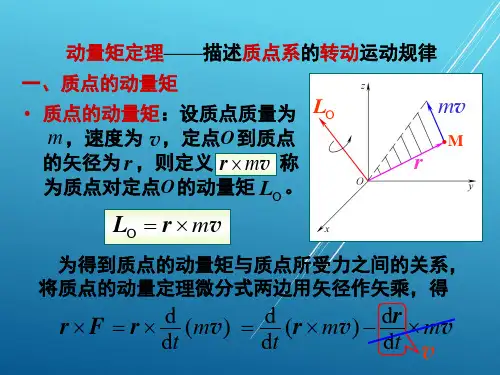
一、动量矩定理的定义动量矩定理公式是描述质点或物体角动量的变化率与施加于物体的力矩之间的关系。

在经典力学中，动量矩定理的形式可以表示为：L = Iω其中，L 表示物体的角动量，I 表示物体的旋转惯量，ω 表示物体的角速度。

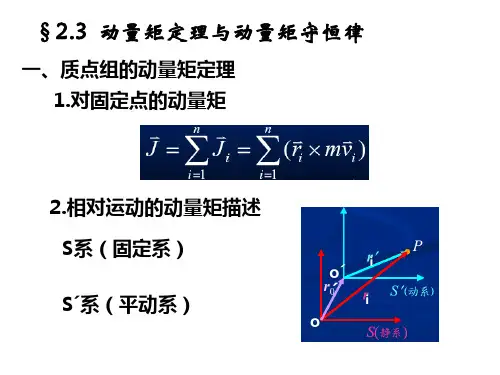
动量矩定理的本质是质点或物体的动量守恒定律和角动量守恒定律的延伸和综合。

动量守恒定律和角动量守恒定律分别是描述质点和物体在运动过程中动量和角动量不变的规律。

而动量矩定理则是将它们集成在一起，明确了物体动量和角动量与施加于它的力和力矩之间的关系。

在动量矩定理中，旋转惯量起到了很重要的作用。

旋转惯量是物体绕不同轴旋转时所具有的转动惯性，是物体旋转惯性的度量。

不同形状和密度的物体，其旋转惯量也会有所不同。

例如，某个物体绕它的质心旋转时，它的旋转惯量是最小的。

因为在质心系下，物体的动量为零，只有转动部分的动量和角动量。

二、动量矩定理的应用动量矩定理的具体应用非常广泛。

下面将分别就质点的动量矩定理、刚体的动量矩定理以及动量与角动量的守恒作一些说明。

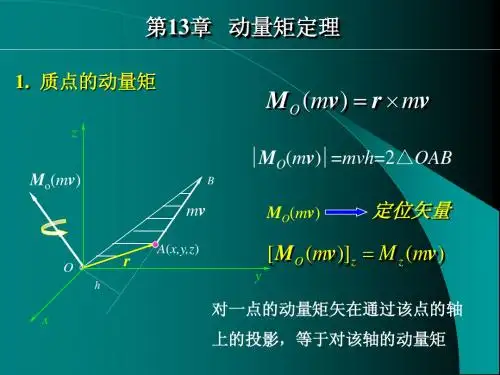
1. 质点的动量矩定理对于一个质量为 m 的质点，在施加力 F 时，它的动量矩定理为：Ft = Δ(mv)其中，Ft 为施加于物体上的力矩，v 表示质点的速度，Δ(mv) 表示质点动量的变化。

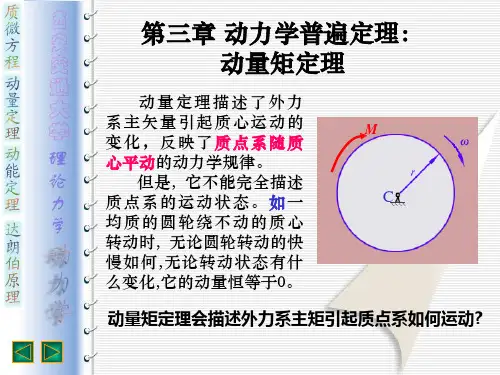
2. 刚体的动量矩定理对于一个刚体在施加力矩 M 时，它的动量矩定理可以表示为：M = Iα其中，M 为施加于刚体上的力矩，I 表示刚体的转动惯量，α 表示刚体的角加速度。

在实际应用中，我们经常需要利用动量矩定理来计算旋转惯量、角加速度等参数。

例如，当我们想设计一个能够快速旋转的机器时，就需要通过动量矩定理来确定机器的转动惯量和角加速度等参数，并根据这些参数来设计机器的各个部分。

理论力学第1节 动量矩定理

理论力学第1节 动量矩定理
i 1
d Lx dt

n

M
x
( Fi ( e )
)
i 1
dM y dt

n

M
y
( Fi ( e )
)
i 1
dLz dt

n

M
z
( Fi ( e )
)
i 1
质点系对某轴的动量矩对时间的导数等于作用于 质点系上的外力对该轴之矩的矢量和。
• 质点系对固定点的动量矩守恒：当作用在质点系的 外力对某固定点之矩的矢量和为零，质点系对该点 的动量矩保持不变。
记 J z miri2
称刚体对z轴 的转动惯量
• 质量连续分布刚体的转动惯量公式
说明
Jz M r2dm
刚体对轴的转动惯量取决于刚体质量的大小、质量 的分布情况及转轴的位置，而与其运动状态无关。
对形状不规则物体的转动惯量常用实验方法测得。
冰上芭蕾 舞演员旋转 时，通过张 开、收拢两 臂来改变自 身质量对垂 直轴的转动 惯量，以达 到改变转动 速度的目的
r O
M
设 v 为物体A、B的瞬时速度，
为圆盘的角速度，两者的关系为：
v r
系统对O轴的动量矩：
LO mAvr mBvr JO 其中
B AJOΒιβλιοθήκη 1 2Mr 2
LO

mA vr

mBvr

1 2
Mr 2

mA
vr

mB
vr

1 2
Mrv
系统外力对O轴的力矩为：
M O mA gr mBgr
质点对 O 点动量矩的矢量和
C mi

理论力学第13章动量矩定理

理论力学第13章动量矩定理

mi
rC x′
C
y′ y
mi vi mvC
LC ri mi vi
x
LO rC mvC LC
LO rC mvC LC
dLO d (e) (rC mvC LC ) r i Fi dt dt
r i rC ri
drC dLC d (e) i Fi ( e ) mvC rC mvC r C Fi r dt dt dt
v R
应用动量矩定理
O

FOx
mg
M
(e)
WR
dLO (e ) M dt
WR 2 a W 2 (JO R ) g
P
v
JO W dv ( R) WR R g dt
W
z
例 题3
z
求：此时系统的角速度 解：取系统为研究对象
M
A
(e ) z
0
A
B
a l
a
B
Lz 恒量


l
由质心坐标公式，有
z
vi z′ ri r′ i rC x′
C
mi
y′ y
O
mi ri mrC 0
x
LC ri mi vir
§13-6 刚体的平面运动微分方程
LC J C
由质心运动定理和相对于质 心的动量矩定理，有：
y
Fn
y′
D
F2 F1
maC Fi ( e ) d (e) J C J C M C ( Fi ) dt
用于质点系的外力对质心的主矩 ，这就是质点系相对于质心(平移
系)的动量矩定理。

理论力学第二章 质点组力学-2)

理论力学第二章 质点组力学-2)

m222
0
0
m1gl
cos
(4)
联立方程(1)(2)(3)(4)解得
1x
2m22 gl sin
m1 m2 m1tg 2 m2 sec2
1y
2 m1 m2 gl sin
m1 m2 sin2
2
u
2m12 gl sin
m1 m2 m1tg 2 m2 sec2
ax
m m
ax
g
g
二人均以匀加速向上爬
t
2
t2
2s ax 2s ax
t t
t
ax
2ms ms m m g
m m sg ms ms
注：也可用对通 过滑轮中心水平 轴的动量矩定理
质量不等的两人能同时到达顶端的前提条件
ax 0, ax 0
即
ms ms, 且 m m 或ms ms,且 m m
i 1
i 1
i 1
i 1
3.在质心系中分析以上四项
s´系的原点固定在质点组的质心上，则：
第一项：
rvo rvc ,vo vc , rvc 0
n (rvo m ivo ) n (rvc m ivc ) rvc n m ivc 对o点的动量矩
求和后，
i 1, n
叙述:质点组动能的微分等于质点组所受的外力与内 力的元功之和。
特点：①内力所作的功不能互相抵消。
②质点组不受外力或合外力为零，动能不一定守恒。
三、质点组对质心的动能定理 质点组内力做功
引入质心参照系，质点组中第i个质点的动能
d
(1 2
mii2
)
v F (e)
i
drvi
v F (i)

理论力学之动量矩定理

理论力学之动量矩定理

证明 过固定点O建立固定坐标系 Oxyz，以质点系的质心 C为
z
原点，取平动坐标系Cx y z ,它以质心的速度vC 运动。
ri rc rri 质心的性质 vi vc vri
z' A vr v vC vC y y'
mi ri mi rri rc rc 0 M M 定系 动系 Mvc mi vi mi vri 0
rC
C
x'
rr
O
质点系内任一质点 A的绝对速度 v=ve+vr=vc+vr , 则质点系对固定点O的动量矩
x

(r
LO
C
mi vi )
(r m v ) [(r
i
(r
i i
C
rri ) mi vi ]
ri mi v C )
(r
ri mi v ri )
d M O (mv ) M O ( F ) dt
质点对固定点的动量矩对时间的一阶导数等 于作用于质点上的力对同一点的力矩。
B 固定轴
d M O (mv ) M O ( F ) dt
(将上式两边分别向坐标轴投影，再利用对点和 对轴动量矩公式可得)： d M x (mv ) M x ( F ) dt d M y (mv) M y (F ) dt d M z (mv) M z (F ) dt 质点对某固定轴的动量矩对时间的导数，等于作用 于该质点的所有力对于同一轴之矩的代数和。 质点对定点的动量矩定理在三个坐 标轴的投影方程不独立
O
A
mivi
ri
LO =∑ MO(mivi) = ∑(miri )×vC 又因为 (∑mi )rC = ∑miri 所以 LO = ∑mi rC ×vC=rC× (∑mi )vC

合肥工业大学《理论力学》l第十二章动量矩定理

合肥工业大学《理论力学》l第十二章动量矩定理

Mz
ε
ε∝ Mz
当Mz= 0 时， ε= 0，刚体作匀速转动或静止。
刚体转动惯量的大小表现了刚体转动状态改变 的难易程度转。动惯量是刚体转动时的惯性度量。
请比较 Jz = ∑Mz 与 m a = ∑F 。
§4 刚体对轴的转动惯量
一、转动惯量的概念
转动惯量是刚体转动时的惯性度量， 它 等 于 刚 体内各质点的质量与质点到轴的垂直距离平方 的乘积之和，即
z
解：分析小球受力。
r2 B
∵ ∑MZ(F(e)) = 0， ∴ LZ = const ! 初瞬时(A处)，
v2 F
r1
T
LZA = mv1r1， B处， LZB = mv2r2， ∴ mv1r1 = mv2r2
A mg v1
而 r1 =2r2 得 v2 = 2v1
解毕。
二、质点系的动量矩定理
设质点系由n个质点组成，第i个质点的质量为mi， 速度为vi， 受力：外力Fi(e) 、内力Fi(i) ，则 根 据 质 点 的动量矩定理，有
d dt
Mo
(mi vi
)
Mo
( Fi ( i )
)
Mo
( Fi ( e )
)
对于n个质点，有n个这样的方程，将这些方程求和，
则
内力系主矢 = 0
n
i1
d dt
Mo (mivi )
n i1
Mo (Fi(i) )
n i1
Mo (Fi(e) )
所以得
ddtindd1tMin1o
M(moi
v(mi )i
Lz=Jzω
§2 动量矩定理
一、质点的动量矩定理
zF
B
设质点质量为m，受力F， MO(mv)

理论力学第2节 质点系相对于质心的动量矩定理

理论力学第2节 质点系相对于质心的动量矩定理

LC (ri mivi ) (ri mivir )
结 论 LC (ri mivi ) (ri mivir )
计算质点系相对于质心的动量矩，用绝对速度和相 对速度结果都是一样的。对一般运动的质点系，通常 可以分解为随质心的平移和绕质心的转动，因此，用 相对速度计算质点系相对质心的动量矩往往更方便。
i 1
dLC dt
n
ri Fi(e)
i 1
或
dLC dt
n
MC (Fi(e) )
i 1
质点系相对于质心的动量矩定理表明：质点系相 对于质心的动量矩对时间的导数，等于作用于质点系 的外力对质心的主矩。该定理在形式上与质点系相对 固定点的动量矩定理完全相同。
dLC dt
n
ri Fi(e)
i 1
或
dLC dt
n
MC (Fi(e) )
i 1
注意
质点系相对于质心的动量矩定理所涉及的随质 心运动的动坐标系，一定是平移坐标系，定理只适 用于质心这个特殊的动点。对于其他动点，定理将 出现附加项或附加条件。
• 质点系相对于质心的动量矩定理
质点系的 动量矩定理
定点动量矩与相对于 质心动量矩间的关系
dLO dt
n
MO (Fi(e) )
i 1
LO rC MvC LC
dLO dt

d dt
(rC MvC
n
LC ) ri பைடு நூலகம் Fi(e)
i 1
将 ri rC ri代入得
• 质点系对定点动量矩与相对于质心动量矩间的关系
在固定参考系Oxyz中，质点系对固定点O的动量矩为

《理论力学》第十一章 动量矩定理

《理论力学》第十一章 动量矩定理

LO lOi ri mi v i
将动量矩投影到以O为原点的直角坐标轴上
HOHAI UNIVERSITY ENGINEERING MECHANICS
Lx l x mv m yv z zv y
L y l y mv m zv x xv z Lz l z mv m xv y yv x
（二）质点系的动量矩L
设质点系由n个质点组成，其中第i个质点 的质量为mi，速度为vi。 质系对任意固定点O的动量矩：
HOHAI UNIVERSITY ENGINEERING MECHANICS
LO lOi ri mi v i
质系对任意固定点O的动量矩为各质点 的动量对O点矩的矢量和。
3、刚体动量矩的计算
1）刚体平动
HOHAI UNIVERSITY ENGINEERING MECHANICS
HOHAI UNIVERSITY ENGINEERING MECHANICS
例1：均质细长直杆长l，质量m1，与质量为m2,半径
为r，均质圆盘固结。已知角速度为,试求对转轴的 动量矩。 解：
HOHAI UNIVERSITY ENGINEERING MECHANICS
第十一章
HOHAI UNIVERSITY ENGINEERING MECHANICS
动量矩定理
§1 动量矩（表征物体转动的物理量）
一、动量矩的定义及计算
1. 对任意固定点O的动量矩（矢量）：
质点对固定点的动量矩即质点的动量对固定点的矩： z lO r mv r p mv lo M r F
平轴z的转动惯量。轴z过O点垂直纸面

11-2 动量矩定理

11-2 动量矩定理

d LO = dt
∑ MO (Fi(e) )
—
质点系的动量矩定理
质点系对某定点O 的动量矩对时间
的一阶导数，等于作用于质点系的外力对
O点之矩的矢量和。
投影形式：
d Lx
dt
d Ly dt
= M x (Fi (e) )
= M y (Fi (e) )
d Lz dt
= M z (Fi (e) )
⑶ 摆捶对O轴的动量矩
M O (mv) = mv ⋅l
= (mlϕ) ⋅l = ml 2ϕ
摆捶外力对O轴的力矩 M O (F ) = −mg ⋅l sinϕ
⑷ 由摆捶对O轴的动量矩定理得
d dt
M
O
(mv)
=
M
O
(F
)
⇒
ml
2ϕ
=
−mg
⋅
l
sin
ϕOϕ Fm ⋅ (lϕ) mg
ml2ϕ = −mg ⋅l sin ϕ
= Mx(F)
= M y(F)
= Mz(F)
质点对某定轴的动量矩对时间的一阶导数，
等于作用力对同一轴之矩。
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
例题
一单摆在平面内小幅度摆动,摆绳长l,摆捶质量为m,求摆捶微小摆动的运动方程。
解：⑴ 取摆捶为研究对象,画受力图
⑵ 运动分析 v = lω = lϕ
v
θ m2 g
ω
O
FOy
FOx M m1 g
L=O (J + m2R2 )v R
∑ MO (Fi(e) ) = M − (m2 g sinθ ) ⋅ R
三、动量矩守恒定律
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

LC J C
刚体平面运动微分方程
LC J C
xC yC
其中JC为刚体对通过质心C 且与运动平面垂直的轴的转 动惯量， 为角速度。
当作用于刚体上的力系等价于质量对称面内的一个平面 力系时，对刚体平面运动，应用质心运动定理和相对质心 动量矩定理 ，有 n maC Fie i n J C M C (Fie ) i
刚体平面运动微分方程
C*
vA 相对特殊瞬心的动量矩定理：平面 运动过程中，如果刚体的质心 C 到速 度瞬心 C* 的距离保持不变，则质点 系相对速度瞬心的动量矩对时间的导 vB 数等于质点系外力对同一点的主矩。 即
aC
FN
maC mgsin F
0 mgcos FN
J C Fr
刚体平面运动微分方程
α
F
maC mgsin F
（） 1
0 mgcos FN
（2）
aC
FN
J C Fr
运动学补充关系
（3）
（4）
1 2 aC 1 mr 2 maC 2 2 r
质点系相对固定点的动量矩与质点系相对质心的动量矩 之间存在确定的关系。 质点系相对固定点的动量矩为
LO ri mi vi
i
因为 所以有 因为 所以有
ri Байду номын сангаас rC rr
LO rC mi v i ri mi v i
m v
i
i
m vC
LO rC m vC LC
0 mgcos FN
1 F mgsin FN f s 3 1 f smin tan 3 此即圆轮在斜面上不滑动的最小静摩擦因数。
刚体平面运动微分方程
均质杆 AB长为l，放放置于铅垂 平面内，杆一端A靠在光滑的铅垂 墙上，另一端B放在光滑的水平面 上，与水平面的夹角为 0 。然后 ，令杆由静止状态滑下。 求：杆在任意位置时的角加速度。
第11章 动量矩定理

刚体平面运动微分方程
刚体平面运动微分方程
取质心 C 为基点，其坐标为 xC、yC，设D为刚体上任意一点 ， CD 与 x 轴的夹角为 φ, 则刚体 的位置可由xC、yC和φ确定。
xC
yC
将刚体的运动分解为随质心的平移和绕质心的转动两部 分。当刚体具有质量对称面、且质量对称面平行于运动平 面时，则在固连于质心的平移参考系中，刚体对质心的动 量矩为
刚体平面运动微分方程
maC Fie i n J C M C (Fie ) i
n
mxC Fxe
或者
e myC Fy J C M c ( Fi e )
这就是刚体平面运动的微分方程。 需要指出的是，如果上述投影方程中各式等号的左侧各项 均恒等于零，则得到静力学中平面力系的平衡方程，即外力 系的主矢、主矩均等于零。因此，质点系动量定理与动量矩 定理，不但完全确定了刚体一般运动的动力学方程，而且还 完成了对刚体平面运动的特例—— 平衡情形的静力学描述。
相对质心的动量矩定理
在质点系相对于惯性参考系中固定点（或固定 轴）的动量矩定理中，动量矩由系统的绝对运动 所确定。 这里讨论质点系相对于质点系的质心或通过质 心的动轴的动量矩定理，一方面是因为它有广泛 的应用价值，另一方面动量矩定理仍保持了简单 的形式。
相对质心的动量矩定理
质点系相对质心的动量矩
d rC d vC vC , aC , dt dt
n d LC ri Fi e dt i
vC vC 0 ,
m a C Fie
n dLC M C (Fie ) dt i
相对质心的动量矩定理
质点系相对质心的动量矩定理
n n d LC e e ri Fi M C ( Fi ) i dt i
这就是质点系相对质心的动量矩定理(theorem of the moment of momentum with respect to the center of mass) ，它表明：质点 系相对质心的动量矩对时间的导数，等于作用于质点系的外力 对质心的主矩。 需要注意的是，这里所涉及的随质心运动的动坐标系，一定 是平移坐标系。定理只适用于质心这一特殊的动点，对其它动 点，定理将出现附加项。 对于刚体，质心运动定理建立了外力与质心运动的关系；质 点系相对质心的动量矩定理建立了外力与刚体在平移参考系内 绕质心转动的关系。
相对质心的动量矩定理
质点系相对质心的动量矩定理
根据上式和质点系对固定点的动量矩定理，
n d LO d ( rC m vC LC ) ri Fi e dt dt i
ri rC rr
n n d rC d vC d LC e rC Fi ri Fi e m vC rC m dt dt dt i i
刚体平面运动微分方程
解：以杆为研究对象，杆作 平面运动，分析其受力 列出平面运动微分方程 mg
maCx FA maCy FB mg J C FB l l cos 0 FA sin 0 2 2
FA
FB
式中有五个未知量 ( aCx , aCy , , FA , FB ) ，如果要 求得全部未知量，还需两个运动学补充方程。显然，这 一方法比较麻烦。
aC r
（4）式代入（3）式，得 代入（1）式，得
F JC

r

aC
2 gsin 3
刚体平面运动微分方程
α
F
解：2．确定圆轮在斜面上不滑动的 最小静摩擦因数
2 aC gsin 3
F JC

r
aC
FN

1 2 aC 1 mr 2 maC 2 2 r
1 F mgsin FN f s 3
刚体平面运动微分方程
半径为 r 的匀质圆盘从静止开 始，沿倾角为θ的斜面无滑动的滚 下。 试求： 1 ．圆轮滚至任意位置时的质心 加速度 aC ； 2 ．圆轮在斜面上不打滑的最小 静摩擦因数。
刚体平面运动微分方程
解：分析圆轮受力
α
F
1．确定圆轮质心的加速度 圆轮作平面运动。根据刚 体平面运动微分方程，有