理论力学课后习题答案第9章动量矩定理及其应用)
- 格式:doc
- 大小:893.50 KB
- 文档页数:11

论力学课后习题答案-第8章--动量定理及其应用第8章 动量定理及其应用8-1 计算下列图示情况下系统的动量。
(1) 已知OA =AB =l ,θ=45°,ω为常量,均质连杆AB 的质量为m ,而曲柄OA 和滑块B 的质量不计(图a )。
(2) 质量均为m 的均质细杆AB 、BC 和均质圆盘CD 用铰链联结在一起并支承如图。
已知AB = BC = CD = 2R ,图示瞬时A 、B 、C 处于同一水平直线位置,而CD 铅直,AB 杆以角速度ω转动(图b )。
(3) 图示小球M 质量为m 1,固结在长为l 、质量为m 2的均质细杆OM 上,杆的一端O 铰接在不计质量且以速度v 运动的小车上,杆OM 以角速度ω绕O 轴转动(图c )。
解:(1)p = mv C =ωm l 25,方向同Cv (解图(a ));(2)p = mv C 1 + mv C 2 = mv B = 2Rm ω,方向同Bv ,垂直AC (解图(b )); (3)j i p )60sin 260sin ()]60cos 2()60cos ([2121︒+︒+︒-+︒-=ωωωωlm l m l v m l v m j i 423]42)[(212121m m l l m m v m m +++-+=ωω(解图(c ))。
习题8-1图ABOθω ABCDωOMvω 60˚(a)(b)(c)8-2 图示机构中,已知均质杆AB 质量为m ,长为l ;均质杆BC 质量为4m ,长为2l 。
图示瞬时AB 杆的角速度为ω,求此时系统的动量。
解:杆BC 瞬时平移,其速度为v Bωωωm l m l l m p p p BCAB 2942=+=+= 方向同v B 。
8-3 两均质杆AC 和BC 的质量分别为m 1和m 2,在C 点用铰链连接,两杆立于铅垂平面内,如图所示。
设地面光滑,两杆在图示位置无初速倒向地面。
问:当m 1= m 2和m 1= 2m 2时,点C 的运动轨迹是否相同。

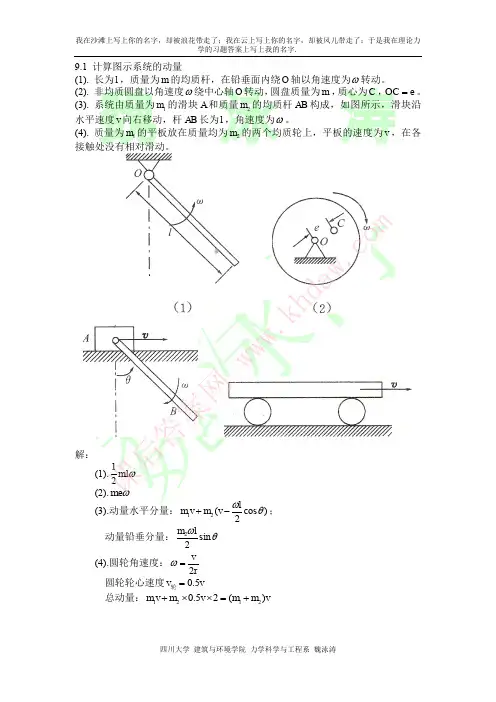


9- 1 在图示系统中,均质杆OA 、AB 与均质轮的质量均为m ,OA杆的长度为l 1,AB 杆的长度为l 2,轮的半径为R ,轮沿水平面作纯转动。
在图示刹时,OA 杆的角速度为,求整个系统的动量。
5ml1,方向水平向左2题9-1图题 9-2图9- 2 如下图,均质圆盘半径为R,质量为 m ,不计质量的细杆长l ,绕轴O转动,角速度为,求以下三种状况下圆盘对固定轴的动量矩:(a)圆盘固结于杆;(b)圆环绕 A 轴转动,相关于杆OA 的角速度为;(c)圆环绕 A 轴转动,相关于杆OA 的角速度为。
(a)L O m(R2l 2 );( b)L O ml 2;( c)L O m( R2l 2 ) 29- 3 水平圆盘可绕铅直轴z 转动,如下图,其对z 轴的转动惯量为J z。
一质量为m的质点,在圆盘上作匀速圆周运动,质点的速度为 v0,圆的半径为r,圆心到盘中心的距离为l。
开始运动时,质点在地点M 0,圆盘角速度为零。
求圆盘角速度与角间的关系,轴承摩擦不计。
9- 4 如下图,质量为m 的滑块 A,能够在水平圆滑槽中运动,拥有刚性系数为k 的弹簧一端与滑块相连结,另一端固定。
杆AB 长度为 l,质量忽视不计, A 端与滑块 A 铰接,B端装有质量 m1,在铅直平面内可绕点 A 旋转。
设在力偶 M 作用下转动角速度为常数。
求滑块 A 的运动微分方程。
x k x m1l2 sin tm m1m m19- 5 质量为 m ,半径为平板与地面间摩擦系数为R 的均质圆盘,置于质量为M 的平板上,沿平板加一常力F。
设f,平板与圆盘间的接触是足够粗拙的,求圆盘中心 A 点的加快度。
9- 6 均质实心圆柱体 A 和薄铁环 B 的质量均为m,半径都等于r ,二者用杆AB 铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为,如下图。
如杆的质量忽视不计,求杆AB 的加快度和杆的内力。
a 4 g sin;79- 7 均质圆柱体 A 和 B 的质量均为m,半径为r ,一绳缠在绕固定轴O 转动的圆柱 A 上,绳的另一端绕在圆柱 B 上,如下图。

第九章平衡问题——能量方法 习题解答9-1质量为3 kg 的质点以5 m/s 的速度沿水平直线向左运动。
今对其施以水平向右的的常力,此力的作用经30 s 而停止,这时质点的速度水平向右,大小为55 m/s 。
求此力的大小及其所做的功。
解:取质点m 为研究对象。
由质点动量定理;()12v v F -=m t :()12v v m Ft +=,解得:()())N (630555312=+=+=t v v m F .由质点动能定理; ()())J (450055532121222122=-⨯⨯=-==v v m Fs W .9-2如图所示,一弹簧振子沿倾角为ϑ的斜面滑动,已知物块重G ,弹簧刚度系数为k ,动摩擦因数为f ;求从弹簧原长压缩s 的路程中所有力的功及从压缩s 再回弹λ的过程中所有力的功。
解:取物块为研究对象。
物块受到重力G ,弹簧力F ,斜面摩擦力m ax F 和法向反力N F 作用,其中仅法向反力N F 不作功。
在弹簧压缩过程中,所有力的功为 ()221cos sin ks s f G W --=ϑϑ 在弹簧压缩s 再回弹λ的过程中,所有力的功为 ()()[]2221cos sin λλϑϑ--+--=s s k f G W 。
9-3弹簧原长l ,刚度系数为k ,一端固定在O 点,此点在半径为r = l 的圆周上。
如弹簧的另一端由图示的B 点拉至A 点,求弹簧力所做的功。
AC ⊥BC ,OA 为直径。
解:在B 点弹簧的变形为()l 121-=λ,在A 点弹簧的变形为l =2λ。
弹簧力所做的功为()()222211221kl k W --=-=λλ。
9-4图示机构在力F 1和F 2作用下在图示位置平衡,不计各构件自重和各处摩擦,OD=BD=l 1,AD=l 2。
求F 1/F 2的值。
解:用解析法解题。
()j i F ϑϑcos sin 11-=F , i F 22F = 点A 和B 的坐标及其变分为()()j i r ϑϑsin cos 2121l l l l A ++--= ,i r ϑcos 21l B -=题9-2图题9-3图质点的受力图()()j i r δϑϑδϑϑ⋅++⋅-=cos sin δ2121l l l l A ,i r δϑϑ⋅=sin 2δ1l B 。

理论力学习题解答第九章题9-2图9-2 如图所示,均质圆盘半径为R,质量为m ,不计质量的细杆长,绕轴O转动,角速度为,求下列三种情况下圆盘对固定轴的动量矩:(a)圆盘固结于杆;(b)圆盘绕A轴转动,相对于杆OA的角速度为;(c)圆盘绕A轴转动,相对于杆OA的角速度为。
(a);(b);(c)9-3水平圆盘可绕铅直轴转动,如图所示,其对轴的转动惯量为。
一质量为m的质点,在圆盘上作匀速圆周运动,质点的速度为,圆的半径为r,圆心到盘中心的距离为。
开始运动时,质点在位置,圆盘角速度为零。
求圆盘角速度与角间的关系,轴承摩擦不计。
9-4如图所示,质量为m的滑块A,可以在水平光滑槽中运动,具有刚性系数为k的弹簧一端与滑块相连接,另一端固定。
杆AB长度为l,质量忽略不计,A端与滑块A铰接,B端装有质量,在铅直平面内可绕点A旋转。
设在力偶M作用下转动角速度为常数。
求滑块A的运动微分方程。
9-5质量为m ,半径为R的均质圆盘,置于质量为M的平板上,沿平板加一常力F。
设平板与地面间摩擦系数为f,平板与圆盘间的接触是足够粗糙的,求圆盘中心A点的加速度。
9-6均质实心圆柱体A和薄铁环B的质量均为m,半径都等于r,两者用杆AB铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为,如图所示。
如杆的质量忽略不计,求杆AB的加速度和杆的内力。
;9-7均质圆柱体A和B的质量均为m,半径为r,一绳缠在绕固定轴O转动的圆柱A上,绳的另一端绕在圆柱B上,如图所示。
摩擦不计。
求:(1)圆柱体B下落时质心的加速度;(2)若在圆柱体A上作用一逆时针转向,矩为M 的力偶,试问在什么条件下圆柱体B的质心加速度将向上。
9-8平面机构由两匀质杆AB,BO组成,两杆的质量均为m,长度均为l,在铅垂平面内运动。
在杆AB上作用一不变的力偶矩M,从图示位置由静止开始运动。
不计摩擦,试求当A即将碰到铰支座O时A 端的速度。
9-9长为l、质量为m的均质杆OA以球铰链O固定,并以等角速度绕铅直线转动,如图所示。



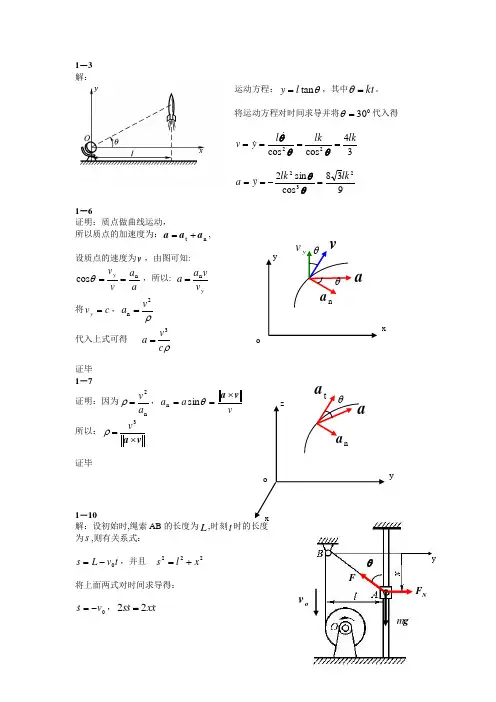
1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lk lk l y v ====θθθ938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以质点的加速度为:n t a a a +=,设质点的速度为v ,由图可知:a a v v yn cos ==θ,所以: yv va a n =将c v y =,ρ2n va =代入上式可得 ρc v a 3=证毕 1-7证明:因为n2a v =ρ,v a a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10 解:设初始时,绳索AB 的长度为L ,时刻t 时的长度为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= ,x x s s 22= xyoan avy vθθtayzoan aθxovovF N Fg myθ由此解得:xsv x 0-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得:2002v v s x x x=-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-== (负号说明滑块A 的加速度向上)取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的运动微分方程:N F F ym F mg xm +-=-=θθsin cos其中:2222sin ,cos l x l lx x +=+=θθ0,3220=-=yx l v x将其代入直角坐标形式的运动微分方程可得:23220)(1)(x lxl v g m F ++=1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即:θcos A B v v = (a ) 因为x R x 22cos -=θ (b )将上式代入(a )式得到A 点速度的大小为:22R x xRv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x x ω=--22 ,将该式两边平方可得:222222)(x R R x xω=-将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=--将上式消去x 2后,可求得:22242)(R x xR x--=ω (d)由上式可知滑块A 的加速度方向向左,其大小为 22242)(R x xR a A -=ω取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的 运动微分方程:mg F F ym F xm N -+=-=θθsin cos其中:x R x xR22cos ,sin -==θθ, 0,)(22242=--=y R x x R x ω将其代入直角坐标形式的运动微分方程可得2525)(,)(225222242R x x R m mg F R x x R m F N --=-=ωω1-13解:动点:套筒A ;动系:OC 杆;定系:机座;xθ AvAω ONF BRg mFyavevr v运动分析:绝对运动:直线运动;相对运动:直线运动;牵连运动:定轴转动。
(a)A(a)O第10章 动能定理及其应用10-1 计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A 、B 两点的速度方向如图示,B 点的速度为v B ,θ = 45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v(图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.222222163)2(2121)2(212121BB BC C C mv r v mr v m J mv T =⋅+=+=ω 2.222122222214321)(21212121v m v m r v r m v m v m T +=⋅++=3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2 图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a )B A T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ,角速度为ω,齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。
O ωRr ABθ习题9-2图习题20-3图OxF Oy F gm Ddα习题20-3解图第9章 动量矩定理及其应用9-1 计算下列情形下系统的动量矩。
1. 圆盘以ω的角速度绕O 轴转动,质量为m 的小球M 可沿圆盘的径向凹槽运动,图示瞬时小球以相对于圆盘的速度v r 运动到OM = s 处(图a );求小球对O 点的动量矩。
2. 图示质量为m 的偏心轮在水平面上作平面运动。
轮心为A ,质心为C ,且AC = e ;轮子半径为R ,对轮心A 的转动惯量为J A ;C 、A 、B 三点在同一铅垂线上(图b )。
(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对B 点的动量矩;(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对B 点的动量矩。
解:1、2s m L O ω=(逆)2、(1))1()(Remv e v m mv p A A C +=+==ω(逆)Rv me J R e R mv J e R mv L A A AC C B )()()(22-++=++=ω (2))(e v m mv p A C ω+==ωωωω)()()())(()(2meR J v e R m me J e R e v m J e R mv L A A A A C C B +++=-+++=++=9-2 图示系统中,已知鼓轮以ω的角速度绕O 轴转动,其大、小半径分别为R 、r ,对O 轴的转动惯量为J O ;物块A 、B 的质量分别为m A 和m B ;试求系统对O 轴的动量矩。
解:ω)(22r m R m J L B A O O ++=9-3 图示匀质细杆OA 和EC 的质量分别为50kg 和100kg ,并在点A 焊成一体。
若此结构在图示位置由静止状态释放,计算刚释放时,杆的角加速度及铰链O 处的约束力。
不计铰链摩擦。
解:令m = m OA = 50 kg ,则m EC = 2m 质心D 位置:(设l = 1 m) m 6565===l OD d 刚体作定轴转动,初瞬时ω=0 l mg lmg J O ⋅+⋅=22α 222232)2(212131ml ml l m ml J O =+⋅⋅+= 即mgl ml 2532=α2rad/s 17.865==g l αgl a D 362565t =⋅=α 由质心运动定理: Oy D F mg a m -=⋅33t4491211362533==-=mg g mmg F Oy N (↑) 0=ω,0n=D a , 0=Ox F(a)OMvωωA BC Rv A(b)习题9-1图(b ) 习题9-5解图J习题9-5图9-4 卷扬机机构如图所示。
可绕固定轴转动的轮B 、C ,其半径分别为R 和r ,对自身转轴的转动惯量分别为J 1和J 2。
被提升重物A 的质量为m ,作用于轮C 的主动转矩为M ,求重物A 的加速度。
解:对轮C :r F M J C T 2-=α对轮B 和重物A :mgR R F mR J -'=+T 21)(α运动学关系:ααR r a C ==2222212)(rmR R J r J rR mgr M a ++-=9-5 图示电动绞车提升一质量为m 的物体,在其主动轴上作用一矩为M 力偶。
已知主动轴和从动轴连同安装在这两轴上的齿轮以及其它附属零件对各自转动轴的转动惯量分别为J 1和J 2;传动比r 2 : r 1 = i ;吊索缠绕在鼓轮上,此轮半径为R 。
设轴承的摩擦和吊索的质量忽略不计,求重物的加速度。
解:对轮1(图a ):111Fr M J -=α对轮2(图b ):mgR r F mR J -'=+2222)(α 2211ααr r =;21ααi =21222iJ mR J mgRMi ++-=α 重物的加速度:21222)(i J mR J RmgR Mi R a ++-==α9-6 均质细杆长2l ,质量为m ,放在两个支承A 和B 上,如图所示。
杆的质心C 到两支承的距离相等,即AC = CB = e 。
现在突然移去支承B ,求在刚移去支承B 瞬时支承A 上压力的改变量ΔF A 。
解:mge J A =α,mge me ml =+α)31(22A C F mg ma -=22233e l ge e a C +==α 22233e l mge mg F A +-= mge l l e mg e l mge F mg F A A )3(2323322222222+-=-+=-=∆习题9-6图习题9-4图习题9-6解图习题9-7图习题9-8图dB ACgm lF(b) 习题9-7解图Agm CθB..θrd +9-7 为了求得连杆的转动惯量,用一细圆杆穿过十字头销A 处的衬套管,并使连杆绕这细杆的水平轴线摆动,如图a 、b 所示。
摆动100次所用的时间为100s 。
另外,如图c 所示,为了求得连杆重心到悬挂轴的距离AC = d ,将连杆水平放置,在点A 处用杆悬挂,点B 放置于台秤上,台秤的读数F = 490N 。
已知连杆质量为80kg ,A 与B 间的距离l =1m ,十字头销的半径r = 40mm 。
试求连杆对于通过质心C 并垂直于图面的轴的转动惯量J C 。
解:图(a ),1<<θ时,θθ)(r d mg J A +-= 0)(=++θθr d mg J A 0)(=++θθAJ r d mg AJ r d mg )(n +=ω )(π2π2n r d mg J T A+==ω (1) 2)(r d m J J C A ++= (2)由图(b ):0=∑A M ,625.085===mg Fl d m代入(1)、(2),注意到周期s 2=T ,得22222m kg 45.17)665.0π8.9(665.080)](π)[()(π)(⋅=-⨯⨯=+-+=+-+=r d g r d m r d m r d mg J C9-8 图示圆柱体A 的质量为m ,在其中部绕以细绳,绳的一端B 固定。
圆柱体沿绳子解开的而降落,其初速为零。
求当圆柱体的轴降落了高度h 时圆柱体中心A 的速度υ和绳子的拉力F T 。
解:法1:图(a ) T F mg ma A -= (1) r F αJ A T = (2) r αa A = (3)221mr J A = 解得 mg F 31T=(拉) g a A 32=(常量)(4)习题9-10图ORr F θ习题9-9图AαAv Aa rCTF gm(a)由运动学 gh h a v A A 3322==(↓) 法2:由于动瞬心与轮的质心距离保持不变,故可对瞬心C 用动量矩定理:mgr J C =ϕ (5) 2223mr mr J J A C =+=又 ra A=ϕg a A 32=(同式(4)) 再由 T F mg ma A -= 得 mg F 31T=(拉) gh h a v A A 3322==(↓)9-9 鼓轮如图,其外、内半径分别为R 和r ,质量为m ,对质心轴O 的回转半径为ρ,且ρ2= R ·r ,鼓轮在拉力F 的作用下沿倾角为θ的斜面往上纯滚动,F 力与斜面平行,不计滚动摩阻。
试求质心O 的加速度。
解:鼓轮作平面运动,轴O 沿斜面作直线运动:θsin f mg F F ma O --= (1) R F Fr m f 2+=αρ(2) 纯滚:αR a O =(3)代入(2)R F Fr Ra m O f 2+=⋅ρ (4)解(1)、(4)联立,消去F f ,得)(sin )(222ρθ+-+=R m mgR r R FR a O9-10 图示重物A 的质量为m ,当其下降时,借无重且不可伸长的绳使滚子C 沿水平轨道滚动而不滑动。
绳子跨过不计质量的定滑轮D 并绕在滑轮B 上。
滑轮B 与滚子C 固结为一体。
已知滑轮B 的半径为R ,滚子C 的半径为r ,二者总质量为m ′,其对与图面垂直的轴O 的回转半径为ρ。
求:重物A 的加速度。
O Rr FθF f F N m g习题9-11图DABC习题9-12图rαD NF Fagm MM f(a)解:法1:对轮: Fr TR J O -=α (1)T F a m O -='(2) 对A :T mg ma A -=(3)又:tH H A a a a ==绳以O 为基点:tn n t HO HO O H H a a a a a ++=+ααα)(tt r R r R a a a O HO H -=-=-=(→)α)(r R a A -=(↓)(4)由上四式联立,得(注意到2ρm J O '=)1)()()()()(2222222+-+⋅'=-++'-=r R r m m gr R m r m r R mg a A ρρ法2:对瞬心E 用动量矩定理(本题质心瞬心之距离为常数))(r R T J E -=α T mg ma A -= 又α)(r R a A -=)(222r m r m J J O E +'='+=ρ 可解得:1)()(222+-+⋅'=r R r m m ga A ρ9-11 图示匀质圆柱体质量为m ,半径为r ,在力偶作用下沿水平面作纯滚动。
若力偶的力偶矩M 为常数,滚动阻碍系数为δ,求圆柱中心O 的加速度及其与地面的静滑动摩擦力。
解:f M M J D -=α (1)N f F M δ= mg F =N223mr J D =ra =α代入(1),得mrmg M a 3)(2δ-=又:F ma =rmg M F 3)(2δ-=9-12 跨过定滑轮D 的细绳,一端缠绕在均质圆柱体A 上,另一端系在光滑水平面上的物体B 上,如图所示。
已知圆柱A 的半径为r ,质量为m 1;物块B 的质量为m 2。
试求物块B 和圆柱质心C 的加速度以及绳索的拉力。
滑轮D 和细绳的质量以及轴承摩擦忽略不计。
解:对轮C : r F J C T =αT 11F g m a m C -=对物块B :T 2F a m B = 且:αr a a B C +=;2121r m J C =解得:g m m m a B2113+= ;g m m m a C 212132++= g m m m m F 2121T 3+=HOOHO an H anHO atH a (b)m F 绳H a HT 'g mOT(a)a AF N ·Em ′gNF αagm 1F O(a)xθAF ..Cy ..Cx αA C BBF gm O(b)AαCθPgm BBAF(a)9-13 图示匀质圆轮的质量为m ,半径为r ,静止地放置在水平胶带上。