周期问题

周期性问题练习题
1. 小明每周存储100元到他的储蓄账户中。

如果他的储蓄账户的年利率是5%，请问1年后他的账户总额是多少？
2. 一辆汽车每隔3个月来一次保养，上一次保养的时间是1月1号，那么下一次保养的时间是什么时候？
3. 某工厂的产量每年以8%的速度递增。

如果今年的产量是1000个产品，那么明年的产量预计是多少？
4. 张三每天都做相同的运动训练，并且每7天就会感觉疲劳一次。

如果他从1月1号开始训练，那么第一次感觉疲劳的时间是什么时候？
5. 使用一个周期为30天的计划表，标记每个重复的周期的第一天为“Day 1”。

那么40天后，应该标记为第几天？
6. 一家超市每隔一周会进行一次促销活动，从每周的星期一开始算起，请问下一次促销活动将在星期几举行？
以上是一些周期性问题练习题，你可以尝试用相关的计算方法和技巧来解答。

通过反复练习，你可以进一步提高对周期性问题的理解和解决能力。

祝你成功！。

1.【2015年江苏省】，那么⼩数点后⾯的第个数字是（ ）。

A.B.C.D.2.【2016年全国】的商⽤循环⼩数表⽰，这个⼩数的⼩数点后⾯第位数字是（ ）A.B.C.D.3.【2016年浙江省】⼀辆⻓途客⻋从武汉开往潜江，再从潜江开往武汉，不断往返．⻓途客⻋⾏驶次后在（ ）。

A.武汉B.潜江C.不能确定4.【2016年全国】体育课上同学们站成⼀排，⽼师让他们按、、、、循环报数，最后⼀个报的数是，这⼀排同学可能有（ ）⼈。

A.B.C.5.【2015年福建省泉州市南安市】年⽉⽇是星期⼆，同年的⽉⽇是( )。

A.星期四B.星期五C.星期六6.【2015年江苏省】☆☆☆□□○☆☆☆□□○☆☆☆□□○…，照这样排列下去，左边起第个1÷14=0.0714285714285⋯6207145÷7200712520121234522627282008112139C.○D.⽆法判断7.【2014年安徽省池州市⽯台县】⼀排学⽣从前往后按、、、、、依次重复报数，从前往后数⼩明是第个，他应该报（ ）A.B.C.8.【2012年全国】年的⽉⽇是星期五，下个星期五是（ ）A.⽉⽇B.⽉⽇C.⽉⽇9.【2015年江苏省】⼩红要为妈妈穿⼀串圆形珠链．她想⽤⿊⽩两种颜⾊的珠⼦穿，且每两颗⽩珠⼦之间穿颗⿊珠⼦。

穿成这串珠链⾄少需（ ）颗珠⼦。

A.B.C.D.10.【2017年全国】有⼀排彩旗，按照⾯红旗、⾯⻩旗、⾯绿旗的顺序排列，第⾯是（ ）旗。

A.红B.⻩C.绿11.【2015年江苏省】年元旦是星期⽇，那年元旦是星期（ ）。

A.⼆B.三123123⋯24123201122532333456712141231002012201312.【2016年⼴西省百⾊市隆林各族⾃治县】为了迎接检查，学校在操场上按照红、⻩、绿的顺序布置了很多花，第盆是（ ）花。

A.红B.⻩C.绿13.【2017年全国】年⽉⽇是星期四，年⽉⽇是星期( )。

周期问题（一）我们知道，一年有12个月，从一月开始，一月、二月、三月、……十二月；每周有七天，从星期一开始，星期一、星期二、……星期天。

在日常生活中有许多类似这样重复出现的现象，一些数、图形的变化也是周而复始地循环出现的，我们把这种特殊的规律性问题称为周期问题。

解答这类题目只有找到规律，才能获得正确的方法。

例1．●●○●●○●●○……上面黑、白两色小球按照一定的规律排列着，其中第90个是（ ）例2．有同样大小的红、白黑珠共150个，按先5个红的，再4个白的，再3个黑的排列着。

第144个珠是什么颜色？例3．有249朵花，按5朵红花、9朵黄花、13朵绿花的顺序排列，最后一朵花是什么颜色的？例4．有同样大小的红、黄、蓝弹子共180个，按先4个红的，再2个黄的，再3个蓝的排列着。

三种颜色的弹子各有多少个？ 例5．上表中，将每列上下两个字组成一组，例如，第一组为（共，社），第二组为（产，会），那么，第128组是（ ）练习与思考1．根据图中物体的排列规律，填空。

(2)□○△□○△…… 第55个是（ ）2.把1～100号的卡片依次发给小红、小芳、小华、小明四个人，已知1号发绘小红，16号发给谁？38号呢？ 3．四（1）班六位同学在进行报数游戏，他们围成一圈，小娟报“1”，小华报“2”，小丽报“3”，小勇报“4”，小强报“5”，小琳报“6”，每位报的数总比前一位多1。

“72”是谁报的？“190”呢？ 4．一些黑白珠子按一定规律排列（如图），如果这些珠子共有50个，则倒数第六个珠子是什么颜色？●●●○●●●○●●●○……5．有同样大小的红、白、黑珠共90个，按先3个红的，后2个白的，再1个黑的排列。

黑珠共有几个？第68个珠子是什么颜色？6．有100朵花，按4朵红花，3朵绿花，5朵黄花，2朵紫花的顺序排列，最后一朵是什么颜色的花？四种花各有几朵？7．第26列的字母和数字各是什么？B ）， 第26组是什么？周期问题（二）例1．10个2连乘的积的个位数是几？例2．1998年元旦是星期四，1999年元旦是星期几？ 例3．黑珠、白珠共185个串成一串，排列如图：○●○○○●○○○●○○○……例4．把自然数按下图的规律排列后，分成A 、B 、C 、D 、E 五类，例如，4在D 类，10在B 类。

简单的周期问题例1：找出以下图形排列的规律，根据规律算出第16个图形是什么？〔1〕□△△□△△□△△□△△……〔2〕☆○○△☆○○△☆○○△……例2：一串珠子，按图2-1排列，那么第33颗是什么珠子？第48颗是什么珠子？例3：国庆节挂彩灯，按“红黄、蓝、白、绿、紫〞的顺序挂，一共挂了50只彩灯，第50只彩灯是什么颜色的？红色的彩灯一共有多少只？例4：有一列数：1,3,5,1,3,5,1,3,5,……〔1〕第26个数是几？〔2〕这26个数的和是多少？例5：今年“六一〞儿童节是星期三，再过16天是星期几？例6：胡老师把1～40号拼音卡片，依次发给小伟、小冬、小军、小辉和小燕，问第27张卡片应发给谁？练习1、按下面图形的排列情况，算出第20个图形是什么？〔1〕△○○△○○△○○……〔2〕□△○△□△○△□△○△……〔3〕☆△△□○☆△△□○☆△△□○……〔4〕○△△☆☆☆○△△☆☆☆……2、丽丽用一根绳子穿珠子。

珠子有黑白两色。

她先穿1颗黑珠子，再穿2颗白珠子，以后都按1颗黑珠子2颗白珠子这样的规律穿下去。

等穿完20颗时，最后一颗是什么颜色的珠子？3、学校大门有一串彩灯，按“红、黄、绿、白〞的规律排列起来，请你算一算，第13只彩灯是什么颜色？第18只和第24只彩灯分别是什么颜色？4、植树节那天，同学们按1棵松树，2棵香樟树、3棵广玉兰栽树，第15棵树是什么树？第30棵树又是什么树？5、学校开运动会，在操场四周插彩旗，见图2-2，从主席台左边起，第13面是什么颜色？最后一面是什么颜色？6、二年级同学参加学校拔河比赛，他们比赛的队伍按“两男三女〞依次排成一队，第23个同学是男同学还是女同学？第32个同学是男同学还是女同学？7、一只走马灯有四个面，每一面上都画着一匹马，第一面马抬左前腿，第二面马抬右后腿，第三面马抬右前腿，第四面马抬左后腿。

看灯的小朋友从第一面起，等转到第十九面时，看到的马是什么姿势的？8、明明在桌上摆了一排硬币，按一枚1元，两枚5角和两枚1角的次序排列，共放了19枚硬币。

周期问题知识要点：1、周期问题：一些数、图形和事物的变化往往是周而复始循环出现的，我们把具有这种规律的问题称为周期问题。

例如每隔7天是一周，则说周期是7；每隔12个月是一年，则说周期是12；每隔24小时是一昼夜，则说周期是24等。

2、在研究这些简单周期问题时，我们首先要仔细审题，判断其不断重复出现的规律，也就是找出循环的固定数，如果正好有个整数周期，结果为周期里的最后一个；如果不是从第一个开始循环，利用除法算式求出余数，最后根据余数的大小得出正确的结果。

3、解决周期问题的方法：首先要发现问题的周期性和确定周期长度。

然后用画图、列举、计算等方法解决有关问题。

课前一练1、如图电子跳蚤每跳一步，可以从一个圆圈跳到相邻的圆圈；现在，一只红跳蚤从标有数“1”的圆圈按顺时针方向跳了20步，落在一个圆圈里；一只黑跳蚤也从标有数“1”的圆圈起跳，但它是沿着逆时针方向跳了24步落在另一个圆圈里，那么这两个圆圈里的乘积是多少？2、如下图有一串珠子按2粒白珠、3粒黑珠依次用线串出来，第32粒珠是什么颜色的，几个白球，几个黑球？○○●●●○○●●●○○●●●○○……思维拓展例题1、假设所有的自然数排列起来，如下所示，39应该排在哪个字母下面？88应该排在哪个字母下面？A B C D1 2 3 45 6 7 89 10 11 1213 14 15 16………………解析：从排列情况可以知道，这些自然数是按从小到大按照ABCDABCD……循环排列的,即是4个数为一周期，我们可以根据这些数除以4所得的余数来分析、判断。

39÷9=4……3 88÷4=22所以，39应该排在第4行第3个字母C下面，88应排在第22行第1个字母A 下面。

小窍门：找周期长度，再用总数除以周期长度，看余数。

练习：1、假设所有自然数排列起来，如下图所示，36、43、78、2000应分别排在哪个字母下面？A B C1 2 34 5 67 8 910 11 12……………2、按表中的顺序排下去，数“1998”在下面两个表中各出现在哪个字母的位置上？A B C D1 2 3 45 6 78 9 10 1112 13 14…………例题2过大年过大年过大……发压岁钱发压岁钱……上表是中，每一列两字组成一组，如第一组“过，发”，第二组“大，压”，……问第20个组是什么，几个“大”字，几个“发”字？解析：观察上表，发现有两个独立的排列规律。

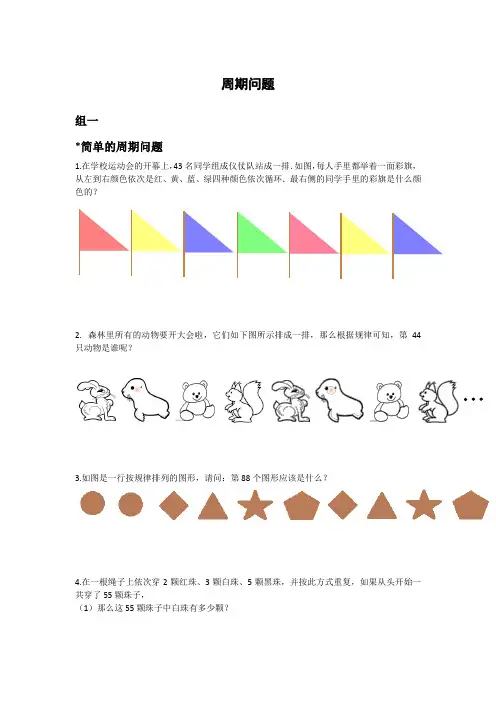
周期问题组一*简单的周期问题1.在学校运动会的开幕上，43名同学组成仪仗队站成一排．如图，每人手里都举着一面彩旗，从左到右颜色依次是红、黄、蓝、绿四种颜色依次循环．最右侧的同学手里的彩旗是什么颜色的？2.森林里所有的动物要开大会啦，它们如下图所示排成一排，那么根据规律可知，第44只动物是谁呢？3.如图是一行按规律排列的图形，请问：第88个图形应该是什么？4.在一根绳子上依次穿2颗红珠、3颗白珠、5颗黑珠，并按此方式重复，如果从头开始一共穿了55颗珠子，（1）那么这55颗珠子中白珠有多少颗？（2）那么这55颗珠子中白珠比黑珠少多少颗？组二*较复杂的周期问题1.如图，16幅图按规律排成一排，其中前三幅图已经画出，请按规律画出第16幅图的样子．2.将一些自然数排成一列，其中任意相邻的五个数之和都等于15．已知第一个数等于1，第二个数等于2，第三个数等于3，第四个数等于4．问：（1）请写出这个数列的前十个数；（2）第一百个数等于多少？3.个507777⨯⨯⨯⨯所得积的末位数是（）4.紧接着1989后面一串数字，写下的每个数字都是它前面两个数字的乘积的个位数．例如8×9=72，在9后面写2，9×2=18，在2后面写8…得到一串数字：1 9 8 92 8 6…这串数字从1开始往右数，第60个数字是什么？三.家庭作业1. 如图，由一系列黑、白三角形按一定的规律排成一行．请问:第25个图形应该是什么样子？2.. 观察图中黑、白两色三角形的变化规律，请问：前100个图形中有多少个白色三角形？3..个252222⨯⨯⨯⨯的乘积末位数字是多少？。

周期问题一、概念和原理周期现象：事物在运动变化过程中，某些特征有规律循环出现；周期：我们把连续两次出现所经过的时间叫周期；解决有关周期性问题的关键是确定循环周期.分类： 1．图形中的周期问题；2．数列中的周期问题；3．年月日中的周期问题．周期性问题的基本解题思路是：首先要正确理解题意，从中找准变化的规律，利用这些规律作为解题的依据；其次要确定解题的突破口。

主要方法有观察法、逆推法、经验法等。

主要问题有年月日、星期几问题等。

⑴观察、逆推等方法找规律，找出周期．确定周期后，用总量除以周期，如果正好有整数个周期，结果就为周期里的最后一个；例如：1，2，1，2，1，2，…那么第18个数是多少？这个数列的周期是2，，所以第18个数是2．1829÷=⑵如果比整数个周期多个，那么为下个周期里的第个；n n 例如：1，2，3，1，2，3，1，2，3，…那么第16个数是多少？这个数列的周期是3，，所以第16个数是1．16351÷=⋅⋅⋅⑶如果不是从第一个开始循环，可以从总量里减掉不是循环的个数后，再继续算．例如：1，2，3，2，3，2，3，…那么第16个数是多少？这个数列从第二个数开始循环，周期是2，，所以第16(161)271-÷=⋅⋅⋅个数是2．二、图形中的周期问题例1：小兔和小松鼠做游戏，他们把黑、白两色小球按下面的规律排列：●●○●●○●●○…你知道它们所排列的这些小球中，第90个是什么球？第100个又是什么球呢？例2：美美有黑珠、白珠共102个，她想把它们做成一个链子挂在自己的床头上，她是按下面的顺序排列的：○●○○○●○○○●○○○……那么你知道这串珠子中，最后一个珠子应是什么颜色吗？美美怕白颜色的珠子数量不够，你能帮她算出这种颜色在这串珠子中有多少个吗？练一练：1.小倩有一串彩色珠子，按红、黄、蓝、绿、白五种颜色排列．⑴第73颗是什么颜色的？⑵第10颗黄珠子是从头起第几颗？⑶第8颗红珠子与第11颗红珠子之间（不包括这两颗红珠子）共有几颗珠子？2. 奥运会就要到了，京京特意做了一些“北京欢迎你”的条幅，这些条幅连起来就成了：“北京欢迎你北京欢迎你北京欢迎你……”依次排列，第28个字是什么字？3. 节日的校园内挂起了一盏盏小电灯，小明看出每两个白灯之间有红、黄、绿各一盏彩灯．也就是说，从第一盏白灯起，每一盏白灯后面都紧接着有3盏彩灯．那么第73盏灯是什么颜色的灯？4. 节日的夜景真漂亮，街上的彩灯按照5盏红灯、再接4盏蓝灯、再接1盏黄灯，然后　又是5盏红灯、4盏蓝灯、1盏黄灯、……这样排下去．问：⑴第150盏灯是什么颜色？⑵前200盏彩灯中有多少盏蓝灯？5.在一根绳子上依次穿2个红珠、2个白珠、5个黑珠，并按此方式反复，如果从头开始数，直到第50颗，那么其中白珠有多少颗？6.如图所示，每列上、下两个字（字母）组成一组，例如，第一组是“我，”，A第二组是“们，”……B我们爱科学我们爱科学我……A B C D E F G A B C D……⑴写出第62组是什么？⑵如果“爱，”代表1991年，那么“科，”代表1992年……问2008C D年对应怎样的组？7.在图所示的表中，将每列上、下两个字组成一组，例如第一组为（新奥），第二组为（北林），那么第50组是什么？新北京新奥运新北京新奥运新北京新奥运……奥林匹克运动会奥林匹克运动会奥林匹克运动会……8.如右图，是一片刚刚收割过的稻田，每个小正方形的边长是1米，A、B、C 三点周围的阴影部分是圆形的水洼。

第三十七章周期问题概念一、周期问题1．周期现象事物在运动变化过程中，某些特征有规律循环出现；周期：我们把连续两次出现所经过的时间叫周期；解决有关周期性问题的关键是确定循环周期.分类： 1．图形中的周期问题；2．数列中的周期问题；3．年月日中的周期问题．2．周期性问题的基本解题思路是首先要正确理解题意，从中找准变化的规律，利用这些规律作为解题的依据；其次要确定解题的突破口。

主要方法有观察法、逆推法、经验法等。

主要问题有年月日、星期几问题等。

⑴观察、逆推等方法找规律，找出周期．确定周期后，用总量除以周期，如果正好有整数个周期，结果就为周期里的最后一个；例如：1，2，1，2，1，2，…那么第18个数是多少？这个数列的周期是2，1829÷=，所以第18个数是2．⑵如果比整数个周期多n个，那么为下个周期里的第n个；例如：1，2，3，1，2，3，1，2，3，…那么第16个数是多少？这个数列的周期是3，16351÷=⋅⋅⋅，所以第16个数是1．⑶如果不是从第一个开始循环，可以从总量里减掉不是循环的个数后，再继续算．例如：1，2，3，2，3，2，3，…那么第16个数是多少？这个数列从第二个数开始循环，周期是2，(161)271-÷=⋅⋅⋅，所以第16个数是2例题1. 小兔和小松鼠做游戏，他们把黑、白两色小球按下面的规律排列：●●○●●○●●○…你知道它们所排列的这些小球中，第90个是什么球？第100个又是什么球呢？2. 美美有黑珠、白珠共102个，她想把它们做成一个链子挂在自己的床头上，她是按下面的顺序排列的：○●○○○●○○○●○○○……那么你知道这串珠子中，最后一个珠子应是什么颜色吗？美美怕这种颜色的珠子数量不够，你能帮她算出这种颜色在这串珠子中共有多少个吗？3.小倩有一串彩色珠子，按红、黄、蓝、绿、白五种颜色排列．⑴第73颗是什么颜色的？⑵第10颗黄珠子是从头起第几颗？⑶第8颗红珠子与第11颗红珠子之间（不包括这两颗红珠子）共有几颗珠子？4. 奥运会就要到了，京京特意做了一些“北京欢迎你”的条幅，这些条幅连起来就成了：“北京欢迎你北京欢迎你北京欢迎你……”依次排列，第28个字是什么字？5. 节日的校园内挂起了一盏盏小电灯，小明看出每两个白灯之间有红、黄、绿各一盏彩灯．也就是说，从第一盏白灯起，每一盏白灯后面都紧接着有3盏彩灯．那么第73盏灯是什么颜色的灯？6. 节日的夜景真漂亮，街上的彩灯按照5盏红灯、再接4盏蓝灯、再接1盏黄灯，然后又是5盏红灯、4盏蓝灯、1盏黄灯、……这样排下去．问：⑴第150盏灯是什么颜色？⑵前200盏彩灯中有多少盏蓝灯？7. 在一根绳子上依次穿2个红珠、2个白珠、5个黑珠，并按此方式反复，如果从头开始数，直到第50颗，那么其中白珠有多少颗？8. 小莉把平时积存下来的200枚硬币按3个1分，2个2分，1个5分的顺序排列起来．⑴最后1枚是几分硬币⑵这200枚硬币一共价值多少钱？9. 桌子上摆了很多硬币，按一个一角，两个五角，三个一元的次序排列，一共19枚硬币．问：最后一个是多少钱的？第十四个是多少钱的？10. 有249朵花，按5朵红花，9朵黄花，13朵绿花的顺序轮流排列，最后一朵是什么颜色的花？这249朵花中，什么花最多，什么花最少？最少的花比最多的花少几朵？11. 如图所示，每列上、下两个字（字母）组成一组，例如，第一组是“我，A⑴写出第62组是什么？⑵如果“爱，C”代表1991年，那么“科，D”代表1992年……问2008年对应怎样的组？12. 在图所示的表中，将每列上、下两个字组成一组，例如第一组为（新奥），第二组为（北林），那么第50组是什么？13. 如右图，是一片刚刚收割过的稻田，每个小正方形的边长是1米，A、B、C三点周围的阴影部分是圆形的水洼。

【例题】：2001年10月1日是星期一，10月25日是星期几？【例题精讲】：我们知道，每个星期有7天，也就是说以7天为一个周期不断地重复。

10月1日是星期一，那么再过7天，就是8号，还是星期一。

所以要求10月25日是星期几，首先要求出10月1日到10月25日一共多少天（包括10月1日），那么从10月1日到10月25日经过了25天。

25天中包括了3个星期还多4天，因此用除法算式解答。

（1）从10月1日到10月25日有：25天。

（2）25天里有多少个星期余多少天？25÷7=3（个星期）……4（天）。

（说明25天中包含3个星期还多4天，这个多的四天，是每个周期的第四天，也就是星期四。

）答：10月25日是星期四。

首先找到题目当中多少个为一个循环的周期，然后用除法来进行解答，然后看余数，余数是几，就是这个规律中的第几个。

【同步练习】1. 今天是星期日，再过38天是星期几？2. 2001年6月1日是星期五，9月1日是星期几？3. 2002年元旦是星期二，那么，2003年1月1日是星期几？【例题】国庆节挂彩灯，按“红、黄、蓝、白、绿、紫”的顺序挂，一共挂了50只彩灯，第50只彩灯是什么颜色的？红色的彩灯一共有多少只？【例题精讲】由题意可知，这些彩灯按“红、黄、蓝、白、绿、紫”六种颜色的顺序六种为一周期循环。

因50÷6=8（组）……2（只），所以第50只彩灯的颜色与第二只彩灯的颜色相同。

第8个周期后又挂出的两盏彩灯是红色和黄色的，所以红色彩灯共有8+1=9（只）。

50÷6=8(组)……2（只），8+1=9（只）。

答：第50只彩灯是黄色的，红色的彩灯一共有9只。

在用用周期问题的方法找到规律以后，再进一步算出题中每个量各是多少。

这是周期问题的进一步运用。

【同步练习】1. 有同样大小的红、白、黑球共120个，按先3个红的，后2个白的，再1个黑的排列，问：（1）白球一共有多少个？（2）第68个球是什么颜色？2. 一本童话书，每两页文字之间有3页插图，也就是说3页插图前后各有1页文字，如果这本书有128页，而第1页是文字，这本书共有插图多少页？3. 小军数左手的手指，大拇指为1，食指为2，中指为3，无名指为4，小指为5，然后换方向再数，无名指为6，中指为7，食指为8，大拇指为9，再换方向书，食指为10，……这样数到2006，停在哪个手指上？。

第六讲周期问题一、知识要点和基本方法1．周期问题客观世界中，存在着一些数、图形和事物的变化是周而复始循环出现的，我们把具有这种规律性的问题称为周期问题．例如，每隔7天是一周，周周如此；每隔12个月是一年，年年一样；每隔24小时是一昼夜，天天相同；……，这些问题都属于周期问题．2．周期问题中的周期周期是一个数，由于我们所学的知识有限，还不能给出周期的明确定义，只能具体问题具体分析．例如，由于每个星期有7天，即时间是7天一循环，则说周期是7；由于每年有12个月，即时间是12个月一循环测说周期是12；每个昼夜24个小时，即时间是24个小时一循环，则说周期是24；在循环小数中，“循环节数字的位数”即为循环的“周期”．研究周期问题，就是要发现问题的周期性和确定周期，从而解决有关问题．3．利用余数处理离散序列周期性问题的一般模式．余数反映了自然数的某种周期变化。

它可以帮助我们确定具有周期规律的离散量在某个序号上的性质．解决这种问题的一般模式是：（1）序列：123456789···,a a a a a a a a a ，，，，，，，，，↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓性质： 123451234···P P P P P P P P P ，，，，，，，，，． 其中，12345p p p p p ，，，，是以5为周期循环的数字12a a ，，…所对应的性质．（2）若问k a 对应什么性质？我们只要用5去除k ，看余数是几就可以了．比如1998a ，因为1998 ÷ 5=399……3，立即可判定1998a 具有性质3p ．4．自然数乘方的个位数所呈现的周期现象．一个数码a 自乘后，积的个位数是有周期现象的，我们把数码a 自乘m 次后记作=m m a a a a a ⨯⨯⨯⋅⋅⋅⨯个，记作a 的m 次方则易知数码0，1，5，6的任何次方的个位数仍是它本身．数码2，3，4，7，8，9的m 次方的个位数有如下周期现象。

周期问题练习题周期问题练习题周期是自然界中普遍存在的一种现象。

从昼夜交替、月相变化到季节更迭，周期性的变化无处不在。

周期问题是数学中的一个重要概念，它不仅在数学中有广泛的应用，也贯穿于生活的方方面面。

本文将通过一系列练习题，帮助读者更好地理解和应用周期问题。

1. 假设一辆车以每小时60公里的速度匀速行驶，那么这辆车每隔多长时间会行驶100公里？解析：根据速度等于路程除以时间的公式，我们可以得到时间等于路程除以速度。

所以，这辆车行驶100公里所需的时间为100/60 = 5/3小时。

换算成分钟，即5/3 * 60 = 100分钟。

因此，这辆车每隔100分钟会行驶100公里。

2. 一只蜜蜂每分钟跳动150次翅膀，那么它每小时跳动多少次翅膀？解析：根据时间与频率的关系，我们知道频率等于次数除以时间。

所以，这只蜜蜂每分钟跳动150次翅膀，那么它每小时跳动的次数为150 * 60 = 9000次翅膀。

3. 一台机器每隔3秒钟发出一次“滴答”声，那么它每小时发出多少次“滴答”声？解析：将时间单位统一为秒，这台机器每隔3秒钟发出一次“滴答”声，那么它每小时发出的次数为3600/3 = 1200次“滴答”声。

4. 一盏灯每隔5分钟闪烁一次，那么在两个小时内它会闪烁多少次？解析：将时间单位统一为分钟，这盏灯每隔5分钟闪烁一次，那么在两个小时内它会闪烁的次数为2 * 60 / 5 = 24次。

5. 一只青蛙每隔30秒跳跃一次，那么在一小时内它会跳跃多少次？解析：将时间单位统一为秒，这只青蛙每隔30秒跳跃一次，那么在一小时内它会跳跃的次数为3600/30 = 120次。

通过以上练习题，我们可以看到周期问题在日常生活中的广泛应用。

从车辆行驶，到生物活动，都存在着一定的周期性变化。

对于数学而言，周期问题是一个重要的研究领域，它涉及到函数、图像和方程等多个数学概念的应用。

周期问题的研究不仅帮助我们更好地理解和描述自然界的现象，还有助于解决实际问题。

第10讲周期问题【探究必备】每周有7天，从周一到周日，周而复始地出现，每年有12个月，从1月到12月周而复始地出现，每年有4季，从春天到冬天，周而复始地出现，……，在日常生活和学习中，人们把这种有规律的重复出现的现象叫做周期现象，把有规律的重复出现的一个单位称为周期，例如周一到周日称作一个周期，这个周期为7，从1月到12月称作一个周期，这个周期为12，……。

解决周期问题的关键是找准周期和总数，然后用“总数÷周期”，根据余数来解决问题，如果没有余数，该物体（颜色）就是这个周期的最后一个，如果有余数，该物体（颜色）就从这个周期的第一个数起，余数是几就数几个。

解决较复杂的周期问题，找准周期是难点。

有时采用写一写、列表、画图等方式，对发现并找准周期有很大的帮助。

【王牌例题】例1、有一些黑球与白球，排成如下图形状：○○●○○●○○●○……第24个什么颜色的球？第50个呢？分析与解答：从图上我们不难发现，排列的规律是2白1黑（○○●），周期是3。

再看24、50里面包含有几个这样的周期（组），若正好有整数个周期（组），结果为该周期里的最后一个，如24÷3=8（组），则第24个为黑球；若是几个周期余几个，结果为下一个周期里的第几个，如50÷3=16（组）……2（个），则第50个为第17个周期里的第2个，即白球。

例2、有一些黑球与白球，排成如下图形状：○●○○●○○●○○●○……前40个球里面有多少个黑球？有多少个白球？分析与解答：这些球排列是有规律的，即1白1黑1白，把这看作一个周期（组），首先计算出前40个球按1白1黑1白的规律排成几个周期还剩几个，剩的几个分别是什么颜色的球，即40÷3=13（组）……1（个），分13组余1个（白球），因为一个周期里面有2个白球和1个黑球，所以13个周期里共有黑球1×13=13（个），白球2×13+1=27（个）。

例3、一次数学课上，陈老师在黑板上写下一组数：3、5、2、0、8、3、5、2、0、8、3、5、2、0、8……问：同学们，你们能很快求出前81个数的和吗？ 分析与解答：因为这些数都是按3、5、2、0、8排列的，可以把它们看作一个周期（组），周期为5，首先算出前80个数有几个周期，还余下几个，即81÷5=16（组）……1（个），可以分成16个周期还剩1个，数字为3，因为一个周期的和为3+5+2+0+8=18，则前81个数的和为18×16+3=291。

周期问题之巧算星期几
例1、某年的10月2日是星期二，那么，22天后是星期几？
练习1：某年的3月1日是星期四，那么，26天后是星期几？
练习2：某年的6月6日是星期天，那么，18天后是星期几？
练习3：2011年的7月5日是星期二，那么，6天后是星期几？16天后是星期几？
例2：2011年的7月1日是星期五，那么，7月26日是星期几？7月30日是星期几？
练习4: 2011年的六一儿童节是星期三，那么，6月18日是星期几？6月22日呢？
练习5: 2010年的教师节是星期五，那么，9月20日是星期几？9月29日呢？
练习6：某一年的1月1日是星期三，那么，1月8日是星期几？1月20日呢？1月30日呢？
例3：一年中的1月、2月、3月、4月、5月、6月、7月、8月、9月、10月、11月、12月分别有多少天？
例4：2010年的9月10日是星期五，那么，2010年的10月5日是星期几？11月2日呢？12月18日呢？
练习7: 2011年7月22日是星期五，那么，这个月的31日是星期几？2011年的8月8日是星期几？9月21日呢？10月30日呢？
练习8: 2010年的3月22日是星期一，那么，这个月的3月30日是星期几？5月12日呢？6月22日呢？7月14日呢？10月11日呢？12月30日呢？。

周期问题知识点总结周期问题是指周期性发生并且可以被预测的事件或现象。

它们在自然界和人类生活中随处可见，涵盖了从微观到宏观的各种领域。

周期问题的研究不仅有助于我们更好地理解自然规律和社会现象，还为我们提供了有效的预测和管理周期性事件的工具。

本文将从周期问题的定义、分类、原因以及周期问题的应用等方面进行总结。

一、周期问题的定义周期问题是指某一事件或现象在一定时间内出现相同或相似的情况，形成一定的规律性。

周期问题是自然界和社会生活中常见的一种现象，如地球公转、季节更替、人类的生物钟等都属于周期问题。

周期问题可分为固定周期和不固定周期两种。

固定周期是指在一定的时间内，事件或现象重复出现的间隔是固定的，如地球自转一周为一个固定周期。

不固定周期是指在一定的时间内，事件或现象重复出现的间隔不是固定的，如人类的月经周期就是一个不固定周期。

二、周期问题的分类周期问题可以根据其发生的规律性、周期性和性质进行分类。

根据发生的规律性，周期问题可以分为简单周期问题和复杂周期问题两种。

简单周期问题是指事件或现象在一定时间内规律性地重复出现，如月相变化、潮汐运动等都属于简单周期问题。

复杂周期问题是指在一定时间内，事件或现象具有多重规律性，常常呈现多个周期共存的情况，如气候变化、人口增长等都属于复杂周期问题。

根据周期性，周期问题可以分为长周期问题和短周期问题两种。

长周期问题是指事件或现象在较长的时间内重复出现，如地球的气候变化、人类的历史发展等都属于长周期问题。

短周期问题是指事件或现象在较短的时间内规律性地重复出现，如月相变化、潮汐运动等都属于短周期问题。

三、周期问题的原因周期问题的形成有多种原因，主要包括自然原因和社会原因。

自然原因是指事件或现象周期性发生的原因是由于自然界规律性的变化引起的，如地球的公转、月球的绕地运动等都是自然原因引起的周期问题。

社会原因是指事件或现象周期性发生的原因是由于社会经济、文化、政治等因素引起的，如经济周期、社会风气变化等都是社会原因引起的周期问题。