大学物理-质心
- 格式:pptx
- 大小:152.67 KB
- 文档页数:21









大学物理力学第六章质心运动定理(二)引言概述:大学物理力学的第六章质心运动定理(二)是质点系的动力学描述的重要内容。
本文将从引入质心的概念开始,逐步介绍质心运动定理的原理和应用。
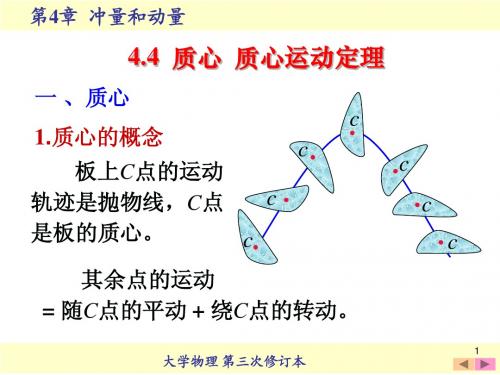
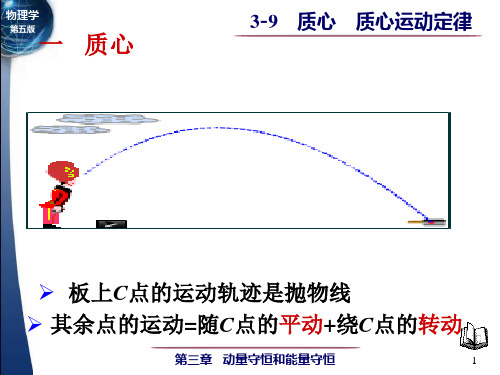
正文:1. 质心的定义和性质:- 质心被定义为质点系中所有质点质量加权平均位置的矢量。
- 质心具有质点系中所有质点质量的总和,并且在质点系运动中保持位置不变。
- 质心的运动可以简化质点系的运动分析。
2. 质心运动定理的表述:- 质心运动定理指出,在外力作用下,质心的加速度等于质点系所受合外力与质点系总质量的比例。
- 质心的加速度可以通过所有质点受力的合力除以质点系总质量得到。
3. 质心运动定理的证明和推导:- 通过应用牛顿第二定律,可以推导出质心运动定理的表达式。
- 使用质点系质量的定义、质心的定义以及质点系中每个质点的位矢,可以推导出质心关于时间的二阶导数与质点系合外力的关系式。
4. 质心运动定理的应用:- 可以通过质心运动定理计算质心在不同外力作用下的加速度。
- 质心运动定理可以用于解决质点系的多体动力学问题。
- 质心运动定理对于研究刚体的运动也具有重要意义。
5. 质心运动定理的限制和扩展:- 质心运动定理只适用于质点系在外力作用下的运动,不适用于内力相互作用的情况。
- 在非惯性系中,质心运动定理需要进行修正。
- 质心运动定理可以扩展应用于连续体力学的问题分析。
总结:大学物理力学第六章质心运动定理(二)介绍了质心的概念和性质,阐述了质心运动定理的原理和推导过程,并探讨了质心运动定理的应用范围和限制。
掌握质心运动定理对于解决质点系的动力学问题非常重要,并且在刚体和连续体力学领域也有广泛应用。



第二章 运动的守恒量和守恒定律练 习 一一. 选择题1。
关于质心,有以下几种说法,你认为正确的应该是( C )(A ) 质心与重心总是重合的; (B ) 任何物体的质心都在该物体内部; (C ) 物体一定有质心,但不一定有重心; (D ) 质心是质量集中之处,质心处一定有质量分布。
2。
任何一个质点系,其质心的运动只决定于( D )(A )该质点系所受到的内力和外力; (B ) 该质点系所受到的外力;(C ) 该质点系所受到的内力及初始条件; (D ) 该质点系所受到的外力及初始条件。
3。
从一个质量均匀分布的半径为R 的圆盘中挖出一个半径为2R 的小圆盘,两圆盘中心的距离恰好也为2R 。
如以两圆盘中心的连线为x 轴,以大圆盘中心为坐标原点,则该圆盘质心位置的x 坐标应为( B ) (A )R 4; (B) R 6; (C ) R 8; (D R12。
4. 质量为10 kg 的物体,开始的速度为2m/s ,由于受到外力作用,经一段时间后速度变为6 m/s,而且方向转过90度,则该物体在此段时间内受到的冲量大小为 ( B )(A )s N ⋅820; (B) s N ⋅1020; (C ) s N ⋅620; (D) s N ⋅520。
二、 填空题1. 有一人造地球卫星,质量为m ,在地球表面上空2倍于地球半径R 的高度沿圆轨道运行,用m 、R 、引力常数G 和地球的质量M 表示,则卫星的动量大小为RGM m3。
2.三艘质量相等的小船在水平湖面上鱼贯而行,速度均等于0v ,如果从中间小船上同时以相对于地球的速度v 将两个质量均为m 的物体分别抛到前后两船上,设速度v 和0v 的方向在同一直线上,问中间小船在抛出物体前后的速度大小有什么变化:大小不变。
3. 如图1所示,两块并排的木块A 和B ,质量分别为m 1和m 2,静止地放在光滑的水平面上,一子弹水平地穿过两木块。
设子弹穿过两木块所用的时间分别为∆t 1和∆t 2,木块对子弹的阻力为恒力F ,则子弹穿出后,木块A 的速度大小为 1A BF t m m ⋅∆+,木块B 的速度大小为12F t A BBF t m m m ⋅∆⋅∆++.三、计算题1. 一质量为m 、半径为R 的薄半圆盘,设质量均匀分布,试求薄半圆盘的质心位置。

大学物理力学 怎么求解质心位置清华大学电子工程系 无13班 蔡杨原理:利用的是质心的性质。
对于一个质点系,质心可以代表这个质 点系的受力情况。
当然这对于重力也就成立。
因此理论上,任意一个 平面物体悬挂后,质心都应该位于悬线所在的直线上 (这条直线也是 重力对于物体的作用线) 二. 定义法(1)对于多质点系统:(2)对于质量分布连续的物体:可以写出三个分量式mj im irni i X im im i ym im i 召mirX cy cZ c三. 对称法 对于一个质量分布均匀的物体,其质心位于其几何中心。
因此,轴对 称图形的质心位于其对称轴上(几何中心位于对称轴上)四. 组合法 对于由好几部分质量已知且质心位置已知的质点系组成的系统: 质量:叶(质点系1),m 2(质点系2),m 3(质点系3),…,m (质点系i ),… 位置:r 1(质点系1), r 2(质点系2), r 3(质点系3),…,r i (质点系i ),'整个系统的质心位置仍由下式决定:例如:一个质点m (位置为r 1)和一个刚体M (其质心位置为r ;)组可以写出三个分量式r cXcy cJ(PdV)r i J PdVf rdV)x iJ PdV J(PdV)y iJ PdV【(PdV )乙J PdVrc艺mj i 送m i成的系统的质心的位置为:f '面密度为(。
的圆盘的叠加。
则由方法四,不难得出:M 1r 1 十 M 2r 2沪 cR )2]2R 2珥兀 R )+(〜)!(一)]6R?此即其质心的位置 *六.巴普斯定理五.负质量法-mr^ Mr 2 rc =m+ M此方法用于求解:规则图形挖去一部分的图形求 心的问题。
如:下图为一半径为R 的均匀圆盘,挖去 一个半径为2的圆形部分。
试求其 质心所在的位置。
解答:如图建立坐标。
有对称性,质心必定 于x 轴上。
假设该图形为一个半径为R ,面密度为b 的圆盘和一个半径为解质位这个定理在微积分的课上曾经有所涉及。


大学物理中引入质心的作用作者:郑晓毅来源:《文理导航·教育研究与实践》2015年第07期【摘要】质心概念是大学物理中一个重要的知识点,有着非常广泛的应用。
文章从质心的引入和定义出发,分析了质心概念在多体系统的动量守恒定理、刚体力学中的平行轴定理、刚体的动能与势能中的重要应用。
表明引入质心概念在处理经典物理问题的优越性。
【关键词】质心;动量守恒;平行轴定理;平动动能;转动动能中图分类号:O412 文献标识码:A 文章编号:在大学物理中,质心是质点系力学和刚体力学中一个非常重要的概念,而且应用广泛。
诸如多体系统的动量守恒定理,刚体力学中的平行轴定理,刚体的动能与势能推导中都可以看到质心的作用。
这些物理定理的掌握与应用,是学生在大学物理课程学习的重要内容。
本文从质心的引入以及定义出发,从几个方面分析了质心概念在大学物理中的重要应用。
一、质心的引入:考虑最简单的一维空间中的两个物体1和2,质量分别为m1和m2。
讨论两个物体的动力学方程,应用牛顿第二定律,对于物体1,有:m1=m1x1=F1=F21+F1e ; ; (1)其中x1为的简写,F12表示物体2对物体1的作用力,Fle表示除物体2以外外界对物体1的作用力,F1便表示物体1所受到的合外力。
同理,对于物体2,有:m2=m2x2=F2=F12+F2e ; ; (2)将式(1)和式(2)左右两边相加起来,则有:m1x1+m2x2=F12+F1e+F21+F2e ; ;(3)根据牛顿第三定律,式(3)可以简化为:m1x1+m2x2=F1e+F2e+Fe ; ; (4)此时,我们引入一个新的物理量,令其为:X=,式(4)则可改写成:MX=Fe引入的新物理量则为质心,它是系统质量分布位置的一种加权平均,表明对于整个系统,可以将其看成是所有质量位于质心处的一个整体,其动力学方程仅受到合外力的影响,这便是质心以及质心运动定理。
将以上质心的概念推广到多维空间中多个物体构成的质点系,得到质心的一般形式:M=e,其中=,M=mi,其中,二、质心与多体系统的动量守恒定理对于质点系组成的多体系统,其动力学规律满足质心运动定理。
