大学物理 质心

质心公式的推导摘要：1.质心定义及作用2.质心公式推导过程3.质心公式应用实例4.质心在实际生活中的重要性正文：质心，又称重心，是一个物体在空间中的平衡点。

它在物理学、力学等领域具有重要的理论价值和实践意义。

本文将介绍质心公式的推导过程，并举例说明其在实际生活中的应用。

一、质心定义及作用质心是一个物体所有部分的质量均匀分布时，物体内部各个部分所受重力的合力作用点。

在二维平面内，质心位于物体形心的位置。

质心在物体平衡、稳定以及运动过程中的作用至关重要。

它可以帮助我们分析物体在各种受力情况下的运动状态，为工程设计、建筑结构等领域提供理论依据。

二、质心公式推导过程质心公式是根据物体的质量分布和形状来计算质心位置的。

设物体质量为m，物体形状为S，物体上的任意一点到质心的距离为r。

根据物体质量分布的均匀性，可以得到以下公式：质心位置（x，y）= （Σmr / Σm）/ S其中，Σmr表示物体各部分质量与质心距离的乘积之和，Σm表示物体各部分质量之和。

通过数学运算，我们可以得到质心的坐标。

三、质心公式应用实例1.简单几何体：对于简单的几何体，如长方体、圆柱体等，可以通过测量各部分的尺寸和质量，直接计算出质心位置。

2.复杂物体：对于复杂的物体，如飞机、汽车等，需要先将物体分解为简单的几何体，然后分别计算各部分的质心，最后通过一定的算法求得整个物体的质心。

3.建筑结构：在建筑结构设计中，了解结构的质心位置有助于分析结构的稳定性和抗风能力。

通过计算质心，可以合理布局建筑物的重量分布，提高建筑物的抗风性能。

四、质心在实际生活中的重要性1.平衡控制：在运动控制、机器人等领域，掌握质心位置对于保持物体平衡具有重要意义。

例如，在无人驾驶汽车中，通过实时监测质心位置，可以有效避免因质心偏移导致的失控现象。

2.优化设计：在产品设计和工程设计中，合理调整质心位置可以提高产品的性能和稳定性。

例如，在飞机设计中，通过改变机翼形状和位置，可以调整质心与飞行速度的关系，实现更高效的飞行。

质心知识点总结归纳质心（Center of Mass）是物体集中质量的平均位置。

在物理学中，质心是描述物体运动的重要概念，对于研究物体的运动、碰撞、转动等现象都有重要的意义。

同时，质心在工程、航天航空等领域也有着广泛的应用。

质心的计算方法有多种，可以通过物体的密度分布、几何形状和其他条件来进行计算。

而质心的运动规律也可以通过牛顿定律和动量定律来描述。

本文将从质心的概念、计算方法、运动规律以及工程应用等方面对质心的知识点进行总结和归纳。

一、质心的概念1. 定义质心是物体所有质点的集中位置，也可以看作是物体的平衡点。

在质心系中，物体的总动量和总角动量相对于质心系均为零。

2. 特点（1）质心不一定位于物体内部，可以位于物体的外部；（2）质心的运动不一定与物体的其他点相同；（3）质心的位置与物体的形状和质量分布有关；（4）质心具有跟随物体运动的特点。

二、质心的计算方法1. 特殊形状物体的质心计算（1）均匀杆对于一根均匀杆，质心位于杆的中点处。

（2）均匀圆环对于一个均匀圆环，质心位于环的中心处。

2. 连续体的质心计算对于连续分布的质量分布，可以通过积分的方法来计算质心。

一般来说可以使用以下公式来计算：\[ x_{cm} = \frac{1}{M} \int x\;dm \]\[ y_{cm} = \frac{1}{M} \int y\;dm \]\[ z_{cm} = \frac{1}{M} \int z\;dm \]其中，\( x_{cm} \)、\( y_{cm} \)、\( z_{cm} \) 分别表示质心在 x、y、z 方向上的位置，M 表示物体的总质量。

三、质心的运动规律1. 质心的运动状态质心的运动状态可以通过牛顿定律和动量定律描述。

在外力作用下，质心会产生加速度，并且质心的加速度与物体的质量成反比。

2. 刚体的平动运动对于刚体的平动运动，可以通过质心的运动来描述整个刚体的运动状态。

刚体的平动运动可以看作是质心的平动运动。

大学物理力学第六章质心运动定理（二）引言概述：大学物理力学的第六章质心运动定理（二）是质点系的动力学描述的重要内容。

本文将从引入质心的概念开始，逐步介绍质心运动定理的原理和应用。

正文：1. 质心的定义和性质：- 质心被定义为质点系中所有质点质量加权平均位置的矢量。

- 质心具有质点系中所有质点质量的总和，并且在质点系运动中保持位置不变。

- 质心的运动可以简化质点系的运动分析。

2. 质心运动定理的表述：- 质心运动定理指出，在外力作用下，质心的加速度等于质点系所受合外力与质点系总质量的比例。

- 质心的加速度可以通过所有质点受力的合力除以质点系总质量得到。

3. 质心运动定理的证明和推导：- 通过应用牛顿第二定律，可以推导出质心运动定理的表达式。

- 使用质点系质量的定义、质心的定义以及质点系中每个质点的位矢，可以推导出质心关于时间的二阶导数与质点系合外力的关系式。

4. 质心运动定理的应用：- 可以通过质心运动定理计算质心在不同外力作用下的加速度。

- 质心运动定理可以用于解决质点系的多体动力学问题。

- 质心运动定理对于研究刚体的运动也具有重要意义。

5. 质心运动定理的限制和扩展：- 质心运动定理只适用于质点系在外力作用下的运动，不适用于内力相互作用的情况。

- 在非惯性系中，质心运动定理需要进行修正。

- 质心运动定理可以扩展应用于连续体力学的问题分析。

总结：大学物理力学第六章质心运动定理（二）介绍了质心的概念和性质，阐述了质心运动定理的原理和推导过程，并探讨了质心运动定理的应用范围和限制。

掌握质心运动定理对于解决质点系的动力学问题非常重要，并且在刚体和连续体力学领域也有广泛应用。

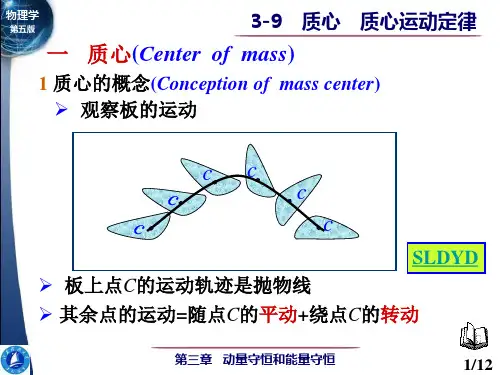
力学中的质心力学中的质心（Center of Mass in Mechanics）在力学中，质心（Center of Mass）是一个经常被讨论的主题。

质心是一个物体的几何中心，它可以用来描述物体在力学中的运动和平衡。

本文将深入探讨质心的概念、计算方法以及其在力学中的应用。

一、质心的定义和特性质心被定义为一个物体的总质量分布在空间中的几何中心。

对于一个质点系统或一个具有连续分布的物体，质心是一个特殊的点，它具有以下特性：1. 质心的位置与物体的形状和质量分布有关。

当物体具有对称性时，质心通常位于物体中心或中轴线上。

但对于不规则形状的物体，质心的位置可能会有所偏移。

2. 质心是一个虚拟的点，它不一定处于物体实际存在的位置。

即使一个物体是孔洞或空洞的，它的质心也可以在物体的实际存在之外。

3. 对于一个质点系统或一个连续分布的物体，质心的位置可以通过对质量进行加权平均来计算。

质心的坐标可以用矢量的形式表示。

二、质心的计算方法计算质心的位置需要考虑物体的质量和质量分布。

有几种常见的方法可以计算质心的坐标。

1. 对于一个质点系统，可以通过将每个质点的质量与其位置的乘积相加，再除以总质量来计算质心的位置。

这可以表示为：x_cm = (m1x1 + m2x2 + ... + mnxn) / (m1 + m2 + ... + mn)y_cm = (m1y1 + m2y2 + ... + mnyn) / (m1 + m2 + ... + mn)z_cm = (m1z1 + m2z2 + ... + mnzn) / (m1 + m2 + ... + mn)其中，m是质量，x、y和z是位置坐标。

2. 对于一个连续分布的物体，可以使用积分来计算质心的位置。

假设物体沿着x轴分布，可以表示为：x_cm = ∫x dm / ∫dm同样，可以使用相同的方法计算y和z方向的质心坐标。

三、质心在力学中的应用质心在力学中有着广泛的应用，特别是在描述物体的运动和平衡时。

质心运动质心如何影响物体的整体运动质心运动：质心如何影响物体的整体运动质心是物体的一个特殊点，可以用来描述物体的整体运动状态。

在物理学中，质心运动和质心的性质十分重要，对于研究物体的运动具有重要意义。

本文将重点介绍质心运动的概念和质心如何影响物体的整体运动。

1. 质心的定义和计算方法质心是物体的一个点，它具有以下性质：- 质心位于物体的对称轴上；- 物体上所有点到质心的距离乘以质点的质量之和等于零；- 质心是物体的一个固定点，无论物体如何变形或移动，质心的位置不变。

计算质心的方法取决于物体的形状和密度分布。

对于均匀密度的物体，质心位于物体的几何中心。

而对于不均匀密度的物体，可以利用积分来计算质心的位置。

2. 质心运动的概念质心运动是指质心随着时间的推移而移动的过程。

当物体受到外力或外力矩的作用时，质心会随着外力的作用而产生加速度，从而改变其位置和速度。

根据牛顿第二定律，物体的加速度与作用在该物体上的合外力成正比，质心也不例外。

质心的加速度可以通过下面的公式计算：F = ma其中F是物体受到的合外力，m是物体的质量，a是质心的加速度。

3. 质心的影响质心的运动对物体的整体运动有着重要的影响。

以下是质心运动对物体整体运动的几个具体影响：3.1 保持平衡：当物体受到外力作用时，质心会产生加速度，但物体的整体运动状态仍然保持平衡。

这是因为物体上所有点的加速度都与质心的加速度相同，质心运动不会导致物体发生旋转或倾斜。

3.2 简化分析：通过研究质心的运动，可以简化对物体运动的分析。

可以将物体的复杂运动分解为质心的平动运动和围绕质心的自转运动两个部分，分别研究它们的运动规律。

3.3 确定力的合力点：质心的位置可以用来确定物体受力的合力点。

当物体受到多个力的作用时，可以通过计算质心位置来确定合力点的位置，从而进一步分析物体的受力情况。

3.4 影响整体运动轨迹：质心的运动轨迹决定了物体的整体运动轨迹。

当质心的运动轨迹为一条直线时，物体的整体运动是直线运动。

质心mass，centre of质量中心或称质心，指物质系统上被认为质量集中于此的一个假想点。

与重心不同的是，质心不一定要在有重力场的系统中。

值得注意的是，除非重力场是均匀的，否则同一物质系统的质心与重心不通常在同一假想点上。

在一个N维空间中的质量中心，坐标系计算公式为：X表示某一坐标轴mi 表示物质系统中，某i质点的质量xi 表示物质系统中，某i质点的坐标。

质点系质量分布的平均位置。

质量中心的简称。

它同作用于质点系上的力系无关。

设n个质点组成的质点系，其各质点的质量分别为m1，m2，…，mn。

若用r1 ，r2，…，rn分别表示质点系中各质点相对某固定点的矢径，rc 表示质心的矢径，则有rc＝Image:质心１.jpgmiri ／Image:质心１.jpgmi。

当物体具有连续分布的质量时，质心C的矢径rc＝Image:质心２.jpgρrdτ／Image:质心２.jpgρdτ，式中ρ为体（或面、线）密度；dτ为相当于ρ的体（或面、线）元；积分在具有分布密度ρ的整个物质体（或面、线）上进行。

由牛顿运动定律或质点系的动量定理，可推导出质心运动定理：质心的运动和一个位于质心的质点的运动相同，该质点的质量等于质点系的总质量，而该质点上的作用力则等于作用于质点系上的所有外力平移到这一点后的矢量和。

由这个定理可推知：①质点系的内力不能影响质心的运动。

②若质点系所受外力的主矢始终为零，则其质心作匀速直线运动或保持静止状态。

③若作用于质点系上外力的主矢在某一轴上的投影始终为零，则质心在该轴上的坐标匀速变化或保持不变。

质点系的任何运动一般都可分解为质心的平动和相对于质心的运动。

质点系相对某一静止坐标系的动能等于质心的动能和质点系相对随质心作平动的参考系运动的动能之和。

质心位置在工程上有重要意义，例如要使起重机保持稳定，其质心位置应满足一定条件；飞机、轮船、车辆等的运动稳定性也与质心位置密切相关；此外，若高速转动飞轮的质心不在转动轴线上，则会引起剧烈振动而影响机器正常工作和寿命。