七年级二元一次方程组复习讲义

数学七年级下册讲义第7讲二元一次方程模块一基础多元一次方程组知识导航1、二元一次方程的定义含有两个未知数，并且含未知数的项的次数都是1，像这样的方程叫二元一次方程。

例如，25x y+=，20u v-=，132m n=等，都是二元一次方程。

2、二元一次方程组的定义含有两个未知数，每个未知数的项的次数都是1，并且一共有两个方程，像这样的方程组叫做二元一次方程组。

例如，2323521x y x yx y x⎧+=+=⎧⎪⎨⎨-==⎪⎩⎩，等都是二元一次方程组。

3、二元一次方程组的基本解法方法方法1：代入消元法：方法2：加减消元法。

题型一解二元一次方程组例题1解下列方程组：（1）430210x yx y-=⎧⎨-=-⎩.（2）134342 x yx y⎧-=⎪⎨⎪-=⎩.题型二解三元一次方程组例题2解方程组：34145217 223 x y zx y zx y z++=⎧⎪++=⎨⎪+-=⎩练习2解方程组：（1）751 x yx y zx y z+=⎧⎪++=⎨⎪--=⎩.（2）5 428 9313 a b ca b ca b c++=⎧⎪-+=⎨⎪++=⎩.总结归纳注意事项：①当解方程组需要进行通分时，需要注意每一项都要乘以分母的最小公倍数，切勿漏乘；②区分清楚通分和分子分母整数化（分子分母同时扩大或缩小相同倍数，分数的大小不变）的区别；模块二含参方程组题型一整体思想与含参方程例题3已知二元一次方程组()()()()235231x y x yx y x y++-=⎧⎪⎨+--=-⎪⎩，则1x=，y=________．练习3解方程组：()() 2152110 1217102x yx y⎧--++=⎪⎨-+-=⎪⎩.例题4若关于x y 、的二元一次方程组3526x my x ny -=⎧⎨+=⎩的解是12x y =⎧⎨=⎩，则关于a b 、的二元一次方程组()()()()3526a b m a b a b n a b +--=⎧⎪⎨++-=⎪⎩的解是________． 练习4已知关于,x y 的二元一次方程组111222a xb yc a x b y c +=⎧⎨+=⎩的解为34x y =⎧⎨=⎩，则关于,x y 的方程组1112223434a x b y c a x b y c -=⎧⎨-=⎩的解为________． 题型二 含参方程组解的关系例题5关于x y 、方程组2564x y ax by +=-⎧⎨-=⎩与关于x y 、的方程组35168x y bx ay -=⎧⎨+=-⎩的解相同，试求出2017(2)a b +的值.练习51.已知方程组42x y x y m-=⎧⎨+=⎩中,x y 的互为相反数，则m 的值为（ ）. A.2 B.-2 C.0 D.42.已知方程组352,23x y k x x y k +=+⎧⎨+=⎩与y 的值之和等于2，则k 的值为（ ）. A.4 B.-4 C.3 D.-3 题型三 含参方程组的整数解问题例题61.方程27x y +=的解有________个，其中正整数解它们是________.2.已知m 为整数，方程组436626x y x my -=⎧⎨+=⎩有正整数解，则m =________ 练习6若a 为自然数，m n 、是方程组3210033220n m a n m a +=-⎧⎨-=-⎩的解，且m n 、均为正整数，则该方程组的所有解的组数是________.题型四 含参方程组解的存在性 例题7已知方程组531x y ax y b -=⎧⎨+=-⎩①无数多个解；②唯一解；③无解.分别求三种情况下a b 、的值.练习7已知关于x y 、的方程组()312y kx b y k x =+⎧⎨=-+⎩，当k b 、为何值时，方程组： ①有唯一一组解；②无解；③有无穷多组解.巩固加油站巩固1解下列方程组.（1）661x y x y -=⎧⎨=+⎩.（2）3425212x y x y -=⎧⎨+=⎩.巩固2解方程组：（1）32123253x y y z x z -=⎧⎪+=⎨⎪+=⎩①②③.（2）3213272312x y z x y z x y z ++=⎧⎪++=⎨⎪+-=⎩①②③.巩固3关于x y 、的方程组31428mx ny x y +=⎧⎨+=⎩与5236x ny n x y -=-⎧⎨-=⎩有相同的解，则m n -=________. 巩固4若关于x y 、的方程组3522718x y a x y a -=⎧⎨+=-⎩的解互为相反数，则此方程组的解为x =________；y =________.巩固5对于二元一次方程210x y +=. （1）求其正整数解. （2）若7x y +=，求,x y 的值.巩固6当m n 、为何值时，关于x y 、的方程组()214mx y n m x y -=-⎧⎨--=-⎩. （1）无解.（2）唯一解. （3）有无数多解.。

二元一次方程组知识点一（二元一次方程和方程组）【知识梳理】1、二元一次方程：含有两个未知数，并且含有未知数项的次数都是1的方程。

注意：满足的四个条件：1、都是整式方程；2、只含有两个未知数；3、未知数的项最高次数都是一次；4、含有未知数的项的系数不为0.2、二元一次方程组：含有两个未知数的两个一次方程所组成的一组方程叫二元一次方程组。

注意：1）满足的三个条件：1、每个方程都是一次方程；2、方程组具有两个未知数；3、每个方程均为整式方程。

2）方程组的各个方程中，相同字母必须代表同一数量，否则不能将两个方程合在一起，组成方程组。

3.列方程组解应用题的基本思想列方程组解应用题，是把“未知”转换成“已知”的重要方法，它的关键是把已知量和未知量联系起来，找出题目中的等量关系．一般来说，有几个未知量就必须列出几个方程，所列方程必须满足：①方程两边表示的是同类量：②同类量的单位要统一；③方程两边的数要相等.4.列二元一次方程组解应用题的一般步骤：设：用两个字母表示问题中的两个未知数；列：列出方程组（分析题意，找出两个等量关系，根据等量关系列出方程组）；解：解方程组，求出未知数的值；验：检验求得的值是否正确和符合实际情形；答：写出答案．【例题精讲】例题引入（1）如果设这个班有x名女同学，y名男同学.由女生人数的一半比男生人数少15人，可得什么方程？答：______.由再来4名女同学，男女生人数就相等了，你能得怎样的方程？答：______. （2）如果设小华买了x 张80分的邮票，y 张2元的邮票，你能得到怎样的方程？答：______.例1. 下列方程①x x 263=+，②3=xy ，③42=-x y ，④y y x 2410=-，⑤21=+y x ，⑥532=+xy x ，⑦03=+-z y x ，⑧1332=+y x 中，二元一次方程有 个。

例2. 下列方程组中，不是二元一次方程组的是（ ）.A.⎩⎨⎧+==-13032x y y xB.⎩⎨⎧=-=+211z y xC.⎩⎨⎧=+-=+63222y x y x x x D.⎩⎨⎧-=+=6352x x y例3. 若321325a b b x y +---=是二元一次方程，则a = ，b = ．例4、 以⎩⎨⎧-==11y x 为解的二元一次方程组是（ ）.A.⎩⎨⎧=-=+10y x y x B.⎩⎨⎧-=-=+10y x y x C.⎩⎨⎧=-=+20y x y x D.⎩⎨⎧-=-=+20y x y x例5、 若⎩⎨⎧-==22y x 是二元一次方程3=+by ax 的一个解，则=--1b a .例6、 写出5=+y x 的一组正整数解 ；题型二 代入法解法二元一次方程组例1、在方程3)(3)(2=--+x y y x 中，用含x 的代数式表示y ，则 （ ） A 、35-=x y B 、3--=x y C 、35+=x y D 、35--=x y 例2、用代入法解方程组5341x y x y =+⎧⎨+=⎩ . ⎪⎩⎪⎨⎧=+=+14766.0532.0y x y x ；题型三 加减法解二元一次方程组⎩⎨⎧=-=+.732,423t s t s ⎪⎪⎩⎪⎪⎨⎧=+-=-.732,143n m nm题型四 二元一次方程组解法的运用例1、方程组43235x y kx y -=⎧⎨+=⎩的解x y 与的值相等，则k 的值是 .例2、小明和小华同时解方程组5213mx y x ny +=⎧⎨-=⎩，小明看错了m ，解得722x y ⎧=⎪⎨⎪=-⎩小华看错了n ，解得37x y =⎧⎨=-⎩，你能知道原方程组正确的解吗？请求出来．例3、阅读下列解方程组的方法，然后解决有关问题． 解方程组191817171615x y x y +=⎧⎨+=⎩①②时，我们如果直接考虑消元，那将是非常麻烦的，而采用下面的解法则是轻而易举的.①－②，得222x y +=，所以1x y +=．③ ③×16，得161616x y += ④，②－④，得1x =-，从而2y =．所以原方程组的解是12x y =-⎧⎨=⎩．请你用上述方法解方程组200820072006200620052004x y x y +=⎧⎨+=⎩，【课堂练习】1. 有一些苹果箱，若每只装苹果25kg，则剩余40kg无处装；若每只装30kg，则还有20个空箱，这些苹果箱有( ) .A．12只 B．6只 C．112只 D．128只2.幸福中学七年级学生到礼堂开会，若每条长椅坐5人，则少10条长椅，若每条长椅坐6人，则又多余2条长椅，设学生有x人，长椅有y条，依题意得方程组 ( ) .A．5105662x yx y=+⨯⎧⎨=-⨯⎩B．51062x yx y=-⎧⎨=+⎩C．5105662x yx y=-⨯⎧⎨=+⨯⎩D．51062x yx y=+⎧⎨=-⎩3.某校春季运动会比赛中，八年级(1)班、(5)班的竞技实力相当，关于比赛结果，甲同学说：(1)班与(5)班得分比为6:5；乙同学说：(1)班得分比(5)班得分的2倍少40分，若设(1)班得x分，(5)班得y分，根据题意所列的方程组应为 ( ) .A．65240x yx y=⎧⎨=-⎩B．65240x yx y=⎧⎨=+⎩C．56240x yx y=⎧⎨=+⎩D．56240x yx y=⎧⎨=-⎩4.王力在一天内以每件80元的价格卖了两件上衣，其中一件赢利20％，一件赔了20％，则在这次买卖中他( ) .A．赔了10元 B．赚了10元 C．赔了约7元 D．赚了约7元二、填空题5．端午节时，王老师用72元钱买了荷包和五彩绳共20个．其中荷包每个4元，五彩绳每个3元，设王老师购买荷包x个，五彩绳y个，根据题意，列出的方程组是________．6．如图，母亲节那天，很多同学给妈妈准备了鲜花和礼盒．从图中信息可知，买5束鲜花和5个礼盒的总价为 _______ 元．7．一张试卷有25道题，做对一道得4分，做错一道扣1分，小明做了全部试题共得70分，则他做对了______道题.8．已知甲数的2倍比乙数大30，乙数的3倍比甲数的4倍少20，求甲、乙两数，若设甲、乙两数分别为x、y，可得方程组________，这两数分别为________．知识点二（二元一次方程的解法）【知识梳理】1.列方程组解应用题的基本思想列方程组解应用题，是把“未知”转换成“已知”的重要方法，它的关键是把已知量和未知量联系起来，找出题目中的等量关系．一般来说，有几个未知量就必须列出几个方程，所列方程必须满足：①方程两边表示的是同类量：②同类量的单位要统一；③方程两边的数要相等.2.列二元一次方程组解应用题的一般步骤：设：用两个字母表示问题中的两个未知数；列：列出方程组（分析题意，找出两个等量关系，根据等量关系列出方程组）；解：解方程组，求出未知数的值；验：检验求得的值是否正确和符合实际情形；答：写出答案．【例题精讲】题型1 运用某些概念列方程求解在学习过程中，我们常常会遇到二元一次方程的未知数的指数是一个字母或关于字母的代数式，让我们求字母的值，这时巧用定义，可简便地解决这类问题例1. 若01212=+--++b a b a y x 是关于x,y 的二元一次方程,则a =_______,b =_______.题型2 列方程组解决实际问题方程组是描述现实世界的有效数学模型,在日常生活、工农业生产、城市规划及国防领域都有广泛的应用，列二元一次方程组的关键是寻找相等关系，寻找相等关系应以下两方面入手；（1）仔细审题，寻找关键词语；（2）采用画图、列表等方法挖掘相等关系.例2. 一项工程甲单独做需12天完成，乙单独做需18天完成，计划甲先做若干后离去，再由乙完成，实际上甲只做了计划时间的一半因事离去，然后由乙单独承担，而乙完成任务的时间恰好是计划时间的2倍，则原计划甲、乙各做多少天？列方程解下列问题1、有甲乙两种债券，年利率分别是10%与12%，现有400元债券，一年后获利45元，问两种债券各有多少？2、一种饮料大小包装有3种，1个中瓶比2小瓶便宜2角，1个大瓶比1个中瓶加1个小瓶贵4角，大、中、小各买1瓶，需9元6角。

全方位教学辅导教案学 科： 数学 任课教师： 授课时间： 2020 年 月 日 （星期 ） 【针对性训练】一、 课前检测1、下列方程组中是二元一次方程组的是（ ） A ．⎩⎨⎧=-=+232y x y x B ．⎩⎨⎧=+=31y x xy C ．⎩⎨⎧=+=523y x D ．⎩⎨⎧=-=+63832z x y x 2、方程ax －4y=x －1是二元一次方程，则a 的取值为（ ）A ． a≠0B ．a≠－1C ．a≠1D ．a≠23、下列说法正确的是（ ）A ．二元一次方程只有一个解B ．二元一次方程组有无数个解C ．二元一次方程组的解必是它所含的二元一次方程的解D ． ．三元一次方程组一定由三个三元一次方程组成 4、一个二元一次方程的解集，是指这个方程的（ ）A ． 一个解B ．两个解C ．三个解D ．所有解组成的集合5、关于x 的方程()()()512422+=++++-m y m x m x m ，当m = 时，是一元一次方程；当m =时，它是二元一次方程． 6、若方程3y )2a (x1a =-+-是二元一次方程，则a 的取值范围是（ ）A ．a ＞2B ．a=2C ．a=﹣2D ．a ＜﹣2二、知识点讲解➢ 一、二元一次方程的概念含有两个未知数(一般设为x 、y)，并且含有未知数的项的次数都是1，像这样的方程叫做二元一次方程．如x ＋y ＝24，y 32x =+都是二元一次方程． 二元一次方程的一般式：0ax by c ++=（a 、b 、c 均为系数，a≠0，b≠0） ➢ 二、二元一次方程的解使二元一次方程左右两边的值相等的两个未知数的值，叫做二元一次方程的解． 注意：1. 二元一次方程的解是一对数值，如⎩⎨⎧==0y 2x 是二元一次方程x ＋y ＝2的解；2. 每个二元一次方程都有无数组解；3. 在二元一次方程的无数组解中，每组解的一对数值是一一对应的． ➢ 三、二元一次方程组的概念把具有相同未知数的两个二元一次方程合在一起，就组成了一个二元一次方程组．例如，都是二元一次方程组．注意：如果两个一次方程合起来共有两个未知数，这样的方程组也是二元一次方程组．例如，也是二元一次方程组．➢ 四、二元一次方程组的解一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解． 注意：1. 方程组的解是一对数值．2. 一般地，二元一次方程组的解只有一组，但也有特殊情况，如方程组无解，而方程组的解有无数个．3. 二元一次方程组的解满足方程组的每一个方程．4. 二元一次方程组解的讨论：⎩⎨⎧=++=++0222111c y b x a c y b x a （系数均不为0）①当2121b b a a ≠时，方程组有唯一一组解（可用加减消元法求解） ②当212121c c b b a a ≠=时，方程组无解（两个方程是矛盾的） ③当212121c c b b a a ==时，方程组有无穷多个解（两个方程等效）三、题型训练【题型一】二元一次方程组的概念【例1】 下列方程中，是二元一次方程的是（ ）A ．3x －2y=4zB ．6xy+9=0C ．1x+4y=6 D ．4x=24y - 【例2】 下列各式，属于二元一次方程的个数有（ ）①xy+2x －y=7； ②4x+1=x －y ； ③1x+y=5； ④x=y ； ⑤x 2－y 2=2 ⑥6x －2y ⑦x+y+z=1 ⑧y （y －1）=2y 2－y 2+x A ．1 B ．2 C ．3 D ．4【例3】 下列方程组中，是二元一次方程组的是（ ）A ．228423119 (237)54624x y x y a b x B C D x y b c y x x y +=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩ 【例4】 方程3x m ＋1－2y n ＋2＝4是二元一次方程，则m ＝____，n ＝____．变式练习1、下列方程组中，属于二元一次方程组的是（ ）A ． ⎪⎩⎪⎨⎧=+=+725y x y x B ．⎪⎩⎪⎨⎧=-=+043512y x x y xC ．⎪⎩⎪⎨⎧=+=y y x y x 343453D ．⎩⎨⎧=+=-yy x y x 123822、 若x 3m −3﹣2y n −1=5是二元一次方程，则m=_________，n=_________．3、 已知关于x 、y 的方程2x m −3+3y n −1=8是二元一次方程，则m+n 的值为 ．【题型二】二元一次方程组的解【例4】 若3270x y --=，则696y x --的值为 ．【例5】 二元一次方程4x-3y=12，当x=0，1，2，3时，y= ． 【例6】 若(4x-3)2+|2y+1|=0，则x+2= ．【例7】 在式子3m+5n －k 中，当m=－2，n=1时，它的值为1；当m=2，n=－3时，它的值是 ． 【例8】 在x+3y=3中，若用x 表示y ，则y=________，用y 表示x ，则x=__________． 【例9】 写出一个解为⎩⎨⎧-==13y x 的二元一次方程___________________．变式练习1、已知332=-y x ，则代数式596+-y x 的值为2、 对二元一次方程2(5－x)－3(y －2)=10，当x=0时，则y=__________；当y=0时，则x=__________．3、若ｘ、ｙ为非负数，则方程y x 512-=的解是（ ）A ． 无解B ．无数个解C ．唯一一个解D ．不能确定 4、二元一次方程7x+y=15有几组正整数解 ( )A ． 1组B ．2组C ．3组D ．4组 5、方程2x+y=5的正整数解是 ．． 6、 方程2x+y=9在正整数范围内的解有 ．7、对于任何a 值，关于x ，y 的方程ax+（a-1）y=a+1都有一个与a 无关的解，这个解是（ ）A.⎩⎨⎧-==12y x B ．⎩⎨⎧==12y x C ．⎩⎨⎧=-=12y x D ．⎩⎨⎧-=-=12y x8、4x+1=m (x －2)+n (x －5)，则m 、n 的值是（ ）A ． A . ⎩⎨⎧-=-=14n mB ．⎩⎨⎧==14n mC ．⎩⎨⎧-==37n nD ．⎩⎨⎧=-=37n m9、关于y x 、的方程3623-=+k y kx ，对于任何k 的值都有相同的解，试求它的解．【课堂检测】1．下列方程中，属于二元一次方程的是( )A ．3x-2y=5 B.x ²+y=1 C ．x-3=2x D.651=+y x2．已知关于x ，y 的方程81||56-++m n y x是二元一次方程，则m=____，n=____．3．下列方程组中，不是二元一次方程组的是________，①⎩⎨⎧=-=+;254,10y x y x ②⎩⎨⎧==;5,3y x ③⎪⎩⎪⎨⎧=+=+;21,42y x y x ④⎪⎩⎪⎨⎧=-=+;52,32y x y x4.下列三组数值：①⎩⎨⎧==;2,1y x ②⎩⎨⎧==;2,3y x ③⎩⎨⎧=-=;3,2y x 其中是方程2x-y=4的解的是( )A. ① B ．② C ．③ D.①③5．解为⎩⎨⎧==;2,1y x 的方程组是( )A.⎩⎨⎧=+=-;53,1y x y xB.⎩⎨⎧=--=-;53,1y x y xC.⎩⎨⎧=-=-;13,3y x y xD.⎩⎨⎧=+-=-;53,32y x y x 6．在①⎩⎨⎧==,0,0y x ②⎩⎨⎧=-=,1,2y x ③⎩⎨⎧==,2,2y x ④⎪⎩⎪⎨⎧=-=,21,1y x 这四对数值中，____是x-y=0的解，____是x+2y=0的解，因此______是方程组⎩⎨⎧=+=-,02,0y x y x 的解．7．已知关于x ，y 的二元一次方程组⎩⎨⎧-=-=+37,24by x y ax 的解是⎩⎨⎧==,2,1y x 求(a+b)³的值．8．如果方程组⎩⎨⎧=+=+162,★y x y x 的解为⎩⎨⎧==■6y x ．那么被“★”“■”遮住的两个数分别是( )A.10，4B.4，10C.3，10D.10，39．已知⎩⎨⎧-=-=2,3y x 是方程组⎩⎨⎧=-=+2,1by cx cy ax 的解，则a 、b 间的关系是( )A ．4b-9a=1B ．3a+2b=1C ．4b-9a= -1D ．9a+4b=110．请写出一个以x ，y 为未知数的二元一次方程组，且同时满足下列两个条件：①由两个二元一次方程组成，②方程组的解为⎩⎨⎧==,3,2y x这样的方程组可以是________________． 11. 若()22320x y x -++=，则xy的值是_________ ． 12．2x 与8y 的和的2倍是10，则可用方程表示为______________.13．算筹是中国古代用来记数、列式和进行各种数与式演算的一种工具．在算筹记数法中，以“立”“卧”两种排列方式来表示单位数目，表示多位数时，个位用立式，十位用卧式，百位用立式，千位用卧式，以此类推，《九章算术》的“方程”一章中介绍了一种用“算筹图”解决一次方程组的方法．如图①，从左向右的符号中，前两个符号分别代表未知数x ，y 的系数，且根据此图可以列出方程：x+10y= 26.请你根据图②列出方程组：________.二、解答题20．已知两个二元一次方程：①3x -y=0, ②7x -2y=2.(1)对于给出x 的值,在下表中分别写出对应的y 的值；(2)请你写出方程组的解.能力提升如图．小红和小明两人共同解方程组：⎩⎨⎧-=-=+②.24①,155byxyax根据以上他们的对话内容，请你求出a，b的正确值，并计算20171012018⎪⎭⎫⎝⎛-+ba的值．【课后作业】一、选择题1．下列各对x，y的值不是二元一次方程3x+2y=7的解的是( )A．⎩⎨⎧==21yxB．⎩⎨⎧-==13yxC．⎩⎨⎧-==45yxD．⎩⎨⎧-=-=51yx2．如果⎩⎨⎧=-=1,2yx是二元一次方程mx+y=3的一个解，则m的值是( )A.-2B.2C.-1 D．13．下列各组数中，是二元一次方程组⎩⎨⎧=-=+42,2yxyx的解的是( )A．⎩⎨⎧==2,0yxB．⎩⎨⎧==,2yxC.⎩⎨⎧-==1,3yxD.⎩⎨⎧==11yx4．已知⎩⎨⎧=-=2,1yx是二元一次方程组⎩⎨⎧=-=+1,23ynxmyx的解，则m-n的值是( ) A．1 B．2 C.3 D.45．如果x=3，y=2是方程6x+by=32的解，则b= ．6．已知2,3x y =-⎧⎨=⎩是方程x －ky=1的解，那么k= ．7．若是关于x 、y 的二元一次方程ax ﹣3y=1的解，则a 的值为（ ）A ． ﹣5B ．﹣1C ．2D ．78．为了丰富学生课外活动，培养学生动手操作能力，王老师让学生把5 m 长的彩绳截成2m 或 1m 的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法( ) A.1 B.2 C ．3 D ．4二、填空题3．已知关于x 、y 的方程112433=++-n y m x 是二元一次方程，则m+n 的值为______．4．下面三组数据：①⎩⎨⎧-==;5,1y x ②⎩⎨⎧-==;3,2y x ③⎩⎨⎧-=-=;1,2y x ； 满足方程2x-y=7的是____，满足方程x+2y= -4的是_______，同时满足这两个方程的是_______，故二元一次方程组⎩⎨⎧-=+=-42,72y x y x 的解是_______．（填序号）4．若关于x 、y 的二元一次方程3x-ay=1有一个解是⎩⎨⎧==,2,3y x ．则a=_________.课堂检测答案1.A 2．9;0 3．③④ 4．B 5.D 6．①③；①②④；①7．解析 把⎩⎨⎧==2,1y x 代入原方程组，得⎩⎨⎧-=-=+②,327①,28b a由①得a= -6，由②得b=5，所以(a+b)³=（- 6+5）³=-1．8．A 9.D 10．答案⎩⎨⎧-=-=+.1,5y x y x （答案不唯一） 11．32-12. 4x+16y=10 13.答案⎩⎨⎧=+=+18222y x y x 能力提升解析 因为小明看错了①中的a ，所以⎩⎨⎧-=-=1,3y x 满足方程②，即4×（-3）-b ×（-1）=-2，解得b=10；因为小红看错了②中的b ，所以⎩⎨⎧==4,5y x 满足方程①，即5a+5×4= 15，解得a=-1．所以20171012018⎪⎭⎫ ⎝⎛-+b a =20172018)10101()1(⨯-+-=1+（-1）=0．课后作业答案一、选择题 D C B DC 二、填空题 3．34． ①②；②③；②；② 4． 4。

⼈教七年级数学⼆元⼀次⽅程组和⼀元⼀次不等式组复习讲义⼆元⼀次⽅程组相关知识归纳1.⼆元⼀次⽅程⼆元⼀次⽅程具备以下四个特征：（1）是⽅程；（2）有且只有两个未知数；（3）⽅程是整式⽅程，即各项都是整式；（4）各项的最⾼次数为1.2.⼆元⼀次⽅程的解.3.⼆元⼀次⽅程组.它有两个特点：⼀是⽅程组中每⼀个⽅程都是⼀次⽅程；⼆是整个⽅程组中含有两个且只含有两个未知数.4.⼆元⼀次⽅程组的解.1概念：将⽅程组中⼀个⽅程的某个未知数⽤含有另⼀个未知数的代数式表⽰出来，代⼊另⼀个⽅程中，消去⼀个未知数，得到⼀个⼀元⼀次⽅程，最后求得⽅程组的解. 这种解⽅程组的⽅法叫做代⼊消元法，简称代⼊法. （2）代⼊法解⼆元⼀次⽅程组的步骤①选取⼀个系数较简单的⼆元⼀次⽅程变形，⽤含有⼀个未知数的代数式表⽰另⼀个未知数；②将变形后的⽅程代⼊另⼀个⽅程中，消去⼀个未知数，得到⼀个⼀元⼀次⽅程（在代⼊时，要注意不能代⼊原⽅程，只能代⼊另⼀个没有变形的⽅程中，以达到消元的⽬的. ）；③解这个⼀元⼀次⽅程，求出未知数的值；④将求得的未知数的值代⼊①中变形后的⽅程中，求出另⼀个未知数的值；⑤⽤“{”联⽴两个未知数的值，就是⽅程组的解；⑥最后检验求得的结果是否正确（代⼊原⽅程组中进⾏检验，⽅程是否满⾜左边＝右边）.加减消元法2概念：当⽅程中两个⽅程的某⼀未知数的系数相等或互为相反数时，把这两个⽅程的两边相加或相减来消去这个未知数，从⽽将⼆元⼀次⽅程化为⼀元⼀次⽅程，最后求得⽅程组的解，这种解⽅程组的⽅法叫做加减消元法，简称加减法. （2）加减法解⼆元⼀次⽅程组的步骤①利⽤等式的基本性质，将原⽅程组中某个未知数的系数化成相等或相反数的形式；②再利⽤等式的基本性质将变形后的两个⽅程相加或相减，消去⼀个未知数，得到⼀个⼀元⼀次⽅程（⼀定要将⽅程的两边都乘以同⼀个数，切忌只乘以⼀边，然后若未知数系数相等则⽤减法，若未知数系数互为相反数，则⽤加法）；③解这个⼀元⼀次⽅程，求出未知数的值；④将求得的未知数的值代⼊原⽅程组中的任何⼀个⽅程中，求出另⼀个未知数的值；⑤⽤“{”联⽴两个未知数的值，就是⽅程组的解；⑥最后检验求得的结果是否正确（代⼊原⽅程组中进⾏检验，⽅程是否满⾜左边＝右边）.【⼩结】解⼆元⼀次⽅程组可以⽤代⼊法，也可以⽤加减法．⼀般地说，当⽅程组中有⼀个⽅程的某⼀个未知数的系数的绝对值是1或有⼀个⽅程的常数项是0时，⽤代⼊法⽐较⽅便；当两个⽅程中某⼀未知数的系数的绝对值相等或成整数倍时，⽤加减法⽐较⽅便．(1)、三元⼀次⽅程的概念(2)、三元⼀次⽅程组的概念(3)、三元⼀次⽅程组的解法三元⼀次⽅程组解题的基本步骤：①利⽤代⼊法或加减法，把⽅程组中的⼀个⽅程与另两个⽅程分别组成两组，消去两组中的同⼀个未知数，得到关于另外两个未知数的⼆元⼀次⽅程组。

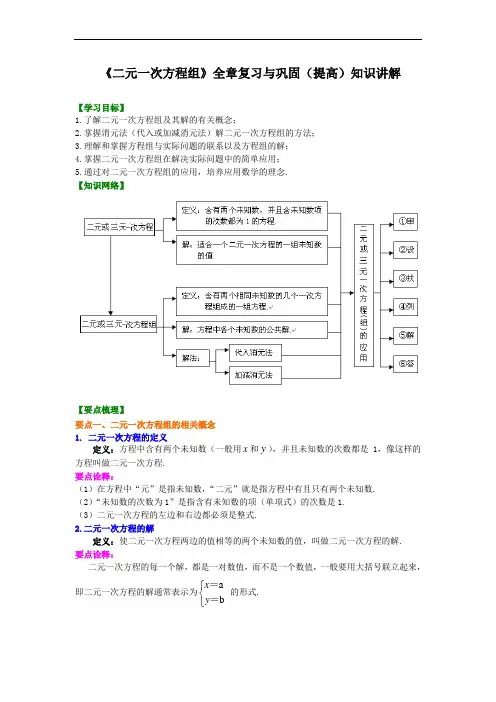
《二元一次方程组》全章复习与巩固（提高）知识讲解【学习目标】1.了解二元一次方程组及其解的有关概念；2.掌握消元法（代入或加减消元法）解二元一次方程组的方法；3.理解和掌握方程组与实际问题的联系以及方程组的解；4.掌握二元一次方程组在解决实际问题中的简单应用；5.通过对二元一次方程组的应用，培养应用数学的理念. 【知识网络】【要点梳理】要点一、二元一次方程组的相关概念 1. 二元一次方程的定义定义：方程中含有两个未知数（一般用x 和y ），并且未知数的次数都是1，像这样的方程叫做二元一次方程. 要点诠释：（1）在方程中“元”是指未知数，“二元”就是指方程中有且只有两个未知数. （2）“未知数的次数为1”是指含有未知数的项（单项式）的次数是1. （3）二元一次方程的左边和右边都必须是整式. 2.二元一次方程的解定义：使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解. 要点诠释：二元一次方程的每一个解，都是一对数值，而不是一个数值，一般要用大括号联立起来，即二元一次方程的解通常表示为⎩⎨⎧b a＝＝y x 的形式.3. 二元一次方程组的定义定义：把具有相同未知数的两个二元一次方程合在一起，就组成了一个二元一次方程组. 此外，组成方程组的各个方程也不必同时含有两个未知数.例如，二元一次方程组3452x y x +=⎧⎨=⎩. 要点诠释：（1）它的一般形式为111222a xb yc a x b y c +=⎧⎨+=⎩（其中1a ，2a ，1b ，2b 不同时为零）．（2）更一般地，如果两个一次方程合起来共有两个未知数，那么它们组成一个二元一次方程组．（3）符号“{”表示同时满足，相当于“且”的意思．4. 二元一次方程组的解定义：一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解. 要点诠释：（1）方程组中每个未知数的值应同时满足两个方程，所以检验是否是方程组的解，应把数值代入两个方程，若两个方程同时成立，才是方程组的解，而方程组中某一个方程的某一组解不一定是方程组的解.（2）方程组的解要用大括号联立；（3）一般地，二元一次方程组的解只有一个，但也有特殊情况，如方程组⎩⎨⎧=+=+6252y x y x 无解，而方程组⎩⎨⎧-=+-=+2221y x y x 的解有无数个.要点二、二元一次方程组的解法1.解二元一次方程组的思想转化消元一元一次方程二元一次方程组2.解二元一次方程组的基本方法：代入消元法和加减消元法 （1）用代入消元法解二元一次方程组的一般过程：①从方程组中选定一个系数比较简单的方程进行变形，用含有x （或y ）的代数式表示y （或x ），即变成b ax y +=（或b ay x +=）的形式； ②将b ax y +=（或b ay x +=）代入另一个方程（不能代入原变形方程）中，消去y （或x ），得到一个关于x （或y ）的一元一次方程； ③解这个一元一次方程，求出x （或y ）的值；④把x （或y ）的值代入b ax y +=（或b ay x +=）中，求y （或x ）的值； ⑤用“{”联立两个未知数的值，就是方程组的解.要点诠释：(1)用代入法解二元一次方程组时，应先观察各项系数的特点，尽可能选择变形后比较简单或代入后化简比较容易的方程变形；(2)变形后的方程不能再代入原方程，只能代入原方程组中的另一个方程； (3)要善于分析方程的特点，寻找简便的解法.如将某个未知数连同它的系数作为一个整体用含另一个未知数的代数式来表示，代入另一个方程，或直接将某一方程代入另一个方程，这种方法叫做整体代入法.整体代入法是解二元一次方程组常用的方法之一，它的运用可使运算简便，提高运算速度及准确率.（2）用加减消元法解二元一次方程组的一般过程：①根据“等式的两边都乘以（或除以）同一个不等于0的数，等式仍然成立”的性质，将原方程组化成有一个未知数的系数绝对值相等的形式； ②根据“等式两边加上（或减去）同一个整式，所得的方程与原方程是同解方程”的性质，将变形后的两个方程相加（或相减），消去一个未知数，得到一个一元一次方程； ③解这个一元一次方程，求出一个未知数的值；④把求得的未知数的值代入原方程组中比较简单的一个方程中，求出另一个未知数的值； ⑤将两个未知数的值用“{”联立在一起即可.要点诠释：当方程组中有一个未知数的系数的绝对值相等或同一个未知数的系数成整数倍时，用加减消元法较简单.要点三、实际问题与二元一次方程组要点诠释：（1）解实际应用问题必须写“答”，而且在写答案前要根据应用题的实际意义，检查求得的结果是否合理，不符合题意的解应该舍去； （2）“设”、“答”两步，都要写清单位名称；（3）一般来说，设几个未知数就应该列出几个方程并组成方程组. 要点四、三元一次方程组1．定义：含有三个未知数，并且含有未知数的项的次数都是1的方程叫做三元一次方程；含有三个相同的求知数，每个方程中含未知数的项的次数都是1，并且一共有三个方程，像这样的方程组叫做三元一次方程组.412,325,51,x y z x y z x y z +-=⎧⎪++=-⎨⎪-+=⎩ 273,31,34a b a c b c +=⎧⎪-=⎨⎪-+=⎩等都是三元一次方程组. 要点诠释：理解三元一次方程组的定义时，要注意以下几点：（1）方程组中的每一个方程都是一次方程；（2）如果三个一元一次方程合起来共有三个未知数，它们就能组成一个三元一次方程组. 2．三元一次方程组的解法解三元一次方程组的基本思想仍是消元，一般的，应利用代入法或加减法消去一个未知数，从而化三元为二元，然后解这个二元一次方程组，求出两个未知数，最后再求出另一个未知数．解三元一次方程组的一般步骤是：（1）利用代入法或加减法，把方程组中一个方程与另两个方程分别组成两组，消去两组中的同一个未知数，得到关于另外两个未知数的二元一次方程组； （2）解这个二元一次方程组，求出两个未知数的值； （3）将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程，得到一个一元一次方程；（4）解这个一元一次方程，求出最后一个未知数的值； （5）将求得的三个未知数的值用“{”合写在一起． 要点诠释： （1）有些特殊的方程组可用特殊的消元法，解题时要根据各方程特点寻求比较简单的解法． （2）要检验求得的未知数的值是不是原方程组的解，将所求得的一组未知数的值分别代入原方程组里的每一个方程中，看每个方程的左右两边是否相等，若相等，则是原方程组的解，只要有一个方程的左、右两边不相等就不是原方程组的解． 3. 三元一次方程组的应用列三元一次方程组解应用题的一般步骤：（1）弄清题意和题目中的数量关系，用字母(如x ，y ，z )表示题目中的两个(或三个)未知数；（2）找出能够表达应用题全部含义的相等关系；（3）根据这些相等关系列出需要的代数式，从而列出方程并组成方程组； （4）解这个方程组，求出未知数的值； （5）写出答案(包括单位名称)． 要点诠释：(1)解实际应用题必须写“答”，而且在写答案前要根据应用题的实际意义，检查求得的结果是否合理，不符合题意的应该舍去． (2)“设”、“答”两步，都要写清单位名称，应注意单位是否统一． (3)一般来说，设几个未知数，就应列出几个方程并组成方程组． 【典型例题】类型一、二元一次方程组的相关概念1.在下列方程中，只有一个解的是（ ）A . 1330x y x y +=⎧⎨+=⎩ B . 1332x y x y +=⎧⎨+=-⎩ C . 1334x y x y +=⎧⎨-=⎩ D . 1333x y x y +=⎧⎨+=⎩【思路点拨】逐一求每个选项中方程组的解，便得出正确答案 【答案】C .【解析】选项A 、B 、D 中，将方程1x y +=，两边同乘以3得333x y +=，从而可以判断A 、B 选项中的两个二元一次方程矛盾，所以无解；而D 中两个方程实际是一个二元一次方程，所以有无数组解，排除法得正确答案为C. 【总结升华】在111222a xb yc a x b y c +=⎧⎨+=⎩（其中1a ，2a ，1b ，2b 均不为零），（1）当121222a a c a b c =≠时，方程组无解；（2）当121222a a c a b c ==，方程组有无数组解； （3）当1222a a ab ≠，方程组有唯一解． 举一反三：【高清课堂：二元一次方程组章节复习409413 例1（3）】 【变式1】若关于x 、y 的方程()12mm x y ++=是二元一次方程，则m = ．【答案】1．【变式2】已知方程组531x y ax y b -=⎧⎨+=-⎩有无数多个解，则a 、b 的值等于 ．【答案】a ＝﹣3，b ＝﹣14．类型二、二元一次方程组的解法2. (黄冈调考)解方程组2()5335()322x y y x y y ⎧-+=⎪⎪⎨⎪--=-⎪⎩①②【思路点拨】本题结构比较复杂，一般应先化简，再消元．仔细观察题目，不难发现，方程组中的每一个方程都含有(x -y )，因此可以把(x -y )看作一个整体，消去(x -y )可得到一个关于y 的一元一次方程．【答案与解析】解：由①×9得：6(x -y )+9y ＝45 ③ ②×4得：6(x -y )-10y ＝-12 ④ ③-④得：19y ＝57， 解得y ＝3．把y ＝3代入①，得x ＝6．所以原方程组的解是63x y =⎧⎨=⎩．【总结升华】本题巧妙运用整体法求解方程组，显然比加减法或代入法要简单，在平时求方程组的解时，要善于发现方程组的特点，运用整体法求解会收到事半功倍的效果． 举一反三：【变式】(换元思想)解方程组16105610x y x yx y x y +-⎧+=⎪⎪⎨+-⎪-=⎪⎩【答案】 解：设6x y m +=，10x yn -=． 则原方程组可化为15m n m n +=⎧⎨-=⎩，解得32m n =⎧⎨=-⎩．所以36210x y x y +⎧=⎪⎪⎨-⎪=-⎪⎩ 即1820x y x y +=⎧⎨-=-⎩．∴ 119x y =-⎧⎨=⎩．3.（2015•江都市模拟）小明和小文解一个二元一次组小明正确解得小文因抄错了c ，解得已知小文除抄错了c 外没有发生其他错误，求a+b+c的值． 【思路点拨】把代入方程组第一个方程求出c 的值，将x 与y 的两对值代入第二个方程求出a 与b 的值，即可求出a+b+c 的值．【答案与解析】 解：把代入cx ﹣3y=﹣2，得c+3=﹣2，解得：c=﹣5， 把与分别代入ax+by=2，得，解得：，则a+b+c=2+﹣5=3﹣5=﹣2．【总结升华】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．举一反三：【变式】已知二元一次方程组⎪⎪⎩⎪⎪⎨⎧=+=+175194y x y x 的解为a x =，b y =，则=-b a .【答案】11.类型三、实际问题与二元一次方程组4.用8块相同的长方形地砖拼成一块矩形地面，地砖的拼放方式及相关数据如图所示，求每块地砖的长与宽.60cm【思路点拨】初看这道题目中没有提供任何相等关系，但是题目提供的图形隐含着矩形两条宽相等，两条长相等，我们设每个小长方形的长为x ，宽为y ，就可以列出一个关于x 、y 的二元一次方程组. 【答案与解析】解：设每块地砖的长为xc m 与宽为ycm ，根据题意得：6023x y x x y +=⎧⎨=+⎩，解得：4515x y =⎧⎨=⎩ 答：每块地砖长为45cm ，宽为15cm【总结升华】有些题目的相等关系不是直接给我们的，这就需要我们仔细阅读题目，设法提炼出题目中隐含的相等关系.举一反三：【变式】如图，长方形ABCD 中放置9个形状、大小都相同的小长方形（尺寸如图），求图中阴影部分的面积.【答案】解：设每个小长方形的长为x ，宽为y ，根据题意得：422(2)37x y x y y +=⎧⎨+-=⎩，解得103x y =⎧⎨=⎩所以阴影部分的面积为：22(73)922(79)910382y xy +-=+-⨯⨯=. 答：图中阴影部分的面积为82.5.（龙岩）已知：用2辆A 型车和1辆B 型车载满货物一次可运货10吨；用1辆A 型车和2辆B 型车载满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用A 型车a 辆，B 型车b 辆，一次运完，且恰好每辆车都载满货物． 根据以上信息，解答下列问题：（1）1辆A 型车和1辆车B 型车都载满货物一次可分别运货多少吨？ （2）请你帮该物流公司设计租车方案；（3）若A 型车每辆需租金100元/次，B 型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费． 【答案与解析】【总结升华】本题实际上是求二元一次方程组的正整数． 举一反三：【变式1】甲、乙两班学生到集市上购买苹果，价格如下：甲班分两次共购买苹果70千克(第二次多于第一次)，共付出189元，而乙班则一次购买苹果70千克。

专题复习：二元一次方程组【知识概要】1.二元一次方程：像x ＋y ＝2这样的方程中含有两个未知数（x 和y ），并且未知数的指数都是1，这样的方程叫做二元一次方程.2.二元一次方程的解：一般地，使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解.3.二元一次方程组：把两个方程x ＋y ＝3和2x ＋3y ＝10合写在一起为像这样，把两个二元一次方程组合在一起，就组成了一个二元一次方程组.4.二元一次方程组的解：二元一次方程组的两个方程的公共解，叫做二元一次方程组的解.5.代入消元法：由二元一次方程组中的一个方程，把一个未知数用含另一个未知数的式子表示出来，再代入另一方程，实现消元，进而求得这个二元一次方程组的解，这种方法叫做代入消元法，简称代入法.6.加减消元法：两个二元一次方程中同一个未知数的系数相反或相等时，将两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程.这种方法叫做加减消元法，简称加减法.7.二元一次方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解的情况有以下三种：① 当212121c c b b a a ==时，方程组有无数多解。

（∵两个方程等效） ② 当212121c c b b a a ≠=时，方程组无解。

（∵两个方程是矛盾的） ③ 当2121b b a a ≠（即a 1b 2－a 2b 1≠0）时，方程组有唯一的解：⎪⎪⎩⎪⎪⎨⎧--=--=1221211212211221b a b a a c a c y b a b a b c b c x （这个解可用加减消元法求得）8.方程的个数少于未知数的个数时，一般是不定解，即有无数多解，若要求整数解，可按二元一次方程整数解的求法进行。

9.求方程组中的待定系数的取值，一般是求出方程组的解（把待定系数当己知数），再解含待定系数的方程。

【主要思想】一、转化思想“转化”思想就是将复杂的、陌生的问题迁移为简单的、熟悉的问题进行求解，这是学习新知识，研究新问题的一种基本方法.本章中二元一次方程组的解法的实质就是借助“消元”： “二元”转化为“一元”.二、方程的思想将数量关系转化为方程（组）的形式，通过解方程（组）使问题得以解决的思维形式就是方程的思想，用方程的思想解决往往比用其它方法简捷、方便得多。

二元一次方程组本章知识点题型➢ 二元一次方程的定义：含有 个未知数，并且含有未知数的项的次数都是 ，像这样的方程叫做二元一次方程．二元一次方程有 解． ➢ 二元一次方程组的解：一般地，二元一次方程组的两个方程的 ，叫做二元一次方程组的解．一般情况下二元一次方程组的解是 的． ➢ 二元一次方程组的解法：① ；② ． 【例1】二元一次方程（组）定义1. 已知方程2132310n m n x y ---+=是二元一次方程，则m = ，n =．2. 下列方程组中：①202x y x y +=⎧⎨+=⎩；②301x y y -=⎧⎨=⎩；③0232x z x y -=⎧⎨+=-⎩；④12x y =⎧⎨=⎩，其中是二元一次方程组的有 ．（填序号即可） 【例2】二元一次方程（组）的解1. 如果32x y ì=ïí=ïî是方程632x by +=的解，则b =．2. （2017春•辛集市期末）小亮解方程组2212x y x y +=⎧⎨-=⎩●的解为5x y =⎧⎨=⎩★由于不小心滴上了两滴墨水，刚好遮住了两个数●和★，则这两个数分别为 ． 【例3】二元一次方程（组）的解法 1. 解二元一次方程组：（1）23525x y x y ì+=ïí+=ïî；（2）13102428x y x y ì-+-=ïíï-+=-î；2. 已知：y kx b =+且当1x =-时，2y =；当2x =时，7y =-；求：当2x =-时，y 的值．【例4】二元一次方程组的变形若23135x y x y ++==，将原方程组化为111222a xb yc a x b y c ì+=ïí+=ïî的形式为 ．➢ 二元一次方程组满足三个条件：①方程组中的两个方程都是 方程； ②方程组中共含有 未知数； ③每个方程都是一次方程．【例5】系数求解问题在解方程组51044ax yx by+=⎧⎨-=-⎩时，由于粗心，甲看错了方程组中的a，得到的解为31xy=-⎧⎨=-⎩，乙看错了方程组中的b，得到的解为54xy=⎧⎨=⎩．（1）求正确的a，b的值；（2）求原方程组的解．【例6】方程同解1.已知关于x、y的方程组45321x yx y+=⎧⎨-=⎩与方程组31ax byax by+=⎧⎨-=⎩的解相同，求ab的值．2.已知关于x，y的二元一次方程组533321x y nx y n+=⎧⎨+=+⎩的解适合方程6x y+=，求n的值．列二元一次方程组解决实际问题的一般步骤：（1）审题：找出问题中的已知条件和未知量及它们之间的关系． （2）设元：找出题中的两个关键的未知量，并用字母表示出来． （3）列方程组：挖掘题目中的关系，找出两个等量关系，列出方程组． （4）求解．（5）检验作答：检验所求解是否符合实际意义，并作答． 【例8】行程问题A 、B 两地相距36千米，两人步行，甲从A 到B ，乙从B 到A ，两人同时出发，相向而行，4小时后相遇；若行6小时，此时甲剩下的路程是乙所余下的路程的2倍，求两人速度． 【小练】已知某铁路桥长800m ，现有一列火车从桥上通过，测得火车从开始上桥到完全过桥共用45s ，整列火车完全在桥上的时间是35s ，求火车的速度和长度．【例9】工程问题一家商店进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付给两组费用共3520元；若先请甲组单独做6天，再请乙组单独做12天可以完成，需付给两组费用共3480元，那么甲、乙两组单独工作一天，商店应各付多少元？【小练】2台大型收割机和5台小型收割机同时工作2h共收割3.6公顷；3台大型收割机和2台小型收割机同时工作5h共收割8公顷．1台大型收割机和1台小型收割机每小时各收割小麦多少公顷？找等量关系是列方程组的关键和难点，有如下规律和方法：①确定应用题的类型，按其一般规律方法找等量关系．②将问题中给出的条件按意思分割成两个方面，有“；”时一般“；”前后各一层，分别找出两个等量关系．③借助表格提供信息的，按横向或纵向去分别找等量关系．④图形问题，分析图形的长、宽，从中找等量关系．1. 下列方程（组）中，①20x +=；②321x y -=；③10xy +=；④121x x-=；⑤13x y x y +=⎧⎨-=⎩；⑥201x y x z -=⎧⎨+=⎩，其中是二元一次方程的是 ，是二元一次方程组的是 ．（填序号即可）2. 若关于x 、y 的二元一次方程组325x y x ay ì+=ïí-=ïî的解是1x by ì=ïí=ïî，则b a 的值为 ．3. 若234326a b a b ì+=ïí+=ïî，则a b += ．4. 若5232m n x y +与3263m n x y +-是同类项，则m n -= ．5. 解方程组（1）3586510m n m n -=⎧⎨+-=⎩；（2）5115y z x x y z x z y +-=-⎧⎪+-=-⎨⎪+-=⎩．6. 在解关于x ，y 的方程组278ax by cx y +=⎧⎨-=⎩时，老师告诉同学们正确的解是32x y =⎧⎨=-⎩，小明由于看错了系数c ，因而得到的解为22x y =-⎧⎨=⎩，试求a b c ++的值．7. 已知方程组23109x y ax by +=⎧⎨+=⎩与方程组8432bx ay x y -=⎧⎨-=⎩的解相等，试求a 、b 的值．8. （2015•河北模拟）已知关于x ，y 的二元一次方程组236228x y a x y a -=+⎧⎨+=-⎩的解满足x y a -=，求该方程组的解．9. 甲乙两地相距120千米，一辆汽车和一辆摩托车从两地同时出发相向而行，1.2小时相遇．相遇后，摩托车继续前进，汽车在相遇处停留10分钟后原速返回，结果在第一次相遇后半小时再次遇到摩托车，问汽车、摩托车每小时各行驶多少千米？。