力力矩力偶

力偶矩与力矩的区别和联系答案：一、作用不同：力矩是力对物体产生转动作用的物理量。

可以分为力对轴的矩和力对点的矩。

即：M=LxF。

其中L是从转动轴到着力点的距离矢量, F是矢量力；力矩也是矢量。

力偶是作用于同一刚体上的一对大小相等、方向相反、但不共线的一对平行力。

二、含义不同：力偶矩为“力偶的力矩”的简称，亦称“力偶的转矩”。

力矩与力偶矩的联系是物体旋转的作用。

扩展：力矩：力矩表示力对物体作用时所产生的转动效应的物理量。

力和力臂的乘积为力矩。

力矩是矢量。

力对某一点的力矩的大小为该点到力的作用线所引垂线看长度（即力臂）乘以力的大小，其方向则垂直于垂线和力所构成的平面用右手螺旋法则来确定。

力对某一轴线力矩的大小，等于力对轴上任一点的力矩在轴线上的投影。

国际单位制中，力矩的单位是牛顿·米。

常用的单位还有千克力·米等。

力矩能使物体获得角加速度，并可使物体的动量矩发生改变，对同一物体来说力矩愈大，转动状态就愈容易改变。

力矩的计算公式为M=F*L，公式当中M表示的是力F对于转动轴O的力矩，只要是使物体产生逆时针方向转动效果的，称为正力矩，反之则称为负力矩。

力偶距：由两个大小相等方向相反的平行力所组成的二力称为力偶，记为（F,F,），力偶两力之间的垂直距离称为力偶臂，记做d。

力偶不能合成为一个力，也不能通过一个力进行平衡，或是用一个力进行等效替换。

力偶可以使物体转动以及改变物体转动的状态。

力偶对物体的转动效果与力矩对物体的转动效果相同，力偶对物体的作用效应可以通过力偶距来进行衡量。

力偶距的计算可以通过力与力偶臂的乘积得到，计算公式为M=F*d。

只要是使物体产生逆时针方向转动效果的，称为正力偶矩，反之则称为负力偶矩。

力矩和力偶距的异同共同点：单位统一,符号规定统一。

差异点：1.力矩随矩心位置不同而变化；力偶矩对物体作用效果与矩心选取无关。

2.力偶矩可以完全描述一个力偶；力对点之矩不能完全描述一个力偶。

简述力矩和力偶矩的异同力矩和力偶矩是物理学中描述力的概念，它们有一些相似之处，但也有一些区别。

力矩（Torque）：1.定义：力矩是一个力对物体产生旋转运动的影响。

它是通过力与力臂（从轴到力的垂直距离）的乘积来计算的。

2.方向：力矩是一个矢量，具有大小和方向。

它的方向垂直于力的方向和力臂的方向，遵循右手定则。

3.单位：国际单位制中，力矩的单位是牛顿米（N·m）。

4.公式：力矩（τ）等于力（F）乘以力臂（r）：τ=F×r。

5.效果：力矩导致物体绕一个轴点旋转，其方向和速度取决于力的大小和方向以及力臂的长度。

力偶矩（Couple Moment）：1.定义：力偶矩是由一对相等大小但方向相反的力组成的，它们的作用线距离轴相等。

力偶矩的作用结果是不产生平移，只引起物体绕轴点的纯旋转。

2.方向：力偶矩的方向是垂直于作用线的方向，通常定义为“垂直于纸面向外”和“垂直于纸面向内”两种方向。

3.单位：力偶矩的单位与力矩相同，为牛顿米（N·m）。

4.公式：力偶矩的大小等于其中一力的大小乘以力臂，不涉及力的方向：M=F×d。

5.效果：力偶矩导致物体纯粹绕轴点旋转，而不会导致物体的平移。

异同点：•两者都是用来描述力对物体的旋转效应。

•两者都可以用牛顿米（N·m）作为单位。

•力矩是由单个力产生的，而力偶矩是由一对力产生的，它们的作用线距离轴相等。

•力矩具有大小和方向，而力偶矩只有大小，方向垂直于作用线。

总的来说，力矩和力偶矩是在力和旋转运动的背景下用于描述物体行为的重要物理量，它们有不同的定义和效应，但都是重要的工程和物理学概念。

力偶矩和力矩
力偶矩和力矩是物理学中的两个重要概念，它们在力学、机械学等领
域中有着广泛的应用。

力偶矩和力矩的概念虽然相似，但是它们的物
理意义和计算方法却有所不同。

力偶矩是指两个大小相等、方向相反的力在同一平面内作用于同一点
上所产生的力矩。

力偶矩的大小等于两个力的大小乘以它们之间的距离，方向垂直于力所在的平面，符合右手定则。

力偶矩的物理意义是
描述力对物体的扭矩作用，它可以用来计算物体的旋转运动。

力矩是指力对物体产生的转动效应，它等于力的大小乘以力臂的长度。

力臂是指力作用点到物体的旋转轴的垂直距离。

力矩的方向垂直于力
臂和力的平面，符合右手定则。

力矩的物理意义是描述力对物体的转
动效应，它可以用来计算物体的平衡状态和旋转运动。

在实际应用中，力偶矩和力矩常常被用来计算物体的平衡状态和旋转
运动。

例如，在机械设计中，我们需要计算物体所受的力偶矩和力矩，以确定物体的平衡状态和旋转运动。

在航空航天领域中，力偶矩和力
矩也被广泛应用于飞行器的设计和控制中。

总之，力偶矩和力矩是物理学中的两个重要概念，它们在力学、机械
学等领域中有着广泛的应用。

了解力偶矩和力矩的概念和计算方法，对于理解物体的平衡状态和旋转运动有着重要的意义。

动力学中的力矩与力偶推导动力学是研究物体运动的力学分支，力矩与力偶是在动力学中的重要概念。

力矩是描述力对物体的旋转效果，而力偶则是用来描述力矩对物体的作用效果。

在本文中，将详细推导力矩与力偶的定义以及它们在动力学中的应用。

1.力矩的定义与推导在物理学中，力矩又称为力的转矩，它用来描述力对物体产生的旋转效果。

力矩的大小与力的大小以及力与物体转动轴之间的垂直距离有关。

假设一个力F作用在物体上，该力与物体转动轴之间的距离为r，力F的力矩M可以通过以下公式计算：M = F × r其中，M代表力矩，F代表力，r代表力与转动轴之间的距离。

对于多个力作用在同一物体上，其合力矩等于各力矩的矢量和。

若有n个力分别为F1、F2、...、Fn，作用在同一物体上，它们与转动轴的距离分别为r1、r2、...、rn，合力矩M_total可以通过以下公式计算：M_total = F1 × r1 + F2 × r2 + ... + Fn × rn2.力偶的定义与推导力偶是由一对大小相等、方向相反的力组成，它们沿着同一直线作用于物体上。

力偶的作用效果是产生一个力矩，其大小与力的大小相等，方向垂直于该直线。

假设一个力偶大小为F，力偶的力矩M_couple可以通过以下公式计算：M_couple = F × d其中，M_couple代表力偶的力矩，F代表力偶的大小，d代表力偶之间的距离。

当多个力偶作用在同一物体上时，其合力矩等于各力偶力矩的矢量和。

若有n个力偶大小分别为F1、F2、...、Fn，力偶之间的距离分别为d1、d2、...、dn，合力矩M_couple_total可以通过以下公式计算：M_couple_total = F1 × d1 + F2 × d2 + ... + Fn × dn3.力矩与力偶的应用力矩与力偶在动力学中有广泛的应用。

它们常常用于分析刚体的平衡条件、机械系统的运动以及转动运动等。

力偶力矩力偶矩之间的关系
力偶矩、力矩和力偶之间存在以下关系：
- 力矩是一个描述力的转动效果的物理量，它的大小等于力的大小与力臂的乘积，方向垂直于力和力臂所在的平面，是一个矢量。

力臂是从转动轴到力的垂直距离，是描述转动效果的关键因素。

- 力偶是一个成对出现的力，它们等大、反向、作用在同一直线上，但不共点。

力偶矩是描述力偶的转动效果的物理量，它的大小等于力偶中两个力的大小和它们的力臂的乘积，方向垂直于力和力臂所在的平面，也是一个矢量。

- 力偶矩和力矩的区别在于，力矩的大小、正负与力和矩心的相对位置有关；而力偶矩与转动轴的位置无关。

总之，力偶矩、力矩和力偶是描述力的不同物理量，它们的大小、方向和作用效果均有所不同。

在实际应用中，需要根据具体情况选择合适的物理量来描述力的作用。

同学们好！开车是21世纪我们要掌握的一项根本技能。

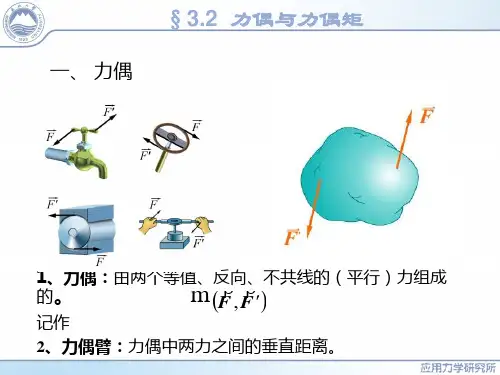
当我们双手紧握方向盘，驰骋在回家的路上，是多么幸福的一件事情啊！同学们可否知道，方向盘产生的转动效应是怎么产生的呢？这就是我们今天学习的知识点——力偶。

力偶是由大小相等、方向相反、作用线平行的两个力组成的力系组成的，记作(F,F')。

仅只有力偶组成的力系，只能使物体产生转动效应而不能使物体产生移动。

如下图，力偶中两力所在的平面，叫做力偶作用面；
两力作用线之间的垂直距离，叫做力偶臂，计为字母d。

力偶有两个重要的性质：
① 力偶没有合力，即对物体不产生移动效应。

② 力偶在任意坐标轴上的投影等于零，如下列图所示。

力偶对物体的转动效应，用力偶矩度量，以M〔F,F'〕或M 表示，
即
力偶矩是一个代数量，其绝对值等于一边力的大小与力偶臂的乘积，正负号表示力偶的转向，即，逆时针转为正，顺时针转为负，单位为
力偶矩是平面力偶作用的唯一度量。

力偶矩的性质
力偶矩的性质如下列图所示，力偶对任意点取矩都等于力偶矩，与矩心位置无关。

最后，结合下面两张图片，解释一下力偶矩的1个定理及2个推论，该定理和推论，只适用刚体，不适于变形体。

定理：在同一平面内的两个力偶，如果他们的力偶矩的大小相等，而且转向相同，那么此两力偶等效。

推论 1 力偶可以在其作用面内任意移转而不改变它对物体的转动效应；
推论 2 在保持力偶矩的大小和转向不变的条件下，可以任意改变力偶中力和力偶臂的大小而不改变力偶对物体的转动效应〔力偶的等效性〕。

好的，同学们，方向盘在你手中，转动原理在你心中，你掌握了吗？。

力矩和力偶从实践中知道，力除了能使物体移动外，还能使物体转动。

例如用扳手拧紧螺母时，加力可使扳手绕螺母中心转动，如图、所示。

一、力矩的概念图 扭矩扳手力矩表达的是力F 使扳手绕螺母中心O 转动的效应，转动中心O ，称为矩心，矩心到力作用线的垂直距离d ，称为力臂。

图用力的大小与力臂的乘积d F ⋅再加上正号或负号来表示力F 使物体绕O 点转动的效应，称为力F 对O 点的矩，简称力矩，用符号O M ()F 或O M 表示。

一般规定：使物体产生逆时针方向转动的力矩为正；反之，为负，所以力对点的矩是代数量。

即：()d F M O ⋅±=F （）力矩的单位为m kN m N ⋅⋅或。

例 已知kN F F F F 84321====，求各力对A 点的矩。

如图所示。

F 3图1.12图解：()()()()m kN l F M M m kN l F M m kN l F M A A A A ⋅=⨯⨯===⋅-=⨯-=-=⋅-=⨯⨯-=-=9.13866.02860sin 0162885.02830sin 421 4321F F F F一压路机的碾子重20kN ，半径40r cm =，如图所示。

如用一通过其中心的水平力F 使此碾子越过高8h cm =的台阶，求此水平力的大小。

如果要使作用的力最小，问应向哪个方向用力？并求最小力min F 的值。

F minrFαABh习题2－8图二、合力矩定理如果力系n 21F 、、F F ⋅⋅⋅的合力为R 。

由于合力R 与力系等效，则合力对其作用面内任一点O 的矩等于力系中各分力对同一点的矩的代数和，即：())()(....)()(21F M F M F M F M M O n O O O O ∑=+++=R （）上式称为合力矩定理。

例 图所示每1m 长挡土墙所受土压力的合力为R ，它的大小kN R 150=，方向如图示。

求土压力R 使墙倾覆的力矩。

解：土压力R 可使挡土墙绕点A 倾覆,分解土压力R ，得到1F 和2F 使墙倾覆的力矩，即R 对A 点的力矩为：自己动手做RF1F 2b=1.5mh=4.5mh/3Ad30°图()()()mkNbFhFMMMAAA⋅=⨯-⨯=⋅-⋅=+=4.825.130sin1505.130cos15032121FFR荷载F=2021α=45 ,尺寸如图。