当前位置：文档之家 › 中级微观经济学课件-Chapter20 成本最小化

中级微观经济学课件-Chapter20 成本最小化

  • 格式：ppt
  • 大小：754.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

微观经济学第20章(范里安) 上财

微观经济学第20章(范里安) 上财

y’ output units?
x2* = y
min{4x1,x2} y’
x1*
x1
= y/4
A Perfect Complements Example of Cost
Minimization The firm’s production function is
y min{4x1, x2}
and the conditional input demands are
For the production function
y f (x1, x2 ) x11/ 3x22 / 3
the cheapest input bundle yielding y output
units is
x*1(w1, w2, y), x*2(w1, w2, y)
w2 2w1
2/ 3
1/
3
y
12
2/ 3
w11/ 3 w
2/ 2
3y
21/ 3
w11/ 3 w
2/ 2
3y
3
w1w 4
2 2
1/ 3
y.
六、A Perfect Complements Example of Cost Minimization
The firm’s production function is
y min{4x1, x2}.
y,
2w1 w2
1/3 y
.
So the firm’s total cost function is
c(w1, w2, y) w1x*1(w1, w2, y) w2x*2(w1, w2, y)
So the firm’s total cost function is

第20章-成本最小化

第20章-成本最小化

y (x*1)1/3(x*2 )2/3
w1 w2
y / x1 y / x2
(1 (2
/ /
3)(x*1 )2/3(x*2 )2/ 3)(x*1 )1/3(x*2 )1/
3 3
x*2 2x*1
.
成本最小化的道格拉斯例子
(a) y (x*1)1/3(x*2 )2/3
(b)
w1 w2
x*2 2x*1
等成本线
给定 w1 和 w2, c 的等成本线方程是
w1x1 w2x2 c
x2
w1 w2
x1
c w2
.
斜率是 - w1/w2.
等成本线
x2
c” w1x1+w2x2 c’ w1x1+w2x2
c’ < c” x1
成本最小化问题
给定产量y’，哪个投入组合使成本最小？ x2
f(x1,x2) y’ x1
如果一个公司的技术显示出常数规模回 报，则双倍它的产量水平从y’ 到2y’ ， 要求双倍的所有投入水平. 整个生产成本双倍. 平均生产成本不改变.
规模报酬递减和平均总成本
如果一个公司的技术显示出规模报酬递 减，则双倍它的产量水平从y’ 到2y’ ， 要求超过双倍的所有投入水平.
规模报酬递减和平均总成本
y 短期产量
x2
扩展线
y
长期成本是
c(y) w1x1 w2x2 c(y) w1x1 w2x2 c(y) w1x1 w2x2
y
x2
x2 x2
x1 x1 x1
x1
短期和长期总成本
y 短期产量
x2
扩展线
y
长期成本是
c(y) w1x1 w2x2 c(y) w1x1 w2x2 c(y) w1x1 w2x2

(精品) 微观经济学课件：成本最小化

(精品) 微观经济学课件：成本最小化

x2
4x1 = x2
产出为y’的最小成本 投入束位于何处？
x2* = y
x1* = y/4
min{4x1,x2} y’ x1
成本最小化的完全互补品的例子
厂商的生产函数为：
y min{4x1, x2}
条件要素需求函数为：
x*1( w1,
w2,
y)
y 4
且
x*2( w1, w 2, y) y.
成本最小化的完全互补品的例子
厂商的生产函数为：
y min{4x1, x2}
条件要素需求函数为：
x*1( w1,
w2,
y)
y 4
且
x*2( w1, w 2, y) y.
厂商的总成本函数为：
c( w1, w 2, y) w1x*1( w1, w 2, y)
w 2x*2 ( w1, w 2 , y)
成本最小化的完全互补品的例子
2/ 3
y
w
2
2w1 w2
1/ 3
y
12
2/ 3
w11/ 3 w
2/ 2
3y
21/ 3
w11/
3w
2/ 2
3y
3
w1w 4
2 2
1/ 3
y.
成本最小化的完全互补品的例子
厂商的生产函数为：
y min{4x1, x2}.
给定投入要素价格w1 和 w2 。 厂商对于要素1和2的条件需求为多少？ 厂商的中成本函数为什么？
)1/ 3
2w1 w2
x*1
2/3
2w1 w2
2/3
x*1.
成本最小化的柯布-道格拉斯例子
(a) y (x*1 )1/3(x*2 )2/3

中级微观成本最小化

中级微观成本最小化
短期要素需求函数与长期要素需求函数之间的 关系
如果厂商所选择的固定要素使用量恰好使长期 成本最小化，那么长期内使成本最小化的可变 要素使用量就是厂商短期内所选择的使用量。
x1(w1 , w2 , y) x1s[w1, w2 , x2 ( y), y]
22
示例：
厂商的生产函数为y＝ALαKβ。生产要素L 和K的价格分别为wL，wK。
4
成本最小化
构造拉格朗日函数求解:
wx ( y f ( x))
一阶条件：wi
f ( xi ) , i xi
1,, n
任取其中的两种投入,变化后可得：
f ( x) / xi wi f ( x) / x j w j
5
边际替代率等于要素价格比率
成本最小化
等成本线斜率等于等产量线斜率，即
y f (x1*, x2*)
s.t. f (x1, x 2) y
短期要素需求：x1 =x1s(w1,w2 ,x2 ,y),x2 =x2
19
长期成本与短期成本
长期成本函数 长期成本函数指在一切生产要素都可调整的情况
下，生产既定产量的最小成本。 长期成本函数数学表述为：
c( y) min w1x 1w2 x2 s.t. f (x1, x 2) y
成本曲线
思考： 一家厂商在两家工厂生产相同的产品。如果 第一家工厂的边际成本大于第二家工厂的边 际成本，在两个工厂边际成本递增的情况下， 这家厂商该如何减少成本并维持相同的产量？
39
成本曲线的移动
要素价格 技术进步 税收政策 学习效应
40
成本曲线的移动
当要素价格呈比例变动，成本也将呈比例 变动
3
成本最小化
一个厂商的成本最小化问题可表示为：

微观经济学@微观经济学成本最小化

微观经济学@微观经济学成本最小化

0
y1
y
14.5
长期成本曲线
长期平均成本 离散的工厂规模水平 三条曲线所代表的生产规模为SAC1<SAC2<SAC3
C SAC1 C1 SAC2
SAC3
0
y1
y11 y2 y21 y3
y
14.5
长期边际成本曲线
长期成本曲线
长期边际成本曲线是与在不同的产出水平上最优 生产规模相对应的短期边际成本曲线的连线。
14
成本最小化
成本最小化 规模报酬和成本函数 短期成本和长期成本
14.1 成本最小化
假定厂商使用两种投入生产一定量产出，成本最小 化问题可以表述为： 总成本函数
minc minw1 x1 w2 x2 s.t . y f ( x1 , x2 )
解这类成本最小化问题—即实现合宜的产量水平所 必需的最小成本——取决于w1,w2,和y的值，所以我们 把它计作c(w1,w2, y)，这一函数叫做成本函数。 成本函数c(w1,w2, y)度量的是指当要素价格为(w1,w2) 时，生产y单位产量的最小成本。
0
A
y’
y
14.4
短期成本曲线
四、边际成本与平均成本关系
由于MC曲线呈U型，可知AC曲 线、AVC曲线也必然呈U型； MC曲线与AC曲线相交于AC曲 线的最低点，与AVC曲线相交 于纵轴和AVC曲线的最低点。 在AC（AVC）曲线的下降段， MC曲线低于AC（AVC）曲线； 在AC（AVC）曲线的上升段， MC曲线高于AC（AVC）曲线； 对于产量变化的反应，边际 成本MC要比平均成本AC和平 均可变成本AVC敏感 MC曲线 的变动快于AC曲线和AVC曲线 的变动。

范里安中级微观经济学第六版中文课件20 21

范里安中级微观经济学第六版中文课件20 21
x 2*
x*1、 x*2是w1,w2, y ’的 函数，记为x*1(w1,w2, y ’), x*2(w1,w2, y ’)称 为有条件的要素需求函数 或派生的要素需求。
f(x1,x2) y’
x 1*
x1
例题1
1 2 生产函数为 y x1 / 3 x2 / 3 投入的价格分别为w1,w2，产量为y。 求各投入的有条件的要素需求函数。
20.1 成本最小化
由目标函数 w1 x1 w2 x2 c
w1 c x2 x1 w2 w2
当我们变换c的数值时可以得到一簇等成本线，一条等成本线 上的每一点都表示同样的成本c，较高的等成本线表示较高的 成本。
x2
Slopes = -w1/w2.
c” w1x1+w2x2
c’ w1x1+w2x2
y
1 ab
1 bw1 a a b a b x2 ( w1 , w2 , y ) ( ) y aw2
w1 a a b w2 a b b a 1 b C ( w1 , w2 , y ) (a b) ( ) ( ) y a b
20.2
显示成本最小化
假定我们考虑两组要素价格(w1t,w2t)和(w1s,w2s)，与 此相关的厂商的选择为(x1t,x2t)和(x1s,x2s) 。假定这组 选择中的每一种都生产同样的产量y。 一个寻求成本最小化的厂商（在产出不能变化时）， 其实际生产选择一定满足：
s 2
1x1 2 x2 0
这说明要素需求曲线有负的(或至少是零的)斜率。 如果x1是变化的，要素价格与对要素的需求一定反 方向变化。
20.3 规模报酬和成本函数
平均成本是生产y单位产量的单位成本。 平均成本函数为：

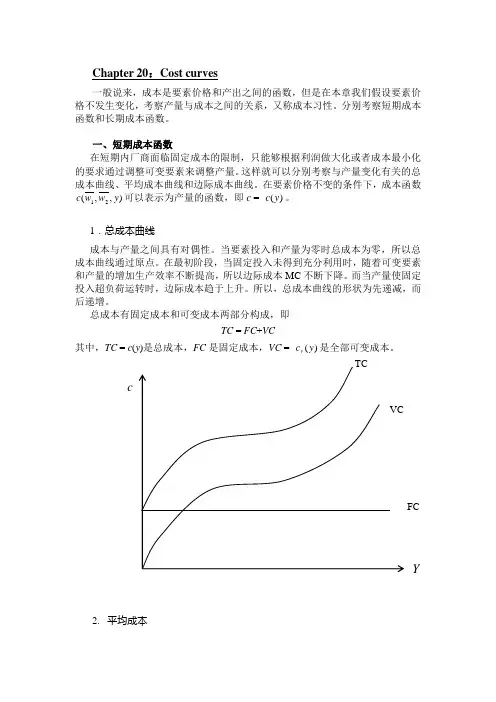
李荣林中级微观20

李荣林中级微观20

Chapter 20：Cost curves一般说来，成本是要素价格和产出之间的函数，但是在本章我们假设要素价格不发生变化，考察产量与成本之间的关系，又称成本习性。

分别考察短期成本函数和长期成本函数。

一、短期成本函数在短期内厂商面临固定成本的限制，只能够根据利润做大化或者成本最小化的要求通过调整可变要素来调整产量。

这样就可以分别考察与产量变化有关的总成本曲线、平均成本曲线和边际成本曲线。

在要素价格不变的条件下，成本函数),,(21y w w c 可以表示为产量的函数，即c = )(y c 。

1．总成本曲线成本与产量之间具有对偶性。

当要素投入和产量为零时总成本为零，所以总成本曲线通过原点。

在最初阶段，当固定投入未得到充分利用时，随着可变要素和产量的增加生产效率不断提高，所以边际成本MC 不断下降。

而当产量使固定投入超负荷运转时，边际成本趋于上升。

所以，总成本曲线的形状为先递减，而后递增。

总成本有固定成本和可变成本两部分构成，即TC = FC +VC其中，TC = c (y )是总成本，FC 是固定成本，VC = )(y c v 是全部可变成本。

cFCY2. 平均成本过原点做射线与总成本和可变成本曲线相交，交点的斜率就是在一定产量下的平均总成本AC (y )和平均可变成本AVC (y )。

平均可变成本位于平均总成本之下，两条直线之间的距离就是平均固定成本AFC (y )。

平均总成本可以用总成本曲线推导出来。

其形状为“U ”型。

)()()()(y AFC y AVC y FCy y c y y c AC V +=+==3. 边际成本过总成本曲线上的每一点作切线，其斜率就是对应的产出水平上的边际成本。

边际成本曲线也呈现“U ”型（图略）。

另外，对于成本函数FCy c y c v +=)()(来说，当y 变化时，FC 是不变的。

因此MC 可以用总成本函数来表示，也可以用可变成本函数来表示。

y y c y y c dy y dc y y c MC y y c y y c dy y dc y y c MC v v v v ∆-∆+==∆∆=∆-∆+==∆∆=)()()()()()()()(4. 平均成本曲线与边际成本曲线的相互关系在厂商的最优决策中，平均成本和边际成本之间的相互关系非常重要。

昆明理工大学MBA中级微观第20章讲义Cost Minimization

昆明理工大学MBA中级微观第20章讲义Cost Minimization

The Cost-Minimization Problem
The
levels x1*(w1,w2,y) and x1*(w1,w2,y) in the least-costly input bundle are the firm’s conditional demands for inputs 1 and 2 （条件要素需求）. The (smallest possible) total cost for producing y output units is therefore * c( w 1 , w 2 , y ) w 1x1 ( w 1 , w 2 , y ) * w 2x 2 ( w 1 , w 2 , y ).
y
y
Cond. demand for input 2
output expansion path
x* ( y ) 2 x* ( y ) 2 x* ( y ) 2 x* ( y ) x* ( y ) 1 1 x* ( y ) 1
y y
y x* ( y ) x* ( y ) x* 2 2 2 *
A Cobb-Douglas Example of Cost Minimization
At the input bundle (x1*,x2*) which minimizes the cost of producing y output units: (a) y ( x* )1/ 3 ( x* ) 2/ 3 and
2/ 3
y
is the firm’s conditional demand for input 2.
A Cobb-Douglas Example of Cost Minimization

中级微观经济第二十章 成本最小化

中级微观经济第二十章 成本最小化

w2 w1 2w 1 1 2
2/ 3
2/ 3
2w 1 y w2 w2
1/ 3
y
/ 3 2/ 3 1/ 3 1/ 3 2/ 3 w1 w y 2 w1 w 2 y 1 2
1/ 3 2 w 1w 2 3 y.
y
y
y y
x* 2 ( y ) x* 2 ( y ) x* 2 ( y )
* x* ( y ) 1 x1 ( y ) x* 1 ( y )
* * ( y ) x ( y ) x y x* 2 2 2 *
y y y
x 2 ( y )
x1 ,x 2 0
st
min w 1x1 w 2x 2
f ( x1 , x 2 ) y .
成本最小化问题
在最小成本投入束中的要素投入量
x1*(w1,w2,y) 和 x1*(w1,w2,y) 为厂商对于投 入要素1和2的条件需求函数。 生产y单位产出时的最小可能总成本为： * c( w 1 , w 2 , y ) w 1x1 ( w 1 , w 2 , y ) * w 2x 2 ( w 1 , w 2 , y ).
y y y
y x1
y y
要素1 的条件 需求
* * x* ( y ) x ( y ) x 1 1 1 * x1 ( y )
成本最小化的柯布-道格拉斯例子
对于生产函数：
产出为y的最小成本投入束为：
/ 3 2/ 3 y f ( x1 , x 2 ) x1 1 x2
x 2*
f(x1,x2) y’
x 1* x1
成本最小化问题
x2
一个内部成本最小化投入束满足： * * (a) f ( x1 , x 2 ) y 且 (b)等成本线= 等产量线的斜率

微观经济学第20章 成本最小化

微观经济学第20章 成本最小化

如果对每一种要素都要求使用一定的数量，
并且等产量线是一条非常光滑的曲线，那么成本
最小化的点就可以用相切条件来表征：等产量线
的斜率必定等于等成本线的斜率，即技术替代率
必定等于要素的价格比率：
MP1 TRS w1
MP2
w2
考虑当产量保持不变时，生产方式的任意
改变 (x1，x2 )。这种变化必定满足：
下的成本最小化选择；实现利润最大化的要素 需求则给出了既定产出品价格下的利润最大化 选择。
例子：特定技术下的成本最小化
完全互补生产技术
f x1, x2 min x1, x2
生产的产量为y时，最小生产成本为：
c w1, w2 , y w1 y w2 y w1 w2 y
完全替代的技术
素的价格保持不变，即△w2=0，那么：
w1x1 0
表明对要素1的需求必定减少，因此，有条 件的要素需求曲线必定是向下倾斜的。
三、规模报酬和成本函数 1．规模报酬不变 生产1单位产量的成本最小化问题，得单位
成本函数c（w1，w2，1）。生产y单位产量的最 小成本恰好是c（w1，w2，1）y，即在规模报酬
不变的情况下，成本是产量的线性函数。
2．规模报酬递增 规模报酬递增的条件下，成本的增长幅度 小于产量的增长幅度。如果厂商决定使产量翻 番，只要要素的价格保持不变，那么厂商的成 本增长小于1倍就可以得到这些产量。每种要素 增加小于1倍就会使成本增加也小于1倍，即成 本函数的增长线性地小于产量增长。 3．规模报酬递减 类似于规模报酬递增，有：成本函数的增 长线性地大于产量增长。
f x1, x2 x1 x2
生产的产量为y时，最小生产成本为：
c w1, w2, y min w1 y, w2 y y min w1, w2

20 成本最小化(2013)解析

20 成本最小化(2013)解析

2w 1 * 1/ 3 2 w 1 * * y ( x1 ) x1 x 1. w2 w2 2/ 3 w2 * 所以 x1 y 是厂商对于投入要素1的 2w 1
2/ 3
2/ 3
条件需求函数。
成本最小化 Cobb-Douglas 的例子
x2
在一个成本最小化的内点解上： * , x (a) f ( x* 1 2 ) y 且 (b) 等成本线的斜率等于等产量线的 斜率即
* 1 * 2
x 2* x 1*
w1 MP1 在 ( x , x )， TRS w2 MP2
f(x1,x2) y’
x1
min w1 x1 w2 x2 x1 , x2 s.t. f ( x1 , x2 ) y 建立拉格朗日函数: L w1 x1 w2 x2 ( f ( x1 , x2 ) y ) 对x1 , x2 , 求导, 得到一阶条件: f ( x1 , x2 ) w1 0 x1 f ( x1 , x2 ) w2 0 x2 f ( x1 , x2 ) y 0 整理, 并用第一个方程除以第 二个方程, 就可以得到: w1 f ( x1 , x2 ) / x1 w2 f ( x1 , x2 ) / x2
对x1 , x2 , 求导, 得到一阶条件:
a 1 b w1 ax1 x2 b 1 w2 bx1a x2 b x1a x2 y
第一个方程乘以 x1 , 第二个方程乘以 x2 , 就可以得到:
b w1 x1 ax1a x2 ay b w2 x2 bx1a x2 by
成本最小化：C-D技术的例子
* 1/ 3 * 2 / 3 (a) y ( x 1 ) ( x 2 )

钟根元《中级微观经济学学习指南》(第4版)练习题详解-第20~26章【圣才出品】

钟根元《中级微观经济学学习指南》(第4版)练习题详解-第20~26章【圣才出品】

第20章成本最小化一、判断题1．准不变成本是指长期中仅当产出量为零时才可以避免的成本。

（）【答案】T【解析】根据长期的定义，长期内不存在不变成本，但在长期内很容易产生准不变成本。

如果厂商在生产前必须支付一定数量的货币，准不变成本就产生了。

所以，准不变成本是长期中仅当产出量为零时才可以避免的成本。

2．如果规模报酬递增，那么平均成本是产出的递减函数。

（）【答案】T【解析】当规模报酬递增时，成本的增长幅度小于产量的增长幅度，因此，随着产量增加，平均成本趋于下降。

也就是说，平均成本是产出的递减函数。

3．如果规模报酬递减，那么沿着一条等成本线向右下方移动，平均成本有可能下降。

（）【答案】T【解析】当沿着一条等成本线向右下方移动时，产量有可能上升，而成本不变，所以平均成本可能下降。

如图20-1所示，图中有1条等成本线AB和3条等产量线Q1、Q2、Q3，且Q1＜Q2＜Q3。

当沿着等成本线AB由a点移动到E点时，产量Q1增加到Q2，而成本不变，所以平均成本下降了。

图20-1等成本线与等产量线4．某竞争性厂商生产函数为f（x1，x2）＝min{x1，x2}，则该厂商成本函数为c（w1，w2）＝min{w1，w2}×y。

（）【答案】F【解析】设y＝f（x1，x2），生产要素x1、x2价格分别为w1、w2。

由生产函数可知，生产要素x1、x2完全互补，理性厂商要素使用量满足y＝x1＝x2，则厂商成本函数为c（w1，w2，y）＝（w1＋w2）×y。

5．要素1的条件需求函数x1（w1，w2，y）是指厂商进行最佳要素选择时价格和产出之比的函数。

（）【答案】F【解析】有条件的要素需求给出的是既定产量水平下的成本最小化选择。

条件需求函数度量的是，在厂商生产某个既定产量y的条件下，价格、产量以及厂商的最优要素选择之间的关系。

6．如果两种元素的投入量相同，那么成本函数c（w1，w2，y）表示生产y单位产品的单位成本。

成本最小化范里安微观经济

成本最小化范里安微观经济
假设有两组要素价格 (w1t , w2t )和 (w1s , w2s )， 与此相关的厂商的选择为 (x1t , x2t和) (x1s , x2s )
假定上述两种选择都生产同样的产量y,如果
每种选择都属于成本最小化的选择，则有：
当前您正浏览第二十九页，共五十四页。
w1t x1t w2t x2t w1t x1s w2t x2s
x2
长期产量扩展曲线
c(y) w1x1 w2x2
x2 x2
c(y) w1x1 w2x2 y’’’ c(y ) w1x1 w2x2
x2
y’’
y’
x1 x1 x1
x1
当前您正浏览第五十页，共五十四页。
短期成本
x2
短期产量扩展曲线
x2 x2 x2
x1 x1 x1
y’’’
y’’ y’
c(w1, w2 , y) min w1 y, w2 y
minw1, w2 y
当前您正浏览第二十七页，共五十四页。
柯布－道格拉斯技术
f
( x1 ,
x2 )
Ax1a x
b 2
其成本函数为：
a
b
1
c(w1,
w2
,
y)
kw1ab
wab 2
y
ab
当前您正浏览第二十八页，共五十四页。
19.2 显示的成本最小化
长期要素需要函数为：
x1* x1* (w1, w2 , y) x2* x2* (w1, w2 , y)
长期成本函数为：
cs ( y) w1x1(w1, w2, y) w2x2 (w1, w2, y)
当前您正浏览第四十六页，共五十四页。
短期成本函数与长期成本函数的关系
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
c(w1, w2, y) = w1x1*(w1, w2, y) + w2x2* (w1, w2, y).
2020/11/8
中级微观经济学
14
成本最小化问题
给定w1, w2 和 y, 如何确定最小成本的投入 组合1、2的位置？ 厂商的总成本函数如何计量?
比较消费者理论中的消费者最优选择问题！
（第5章）
11
成本最小化问题 （The Cost-Minimization Problem）
考虑用两种要素生产一种产品的厂商。 厂商的生产函数为
y = f(x1,x2). 其中 y 0是给定的。 假定投入品价格 w1 、 w2 是给定的。则投 入组合的成本为w1x1 + w2x2.
2020/11/8
中级微观经济学
2020/11/8
中级微观经济学
29
成本最小化
Cobb-Douglas 的例子
一个具有 Cobb-Douglas 生产技术厂商的生 产函数为
y f (x1, x2 ) x11/3x22/3.
厂商面临给定的要素价格 w1 、 w2。 厂商的有条件的要素需求函数是什么?
2020/11/8
中级微观经济学
w2 x2.
一阶条件是：
p
f
( x1*, x1
x2 *)
w1
0.
p
f
(x1*, x2*) x2
w2
0.
2020/11/8
中级微观经济学
5
对于C-D函数 f (x1, x2 ) x1a x2b
利润最大化问题是：
max x1, x2
px1a x2b
w1x1
w2 x2
一阶条件是：
pax1a1x2b w1 0
2w1 w2
x*1
.
(b)
w1 w2
x*2 2x*1
.
2020/11/8
中级微观经济学
33
成本最小化：C-D技术的例子
(a) y (x*1)1/3(x*2 )2/3
由(b)可得,
x*2
2w1 w2
x*1
.
(b)
w1 w2
x*2 2x*1
.
代入(a)得：
y
(x*1
)1/
3
2w1 w2
x*1
2/3
c” w1x1+w2x2
c’ w1x1+w2x2
c’ < c”
x1
2020/11/8
中级微观经济学
19
等产量线
x2
所有产出为y’ 的投入要素的集合。 哪一个最便宜？
2020/11/8
f(x1,x2) y’ x1
中级微观经济学
20
成本最小化问题
x2
所有产出为y’ 的投入要素的集合。 哪一个最便宜？
30
成本最小化 Cobb-Douglas 的例子
生产给定产量成本最小化的投入要素组合 (x1*,x2*) 满足
(a) y (x*1)1/3(x*2 )2/3
(b)
w1 w2
y y
/ /
x1 x2
(1 / 3)(x*1 )2/3(x*2 )2/3 (2 / 3)(x*1)1/3(x*2 )1/3
所以
x*1
2ww21
2/
3
y
是厂商对于投入要素1的
条件需求函数。
2020/11/8
中级微观经济学
35
成本最小化 Cobb-Douglas 的例子
由于 且
x*2
2w1 w2
x*1
x*1
w2 2w1
2/3
y
则
x*2
2w1 w2
w2 2w1
2/ 3
y
2w1 w2
1/ 3
y
是厂商对于投入要素2的条件需求函数。
L w1x1 w2 x2 ( f (x1, x2 ) y)
对x1, x2 , 求导, 得到一阶条件:
w1
f
( x1 , x1
x2 )
0
w2
f
(x1, x2 ) x2
0
f (x1, x2 ) y 0
整理,并用第一个方程除以第二个方程, 就可以得到:
w1 f (x1, x2 ) / x1 w2 f (x1, x2 ) / x2
x*2
y y
2020/11/8
x*1(y) x*1(y)
x1
x*1 ( y )
中级微观经济学
x*1(y) x*1(y) x*1 ( y )
x*1
42
要素的条件需求曲线
x2 w1 、 w2不变
yy 投入 2的条件需求
y
x*2
y y
y y
y
2020/11/8
x*1(y) x*1(y)
x1
x*1 ( y )
中级微观经济学
x*1(y) x*1(y) x*1 ( y )
x*1
41
要素的条件需求曲线
x2 w1 、 w2不变
yy
y
y
y
x*2 ( y ) x*2 ( y ) x*2 ( y )
产出扩展线
y y
y
yy
y
x*2(y) x*2(y) x*2 ( y )
yy x*2(y)
x*2
y
y y
y
2020/11/8
x*1(y) x*1(y)
x1
x*1 ( y )
中级微观经济学
x*1 ( y )
x*1
39
要素的条件需求曲线
x2 w1 、 w2不变
yy
y
y
x*2 ( y ) x*2 ( y ) x*2 ( y )
yy x*2(y)
x*2 ( y )
x*2
y y
(b) 等成本线的斜率等于等产量线的斜率
即
在( x1*,
x2* )，
w1 w2
TRS
MP1 MP2
x2*
f(x1,x2) y’
x1*
x1
2020/11/8
中级微观经济学
27
成本最小化问题
相切条件的推导方法）： 1、直接代入法 2、拉格朗日法
2020/11/8
中级微观经济学
28
min x1, x2 w1x1 w2 x2 s.t. f (x1, x2 ) y 建立拉格朗日函数:
2020/11/8
f(x1,x2) y’ x1
中级微观经济学
21
成本最小化问题
x2
所有产出为y’ 的投入要素的集合。 哪一个最便宜？
2020/11/8
f(x1,x2) y’ x1
中级微观经济学
22
成本最小化问题
x2
所有产出为y’ 的投入要素的集合。 哪一个最便宜？
2020/11/8
f(x1,x2) y’ x1
1/3 y
.
2020/11/8
中级微观经济学
37
要素的条件需求曲线
（Conditional Input Demand Curves） x2 w1 、 w2不变
y y
y
x1
2020/11/8
中级微观经济学
38
要素的条件需求曲线
x2 w1 、 w2不变
y
y
x*2 ( y ) x*2 ( y ) x*2 ( y )
w1x1 w2x2 c
重新排列得到
x2
w1 w2
x1
c w2
.
等成本线的斜率为- w1/w2,,纵截距为c/w2.
2020/11/8
中级微观经济学
17
等成本线
x2
c” w1x1+w2x2 c’ w1x1+w2x2
c’ < c”
x1
2020/11/8
中级微观经济学
18
等成本线
x2
斜率 = -w1/w2.
x*2 2x*1
.
2020/11/8
中级微观经济学
31
成本最小化：C-D技术的例子
(a) y (x*1)1/3(x*2 )2/3
(b)
w1 w2
x*2 2x*1
.
2020/11/8
中级微观经济学
32
成本最小化：C-D技术的例子
(a) y (x*1)1/3(x*2 )2/3
由(b)可得,
x*2
中级微观经济学
23
成本最小化问题
x2
所有产出为y’ 的投入要素的集合。 哪一个最便宜？
x2* x1*
f(x1,x2) y’ x1
2020/11/8
中级微观经济学
24
成本最小化问题
x2
在一个成本最小化的内点解上： (a) f (x*1, x*2 ) y
x2* x1*
f(x1,x2) y’ x1
2020/11/8
中级微观经济学
25
成本最小化问题
x2
在一个成本最小化的内点解上： (a) f (x*1, x*2 ) y 且
(b) 等成本线的斜率等于等产量线的斜率
x2* x1*
f(x1,x2) y’ x1
2020/11/8
中级微观经济学
26
成本最小化问题
x2
在一个成本最小化的内点解上： (a) f (x*1, x*2 ) y 且
20 成本最小化
Cost Minimization
2020/11/8
中级微观经济学
1
本章要点
成本最小化 规模报酬和成本函数 长期成本和短期成本
关键词：成本函数
2020/11/8