数学建模疾病的确诊

我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D 中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：广东商学院参赛队员（打印并签名）：1. 邓思文2. 苏境财3. 吴妙指导教师或指导教师组负责人（打印并签名）：戴宏亮日期：2012 年8 月18 日赛区评阅编号（由赛区组委会评阅前进行编号）2010 高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：疾病诊断问题摘要随着就医压力增加，在降低误诊率的前提下提高诊断效率是非常重要的，本文利用确诊样本数据建立判别模型，并利用模型筛选出主要元素，对就诊人员进行诊断。

针对问题（1），利用确诊数据建立Fisher判别模型、Logistic 回归模型和BP神经网络模型，运用matlab、spss求解，定出判别标准，并进行显著性检验和回代检验，判别模型的准确率。

结果显示Fisher 判别模型的准确率为%，Logistic回归模型和BP神经网络模型准确率均为100%，Logistic 回归模型相对简便。

针对问题（2），选择问题一中检验准确率为100%的Logistic 回归模型和BP神经网络模型对40 名就诊人员进行诊断，结果如下表：针对问题（3），建立Logistic 逐步回归模型对元素进行筛选，利用spss 软件求解，确定Ca和Fe 是影响人们患这种病的主要因素，因此在建立诊断模型时，其他元素不作为参考指标。

数学建模与优化算法在医疗诊断与预测中的应用随着医学技术的不断发展，数学建模与优化算法在医疗领域的应用越来越广泛。

通过数学建模，我们可以更好地理解医学问题的本质，并通过优化算法找到最佳的解决方案。

本文将重点介绍数学建模与优化算法在医疗诊断与预测中的应用。

首先，数学建模与优化算法可以帮助医生提高疾病的诊断准确性。

在医疗诊断中，医生需要根据患者的症状、体征和检查结果来做出准确的诊断。

然而，由于疾病症状的复杂性和多样性，医生常常会面临诊断错误的情况。

通过数学建模，我们可以将症状、体征和检查结果等相关信息转化为数学模型，然后通过优化算法来找到最优的诊断结果。

例如，可以使用统计学方法建立疾病预测模型，然后通过机器学习算法进行训练和优化，从而通过患者的症状和体征来预测其可能的疾病。

这样一来，医生可以通过数学模型和优化算法的辅助，提高诊断准确性，减少误诊率。

其次，数学建模与优化算法还可以用于医学图像分析和识别。

在医学领域中，医学影像图像的分析和识别对于疾病诊断和治疗起着重要的作用。

然而，由于医学图像的复杂性和多样性，医生在分析和识别时往往面临一定的挑战。

通过数学建模，我们可以将医学图像转化为数学模型，并通过优化算法对其进行分析和识别。

例如，可以使用计算机视觉和图像处理技术构建医学图像分析模型，然后通过优化算法对医学图像进行特征提取和分类，从而实现医学图像的自动分析和识别。

这样一来，医生可以通过数学模型和优化算法的辅助，提高医学图像分析和识别的准确性和效率。

另外，数学建模与优化算法还可以帮助医生预测疾病的发展和转化。

在医疗领域中，预测疾病的发展和转化对于疾病管理和治疗起着重要的作用。

通过数学建模，我们可以将患者的病历数据、生理指标等信息转化为数学模型，并通过优化算法对其进行分析和预测。

例如，可以使用时间序列分析和机器学习算法建立疾病发展预测模型，然后通过优化算法进行模型训练和优化，从而预测患者疾病的发展趋势和转化概率。

利用数学建模及算法研究肺癌早期诊断问题肺癌早期诊断一直以来都是医学领域的热点问题之一。

然而，由于肺癌的发展具有隐匿性和突然性的特点，常常导致在早期阶段难以及时发现和诊断。

为了解决这一问题，数学建模及算法的应用在肺癌早期诊断中发挥了重要作用。

一、数学建模在肺癌早期诊断中的应用肺癌的早期诊断主要依靠肺部CT、胸部X射线等影像学技术。

然而，仅凭肿瘤的外观特征往往不能准确判断肿瘤的恶性程度和发展趋势。

因此，数学建模成为一种有效的辅助手段。

1.肺癌风险评估模型通过收集大量患者的临床数据，如年龄、性别、吸烟史、家族病史等，构建一种肺癌风险评估模型，可以预测患者发生肺癌的概率。

这种模型能够帮助医生识别高危人群，及早进行进一步检查和筛查，提高早期诊断的准确性。

2.肺癌图像分析肺癌的早期病灶往往较小且形状不规则，传统的人工分析方法容易漏诊和误诊。

数学建模可以通过计算机视觉和图像处理技术，自动提取肺癌影像特征，如肿瘤的大小、形状、纹理等，通过建立数学模型进行分类和诊断。

3.肺癌生长模型通过采集患者肺癌的多次CT图像，建立肺癌生长模型，可以预测肿瘤的生长速度和趋势。

这一模型可以帮助医生评估肿瘤的恶性程度，制定更合适的治疗方案。

二、算法在肺癌早期诊断中的应用随着人工智能和机器学习算法的发展，其在肺癌早期诊断中的应用也日益普及。

算法通过对大量数据的分析和学习，能够识别肺癌的特征和模式，提高诊断的准确性和效率。

1.机器学习算法机器学习算法主要包括监督学习和无监督学习两种方式。

在肺癌早期诊断中，可以通过监督学习的方法，利用已有的肺癌患者数据和正常人群数据建立分类模型，以实现对新患者肺癌的自动诊断。

无监督学习则可发现隐藏在数据中的模式，帮助医生进一步研究肺癌的发展规律。

2.深度学习算法深度学习算法是一种基于神经网络的算法，可以自动从大量样本中学习和识别特征。

在肺癌早期诊断中，深度学习算法可以通过对肺部CT图像的分析，提取出更多肿瘤的特征信息，从而提高诊断的精确性。

心脏病的判别
问题背景
心脏是维持全身血液循环的最重要器官。

由于现代人不正确的饮食和运动习惯等因素，心脏病患者人数逐年上升，心脏病已经成为威胁人类生命的十大疾病之一，除了老年人，中青年也成为心脏病猝死的高危人群。

年轻人的心脏病突发往往没有明显先兆，突然发作时很危险，心脏病的病因很多，有时很难判断一个人是否患有心脏病。

问题数据
附录二是到某医院做心脏病检测的一些确诊者的生理指标数据。

（指标A，B,…M的含义见附录一，指标N表示是否确诊为心脏病以及患病的程度）
需解决问题
问题一：根据附录二中的数据，提出判别心脏病以及患病程度的方法，并检验你提出方法的正确性。

问题二：按照问题一提出的方法，判断附录三中的44名就诊人员的患病情况。

问题三：能否根据附录二的数据特征，确定哪些指标是影响人们患心脏病的关键或主因素，以便减少化验的指标。

问题四：根据问题三的结果，重复问题二的工作，并与问题二的结果对比作进一步分析。

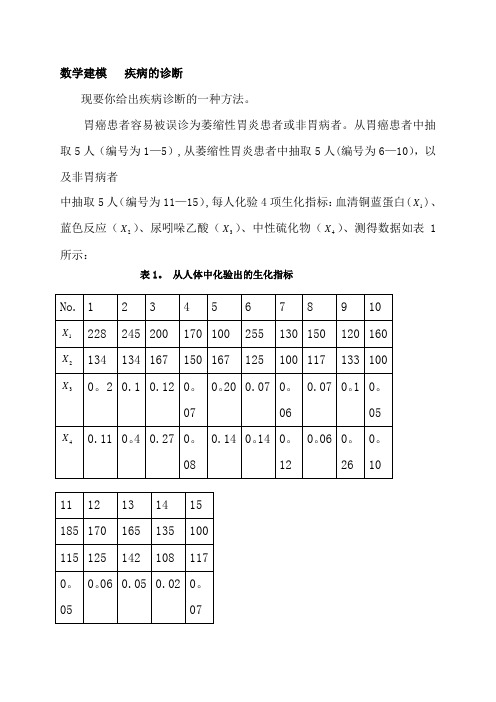
数学建模疾病的诊断现要你给出疾病诊断的一种方法。

胃癌患者容易被误诊为萎缩性胃炎患者或非胃病者。

从胃癌患者中抽取5人（编号为1-5），从萎缩性胃炎患者中抽取5人（编号为6-10），以及非胃病者中抽取5人（编号为11-15），每人化验4项生化指标：血清铜蓝蛋白（X）、1蓝色反应（X）、尿吲哚乙酸（3X）、中性硫化物（4X）、测得数据如表1 2所示：表1. 从人体中化验出的生化指标根据数据，试给出鉴别胃病的方法。

论文题目：胃病的诊断摘要在临床医学中，诊断试验是一种诊断疾病的重要方法。

好的诊断试验方法将对临床诊断的正确性和疾病的治疗效果起重要影响。

因此，对于不同疾病不断发现新的诊断试验方法是医学进步的重要标志。

传统的诊断试验方法有生化检测、DNA检测和影像检测等方法。

而本文则通过利用多元统计分析中的判别分析及SPSS软件的辅助较好地解决了临床医学中胃病鉴别的问题。

在临床医学上，既提高了临床诊断的正确性，又对疾病的治疗效果起了重要效果，同时也减轻了病人的负担。

判别分析是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。

其基本原理是按照一定的判别准则，建立一个或多个判别函数，用研究对象的大量资料确定判别函数中的待定系数，并计算判别指标。

首先，由判别分析定义可知，只有当多个总体的特征具有显著的差异时，进行判别分析才有意义，且总体间差异越大，才会使误判率越小。

因此在进行判别分析时，有必要对总体多元变量的均值进行是否不等的显著性检验。

其次，利用判别分析中的费歇判别和贝叶斯判别进行判别函数的建立。

最后，利用所建立的判别函数进行回判并测得其误判率，以及对其修正。

本文利用SPSS软件实现了对总体间给类变量的均值是否不等的显著性检验并根据样本建立了相应的费歇判别函数和贝叶斯判别函数，最后进行了回判并测得了误判率，从而获得了在临床诊断中模型，给临床上的诊断试验提供了新方法和新建议。

肾炎的诊断摘要本文研究的问题是通过检测人体内各种元素的含量，来诊断就诊人员是否患有肾炎。

我们首先将健康的和患病的人群的体内的相关元素的平均值用∑====B 301)0,1;7,...,2,1(301i ij iy y i x 计算出来,发现体内的元素含量的确和患病有必然的联系。

我们再利用Excel 软件中的logistic 模型对样本做了具体的分析。

( logistic 模型被广泛应用于病理学中,被作为病理学研究的常用模型) 发现各元素的含量与是否患有肾炎之间的确有一定关联，属于线性回归问题。

接着,计算出该线性方程的常量和系数从而完成模型的初步建立。

对于问题一，我们取1-60号为样本，建立线性回归模型，ii ii x b x b x b b x b x b x b b e e p +++++++++= (22110221101)以各元素的含量(1,2,3,4,5,6,7)i x i =为自变量，是否患有肾炎为因变量，用y 表示，当1y =时，表示患有肾炎；当0y =时，表示健康。

然后利用回归统计表、方差分析表、回归参数表中的数据进行分析，来衡量线性回归的拟合度，以及线性方程中各参数的显著性，发现其回归程度较好。

对60例受检者的数据进行判别，若p 大于0.5则判定为患病，若小于0.5则判定为健康。

结果正确率为93.33%。

对于问题二，我们利用问题一中建立的优化模型进行检验，将待诊断的30个病例中各元素的含量代入模型一中，计算出对应的p 值，然后和0.5进行比较，通过对数据分析处理：检验出61、62、64、65、66、68、69、71、72、73、75、76、79、83、85 号就诊人员患有肾炎；63、67、70、74、77、78、80、81、82、84、86、87、88、89、90 号就诊人员是健康的。

对于问题三，由问题一知,这七种元素的回归系数显著性由高到低顺序依次为Ca,Cu,Fe,Mg,Na,Zn,K 。

诊断疾病问题数学建模目录一、摘要---------------------------------------------- （1）二、问题重述---------------------------------------------- （1）三、问题分析---------------------------------------------- （2）四、问题假设---------------------------------------------- （2）五、符号说明---------------------------------------------- （2）六、模型建立与求解---------------------------------------------- （2）七、模型分析---------------------------------------------- （7）八、模型评价---------------------------------------------- （7）九、模型推广---------------------------------------------- （8）十、附录---------------------------------------------- （8）十一、参考文献---------------------------------------------- （11）小组成员：姓名年级与专业胡阿娟09级数学与应用数学1班刘琳09级数学与应用数学1班王慧09级数学与应用数学2班摘要本文研究的问题是通过研究人体内各元素含量，来诊断就诊人员是否患有胃病。

我们利用Excel 软件对样本数据进行了统计分析，发现各元素的含量于是否又有胃病有一定的关联，属于线性回归问题。

我们取1—3号、6—8号、11—13号病例为样本，建立线性回归模型，以各元素的含量x1、x2、x3、x4为自变量；是否患有胃病为因变量，用y 表示，当y=2时，表示患有胃癌；当y=1时，表示患有萎缩性胃炎；当y=0时，表示健康。

医学肾炎化验分析模型摘要此数学模型的建立主要是为了解决这样的问题，通过检测人体内相关微量元素的含量来判定一个人是否患肾炎。

因而在此数学模型中，自变量为体内若干种微量元素的含量，因变量作为判定一个人是否患病的主要数据，做如下设定，当被确诊为患病时，设为1，被确诊为健康时，设为0.我们通过对数据的基本分析和判别，试图通过线性回归模型解决这个问题，经过查阅相关资料，了解到logistic模型被广泛应用于病理学研究中作为研究模型，于是利用excel中的回归工具建立logistic回归模型，计算出该线性方程的常量和系数从而完成模型的初步建立。

然后利用回归统计表、方差分析表中、回归参数表等中的数据进行分析，来衡量线性回归的拟合度，以及线性方程中各参数的显著性，发现其回归程度较好，又通过将表1和表2中已确诊的数据代入，对60例受检者的数据进行判别，若大于0.5则判定为患病，若小于0.5则判定为健康。

对应的logit（p/（1-p））为正数时候患病,为负数时为健康。

发现该模型在本题判断中的正确率高达93.33%，预测能力显著。

诊断待测病人，将表3中的数据代入计算其患病概率，判别标准同上所述，得出受检者中有15人健康，15人患病的结论。

回归参数表中回归系数的统计量的线性系数显著性t值，表征了该系数的显著性水平，也表征了该项因素对于因变量判定的影响程度。

因此以此为衡量的标准来筛选7项相关因素，找到系数显著性最小三种元素，分别为Na,Zn,K；我们又用排列组合的方法分别删除其中的一种、两种和三种元素，分别计算此时代入前60组数据时的准确度，通过比较从而确定主要影响元素。

保留了Ca,Cu,Fe,Mg四种元素，除去非主因素的干扰，用同样的方法重新计算该模型各系数的数值，在保证较高准确率的前提下，最终达到了简化检测过程的目的。

利用排除非显著性元素后的Logistic模型，将表3中的数据代入计算其患病概率，判别标准同上所述，得出受检者中有16人健康，14人患病的结论。

数学建模在医疗诊断辅助决策中的应用及效果评价随着科技的不断发展，计算机技术和数学建模在医疗诊断和决策辅助方面的应用也越来越受到重视。

数学建模的应用可以帮助医生更准确地进行诊断，提高患者的治疗效果，减少误诊率，本文将重点探讨数学建模在医疗诊断辅助决策中的应用及其效果评价。

一、数学建模在医疗诊断中的应用1. 数据分析和预测数学建模可以对大量的医疗数据进行分析和挖掘，帮助医生了解病情的发展趋势，并预测可能的治疗结果。

通过分析患者的病史、生理指标、影像学等数据，数学模型能够提供患者的风险评估和预后预测，帮助医生制定更合理和个性化的治疗方案。

2. 图像处理和识别数学建模在医疗影像领域的应用也非常广泛。

通过图像处理和识别技术，可以对医学图像进行分析，帮助医生快速准确地发现异常病变。

例如，基于数学模型的计算机辅助诊断系统能够对医学影像进行自动分析和解读，辅助医生进行判断和决策。

3. 疾病模型和模拟通过建立数学模型和仿真，可以模拟疾病的发展过程和治疗效果，并帮助医生更全面地了解疾病的本质和机制。

例如，在肿瘤的研究中，数学模型能够根据肿瘤细胞的生长、扩散和治疗效果等参数，预测肿瘤的生长速度、治疗效果和预后等重要指标。

二、数学建模在医疗诊断中的效果评价1. 正确率和灵敏度使用数学建模进行医疗诊断辅助决策时，评估模型的基本指标之一是正确率和灵敏度。

正确率指的是模型给出的诊断结果与实际诊断结果一致的比例，而灵敏度则衡量了模型对疾病的敏感性，即能够正确地识别出患者的病情。

2. 误诊率和特异度另一个重要的评价指标是误诊率和特异度。

误诊率指的是模型将健康人误诊为病人的比例，而特异度则衡量了模型对疾病的特异性，即能够正确地判断出健康人。

3. ROC曲线和AUC值ROC曲线和AUC值是评估模型性能的常用指标。

ROC曲线是以真阳性率（TPR）为纵轴、假阳性率（FPR）为横轴绘制的曲线，用于衡量模型的敏感性和特异性。

AUC值则是ROC曲线下的面积，通常用来评估模型的综合性能，AUC值越接近1，说明模型的性能越好。

化验结果诊断的数学模型摘要本文就健康人和某病患者体内Zn、Cu、Fe、Ca、Mg、K、Na七种元素含量的不同，建立相应数学模型来判断任一一个就诊人员是否为患病者。

对于问题一，我们采用费歇尔判别模型。

利用表1确诊病例的化验结果（其中1-30号为确诊患者和31-60号为健康人）中的全部数据建立费歇尔模型，形成简单的判别方法；之后用表1中的数据对该模型进行检验，继而对该模型的正确性做出判断。

通过检验我们发现，该模型具有很高的可信度，正确率达95%，可以作为一种简便的判别方法。

对于问题二，我们利用问题一中提出的方法对表2中15名就诊人员的化验结果进行了判别，判别结果为61、62、63、64、66、67、68、71、75共9位就诊人员为患病，其他就诊人员为健康。

对于问题三，我们采用主成分分析法再次对表1中的60组数据进行分析，确定影响该病诊断的主要因素为Zn、Ca、Mg、K四种元素。

重复解决问题二，其结果与问题一中建立费歇尔模型的判定结果相一致。

关键词：化验结果诊断费歇尔判别模型主成分分析法回判一、问题重述日常生活中，到医院诊断时通常要检验各种元素的含量，根据各项指标的含量是否异常来判断是否患有某种疾病。

表1中1-30号为确诊为患病的病例关于病例Zn、Cu、Fe，Ca、Mg、K、Na七种指标的化验结果，31-60是健康人相同的7中指标的化验结果。

依据题中所给的数据，我们要解决以下两个问题：问题一：根据表1中60名就诊人员的化验结果确定一种简单方法来判断就诊人员是否为该病炎患者，并对该判断方法进行检验看其是否正确。

问题二：依据问题一确定的判断方法对表2中15名就诊人员的化验结果进行判断，看其健康还是该病的患者。

问题三：依据表1的数据，确定对该疾病诊断有较大影响的元素。

二、问题分析针对问题一：主要根据表1中60名就诊病例的七个指标，找到一种简单判别方法来确定就诊人员是否患病。

由于每个个体七项指标的数据是相对独立的，因此我们采用了费歇尔模型，即借助方差分析思想构造一个判别函数（多元函数），再根据表1中60名病例的相关数据确定多元函数各元的系数；最后，我们采取回判法，进行模型正确性检验。

疾病诊断数学模型摘要本文解决的是如何根据就诊者体内各元素含量判别某人是否患有某种疾病和确定哪些指标是影响人们患该疾病的关键因素的问题。

通过分析可知此类问题为典型的分析判别，在此我们采用元素判别和Bayes 判别并应用Excel 和SAS 软件来对某人是否患病进行判别，并通过主成分分析法来确定患该疾病的关键因素。

对于问题一，我们采用元素判别和Bayes 判别进行前60人是否患病的判别，并对其结果进行对比。

对于元素判别，我们用Excel 对化验结果数据进行统计并通过折线图得出其分界值，然后与是否患病的真实情况进行对比，得出其准确度为95%；对于Bayes 判别，通过编写SAS 程序来进行判别，并得出其准确度为93.33%；考虑到诊断的实际情况和简便性最终确定Bayes 判别为本文所要使用的判别方法。

对于问题二，我们利用问题一中建立的判别模型对表2中的15名就诊人员的化验结果进行检验，检验结果为：9个人为患病者，6 个人为健康人员。

对于问题三，为了确定影响人们患该病的关键或主要因素，我们选取表1中的数据作为样本，建立主成分分析模型，通过对表1中的数据进行标准化并确定相关系数矩阵，接着，求出相关矩阵的特征值和特征向量，然后通过前m 个主成分的累计贡献率满足%8511≥∑∑==pk kik kλλ来确定主成分的个数，最后通过主成份载荷分析得出最能代表主成分的原指标即所要求的主要因素为Fe 、Ca 、Mg 、Cu 。

在此基础上，得到去掉K 、Na 、Zn 的化检结果的新样本，利用Bayes 判别，再对表2中的15名就诊人员的化验结果进行判别，判别结果：9个人为患病者，6 个人为健康人员。

关键词： 元素判别，Bayes 判别，主成分分析法，Excel ，SAS 软件一 问题重述.人们到医院就诊时，通常要化验一些指标来协助医生诊断。

一般初步判断某人是否患病是通过观察某人体内元素的含量。

通过题目给出数据可以看出，其中1－30号病例是已经确诊为病人的化验结果；31－60号病例是已经确诊为健康人的结果。

数学建模疾病的诊断现要你给出疾病诊断的一种方法。

胃癌患者容易被误诊为萎缩性胃炎患者或非胃病者。

从胃癌患者中抽取5人（编号为1—5）,从萎缩性胃炎患者中抽取5人(编号为6—10），以及非胃病者中抽取5人（编号为11—15）,每人化验4项生化指标：血清铜蓝蛋白(X)、1蓝色反应（X）、尿吲哚乙酸（3X）、中性硫化物（4X）、测得数据如表1 2所示：表1。

从人体中化验出的生化指标根据数据，试给出鉴别胃病的方法。

论文题目：胃病的诊断摘要在临床医学中，诊断试验是一种诊断疾病的重要方法。

好的诊断试验方法将对临床诊断的正确性和疾病的治疗效果起重要影响。

因此，对于不同疾病不断发现新的诊断试验方法是医学进步的重要标志。

传统的诊断试验方法有生化检测、DNA检测和影像检测等方法.而本文则通过利用多元统计分析中的判别分析及SPSS软件的辅助较好地解决了临床医学中胃病鉴别的问题。

在临床医学上，既提高了临床诊断的正确性，又对疾病的治疗效果起了重要效果，同时也减轻了病人的负担。

判别分析是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。

其基本原理是按照一定的判别准则，建立一个或多个判别函数,用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标。

首先，由判别分析定义可知,只有当多个总体的特征具有显著的差异时,进行判别分析才有意义，且总体间差异越大,才会使误判率越小.因此在进行判别分析时,有必要对总体多元变量的均值进行是否不等的显著性检验。

其次，利用判别分析中的费歇判别和贝叶斯判别进行判别函数的建立。

最后,利用所建立的判别函数进行回判并测得其误判率，以及对其修正。

本文利用SPSS软件实现了对总体间给类变量的均值是否不等的显著性检验并根据样本建立了相应的费歇判别函数和贝叶斯判别函数，最后进行了回判并测得了误判率，从而获得了在临床诊断中模型，给临床上的诊断试验提供了新方法和新建议.关键词:判别分析；判别函数；Fisher判别；Bayes判别一问题的提出在传统的胃病诊断中,胃癌患者容易被误诊为萎缩性胃炎患者或非胃病患者，为了提高医学上诊断的准确性，也为了减少因误诊而造成的病人死亡率，必须要找出一种最准确最有效的诊断方法。

数学建模疾病的诊断现要你给出疾病诊断的一种方法。

胃癌患者容易被误诊为萎缩性胃炎患者或非胃病者。

从胃癌患者中抽取5人（编号为1-5），从萎缩性胃炎患者中抽取5人（编号为6-10），以及非胃病者中抽取5人（编号为11-15），每人化验4项生化指标：血清铜蓝蛋白（X）、1蓝色反应（X）、尿吲哚乙酸（3X）、中性硫化物（4X）、测得数据如表1 2所示：表1. 从人体中化验出的生化指标根据数据，试给出鉴别胃病的方法。

论文题目：胃病的诊断摘要在临床医学中，诊断试验是一种诊断疾病的重要方法。

好的诊断试验方法将对临床诊断的正确性和疾病的治疗效果起重要影响。

因此，对于不同疾病不断发现新的诊断试验方法是医学进步的重要标志。

传统的诊断试验方法有生化检测、DNA检测和影像检测等方法。

而本文则通过利用多元统计分析中的判别分析及SPSS软件的辅助较好地解决了临床医学中胃病鉴别的问题。

在临床医学上，既提高了临床诊断的正确性，又对疾病的治疗效果起了重要效果，同时也减轻了病人的负担。

判别分析是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。

其基本原理是按照一定的判别准则，建立一个或多个判别函数，用研究对象的大量资料确定判别函数中的待定系数，并计算判别指标。

首先，由判别分析定义可知，只有当多个总体的特征具有显著的差异时，进行判别分析才有意义，且总体间差异越大，才会使误判率越小。

因此在进行判别分析时，有必要对总体多元变量的均值进行是否不等的显著性检验。

其次，利用判别分析中的费歇判别和贝叶斯判别进行判别函数的建立。

最后，利用所建立的判别函数进行回判并测得其误判率，以及对其修正。

本文利用SPSS软件实现了对总体间给类变量的均值是否不等的显著性检验并根据样本建立了相应的费歇判别函数和贝叶斯判别函数，最后进行了回判并测得了误判率，从而获得了在临床诊断中模型，给临床上的诊断试验提供了新方法和新建议。

数学建模与优化算法在医疗诊断与预测中的应用数学建模和优化算法在医疗诊断和预测中的应用已经成为了一个热门话题。

随着技术的不断发展，人们对医疗诊断和预测的需求也越来越高。

数学建模和优化算法的应用为医疗领域带来了很多好处。

本文将从数学建模和优化算法在医疗领域中的应用入手，介绍其优势和挑战。

一、数学建模在医疗诊断和预测中的应用数学建模是将现实问题抽象成数学模型，通过数学方法求解问题的过程。

在医疗领域中，数学建模可以用于疾病的诊断和预测。

例如，通过对病人的数据进行分析，可以建立一个数学模型来预测病人是否会患上某种疾病。

这种方法可以帮助医生更准确地进行诊断和治疗。

另外，数学建模还可以用于药物的研发和临床试验。

通过建立药物作用的数学模型，可以预测药物的作用机理和剂量，从而提高药物的疗效和减少副作用。

此外，数学建模还可以用于分析医院的运营效率和资源利用率，从而提高医院的管理水平。

二、优化算法在医疗诊断和预测中的应用优化算法是一种用于求解最优解的算法。

在医疗领域中，优化算法可以用于优化医疗资源的分配和病人的治疗方案。

例如，在急诊科中，优化算法可以根据患者的病情和治疗需求，合理地分配医护人员和设备资源，从而提高救治效率。

另外，优化算法还可以用于制定个性化治疗方案。

通过分析患者的基因信息、病史和生理指标等数据，可以建立一个个性化治疗模型，通过优化算法求解最佳治疗方案。

这种方法可以提高治疗效果，减少副作用，并降低医疗成本。

三、数学建模与优化算法的挑战虽然数学建模和优化算法在医疗领域中有很多应用，但是也面临着一些挑战。

首先，医学数据的质量和数量是一个问题。

医学数据通常非常复杂，需要很高的技术水平才能进行分析和处理。

其次，医学数据涉及到隐私问题，需要保护患者的隐私权。

再次，医学数据的更新速度非常快，需要及时更新数据，并且保证数据的准确性和完整性。

另外，数学建模和优化算法需要很高的技术水平和专业知识。

医生通常不具备这些技能，需要与专业人员合作才能进行应用。

数学建模疾病的诊断现要你给出疾病诊断的一种方法。

胃癌患者容易被误诊为萎缩性胃炎患者或非胃病者。

从胃癌患者中抽取5人（编号为1-5），从萎缩性胃炎患者中抽取5人（编号为6-10），以及非胃病者中抽取5人（编号为11-15），每人化验4项生化指标：血清铜蓝蛋白（X）、1蓝色反应（X）、尿吲哚乙酸（3X）、中性硫化物（4X）、测得数据如表1 2所示：表1. 从人体中化验出的生化指标根据数据，试给出鉴别胃病的方法。

论文题目：胃病的诊断摘要在临床医学中，诊断试验是一种诊断疾病的重要方法。

好的诊断试验方法将对临床诊断的正确性和疾病的治疗效果起重要影响。

因此，对于不同疾病不断发现新的诊断试验方法是医学进步的重要标志。

传统的诊断试验方法有生化检测、DNA检测和影像检测等方法。

而本文则通过利用多元统计分析中的判别分析及SPSS软件的辅助较好地解决了临床医学中胃病鉴别的问题。

在临床医学上，既提高了临床诊断的正确性，又对疾病的治疗效果起了重要效果，同时也减轻了病人的负担。

判别分析是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。

其基本原理是按照一定的判别准则，建立一个或多个判别函数，用研究对象的大量资料确定判别函数中的待定系数，并计算判别指标。

首先，由判别分析定义可知，只有当多个总体的特征具有显著的差异时，进行判别分析才有意义，且总体间差异越大，才会使误判率越小。

因此在进行判别分析时，有必要对总体多元变量的均值进行是否不等的显著性检验。

其次，利用判别分析中的费歇判别和贝叶斯判别进行判别函数的建立。

最后，利用所建立的判别函数进行回判并测得其误判率，以及对其修正。

本文利用SPSS软件实现了对总体间给类变量的均值是否不等的显著性检验并根据样本建立了相应的费歇判别函数和贝叶斯判别函数，最后进行了回判并测得了误判率，从而获得了在临床诊断中模型，给临床上的诊断试验提供了新方法和新建议。

数学建模在生物医学中的应用有哪些在当今科技飞速发展的时代，数学建模在生物医学领域的应用越来越广泛，为医学研究和临床实践带来了诸多重要的突破和创新。

数学建模，简单来说，就是用数学的语言和方法来描述和解决实际问题。

在生物医学中，它帮助我们更好地理解生命现象、疾病的发生机制，以及开发更有效的诊断和治疗方法。

数学建模在药物研发中发挥着关键作用。

药物在体内的吸收、分布、代谢和排泄过程十分复杂，通过建立数学模型，可以模拟药物在体内的动态变化。

例如，基于药代动力学和药效动力学原理建立的模型，可以预测药物在不同剂量、给药途径和时间下的浓度变化，以及药物对生理指标的影响。

这有助于优化药物的给药方案，提高治疗效果，同时减少药物的副作用。

在疾病的诊断方面，数学建模也大显身手。

以癌症为例，通过分析大量的医学影像数据、基因表达数据和临床症状等信息，建立数学模型，可以更准确地识别肿瘤的特征和发展阶段。

例如，利用机器学习算法构建的模型，可以对肿瘤的形态、大小、纹理等特征进行分析，辅助医生做出更精准的诊断。

此外，对于一些慢性疾病，如糖尿病、心血管疾病等，通过建立生理模型，可以监测生理指标的变化趋势，提前预警疾病的发生风险。

在流行病学研究中，数学建模更是不可或缺的工具。

传染病的传播是一个复杂的过程，受到人口流动、社交接触、防控措施等多种因素的影响。

建立传染病传播模型，可以模拟疾病在人群中的传播规律，预测疫情的发展趋势，为制定防控策略提供科学依据。

例如，在新冠疫情期间，基于数学模型的预测对于制定封锁措施、调配医疗资源等决策起到了重要的指导作用。

数学建模还在生物医学工程中有着广泛的应用。

比如，在人工器官的设计和优化中，通过建立流体力学模型和力学模型，可以模拟血液在人工心脏、血管中的流动情况，以及人工关节的受力情况，从而提高人工器官的性能和可靠性。

在生物材料的研发中，数学模型可以帮助预测材料在体内的降解速率、生物相容性等性能，为材料的设计和筛选提供指导。

姓名班级所在学院电话（手机）是否报名全国竞赛队长李召理学院09070241理学院队员1黄波09070241机电工程学院队员2秦建新10010642疾病诊断数学模型摘要本文解决的是如何根据就诊者体内各元素含量判别某人是否患有某种疾病和确定哪些指标是影响人们患该疾病的关键因素的问题。

通过分析可知此类问题为典型的分析判别，在此我们采用元素判别和Bayes 判别并应用Excel 和SAS 软件来对某人是否患病进行判别，并通过主成分分析法来确定患该疾病的关键因素。

对于问题一，我们采用元素判别和Bayes 判别进行前60人是否患病的判别，并对其结果进行对比。

对于元素判别，我们用Excel 对化验结果数据进行统计并通过折线图得出其分界值，然后与是否患病的真实情况进行对比，得出其准确度为95%；对于Bayes 判别，通过编写SAS 程序来进行判别，并得出其准确度为93.33%；考虑到诊断的实际情况和简便性最终确定Bayes 判别为本文所要使用的判别方法。

对于问题二，我们利用问题一中建立的判别模型对表2中的15名就诊人员的化验结果进行检验，检验结果为：9个人为患病者，6 个人为健康人员。

对于问题三，为了确定影响人们患该病的关键或主要因素，我们选取表1中的数据作为样本，建立主成分分析模型，通过对表1中的数据进行标准化并确定相关系数矩阵，接着，求出相关矩阵的特征值和特征向量，然后通过前m 个主成分的累计贡献率满足%8511≥∑∑==pk kik kλλ来确定主成分的个数，最后通过主成份载荷分析得出最能代表主成分的原指标即所要求的主要因素为Fe 、Ca 、Mg 、Cu 。

在此基础上，得到去掉K 、Na 、Zn 的化检结果的新样本，利用Bayes 判别，再对表2中的15名就诊人员的化验结果进行判别，判别结果：9个人为患病者，6 个人为健康人员。

关键词： 元素判别，Bayes 判别，主成分分析法，Excel ，SAS 软件一 问题重述.人们到医院就诊时，通常要化验一些指标来协助医生诊断。

心脏病的判别摘要本文研究的是一个判别分析类问题，解决的是如何根据就诊者的各项生理指标数据，判别就诊者是否患有心脏病以及患病的程度，并确定哪些指标是影响人们患心脏病的关键因素，从而减少化验的指标，以便人们可以及时发现疾病。

首先我们对题目中给出的数据进行了处理，通过查找资料以及合理的判断，将-9进行了合理的赋值。

问题一中，我们将250个就诊者按患病程度分为五个总体，建立了多总体fisher判别模型，利用spss软件对13个样本进行分析，剔除X L，最后得出判别函数，并根据Fisher后验概率最大这一判别规则进行回代，最终得出运用本判别方法判断“是否患病”的正确率为97.2%，判断“患病程度”的正确率为85.6%。

0问题二中，我们以问题一的判别函数和判别准则为基础，通过分析，剔除X E、X L、X，得到了新的判别函数。

然后我们运用matlab软件，将44名就诊人员13项指标的M数据代入判别函数求解，通过判断，得出各自的患病情况。

问题三中，题目要求确定影响人们患心脏病的关键或主因素，以便减少化验的指标。

为此我们运用逐步剔除法，结合spss软件，将F分布统计检定值中数值小的指标进行剔除。

当剔除F、G、B、A、D、E时，分类正确率为82.4%，而将H也剔除时，正确率降为79.6%。

因此，我们得出H、C、K、J、I、M为主要因素。

问题四中，我们运用与问题二相同的方法，将44名就诊人员13项指标的数据代入问题三得出的判别函数中进行求解，将得出的结果与问题二比较，我们发现：所建判别方法及判别准则在判断“是否患病”时，正确率较高；而在判别“患病程度”时，就有一定的偏差。

这与模型以及算法本身的准确度有一定的关系，也与我们处理数据时的正确性有一定关系。

本文最后对所建模型的优缺点进行了分析，并提出了改进与推广。

关键字：多总体fisher判别spss软件逐步剔除法心脏病的判断1．问题重述1.1问题背景心脏是维持全身血液循环的最重要器官。