合肥工业大学电磁场与电磁波孙玉发版答案
- 格式:docx
- 大小:305.53 KB
- 文档页数:8




第6章习题答案6-1 在1=r μ、4=r ε、0=σ的媒质中,有一个均匀平面波,电场强度是 若已知MHz 150=f ,波在任意点的平均功率流密度为2μw/m 265.0,试求:(1)该电磁波的波数?=k 相速?=p v 波长?=λ波阻抗?=η (2)0=t ,0=z 的电场?)0,0(=E(3)时间经过μs 1.0之后电场)0,0(E 值在什么地方?(4)时间在0=t 时刻之前μs 1.0,电场)0,0(E 值在什么地方? 解:(1))rad/m (22πεπμεω===r cfk(2)∵ 6200210265.02121-⨯===m rm av E E S εεμη∴ (V /m)1000.12-⨯=m E(3) 往右移m 15=∆=∆t v z p (4) 在O 点左边m 15处6-2 一个在自由空间传播的均匀平面波,电场强度的复振幅是 试求: (1)电磁波的传播方向?(2)电磁波的相速?=p v 波长?=λ频率?=f (3)磁场强度?=H(4)沿传播方向单位面积流过的平均功率是多少?解:(1) 电磁波沿z 方向传播。
(2)自由空间电磁波的相速m/s 1038⨯==c v p∵ πω20==ck∴ c πω20=∴ Hz 1031029⨯===c f πω(3))A/m )((10652120j )220(j 7y z x z z e e .e e E e H πππη-+--+⨯=⨯=(4))W/m (106522)Re(21211*z z av.e e H E S *-⨯=⋅=⨯=ηE E 6-3 证明在均匀线性无界无源的理想介质中,不可能存在z e E kze E j 0-=的均匀平面电磁波。
证 ∵ 0j j 0≠-=⋅∇-kzekE Ε,即不满足Maxwell 方程∴ 不可能存在z e E kze E j 0-=的均匀平面电磁波。
6-4在微波炉外面附近的自由空间某点测得泄漏电场有效值为1V/m ,试问该点的平均电磁功率密度是多少?该电磁辐射对于一个站在此处的人的健康有危险吗?(根据美国国家标准,人暴露在微波下的限制量为10-2W/m 2不超过6分钟,我国的暂行标准规定每8小时连续照射,不超过3.8×10-2W/m 2。
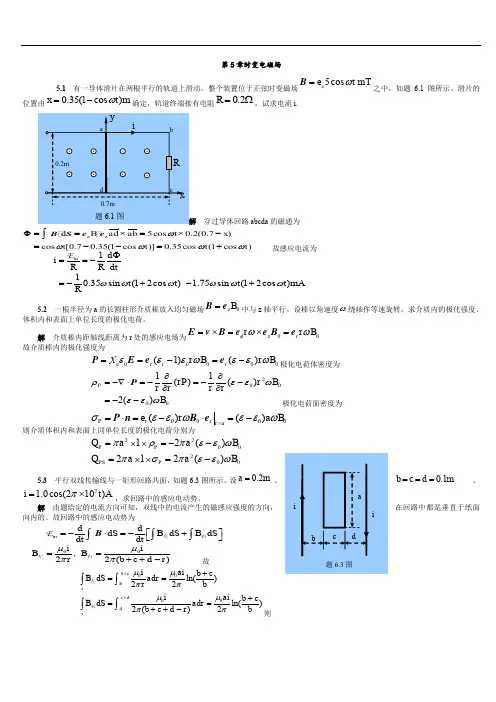
第5章时变电磁场5.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mTz e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.穿过导体回路abcda 的磁通为)cos [0.70.35(1cos )]0.35cos (1cos )z z x t t t t ωωωωΦ-=--=+ 故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E5.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X 极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P 极化电荷面密度为0000()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-5.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1mb c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
解 由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。


第6章习题答案6-1在r 1、 r 4、0的媒质中,有一个均匀平面波,电场强度是E(z,t) E m sin( t kz —)3若已知f 150 MHz ,波在任意点的平均功率流密度为0.265卩w/m 2,试求:(1) 该电磁波的波数 k ?相速V p ?波长?波阻抗 ?(2)t 0, z 0的电场 E(0,0)?(3) 时间经过0.1 之后电场E(0,0)值在什么地方?(4) 时间在t 0时刻之前0.1 口 s ,电场E(0,0)值在什么地方?—2 f —解:(1) k .——.r 2 (rad/m) cv p c/. r 1.5 108(m/s)k 1(m)(4)在O 点左边15 m 处6-2 一个在自由空间传播的均匀平面波,电场强度的复振幅是—4 j 20 z— 4 j(520 z)八、,、[/ E 10 e je x 10 ee y 伏 / 米试求:(1)电磁波的传播方向?(2) 电磁波的相速V p ?波长 ?频率f ? (3) 磁场强度H ?(4) 沿传播方向单位面积流过的平均功率是多少?=12060 (Q )(2): S a vE m0 60.265 10E m 1.00 10■. 0 r2(V/m)E(0,0)(3)往右移E m sin 8.66 103z v p t 15 m3(V/m )解:(1)电磁波沿z方向传播。
(2)自由空间电磁波的相速v p c 3 108 m/s••• k —20c20 c f —10c3 109Hz217j(20 z )z(3) H ^e z E 26510 7(e 2 e x e j20 z e y )(A/m)*(4)S av ^Re(EH *)^-^e z2.65 10 11e z (W/m 2)226-3证明在均匀线性无界无源的理想介质中,不可能存在 磁波。
证•/ EjkE °e jkz 0,即不满足Maxwell 方程不可能存在E E °e jkz e z 的均匀平面电磁波。


直角坐标系•三变量x y z •坐标表示•线元•面元•体积元dle dz e dy e dx e l d l z y x =++= ds e ds e ds e s d z z y y x x ++=zz yy xx e dxdyds e dxdz ds e dydz ds ⊥=⊥=⊥=d V d xd yd z=Az z y y x x e A e A e A e A A=++=∞dzz e d d ds e dz d ds e dz d ds ⊥=⊥=⊥=ϕρρρϕρϕρ另图见下页-5813∞dzzz e d d ds e dz d ds e dzd ds ⊥=⊥=⊥=ϕρρρϕρϕϕρρ142r ds r sin θd θd ds rsin θdrd ds rdrd θθϕϕϕ===d θϕϕ另图见下页系2r rθds r sin θd θd e ds rsin θdrd e ds rdrd θe θϕϕϕϕ=⊥=⊥=⊥-5817x y z2≤≤−∞<<∞z ϕπ2π0πθ≤≤≤≤ϕ一个专用它的大小就能完整的描示Az z e A e A=单位矢量(unit vector):A A e A=212z )A cos A cos y ==γβzz B A-5830gradient在这无穷多个方向中哪个方向的变化率三维高度场的梯度例2电位场的梯度三维高度场的梯度电位场的梯度高度场的梯度电位场的梯度与过该点的等位线垂直;数值等于该点的最大方向导数;ndSΦ= 0(无源)Φ< 0 (有负源)divergence内的通量源决定,而通量是一个积分量,仅能说明较大范围内的源分布情况,而不能说明每一点的性质。
引入散度概念。
A= ρ>0 (正源A= 0(无源)•A= −ρ<0 (负源-5850HFUT -FZG该环量表示绕线旋转趋势的大小。
水流沿平行于水管轴线方向流动Γ=0,无涡旋运动流体做涡旋运动Γ≠0,有产生涡旋的源环量矢量F 沿空间有向闭合曲线L 的线积分LF d lΓ=⋅∫环量circulation例:流速场环量密度(涡量)取不同的路径,其环量密度不同。

习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ,如果把它移动到无穷远处,需要作多少功?解:用镜像法计算。
导体面上的感应电荷的影响用镜像电荷来代替,镜像电荷的大小为-Q ,位于和原电荷对称的位置。
当电荷Q 离导体板的距离为x 时,电荷Q 受到的静电力为2)2(042x Q F επ-=静电力为引力,要将其移动到无穷远处,必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中,外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以,在整个过程中,外力作的总功为dq8/2επ。
也可以用静电能计算。
在移动以前,系统的静电能等于两个点电荷之间的相互作用能:d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+= 移动点电荷Q 到无穷远处以后,系统的静电能为零。
因此,在这个过程中,外力作功等于系统静电能的增量,即外力作功为dq8/2επ。
5.2 一个点电荷放在直角导体内部(如图5-1),求出所有镜像电荷的位置和大小。
解:需要加三个镜像电荷代替 导体面上的感应电荷。
在(-a ,d )处,镜像电荷为-q ,在(错误!链接无效。
镜像电荷为q ,在(a ,-d )处,镜像电荷为-q 。
5.3 证明:一个点电荷q 和一个带有电 荷Q 、半径为R 的导体球之间的作用力为]2)22(2[04R D DRq D D qR Q q F --+=επ其中D 是q 到球心的距离(D >R )。
证明:使用镜像法分析。
由于导体球不接地,本身又带电Q ,必须在导体球内加上两个镜像电荷来等效导体球对球外的影响。
在距离球心b=R 2/D 处,镜像电荷为q '= -Rq/D ;在球心处,镜像电荷为D Rq Q q Q q /2+='-=。

第二章 静电场重点和难点电场强度及电场线等概念容易接受,重点讲解如何由物理学中积分形式的静电场方程导出微分形式的静电场方程,即散度方程和旋度方程,并强调微分形式的场方程描述的是静电场的微分特性或称为点特性。
利用亥姆霍兹定理,直接导出真空中电场强度与电荷之间的关系。
通过书中列举的4个例子,总结归纳出根据电荷分布计算电场强度的三种方法。
至于媒质的介电特性,应着重说明均匀和非均匀、线性与非线性、各向同性与各向异性等概念。
讲解介质中静电场方程时,应强调电通密度仅与自由电荷有关。
介绍边界条件时,应说明仅可依据积分形式的静电场方程,由于边界上场量不连续,因而微分形式的场方程不成立。
关于静电场的能量与力,应总结出计算能量的三种方法,指出电场能量不符合迭加原理。
介绍利用虚位移的概念计算电场力,常电荷系统和常电位系统,以及广义力和广义坐标等概念。
至于电容和部分电容一节可以从简。
重要公式真空中静电场方程:积分形式:⎰=⋅SS E 0d εq⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E已知电荷分布求解电场强度:1,)()(r r E ϕ-∇=; ⎰''-'=V Vd )(41)(|r r |r r ρπεϕ2,⎰'''-'-'=V V 3d |4))(()(|r r r r r r E περ3,⎰=⋅SS E 0d εq高斯定律介质中静电场方程:积分形式:q S=⋅⎰ d S D⎰=⋅ll E 0d微分形式:ρ=⋅∇D0=⨯∇E线性均匀各向同性介质中静电场方程:积分形式:εqS=⋅⎰ d S E⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E静电场边界条件:1,t t E E 21=。
对于两种各向同性的线性介质,则2211εεttD D =2,s n n D D ρ=-12。
在两种介质形成的边界上,则n n D D 21=对于两种各向同性的线性介质,则n n E E 2211εε=3,介质与导体的边界条件:0=⨯E e n ; S n D e ρ=⋅若导体周围是各向同性的线性介质,则ερS n E =;ερϕS n -=∂∂静电场的能量:孤立带电体的能量:Q C Q W e 21212Φ== 离散带电体的能量:∑==ni i i e Q W 121Φ分布电荷的能量:l S V W l l S S Ve d 21d 21d 21ρϕρϕρϕ⎰⎰⎰===静电场的能量密度:E D ⋅=21e w 对于各向同性的线性介质,则2 21E w e ε=电场力:库仑定律:rrq q e F 2 4πε'=常电荷系统:常数=-=q e lW F d d常电位系统:常数==ϕlW F e d d题 解2-1 若真空中相距为d 的两个电荷q 1及q 2的电量分别为q 及4q ,当点电荷q '位于q 1及q 2的连线上时,系统处于平衡状态,试求q '的大小及位置。
合肥工业大学电磁场与电磁波(孙玉发版)第4章答案本页仅作为文档封面,使用时可以删除This document is for reference only-rar21 year.Marchx两边同乘以sin(—),并从o 到“对y 积分,得到by . nny2U {} \ 1 1 ・严兀八」 2U° b .川兀d 、A"二〒片产n (〒心+〒比-尹皿〒)2崙严(〒)故得到 必r,y)=组$ +警£,sin (型)sin (空)e 「曲 b d7T 畚,厂 bh如题图所示的导体槽.底面保持电位〃0,其余两浙电位为零,求槽内的电位的解。
解很据题意.电位(p(x. y)满足的边界条件为第四章习題解答★【】如题图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零.上边盖扳的电位为 “0,求槽内的电位函数。
解根据题慰.电位0(x,y)满足的边界条件为①0(0,刃=(p{a. y)=0:②^(A \0) = 0:③<p(x,b) = U Q 根据条件①和②,电位(p{x. y)的通解应取为000(x ,y) =〉2>ksinh(^))sin(^?)由条件③,有 Zi a "U Q = £ A,sinh( —) sin (匕丄) -I a annx , zc/n r ・ mx 、,两边同乘以sin(——),并从o 到a 对x 积分,得到厲= 一 sin(——)dx =a tzsinh( n7rb : a) J a 4/ 2U° (1 — COS ,?JT )= 7?-Tsinh( n7rb/a)・,/ , z 」1 = 1,3,5,•… /i>rsinn( n7rb/a)0 t 刃=2,4,6,•…z、 4〃()匸 1 ・ | nny ・ nnx故得到槽内的电位分布0(圮刃=—- Y ——— sinh(——)sin(——)7t ... n sinh (7?7r/?/6/) a a两平行无限大导体平面.距离为其间有一极薄的导体片由y = d 到y = b(—svxvs)。
第四章习题解答★【4.1】如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为①(0,)(,)0y a y ϕϕ==;② (,0)0x ϕ=; ③ 0(,)x b U ϕ= 根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a aππϕ∞==∑ 由条件③,有两边同乘以sin()n xa π,并从0到a 对x 积分,得到002sin()d sinh()an U n x A x a n b a a ππ==⎰ 故得到槽内的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑L 4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:22(,0)(,)0x x b ϕϕ==① 2(,)0()x y x ϕ=→∞② ③002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩; 根据条件①和②,可设2(,)x y ϕ的通解为21(,)sin()en x bn n n yx y A b ππϕ∞-==∑;由条件③有 00100(0)sin()()n n U U y y d n y b A U U b y yd y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n ybπ,并从0到b 对y 积分,得到 故得到 (,)x y ϕ=0022121sin()sin()e n x b n U bU n d n y y b d n b bππππ∞-=+∑ 4.4 如题4.4图所示的导体槽,底面保持电位0U ,其余两面电位为零,求槽内的电位的解。
《电磁场与电磁波》知识点及参考答案第1章矢量分析1、如果矢量场F的散度处处为o,即' F = 0,则矢量场是无散场,由旋涡源所产生,通过任何闭合曲面S的通量等于0。
2、如果矢量场F的旋度处处为o,即' F = 0,则矢量场是无旋场,由散度源所产生,沿任何闭合路径C的环流等于0。
3、矢量分析中的两个重要定理分别是散度定理(高斯定理)和斯托克斯定理,它们的表达式分别是:散度(高斯)定理:V Fdv八s F dS和斯托克斯定理:• s' F dS八:c F d。
4、在有限空间V中,矢量场的性质由其散度、旋度和V边界上所满足的条件唯一的确定。
(V)5、描绘物理状态空间分布的标量函数和矢量函数,在时间为一定值的情况下,它们是唯一的。
(V )6、标量场的梯度运算和矢量场的旋度运算都是矢量。
(V )7、梯度的方向是等值面的切线方向。
(X )8、标量场梯度的旋度恒等于0。
(V )9、习题 1.12, 1.16。
第2章电磁场的基本规律(电场部分)1静止电荷所产生的电场,称之为静电场;电场强度的方向与正电荷在电场中受力的方向相同。
2、在国际单位制中,电场强度的单位是V/m(伏特/米)。
■ ■3、静电系统在真空中的基本方程的积分形式是:' s D・dS=.v匚dV二(和■ —■\i E dl =0。
4、静电系统在真空中的基本方程的微分形式是:'、• D =『V和E = 0。
5、电荷之间的相互作用力是通过电场发生的,电流与电流之间的相互作用力是通过磁场发生的。
T T6、在两种媒质分界面的两侧,电场E的切向分量E it —E2t = 0;而磁场B的法向分量B in—B 2n = 0。
1 2 1 27、在介电常数为e的均匀各向同性介质中,电位函数为二一X - y -5z,则电场强度2 2E = - xe x - ye y 5e z 。
&静电平衡状态下,导体内部电场强度、磁场强度等于零,导体表面为等位面;在导体表面只有电场的法向分量。
第四章习题解答★【】如题图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ==;② (,0)0x ϕ=; ③ 0(,)x b U ϕ= 根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a a ππϕ∞==∑ 由条件③,有 01sinh()sin()n n n b n xU A a a ππ∞==∑两边同乘以sin()n xa π,并从0到a 对x 积分,得到002sin()d sinh()an U n x A x a n b a a ππ==⎰ 02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩,故得到槽内的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n x x y n n b a a aππϕππ==∑ 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:22(,0)(,)0x x b ϕϕ==① 2(,)0()x y x ϕ=→∞②③ 002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩; 根据条件①和②,可设2(,)x y ϕ的通解为21(,)sin()en x bn n n yx y A b ππϕ∞-==∑;由条件③有 00100(0)sin()()n n U U y y d n y b A U U b y yd y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n ybπ,并从0到b 对y 积分,得到 0002211(1)sin()d ()sin()d d bn dU U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d b ππ 故得到 (,)x y ϕ=0022121sin()sin()e n x b n U bU n d n y y b d n b bππππ∞-=+∑ 如题图所示的导体槽,底面保持电位0U ,其余两面电位为零,求槽内的电位的解。
解 根据题意,电位(,)x y ϕ满足的边界条件为a题图题 图(0,)(,)0y a y ϕϕ== ① (,)0()x y y ϕ→→∞ ② 0(,0)x U ϕ=③②,电位(,)x y ϕ的通解应取为根据条件①和1(,)sin()n n n y an x x y A ea ππϕ∞-==∑;由条件③,有 01sin()n n n x U A a π∞==∑sin()n xaπ,并从0到a 对x 积分,得到002sin()d an U n x A x a a π==⎰ 两边同乘以02(1cos )U n n ππ-=04,1,3,5,02,4,6,U n n n π⎧=⎪⎨⎪=⎩,;故得到01,3,5,41(,)sin()n y a n U n xx y e n aππϕπ-==∑★【】一长、宽、高分别为a 、b 、c 的长方体表面保持零电位,体积内填充密度为()sin()sin()x zy y b a cππρ=- 的电荷。
求体积内的电位ϕ。
解 在体积内,电位ϕ满足泊松方程22222201()sin()sin()x zy y b x y z a cϕϕϕππε∂∂∂++=--∂∂∂ (1) 长方体表面S 上,电位ϕ满足边界条件0S ϕ=。
由此设电位ϕ的通解为11101(,,)sin()sin()sin()mnp m n p m x n y p zx y z A a b cπππϕε∞∞∞====∑∑∑,代入泊松方程(1),可得 222111[()()()]mnp m n p m n p A a b cπππ∞∞∞===++⨯∑∑∑ sin()sin()sin()m x n y p z a b c πππ=()sin()sin()x z y y b a cππ-由此可得 0mnpA = (1m ≠或1)p ≠ ;222111[()()()]sin()n p n n yA a b c b ππππ∞=++=∑()y y b - (2)由式(2),得 2221102[()()()]()sin()d bn n n y A y y b y a b c b b ππππ++=-=⎰34()(cos 1)b n b n ππ-= 2381,3,5,()02,4,6,b n n n π⎧-=⎪⎨⎪=⎩; 故2532221,3,5,81(,,)sin()sin()sin()11[()()()]n b x n y zx y z n a b c n a b cπππϕπε∞==-++∑★【】如题图所示的一对无限大接地平行导体板,板间有一与z 轴平行的线电荷l q ,其位置为),0(d 。
求板间的电位函数。
解 由于在(0,)d 处有一与z 轴平行的线电荷l q ,以0x=为界将场空间分割为0x >和0x <两个区域,则这两个区域中的电位1(,)x y ϕ和2(,)x y ϕ都满足拉普拉斯方程。
而在0x =的分界面上,可利用δ函数将线电荷l q 表示成电荷面密度0()()l y q y y σδ=-。
电位的边界条件为11(,0)(,)0x x a ϕϕ== ,22(,0)(,)0x x a ϕϕ== ①1(,)0x y ϕ→()x →∞,2(,)0x y ϕ→()x →-∞② 12(0,)(0,)y y ϕϕ= , 21()()lx q y d x xϕϕδε=∂∂-=--∂∂③题 图题图a由条件①和②,可设电位函数的通解为11(,)sin()n n n x an y x y A ea ππϕ∞=-=∑ (0)x >21(,)sin()n n n x a n y x y B e a ππϕ∞==∑ (0)x <由条件③,有1sin()n n n y A a π∞==∑1sin()nn n y B a π∞=∑ (1) 1sin()n n n n y A a a ππ∞=--∑1sin()n n n n yB a a ππ∞=∑ 0()l q y d δε=- (2)由式(1),可得 n n A B = (3);将式(2)两边同乘以sin()m yaπ,并从0到a 对y 积分,有n n A B +002()sin()d a l q n yy d y n aπδπε=-=⎰02sin()l q n d n a ππε (4) 由式(3)和(4)解得sin()l n n q n dA B n aππε==故 1101(,)sin()sin()ln n x a q n d n y x y e n a a πππϕπε∞=-=∑ (0)x > 2101(,)sin()sin()l n n x q n d n yx y e n a aπππϕπε∞==∑ (0)x < 如题图所示的矩形导体槽的电位为零,槽中有一与槽平行的线电荷l q 。
求槽内的电位函数。
解 由于在),(00y x 处有一与z 轴平行的线电荷l q ,以0x x =为界将场空间分割为00x x <<和0x x a <<两个区域,则这两个区域中的电位1(,)x y ϕ和2(,)x y ϕ都满足拉普拉斯方程。
而在0x x =的分界面上,可利用δ函数将线电荷l q 表示成电荷面密度0()()l y q y y σδ=-,电位的边界条件为① 1(0,)0y =ϕ,2(,)0a y ϕ=,② 11(,0)(,)0x x b =ϕϕ=,22(,0)(,)0x x b =ϕϕ=③ 1020(,)(,)x y x y ϕϕ=02100()()lx x q y y x xϕϕδε=∂∂-=--∂∂由条件①和②,可设电位函数的通解为11(,)sin()sinh()n n n y n xx y A b b ππϕ∞==∑ )0(0x x << 2(,)x y ϕ=1sin()sinh[()]n n n y n B a x b b ππ∞=-∑ )(0a x x << 由条件③,有0011sin()sinh()sin()sinh[()]n nn n n x n y n y n A B a x b b b b ππππ∞∞===-∑∑ (1) 01sin()cosh()n n n x n n y A b b b πππ∞=-∑01sin()cosh[()]n n n n y n B a x b b b πππ∞=-∑)(00y y q l -δε= (2) 由式(1),可得00sinh()sinh[()]0n n n x n A B a x b b ππ--= (3)将式(2)两边同乘以sin()m ybπ,并从0到b 对y 积分,有)](cosh[)cosh(00x a bn B b x n A n n -π+π0002()sin()d b l q n y y y y n b πδπε=-=⎰002sin()l q n y n b ππε (4)题图由式(3)和(4)解得00021sinh[()]sin()sinh()l n q n y n A a x n a n b bππππε=-00021sinh()sin()sinh()l n q n x n y B n a b n b b ππππε=故 101021(,)sinh[()]sinh()ln q n x y a x n n a b b πϕπεπ∞==-∑0sin()sinh()sin()n y n x n yb b b πππ⋅,)0(0x x << 021021(,)sinh()sinh()l n q n x x y n n a b b πϕπεπ∞==∑0sin()sinh[()]sin()n y n n ya xb b b πππ⋅-,)(0a x x << 若以0y y =为界将场空间分割为00y y <<和0y y b <<两个区域,则可类似地得到101021(,)sinh[()]sinh()ln q n x y b y n n b a a πϕπεπ∞==-∑0sin()sinh()sin()n x n y n xa a a πππ⋅ 0(0)y y << 021021(,)sinh()sinh()l n q n y x y n nb a a πϕπεπ∞==∑0sin()sinh[()]sin()n x n n xb y a a aπππ⋅- 0()y y b << * 如题图所示,在均匀电场00x E E e =中垂直于电场方向放置一根无限长导体圆柱,圆柱的半径为a 。