THUSSAT2019年9月诊断性测试文科数学试卷
- 格式:pdf
- 大小:404.20 KB
- 文档页数:2

四川高三联合诊断考试数学试题(文科)参考答案及评分意见一㊁选择题:1.A㊀2.D㊀3.C㊀4.A㊀5.B㊀6.D㊀7.C㊀8.C㊀9.B㊀10.D㊀11.C㊀12.A二㊁填空题:13.-2㊀㊀㊀14.5㊀㊀㊀㊀15.8㊀㊀㊀㊀16.(12,916)三㊁解答题:17.解:(1)由直方图,可得(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)ˑ0.5=1,解得a=0.30. 5分(2)因为前6组频率之和为(0.08+0.16+0.30+0.40+0.52+0.30)ˑ0.5=0.88>0.85. 7分而前5组的频率之和为(0.08+0.16+0.30+0.40+0.52)ˑ0.5=0.73<0.85.所以2.5ɤx<3. 9分由0.3ˑ(x-2.5)=0.85-0.73解得x=2.9.因此,估计月用水量标准为2.9吨,85%的居民每月的用水量不超过标准.12分18.解:(1)因为sin(A+C)cos B=3cos2B-32,所以2sin(A+C)cos B=3(2cos2B-1),又A+B+C=π,所以sin2B=3cos2B,即tan2B=3, 3分因为B为锐角,所以2Bɪ(0,π),所以2B=π3,所以B=π6. 6分(2)由(1)知B=π6,由余弦定理得cos B=a2+c2-b22ac,即a2+c2-3ac-1=0 8分因为a2+c2ȡ2ac㊀所以acɤ2+3(当且仅当a=c=6+22时取等号). 10分所以SәABC=12ac sin Bɤ2+34(当且仅当a=c=6+22时取等号),故әABC的面积的最大值是2+34. 12分19.(1)证明:因为长方形ABCD 中,AB =22,AD =2,M 为DC 的中点,所以AM =BM =2,所以BM ʅAM ,因为平面ADM ʅ平面ABCM ,平面ADM ɘ平面ABCM =AM ,BM ⊂平面ABCM ,所以BM ʅ平面ADM ,因为AD ⊂平面ADM ,所以AD ʅBM. 6分(2)解:过D 作DG ʅAM 于G ,连BG ,取BG 中点O ,连结EO ,因为平面ADM ʅ平面ABCM ,平面ADM ɘ平面ABCM =AM ,所以DG ʅ平面ABCM ,8分因为E 为DB 的中点,所以EO ʏ12DG ,所以EO ʅ平面ABM ,由已知可得,S әABM =12AM ㊃BM =12ˑ2ˑ2=2,S 梯形ABCM =(AB +MC )ˑAD 2=32ˑ22=3. 10分所以三棱锥E -ABM 与四棱锥D -ABCM 的体积的比值为12ˑ23=13. 12分20.解:(1)当a =1时,f (x )=x 22-ln x ,则f ᶄ(x )=x -1x ,所以f ᶄ(1)=0,又f (1)=12. 2分所以曲线y =f (x )在(1,f (1))处的切线方程为y -12=0ˑ(x -1),即y =12. 5分(2)由f (x )=x 22-a ln x 得f ᶄ(x )=x -a x =x 2-a x (x >0).①当a ɤ0时,f ᶄ(x )>0,函数f (x )在(0,+ɕ)上单调递增,函数无极大值,也无极小值; 7分②当a >0时,由f ᶄ(x )=0得x =a 或-a (舍负),于是当0<x <a 时,f ᶄ(x )<0,f (x )在(0,a )上单调递减;当x >a 时,f ᶄ(x )>0,f (x )在(a ,+ɕ)上单调递增,函数f (x )在x =a 处取得极小值f (a )=a (1-ln a )2,无极大值. 10分综上所述:当a ɤ0时,函数f (x )的单调递增区间为(0,+ɕ),函数f (x )既无极大值也无极小值;当a >0时,函数f (x )的单调递减区间是(0,a ),单调递增区间是(a ,+ɕ),函数f (x )有极小值a (1-ln a )2,无极大值. 12分21.解:(1)证明:由题意设l 的方程为y =kx +4,联立y =kx +4,x 2=8y ,{得x 2-8kx -32=0㊀因为ә=(-8k )2-4ˑ(-32)>0,所以设A (x 1,y 1),B (x 2,y 2),则x 1x 2=-32. 3分设直线PA ,PB 的斜率分别为k 1,k 2,对y =x 28求导得yᶄ=x 4,所以k 1=x 14,k 2=x 24,所以k 1k 2=x 14㊃x 24=x 1x 24ˑ4=-3216=-2(定值). 6分(2)解:由(1)可得直线PA 的方程为㊀㊀y -x 218=x 14(x -x 1)㊀①直线PB 的方程为㊀㊀y -x 228=x 24(x -x 2)㊀②联立①②,得点P 的坐标为(x 1+x 22,x 1x 28), 8分由(1)得x 1+x 2=8k ,x 1x 2=-32,所以P (4k ,-4).于是|AB |=81+k 2k 2+2,点P 到直线AB 的距离d =4(k 2+2)1+k 2, 10分所以S әPAB =16k 2+2(k 2+2),当k 2=0,即k =0时,әPAB 的面积取得最小值322. 12分22.解:(1)设圆上任意一点坐标为(ρ,θ),由余弦定理得:(3)2=ρ2+(2)2-2ρˑ2ˑcos(θ-π4)整理得:ρ2-2ρ(cos θ+sin θ)-1=0(经检验,当圆心极点与圆上的点三点在一直线上时也适合).所以圆C 的极坐标方程为ρ2-2ρ(cos θ+sin θ)-1=0. 5分(2)因为x =ρcos θ,y =ρsin θ.所以圆的直角坐标方程为x 2+y 2-2x -2y -1=0,将直线l 的参数方程代入圆的直角坐标方程得:(2+t cos α)2+(2+t sin α)2-2(2+t cos α)-2(2+t sin α)-1=0,整理得:t 2+(2cos α+2sin α)t -1=0,设t 1,t 2为该方程的两根,所以t 1+t 2=-2cos α-2sin α,t 1t 2=-1,所以|AB |=|t 1-t 2|=(t 1+t 2)2-4t 1t 2=8+4sin2α,因为αɪ[0,π4),所以2αɪ[0,π2)所以|AB |ɪ[22,23). 10分23.解:(1)|2x -1|>|x +2|,即4x 2-4x +1>x 2+4x +43x 2-8x -3>0,解得x <-13或x >3,所以f (x )>0的解集为{x |x <-13或x >3}.5分(2)f (x )=|2x -1|-|x +2|=-x +3,x <-2,-3x -1,-2ɤx <12,x -3,x ȡ12,ìîí故f (x )的最小值为f (12)=-52.因为存在x 0ɪR ,使得f (x 0)+2m 2<4m,所以4m -2m 2>-52,解得-12<m <52,故m 的取值范围是(-12,52).10分。

2019年高三数学文科9月第二次阶段考试题(有答案)2019年高三数学文科9月第二次阶段考试题(有答案)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的1.函数的定义域为( )A. (0,1)B. [0,1)C. (0,1]D.[0,1]2. 函数f(x)=xa的图象过点,则f[f(9)]=( )A. B.3 C. D.3.若f(x)是偶函数,且当x[0,+)时,f(x)=x-1,则f(x-1)0的解集是A.(-1,0)B.(-,0)(1,2)C. (1,2)D.(0,2)4.已知曲线与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )A.- 2B.2C.D.15.下列函数图像中,正确的是( )6.若定义在R上的函数f(x)满足:对任意x1,x2R有f(x1+x2)=f(x1)+f(x2)+1,则下列说法一定正确的是( )A.f(x)-1是奇函数B. f(x)-1是偶函数C. f(x)+1是奇函数D.f(x)+1是偶函数11.偶函数f(x)满足f (x-1)=f (x+1),且当x[0,1]时,f (x)=-x+1,则关于x的方程f (x)=lg(x+1)在x[0,9]上解的个数是( )A.7B.8C.9D.1012. 定义在R上的函数f(x),当x(-1,1]时,f (x)=x2-x,且对任意的x满足f (x-2)=af (x)(常数a0),则函数f(x)在区间(5,7]上的最小值是( )A. B. C. D.二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13.函数的定义域为.14. 若函数y=x2+(a+2)x+3(x[a,b])的图象关于直线x=1对称,则b=___________.15.函数在R上是减函数,则实数a的取值范围是___________.16.已知函数f(x) =x3+mx2+(m+6)x+1既存在极大值又存在极小值,则实数m的取值范围是____.三、解答题(本大题6小题,共70分。


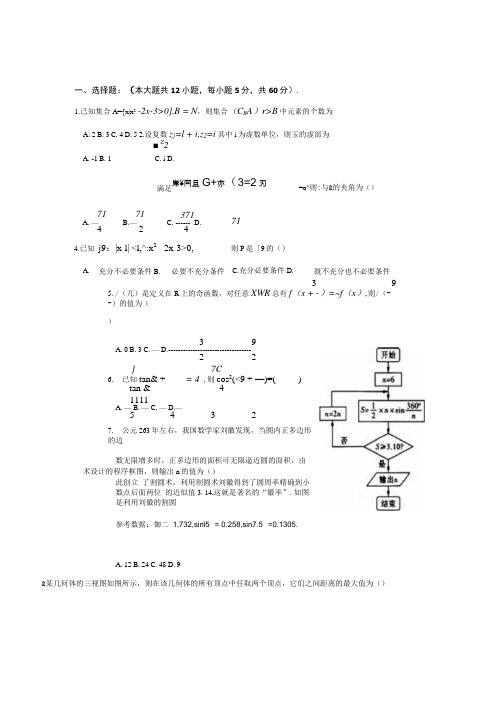
一、选择题:(本大题共12小题,每小题5分,共60分).1.己知集合A={x|x 2 -2x-3>0],B = N ,则集合(C R A )r>B 中元素的个数为A. 2B. 3C. 4D. 5 2.设复数z }=l + i,z 2=i 其中i 为虚数单位,则玉的虚部为■ Z 23 95. /(兀)是定义在R 上的奇函数,对任意XWR 总有f (x + -)=~f (x ),则/(--)的值为()3 9 A. 0 B. 3 C. — D. ---------------------------------- 2 2]7C 6.已知tan& + ------ = 4 ,则cos 2(<9 + —)=( ) tan & 4 1111 A. — B. — C. — D.— 5 4 3 2 7. 公元263年左右,我国数学家刘徽发现,当圆内正多边形的边数无限增多时,正多边形的面积可无限逼近圆的面积,由此创立 了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位 的近似值3. 14,这就是著名的“徽率”.如图是利用刘徽的割圆参考数据:御二 1,732,sinl5° = 0.258,sin7.5° =0.1305.A. 12B. 24C. 48D. 9&某几何体的三视图如图所示,则在该几何体的所有顶点中任取两个顶点,它们之间距离的最大值为() A. -1 B. 1 C. i D.满足 岸¥冃且G+亦(3=2刃 =o^则:与&的夹角为()71 71 A. — B.— 4 2 4.已知 j9:|x-l| <l,^:x 2 - 2x-3>0, 371 C. ------ D. 4 71则P 是「9的()A. 充分不必要条件B. 必要不充分条件C.充分必要条件D.既不充分也不必要条件 术设计的程序框图,则输出n 的值为()9. 设有下面四个命题:① “若a>0,则:与忌与的夹角为锐角”及它的逆命题均为真命题② 若 R,2X > 0,则—\p : 3x 0 e R,2X ° < 0③ “ ab<l ”是“ Q W1或b<l ff 的充分不必要条件④ 命题“ AABC 中,若A>B ,则sin A > sin B "的逆命题为真命题其中正确命题的个数是()A. 3B. 2C. 1D. 010. 已知定义在7?上的函数/(x-1)的图像关于兀=1对称,且当兀〉0时,/(兀)单调递减,若 a = f(logQ 5 3),Z? = /(0.5-13),c = /(0.76)则 a.b.c 的大小关系是()二、填空题:(本大题共4小题,每小题5分,共20分).14.在正方体ABCD-A.B.C.D.中,对角线AC ;与底面ABCD 所成角的正弦值为.侧视图A . c> a> bB . b> a> c c. a> c>b D . c>b> a 又AD DC = 0,则BD 的最大值为( D . 2A /212.己知函数y (x ) = -- — ax' XX e (0,+8),当%2 >%!时,不等式丿凶 无2 也。

中学生标准学术能力诊断性测试2023年9月测试数学试卷本试卷共150分,考试时间120分钟。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{}11,,1522x A x x B x x x −⎧⎫=<∈=∈<<⎨⎬+⎩⎭R N ,则A B =A .{}2B .{}2,3 C .{}3,4 D .{}2,3,42.欧拉公式i e cos isin θθθ=+把自然对数的底数e 、虚数单位i 、三角函数联系在一起,充分体现了数学的和谐美.已知实数指数幂的运算性质同样也适用于复数指数幂,则i i =A .2e πB .2eπ−C .eπD .e−π3.已知等比数列{}n a 的前n 项和为n S ,若124816S S S =+,则公比q = A .3B .2±C .2D .3±4.已知向量6AB AC ⋅=,线段BC 的中点为M ,且6AM =,则BC =A.B.C.D.5.已知函数()()sin 03f x x ωωπ⎛⎫=+> ⎪⎝⎭的周期为T ,且满足2T >π,若函数()f x 在区间,64ππ⎛⎫⎪⎝⎭不单调,则ω的取值范围是 A .,143⎛⎫ ⎪⎝⎭B .1,12⎛⎫ ⎪⎝⎭C .2,13⎛⎫⎪⎝⎭D .4,15⎛⎫⎪⎝⎭6.三棱锥A BCD −中,3,,43AB BC BD ABC ABD DBC ππ===∠=∠=∠=,则直线AD与平面ABC 所成角的正弦值是 A.17B.29C.17D.297.已知三角形ABC 中,3BC =,角A 的平分线交BC 于点D ,若12BD DC =,则三角形ABC 面积的最大值为 A .1 B .2C .3D .48.比较0.111101,ln1.2,10115ea b c =−==的大小 A .a c b >>B .b c a >>C .b a c >>D .a b c >>二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对但不全得3分,有错选的得0分. 9.已知实数a b c ,,满足a b c >>,且1abc =,则下列说法正确的是A .()21a c b+>C .22a b >B .11a cb c<−−D .()()22110a b ab −−>10.已知10个样本数据,若去掉其中最大和最小的数据,设剩下的8个样本数据的方差为21s ,平均数1x ;最大和最小两个数据的方差为22s ,平均数2x ;原样本数据的方差为2S ,平均数x ,若12x x =,则A .剩下的8个样本数据与原样本数据的中位数不变B .1x x =C .剩下8个数据的下四分位数大于与原样本数据的下四分位数D .222124155S s s =+11.已知函数()cos22sin f x x x =+,则A .函数()f x 在区间,62ππ⎛⎫⎪⎝⎭上单调递增 B .直线2x π=是函数()f x 图象的一条对称轴 C .函数()f x 的值域为31,2⎡⎤⎢⎥⎣⎦D .方程()()()0,2f x a x =∈π最多有8个根,且这些根之和为8π12.已知椭圆22:12x C y +=的中心为O ,,A B 是C 上的两个不同的点且满足OA OB ⊥,则A .点O 在直线AB 上投影的轨迹为圆B .AOB ∠的平分线交AB 于D 点,OD的最小值为3C .AOB ∆面积的最小值为23D .AOB ∆中,AB边上中线长的最小值为3三、填空题:本题共4小题,每小题5分,共20分. 13.已知tan 2α=,则sin 4α= . 14.若()52210012103x x a a x a x a x −−=++++,则12345a a a a a ++++= .15.已知四棱锥的各个顶点都在同一个球面上.若该球的体积为36π,则该四棱锥体积的最大值是 .16.已知函数()()21e sin 112xf x m x x m x =+−−++,在0x =处取到极小值,则实数m = .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知{}n a 是各项均为正数的等比数列,设3log n n c a =,若数列{}n c 的前n 项和22n n nS +=. (1)求数列{}n a 的通项公式;(2)记()2265n n d a n n =⋅++,求数列{}n d 的前n 项和n T .18.(12分)记ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2cos cos cos2c a A B b A=−()A B ≤.(1)求A ;(2)若D 是BC 上的一点,且:1:2,2BD DC AD ==,求a 的最小值.19.(12分)某单位组织知识竞赛,有甲、乙两类问题.现有A ,B ,C 三位员工参加比赛,比赛规则为:先从甲类问题中随机抽取一个问题回答,若回答错误则该员工比赛结束;若回答正确再从乙类问题中随机抽取一个问题回答,无论回答正确与否,该员工比赛结束.每人两次回答问题的过程相互独立.三人回答问题也相互独立.甲类问题中每个问题回答正确得20分,否则得0分;乙类问题中每个问题回答正确得80分,否则得0分.已知A 员工能正确回答甲类问题的概率为0.5,能正确回答乙类问题的概率为0.6;B 员工能正确回答甲类问题的概率为0.6,能正确回答乙类问题的概率为0.5;C 员工能正确回答甲类问题的概率为0.4,能正确回答乙类问题的概率为0.75.(1)求3人得分之和为20分的概率;(2)设随机变量X 为3人中得分为100的人数,求随机变量X 的数学期望. 20.(12分)已知四棱锥S ABCD −中,底面ABCD是矩形,,2SA BD SA AD ⊥==,M 是SB 的中点.(1)证明:MC BD ⊥;(2)若,2SA AD SA ⊥=,点P 是SC 上的动点,直线AP 与平面AMC,求SP SC. 21.(12分)已知椭圆()222:106x y C b b+=>的左右焦点分别为12,F F ,C 是椭圆的中心,点M 为其上的一点满足125,2MF MF MC ⋅==.(1)求椭圆C 的方程;(2)设定点(),0T t ,过点T 的直线l 交椭圆C 于,P Q 两点,若在C 上存在一点A ,使得直线AP的斜率与直线AQ 的斜率之和为定值,求t 的范围.22.(12分)已知函数()()ln e ee 0axxf x a x x =−−>. (1)当1a =时,求函数()()1e eax f x g x x a −=−+−的单调区间;(2)证明:当2e a −<−时,不等式()0f x >恒成立.(第20题图)中学生标准学术能力诊断性测试2023年9月测试数学参考答案一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对但不全的得3分,有错选的得0分.三、填空题:本题共4小题,每小题5分,共20分.13.2425−14.46−15.64316.1四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)(1)()22111,22n n n n n n S S −−+−+=∴=, ()11,n n n S S n c n n −∴−==>∈N ·································································· 2分又()111,,3nn n c S c n n a ==∴=∈∴=N + ······················································· 3分(2)()()()2212326511313n n n n d n n n n +⎡⎤=⨯++=++⨯−+⨯⎣⎦····························· 7分()()()()2222322213113313213n T =+⨯−+⨯++⨯−+⨯++∴()()()()2221121311311313n n n nnn n n −+⎡⎤⎡⎤+⨯−−+⨯+++⨯−+⨯⎣⎦⎣⎦()()221113113n n +⎡⎤=−+⨯+++⨯⎣⎦212236 101812 12sin 2sin cos cos sin cos 2C A A B B A ∴=−···················································· 2分 ()sin sin 2cos sin cos2sin 20C A B B A A B ∴=−=−> ··································· 4分又02A B <−<π,则2C A B =−或2C A B +−=π,若2C A B =−,则3A π=; 若2C A B +−=π,则2A B =,又A B ≤,不符合题意,舍去,综上所述3A π= ························································································· 6分 (2)()22222,,33AB ACAB AC BD DC AD AD ⎛⎫++=∴=∴= ⎪⎝⎭···························· 8分 224236b c bc ∴++= ①,又222a b c bc =+− ②,①÷②得:222222242131426c c b b a b c bc c c b c b bc b ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==+−⎛⎫⎛⎫−+ ⎪ ⎪⎝⎭⎭+⎝········································ 9分 令cx b=,又22222,,,A B a b a b b c bc b ≤≤≤∴+−≤∴∴, ,01cc b x b∴≤∴<=≤, 令()()()222142111,6430f x x f x x x x x x x x +=<≤=+−+−+−+······························ 10分令363,6t x t x +−==, ()()()()23636433,4332727t f t t f t t t t t∴=+−<≤∴=+−<≤++,又2712t t +≥或()2273612,17,7,7t f t a t a +<−∴<≤∴≤∴≥, 所以当三角形ABC 为等边三角形时a最小,最小值为7····························· 12分 191211212设事件1C 为C 员工答对甲类问题;设事件2C 为C 员工答对乙类问题; 三人得分之和为20分的情况有:①A 员工答对甲类题,答错乙类题;B 与C 员工均答错甲类题,则()()()()()121112110.50.40.40.60.048P A A B C P A P A P B P C ⋅⋅⋅==⨯⨯⨯= ·············································································································· 2分 ②B 员工答对甲类题,答错乙类题;A 与C 员工均答错甲类题,()()()()()121112110.60.50.50.60.09P B B A C P B P B P A P C ⋅⋅⋅==⨯⨯⨯= ·············································································································· 4分 ③C 员工答对甲类题,答错乙类题;A 与B 员工均答错甲类题,()()()()()121112110.40.250.50.40.02P C C A B P C P C P A P B ⋅⋅⋅==⨯⨯⨯=,所以三人得分之和为20分的概率为0.048+0.09+0.02=0.158 ·································· 6分 (2)A 员工得100分的概率为()()()12120.3P A A P A P A ⋅=⋅=,B 员工得100分的概率为()()()12120.3P B B P B P B ⋅=⋅=,C 员工得100分的概率为()()()12120.3P C C P C P C ⋅=⋅=,·············································································································· 9分()~3,0.3X B ∴······················································································ 11分∴()30.30.9E X =⨯= ············································································ 12分20.(12分)(1)取AB 的中点N ,连接MN ,NC ,则线段MN 为三角形SAB 的中位线, MNSA ∴,又,SA BD BD MN ⊥∴⊥ ························································ 2分设直线CN 与直线BD 交于Q 点, 则1,3NQ BQ BNQCDQ NC BD ∆∆∴==,设,,,26AD a CD NC a NQ =∴=∴=∴=,同理,3BD BQ a ==, 2222226325 6(2)分别以直线AD ,AB ,AS 为x 轴,y 轴,z 轴建立直角坐标系,则()()()()()0,0,0,0,0,2,,,A S C B M , 设SP SC λ=,()()()()2,21,2,21P AP λλλλ∴−∴=−································· 8分又()()0,2,1,AM AC ==,设平面AMC 的法向量(),,n x y z =,则(20,2,1,20n AM y z n n AC x ⎧⋅=+=⎪∴=−⎨⋅=+=⎪⎩ ··········································10分 设直线AP 与平面AMC 所成的角为θ,则sin cos ,10AP n θ===, 11,22SP SC λ∴=∴= ·················································································· 12分21.(12分) (1)设1122,MF r MF r ==,在12MF F ∆中,设12F MF θ∠=,22221212122cos 4F F r r r r c θ=+−=,22212122cos 4r r r r c θ∴=+−,又()1212MC MF MF =+, ()()2222222212121212121122cos 4422r r MC MF MF MF MF r r r r c θ∴=++⋅=++=+−,()222121222222122254222r r r r r r MC c c a c +−∴=+−=−=−−=························· 3分 2222229,6,3,3a c a c b ∴−==∴=∴=,22163x y 4 2001122()222221226063x y y t y t x y t λλλ⎧+=⎪⇒+++−=⎨⎪=+⎩, 2121211222226,,,22t t y y y y x y t x y t λλλλλ−∴+=−==+=+++,22121222426,22t t x x x x λλλ−+==++ ································································ 7分 设()()()()()()01020201010201020102y y x x y y x x y y y y x x x x x x x x −⋅−+−⋅−−−+=−−−⋅− ()()()()0001212012201201222x y y x x y y t x y y x x x x x x λ−+++−+=−++ ()()()()20000022202212462x y tx y x t p xx t λλλ+−+−==−+−若p 为常数,则02120tx −= ····································································· 10分 即06tx =,而此时()()()000002200042262y x t x y y x t x x t −==−−−,又06x t<<<<,即t >t <综上所述,t >t <存在点6,A t ⎛ ⎝,使得直线AP 的斜率与直线AQ 的斜率之和为定值02y x t− ············································································ 12分 22.(12分)(1)()()()2221ln ln 1ln ,1x x x x g x x g x x x x−−+'=+=+= ······································ 1分 令()()211ln ,20h x x x h x x '=−+=−+>,即2x >,22 3又()()()min 0,0,02h x h h x g x ⎛⎫'=>∴>∴> ⎪⎪⎝⎭, 所以函数()g x 在()0,+∞上单调递增 ····························································· 5分 (2)不等式ln e ee 0axxa x−−>等价于1e ln 0ax x x ax −−−> 令()()()()111e ln 01e 1ax ax g x x x ax g x ax x x−−=−−>'=+−, ···························· 7分 设()()()11e 1,1e ax ax h x x h x ax −−=−∴'=+,当()10,0x h x a<<−'>, 所以函数()h x 在10,a ⎛⎫−⎪⎝⎭上单调递增,在1,a ⎛⎫−+∞ ⎪⎝⎭上单调递减, ()()2max 11e h x h a a a −⎛⎫∴=−=−+ ⎪⎝⎭,()22max 1e ,e 0a h a a−−<−∴=−+<, 所以函数()g x 在1,a ⎛⎫−+∞ ⎪⎝⎭单调递增,在10,a⎛⎫− ⎪⎝⎭单调递减 ··························· 10分 ()2min 2111e ln 1e g x g a a a −−⎛⎫∴=−=−−− ⎪⎝⎭,令21e t a−=,则()()()()()min1ln 10,1,1g t t t m t t m t t =−−=∈'=−, ()m t ∴在()0,1单调递减,在()1,+∞单调递增, ()()()min 10,0m x m m t ∴==>,()()0 1220。
THUSSAT中学生标准学术能力诊断性测试2023-2024学年高三上学期9月测试数学试题学校:___________姓名:___________班级:___________考号:___________(1)证明:MC BD ⊥;(2)若SA AD ⊥,2SA =,点1010,求SP SC .21.已知椭圆222:1(6x y C b +=上的一点满足MF MF ⋅=参考答案:【详解】中点,连接,AE BE ,,,AB BC BD ABC ABD =∠=∠,≌ABD △,AC AD ∴=,AE ∴π,3BD DBC ∠=,BCD ∴△是边长为,26CD BE =,故选:C 8.DGGB选项A ,函数()f x 在区间,62ππ⎛⎫⎪⎝⎭上单调递减,故GGB故选:BCD.12.ABC【分析】根据斜率是否存在分类设直线距离为定值,即可判断A;∠的平分线根据椭圆的对称性,AOB【详解】AI :如图,作OM AB⊥于M,则点AB斜率不存在时,设直线AB设2AB a =,高PO h =,则2OD a =,在Rt MOD 中,所以正四棱锥的体积13V Sh =2282(4)V h h h h '=-+=--,故当0V '<,函数V 单调递减,因为2SA =,则()0,0,0A 、(S 设平面AMC 的法向量为(m x =则222020m AC x y m AE y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ ,取设()(2,22,22SP SC λλ==-=()(f x>恒成立.即2a-e<-时,不等式()0。
深圳市宝安区2019届高三9月调研考试数学(文科)本试卷满分150分,考试时间120分钟.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数52i -的共轭复数是( ) A .2i + B .2i -+ C .2i -- D .2i -2.已知集合2{|1}M x x ==,{|1}N x ax ==,若N M ⊆,则实数a 的取值集合为( )A .{1}B .{1,1}-C .{1,0}D .{1,1,0}- 3. 定义某种运算:S m n ⊗=⊗的运算原理如右边的流程图所示,则6547⊗-⊗=( )A.3B.1C.4D. 04.某景区在开放时间内,每个整点时会有一趟观光车从景区入口发车,某人上午到达景区入口,准备乘坐观光车,则他等待时间不多于10分钟的概率为( ) A .110B .16C .15D .565.已知函数2lg(54)y x x =++的零点是1tan x α=和2tan x β=,则tan()αβ+=( ) A .53B .53-C .52D .52-6.若实数a ,b 满足1a b >>,log (log )a a m b =,2(log )a n b =,2log a l b =,则m ,n ,l 的大小关系为( )A .m l n >>B .l n m >>C .n l m >>D .l m n >> 7. 在ABC ∆中,“tan tan 1B C >”是“ABC ∆为锐角三角形”的( )A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既不充分也不必要条件 8.为美化环境,从黄、白、红、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率为( )A .12 B .13 C .56 D .239. 若实数x ,y 满足||||2x y +≥,则222M x y x =+-的最小值为( )A .2-B .0C .21- D .12- 10. 如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=,1AB AD ==. 若点E 为边CD 上的动点,则AE BE ⋅的最小值为 ( )A.2116 B. 32 C. 2516D. 3 11.函数()2sin()(0)3f x x πωω=+>的图象在[0,1]上恰有两个最大值点,则ω的取值范围为( )A .[2,4]ππB .9[2,)2ππ C .1325[,)66ππ D .25[2,)6ππ 12. 已知,,A F P 分别为双曲线22221(0,0)x y a b a b-=>> 的左顶点、右焦点以及右支上的动点,若2PFA PAF ∠=∠恒成立,则双曲线的离心率为( ) A. 2 B. 3 C. 2 D. 13+二、填空题:本题共4小题,每小题5分,共20分. 13.已知2)4πtan(-=+α,则=-αα2cos 2sin 114.过双曲线2222:1(,0)x y E a b a b-=>的右焦点,且斜率为2的直线与E 的右支有两个不同的公共点,则双曲线离心率的取值范围是________.15.《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为 直角三角形的四面体).在如图所示的堑堵111C B A ABC - 中,4,3,51====BC AB AC AA ,则阳马111A ABB C -的外接球的表面积是16.定义在R 上的函数()f x 满足()()f x f x -=,且当0x ≥21,01,()22,1,xx x f x x ⎧-+≤<=⎨-≥⎩ 若任意的[],1x m m ∈+,不等式(1)()f x f x m -≤+恒成立,则实数m 的最大值是三、解答题:共70分。
2018-2019学年四川省高三(上)9月联考数学试卷(文科)一、选择题.1.已知集合{}1,2,3,4A =,{}32,B y y x x A ==-∈,则A B =( ) A .{}1B .{}4C .{}1,3D .{}1,42.复数()1i i ⋅+( ) A .1i +B .1i -C .1i -+D .1i --3.若函数()f x 的定义域是[]1,1-,则()sin f x 的定义域为( ) A .RB .[]1,1-C .,22ππ⎡⎤-⎢⎥⎣⎦D .[]sin1,sin1-4.已知角α的终边上一点坐标为55sin ,cos 66ππ⎛⎫ ⎪⎝⎭,则角α的最小正值为( ) A .56πB .116πC .53π D .23π 5.函数()sin cos f x x x =-的最小正周期为( ) A .2πB .32π C .π D .2π 6.与直线3450x y -+=关于x 轴对称的直线的方程是( )A .3450x y -+=B .3450x y --=C .3450x y +-=D .3450x y ++= 7.由直线1y x =+上的一点向圆()2231x y -+=引切线,则切线长的最小值为( ) A .1B .22C .7D .38.函数22x y x =-的图象大致是( )A .B .C.D.9.已知双曲线()222:103x y C a a -=>的右焦点为F ,则点F 到C 的渐近线的距离为( ) A .3 B .3 C .a D .3a10.若函数()ln f x a x x =+有两个零点,则实数a 的取值范围为( )A .10,e ⎡⎤⎢⎥⎣⎦B .10,e ⎛⎫ ⎪⎝⎭C .10,e ⎛⎤ ⎥⎝⎦D .1,0e ⎛⎫- ⎪⎝⎭11.已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若AB =3,AC =4,AB AC ⊥,AA 1=12,则球O 的半径为( ) A .3172B .210C .132D .31012.若()f x 函数满足()()22f x f x +=,当()0,2x ∈时,()1ln 2f x x ax a ⎛⎫=-> ⎪⎝⎭,当()4,2x ∈--时,()f x 的最大值为14-,则实数a 的值为( )A .3B .eC .2D .1二、填空题.13.已知1a =,2b =,向量a 与的b 夹角大小为60°,若ma b +与2a b -垂直,则实数m = .14.设函数()()211log 2,12,1x x x f x x -⎧+-<⎪=⎨≥⎪⎩,则()()22log 12f f -+= .15.设变量x ,y 满足约束条件3602030x y x y y +-≥⎧⎪--≤⎨⎪-≤⎩,则目标函数2z y x =-的最小值为 .16.已知函数()3sin f x x x x =+-则满足不等式()()2120f m f m -+≤成立的实数m 的取值范围是 . 三、解答题.17.等差数列{}n a 中,34574,6a a a a +=+=. (1)求{}n a 的通项公式.(2)记n S 为{}n a 的前项和,若12m S =,求m .18.某火锅店为了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y (单位:千元)与该地当日最低气温x (单位:℃)的数据,如表:x 2 5 8 9 11 y1210887(1)求y 关于x 的回归方程ˆˆˆybx a =+; (2)判定y 与y 之间是正相关还是负相关,若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额.19.如图,在多面体ABCDEF 中,四边形ABCD 是矩形,四边形ABEF 为等腰梯形,且//,2442AB EF AF AB AD ===,平面ABCD ⊥平面ABEF(1)求证:BE ⊥DF ;(2)求三棱锥C ﹣AEF 的体积V .20.已知点A ,B 分别是椭圆2213620x y +=的左右顶点,点F 是椭圆的右焦点,点P 在椭圆上位于x 轴上方,且满足PA ⊥PF . (1)求点P 的坐标;(2)设点M 是椭圆长轴AB 上的一点,点M 到直线AP 的距离等于MB ,求M 点的坐标. 21.已知函数()32ln 2,f x x x ex ax a R =-+-∈,其中e 为自然对数的底数. (1)若()()f x f x 的图象在x e =处的切线斜率为2,求a ; (2)若()f x 有两个零点,求a 的取值范围.考生从所给的第22题、23题两题中任选一题作答(答题前务必用2B 铅笔将所选做题的方框涂黑)22.在平面直角坐标系xOy 中,已知曲线11:12x t C y t =+⎧⎨=-⎩(t 为参数)与曲线2cos :3sin x a C y θθ=⎧⎨=⎩(θ为参数,0a >).(Ⅰ)若曲线1C 与曲线2C 有一个公共点在x 轴上,求a 的值;(Ⅱ)当a =3时,曲线1C 与曲线2C 交于A ,B 两点,求A ,B 两点的距离.23.已知定义在R 上的函数(),*f x x m x m N =-+∈,若存在实数x 使()2f x <成立. (1)求实数m 的值;(2)若1a >,1b >,()()4f a f b +=,求证:413a b+>.2018-2019学年四川省高三(上)9月联考数学试卷(文科)参考答案与试题解析一、选择题.1.【分析】把A 中元素代入32y x =-中计算求出y 的值,确定出B ,找出A 与B 的交集即可.【解答】解:把x =1,2,3,4分别代入32y x =-得:y =1,4,7,10,即{}1,4,7,10B =, ∵{}1,2,3,4A =, ∴{}1,4A B =, 故选:D .【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键. 2.【分析】利用复数的运算即可得出. 【解答】解:原式21i i i =+=-+. 故选:C .【点评】熟练掌握复数的运算法则是解题的关键.3.【分析】根据()f x 的定义域为[]1,1-即可得出,()sin f x 满足1sin 1x -≤≤,而对任意的x R ∈都有1sin 1x -≤≤,从而得出()sin f x 的定义域为R . 【解答】解:∵()f x 的定义域是[]1,1-;∴()sin f x 满足1sin 1x -≤≤; ∴x R ∈;∴()sin f x 的定义域为R . 故选:A .【点评】考查函数定义域的概念及求法,已知()f x 定义域求()f g x ⎡⎤⎣⎦定义域的方法,以及正弦函数的定义域.4.【分析】由条件利用任意角的三角函数的定义,求得1cos 2α=,且3sin 2α=-,可得α的最小正值.【解答】解:角α的终边上一点坐标为55sin ,cos 66ππ⎛⎫ ⎪⎝⎭,而该点13,22⎛⎫- ⎪ ⎪⎝⎭在第四象限, 且满足1cos 2α=,且3sin 2α=-,故α的最小正值为53π,故选:C .【点评】本题主要考查任意角的三角函数的定义,属于基础题.5.【分析】利用了函数()sin y A x ωϕ=+的最小正周期为122πω⋅,得出结论.【解答】解:函数()sin cos 2sin 4f x x x x π⎛⎫=-=- ⎪⎝⎭|的最小正周期为1221ππ⋅=, 故选:C .【点评】本题主要考查函数()sin y A x ωϕ=+的周期性,利用了函数()sin y A x ωϕ=+为函数()sin y A x ωϕ=+的周期性的一半,属于基础题.6.【分析】设出所求对称直线上的点的坐标,求出关于x 轴的对称点坐标,代入已知直线方程,即可.【解答】解:设所求对称直线的点的坐标(x ,y ),关于x 轴的对称点的坐标(x ,﹣y )在已知的直线上,所以所求对称直线方程为:3450x y ++=. 故选:D .【点评】本题是基础题,考查直线关于直线的对称直线方程的求法,考查计算能力,常考题型,注意特殊直线为对称轴的情况,化简解题过程.7.【分析】先求圆心到直线的距离,此时切线长最小,由勾股定理不难求解切线长的最小值.【解答】解:切线长的最小值是当直线1y x =+上的点与圆心距离最小时取得,圆心(3,0)到直线的距离为301222d -+==,圆的半径为1,故切线长的最小值为22817d r -=-=, 故选:C .【点评】本题考查圆的切线方程,点到直线的距离,是基础题.8.【分析】根据函数图象的交点的个数就是方程的解的个数,也就是y =0,图象与x 轴的交点的个数,排除BC ,再取特殊值,排除D【解答】解:分别画出函数()2x f x =(红色曲线)和()2g x x =(蓝色曲线)的图象,如图所示,由图可知,()f x 与()g x 有3个交点, 所以3220y x x =-=,有3个解,即函数22x y x =-的图象与x 轴由三个交点,故排除B ,C , 当x =﹣3时,()23230y -=--<,故排除D 故选:A .【点评】本题主要考查了函数图象的问题,关键是理解函数图象的交点和方程的解得个数的关系,排除是解决选择题的常用方法,属于中档题9.【分析】求出双曲线的右焦点坐标,渐近线方程,利用已知条件求解即可.【解答】解:双曲线()222:103x y C a a -=>的右焦点为F (c ,0),点F 到渐近线3y x a =的距离为:23333c cb ca ===+, 故选:B .【点评】本题考查双曲线的简单性质的应用,是基础题.10. 【分析】求导()'ln 1f x x =+,从而可得()f x 在10,e ⎛⎫ ⎪⎝⎭上是减函数,在1,e ⎛⎫+∞ ⎪⎝⎭上是增函数,结合函数在定义域内的极限,可得函数()ln f x a x x =+有两个零点时,实数a 的取值范围.【解答】解:∵函数()ln f x a x x =+有两个零点, ∴函数()'ln 1f x x =+,当10,x e ⎛⎫∈ ⎪⎝⎭时,()'0f x <,函数为减函数;当1,x e ⎛⎫∈+∞ ⎪⎝⎭时,()'0f x >,函数为增函数;故当1x e =时,函数取最小值1a e-,又∵()0lim x f x a +→=,()lim x f x →+∞=+∞; ∴若使函数()f x 有两个零点,则0a >且10a e -<,即10,a e ⎛⎫∈ ⎪⎝⎭,故选:B .【点评】本题考查了导数法求函数的最小值,函数的零点,对数函数的图象和性质,属于中档题11.【分析】通过球的内接体,说明几何体的侧面对角线是球的直径,求出球的半径.【解答】解:因为三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,所以三棱柱的底面是直角三角形,侧棱与底面垂直,侧面11B BCC ,经过球的球心,球的直径是其对角线的长,因为AB =3,AC =4,BC =5,BC 1=225+12=13, 所以球的半径为:132. 故选:C .【点评】本题考查球的内接体与球的关系,球的半径的求解,考查计算能力. 12【分析】由已知得:()()()112424f x f x f x =+=+,设()4,2x ∈--时,则()40,2x +∈,代入可得()()()()1114ln 44444f x f x x a x =+=+-+,再根据当()4,2x ∈--时,()f x 的最大值为14-,利用导数求得它的最大值,解方程即可求得a 的值,进而求得结论;【解答】解:由已知得:()()()112424f x f x f x =+=+, 当()0,2x ∈时,()1ln 2f x x ax a ⎛⎫=-> ⎪⎝⎭,设()4,2x ∈--时,则()40,2x +∈, ∴()()()4ln 44f x x a x +=+-+ ∴()4,2x ∈--时,()()()()1114ln 44444f x f x x a x =+=+-+ ∴()()()()()114141'4444444x a x a a a f x x x x ⎛⎫+- ⎪-+⎝⎭=-==-+++, ∵12a >, ∴142a->, ∴142a ⎛⎫--<- ⎪⎝⎭,∴当144x a-<<-时,()'0f x >,函数()f x 单调递增, 当142x a-<<-时,()'0f x <,函数()f x 单调递减, ∴()max 1111114ln 444f x f a a a a⎛⎫⎛⎫=-=-⋅=- ⎪ ⎪⎝⎭⎝⎭,∴a =1, 故选:D .【点评】考查函数解析式的求法以及函数恒成立问题,体现了转化和分类讨论的思想方法,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力. 二、填空题.13.【分析】利用向量垂直的充要条件可解决此问题. 【解答】解:根据题意得,()()20ma b a b +⋅-=, ∴()222120ma m a b b --⋅=-=而11212a b ⋅=⨯⨯= ∴2180m m -+-= ∴7m =- 故答案为﹣7.【点评】本题考查向量的夹角,向量垂直的充要条件.14.【分析】由条件利用指数函数、对数函数的运算性质,求得()()22log 12f f -+的值.【解答】解:由函数()()211log 2,12,1x x x f x x -⎧+-<⎪=⎨≥⎪⎩,可得()()()()()22log 121log 6222log 121log 42122369f f --+=++=++=+=, 故答案为:9.【点评】本题主要考查分段函数的应用,指数函数、对数函数的运算性质,求函数的值,属于基础题.15.【分析】作出题中不等式组表示的平面区域,得如图的△ABC 及其内部,再将目标函数2z y x =-对应的直线进行平移,可得当x =5且y =3时z 取得最小值,可得答案.【解答】解:作出不等式组3602030x y x y y +-≥⎧⎪--≤⎨⎪-≤⎩表示的平面区域,得到如图的△ABC 及其内部,其中A (3,3),B (5,3),C (2,0,) 设(),2z F x y y x ==-,将直线:2l z y x =-进行平移,观察y 轴上的截距变化,可得当l 经过点B 时,目标函数z 达到最小值 ∴()5,37z F ==-最小值 故答案为:﹣7【点评】本题给出二元一次不等式组,求目标函数2z y x =-的最小值,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.16.【分析】利用导数判断原函数为定义域上的增函数,再由奇偶性定义判断为奇函数,把原不等式转化为关于m 的一元二次不等式求解.【解答】解:由()3sin f x x x x =+-,得()2'31cos 0f x x x =+-≥, ∴函数()f x 为增函数,又()()()()()33sin sin f x x x x x x x f x -=----=-+-=-,∴()f x 为奇函数.由()()2120f m f m -+≤,得()()212f m f m -≤- 即212m m -≤-,∴2210m m +-≤. 解得112m -≤≤. 故答案为:11,2⎡⎤-⎢⎥⎣⎦.【点评】本题考查利用导数研究函数的单调性,考查函数单调性与奇偶性的应用,是中档题.三、解答题.17. 【分析】(1)结合等差数列的通项公式及已知条件可求1a ,d ,进而可求n a , (2)由(1)结合等差数列的求和公式n S ,结合已知可求m 【解答】解:(1)等差数列{}n a 的公差为d , ∵34574,6a a a a +=+=,∴1125453a d a d +=⎧⎨+=⎩, 解方程可得,1a =1,25d =, ∴()2231155n n a n +=+-=; (2)由(1)可知,()()142255n n n n n S n -+=+⨯=, 由12m S =,可得,()4125m m +=, ∴m =6或m =﹣10(舍). 故m =6.【点评】本题主要考查了等差数列的通项公式及求和公式的简单应用,属于基础试题. 18. 【分析】(1)根据回归系数公式计算回归系数,得出回归方程; (2)将x=6代入回归方程计算估计值.【解答】解:(1)()125891175x =⨯++++=,()1121088795y =⨯++++=.5214256481121295ii x==++++=∑,512450647277287i ii x y==++++=∑,∴287579ˆ0.56295572b-⨯⨯==--⨯, ()ˆ90.56712.92a=--⨯=. ∴回归方程为:ˆ0.5612.92yx =-+.(2)∵ˆ0.560b=-<,∴y 与x 之间是负相关. 当x =6时,ˆ0.56612.929.56y=-⨯+=. ∴该店当日的营业额约为9.56千元.【点评】本题考查了线性回归方程的求解,利用回归方程进行数值估计,属于基础题. 19.【分析】(1)取EF 的中点G ,连结AG ,推导出四边形ABEG 为平行四边形,AG ∥BE ,且AG=BE=AF =2,再求出AG ⊥AF ,AD ⊥AB ,从而AD ⊥平面ABEF ,AD ⊥AG ,进而AG ⊥平面ADF ,再由AG ∥BE ,得BE ⊥平面ADF ,由此能证明BE ⊥DF ;(2)首先证明CD ∥平面ABEF ,可得C AEF D AEF V V --=,由(1)得DA ⊥平面ABEF ,再求出三角形AEF 的面积,代入棱锥体积公式得答案. 【解答】(1)证明:取EF 的中点G ,连结AG , ∵EF =2AB ,∴AB =EG ,又AB ∥EG ,∴四边形ABEG 为平行四边形, ∴AG ∥BE ,且AG =BE =AF =2,在△AGF 中,GF =1222EF =,AG =AF =2,∴222AG AF GF +=,∴AG ⊥AF , ∵四边形ABCD 是矩形,∴AD ⊥AB ,又平面ABCD ⊥平面ABEF ,且平面ABCD 平面ABEF =AB , ∴AD ⊥平面ABEF ,又AG ⊂平面ABEF , ∴AD ⊥AG , ∵ADAF=A ,∴AG ⊥平面ADF ,∵AG ∥BE ,∴BE ⊥平面ADF , ∵DF ⊂平面ADF ,∴BE ⊥DF ;(2)解:∵CD ∥AB 且CD ⊄平面ABEF ,BA ⊂平面ABEF , ∴CD ∥平面ABEF , ∴C AEF D AEF V V --=,由(1)得,DA ⊥平面ABEF ,∵142242AEF S ∆=⨯⨯=,∴1424233C AEFD AEF V V --==⨯⨯=.【点评】本题考查线线垂直的证明,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.20. 【分析】(1)先求出PA 、F 的坐标,设出P 的坐标,求出,PA PF 的坐标,由题意可设点P (m ,n ),则()()6,,4,AP m n FP m n =+=-.由题意可得()2221,603620m n m m n +=++=,且0n >,解得32m =,即可求得点P 的坐标. (2)求出直线AP 的方程,设点M 的坐标,由M 到直线AP 的距离等于MB ,求出点M 的坐标.【解答】解:(1)由已知可得点A (﹣6,0),F (4,0), 设点(),P m n ,则()()6,,4,AP m n FP m n =+=-.由题意可得()2221,603620m n m m n +=++=,且0n >, 化为229180m m +-=,解得32m =,或6m =-. 由于0n >,只能32m =,于是532n =.∴点P 的坐标是353,22⎛⎫⎪ ⎪⎝⎭.(2)直线AP 的方程是360x y -+=.设点(),0M m ,则M 到直线AP 的距离是62m +.于是662m m +=-,又66m -≤≤,解得m =2, 故点M (2,0).【点评】本题考查椭圆的简单性质和点到直线的距离公式,两个向量垂直的性质,求出点M 的坐标,是解题的难点.21. 【分析】(1)求出函数的导数,计算()'f e ,求出a 的值即可; (2)求出2ln 2x x ex a x -+=,记()2ln 2xF x x ex x=-+,根据函数的单调性求出()F x 的最大值,从而求出a 的范围即可. 【解答】解:(1)()21'34f x x ex a x=-+-, ()21'2f e e a e=+-=,∴212a e e=--.(2)由32ln 20x x ex ax -+-=, 得2ln 2xx ex a x-+=, 记()2ln 2xF x x ex x=-+, 则()()1ln '2xF x x e x-=--, (),x e ∈+∞,()'0F x <,()F x 递减;()0,x e ∈时,()'0F x >,()F x 递增.∴()()2max 1F x F e e e==+.而x →0时()F x →-∞,x →+∞时()F x →-∞,故21a e e<+.【点评】本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.考生从所给的第22题、23题两题中任选一题作答(答题前务必用2B 铅笔将所选做题的方框涂黑)22. 【分析】(I )曲线C 1:112x t y t =+⎧⎨=-⎩(t 为参数),化为:32y x =-.令y =0可得与x 轴的交点.曲线C 2:cos 3sin x a y θθ=⎧⎨=⎩(θ为参数,0a >)的直角坐标方程为:22219x y a +=.利用y =0可得与x 轴的交点.(II )当a =3时,曲线C 2:cos 3sin x a y θθ=⎧⎨=⎩化为:229x y +=.利用点到直线的距离公式可得:圆心到直线的距离d .利用弦长公式可得222AB r d =-.【解答】解:(I )曲线C 1:112x t y t =+⎧⎨=-⎩(t 为参数),化为:32y x =-.与x 轴的交点为3,02⎛⎫⎪⎝⎭. 曲线C 2:cos 3sin x a y θθ=⎧⎨=⎩(θ为参数,0a >)的直角坐标方程为:22219x y a +=.与x 轴的交点为(±a ,0). ∵0a >,∴32a =. (II )当a =3时,曲线C 2:cos 3sin x a y θθ=⎧⎨=⎩化为:229x y +=.圆心到直线的距离33555d ==. ∴2223512522955AB r d ⎛⎫=-=-= ⎪ ⎪⎝⎭.【点评】本题考查了极坐标方程化为直角坐标方程、点到直线的距离公式、圆的标准方程及其应用、弦长公式,考查了推理能力与计算能力,属于中档题.23. 【分析】(1)要使不等式2x m x -+<有解,则2m <,再由*m N ∈,能求出实数m 的值.(2)先求出3αβ+=,从而()411413αβαβαβ⎛⎫+=++ ⎪⎝⎭,由此利用基本不等式能证明:413αβ+>.【解答】解:(1)因为()x m x x m x m -+≥--=.…(2分) 要使不等式2x m x -+<有解,则2m <,解得22m -<<.…(4分) 因为*m N ∈,所以1m =.…(5分)证明:(2)因为,1αβ>,所以()()21214f f αβαβ+=-+-=,则3αβ+=.…(6分) 所以()41141141455+2=3333βαβααβαβαβαβαβ⎛⎫⎛⎫⎛⎫+=++=++≥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.… (当且仅当4=βααβ,即=2α,1β=时等号成立)…(9分) 又因为,1αβ>,所以413αβ+>恒成立.故413αβ+>.…【点评】本题考查实数值的求法,考查不等式的证明,是中档题,解题时要认真审题,注意基本不等式性质的合理运用.。