重庆大学材料力学答案
- 格式:doc
- 大小:3.83 MB
- 文档页数:72
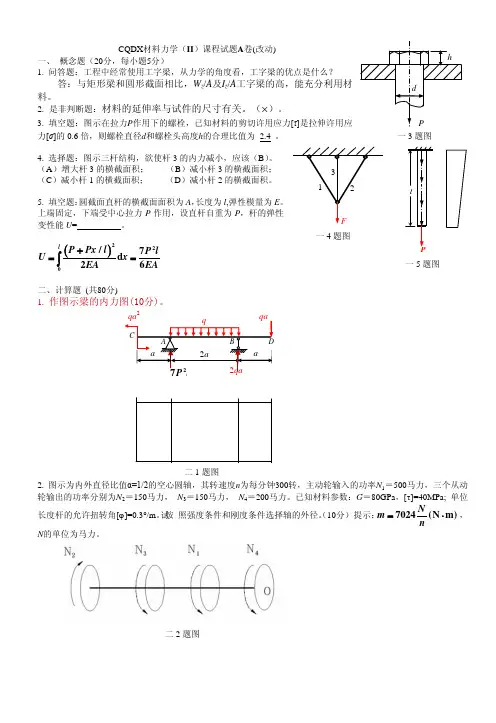
重庆大学材料力学课程试题(A 卷)一、作简支梁的内力图。
(20 分)题 1 图解:1. 计算支座反力.将梁上的载荷向梁的中点简化,简化结果为一集中力偶:m = 32KN ⋅m (逆时针)支座反力:RA 2. 作内力图=32=4KN(↑),R8 B=32= 4KN (↓)8根据支座反力及载荷作剪力图及弯矩图。
Q (KN)M (KN•m)二、简支梁AB 和悬臂梁DH 用直杆CH 相联。
C 点和H 点均为铰接,H 点承受垂直载荷P 的作用。
已知梁AB 和DH 的抗弯刚度为EI,杆CH 的抗拉刚度为EA,试求杆CH 的轴力及点H 的垂直位移。
(20 分)1 3解:1. 静不定次数确定 题 2 图m = 3, n = 2, r = 6结构的自由度 2. 分析计算D = 3m - 2n - r = 3⨯ 3 - 2 ⨯ 2 - 6 = -1 1 次静不定结构 去掉二力杆 CH ,即可得到基本结构,设 CH 杆轴向拉力为 N ,梁的挠度δ C 、 δ H 以向下为正,则变形集合条件为: δ H - δ C = ⊗l CH (1)δ= (P - N )a 3 H 3EI = N (2a )3 C 48EI , ⊗l C H =NaEA代入式(1),得:(P - N )a 3 -N (2a )3= Na3EI 由此式解出: 48EI N =EA2Pa 2 A3(2I + a 2 A )代入δ H ,即得 H 点的垂直位移为:δ =Pa 3 6I + a 2 AH 9EI ( 2I + a 2A )三、 直径为 20mm 的圆截面平面折杆ADBC 在C 点受竖向力P 的作用,∠ABC =90 度,杆的弹性模量E=200Gpa ,泊松比μ=0.3,现由实验测得D 点截面处的顶部表面的主应变ε =508×10-6, ε =-288×10-6,试确定外力P 及BC 段的长度a 的大小。
已知l =314mm 。
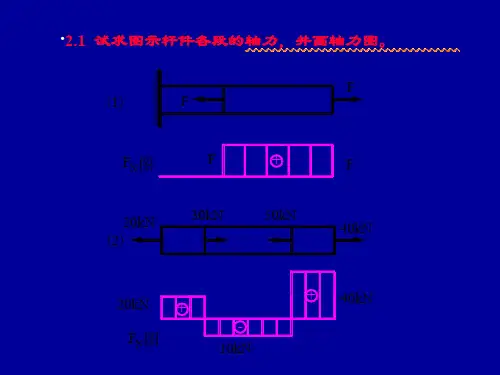
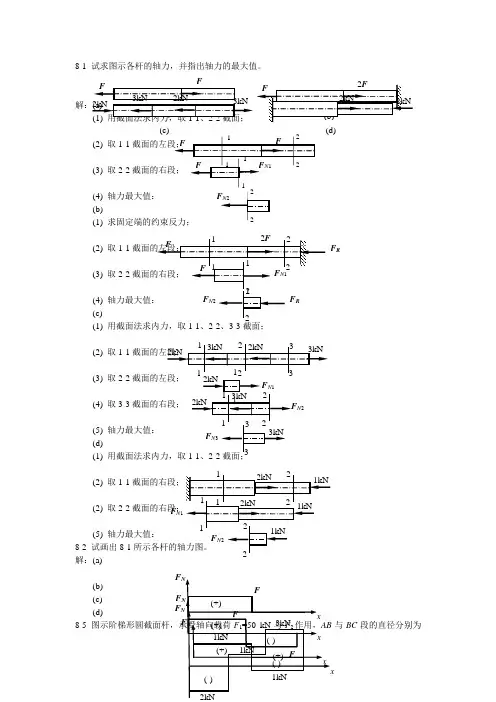
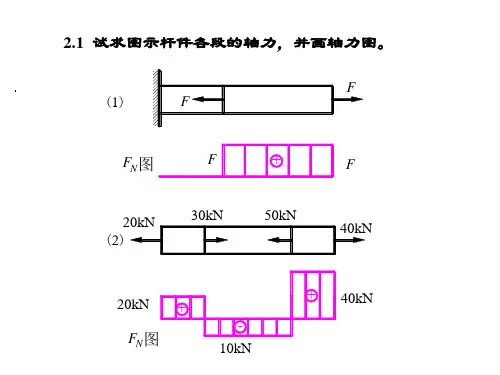
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。


绪论一、是非题1.1材料力学主要研究杆件受力后变形与破坏的规律。
()1.2内力只能是力。
()1.3若物体各点均无位移,则该物体必定无变形。
()1.4截面法是分析应力的基本方法。
()二、选择题1.5构件的强度是指(),刚度是指(),稳定性是指()A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持其原有的平衡状态的能力C.在外力作用下构件抵抗破坏的能力1.6根据均匀性假设,可认为构件的()在各点处相同。
A.应力B.应变C.材料的弹性常数D.位移1.7下列结论中正确的是()A.内力是应力的代数和B.应力是内力的平均值C.应力是内力的集度D.内力必大于应力参考答案:1.1 V 1.2 X 1.3 V 1.4 X 1.5 C,A,B 1.6 C 1.7 C轴向拉压、选择题1.等截面直杆CD位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD两侧的摩擦力沿轴线方向均匀分布,且两侧摩擦力的集度均为q,杆CD的横截面面积为A,质量密度为,试问下列结论中哪一个是正确的?(A)q = -gA;(B)杆内最大轴力F zmax =ql ;(C)杆内各横截面上的轴力F N = P ~~;——2(D)杆内各横截面上的轴力F N =0。
2.低碳钢试样拉伸时,横截面上的应力公式c -F N A适用于以下哪一种情况(A)只适用于二<c p; (B)只适用于二w :二e;(C)只适用于二w二s ;(D)在试样拉断前都适用。
3.在A和B两点连接绳索ACB,绳索上悬挂物重P,如图示。
点A和点B的距离保持不变,绳索的许用拉应力为[二]。
试问:当:-角取何值时,绳索的用料最省?(A) 0’ ;(B) 30’ ;(C) 45」; (D) 60」。
4.桁架如图示,载荷F可在横梁(刚性杆)DE上自由移动。
杆1和杆2的横截面面积均为A,许用应力均为[二](拉和压相同)。
求载荷F的许用值。
以下四种答案中哪一种是正确的?(A)(C)[匚]A ;5. 设受力在弹性范围内,问空心圆杆受轴向拉伸时,夕卜径与壁厚的下列四种变形关系中哪一种是正确的?(A)外径和壁厚都增大; (B)外径和壁厚都减小;(C)外径减小,壁厚增大;(D)外径增大,壁厚减小。

材料力学重庆大学智慧树知到答案2024年第一章测试1.变形固体的基本假设是()。
A:连续、均匀性假设和线性弹性假设; B:线性弹性假设和小变形假设; C:连续、均匀性假设和各向同性假设; D:各向同性假设、小变形假设和线性弹性假设。
答案:C2.要使构件安全、正常地工作,必须满足()。
A:稳定性要求 B:强度要求、刚度要求、稳定性要求 C:强度要求 D:强度要求和稳定性要求答案:B第二章测试1.应力是指截面上每点处单位面积内的分布内力,即内力集度。
()A:错 B:对答案:B2.构件中不同点处的线应变及切应变一般是不同的,而且线应变与正应力相对应,切应变与切应力相对应。
()A:错 B:对答案:B3.等直杆发生拉(压)变形时,横截面上各点既有正应力,又有切应力。
()A:错 B:对答案:A4.等直杆受力如图,该杆的轴力最大值为()。
A:2kN B:4kN C:5kN D:3kN 答案:D5.等直杆受力如图,其上端截面的轴力为()。
A:F+ql B:-F+ql C:F D:ql答案:B第三章测试1.等直杆受力如图,该杆的扭矩最大值为()。
A:6kN.m B:2kN.m C:4kN.m D:8kN.m答案:C2.等截面圆轴配置四个皮带轮,各轮传递的力偶的力偶矩如图所示。
从抗扭的角度如何改变四个轮之间的相对位置,轴的受力最合理的是()。
A:将B轮与C轮对调 B:将B轮与D轮对调, 然后再将B轮与C轮对调 C:将C轮与D轮对调 D:将B轮与D轮对调答案:C3.内外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内圆周上各点的切应力为()。
A:τ B:零C:ατ D:答案:C4.一圆轴用普通碳素钢制成,受扭后发现单位长度扭转角超过了许用值,为提高刚度拟采用的合理措施是()A:用铸铁代替 B:改为优质合金钢 C:减少轴的长度 D:增大轴的直径答案:D5.下述结论中,正确的是()A:若物体内各点的应变均为零, 则物体无位移 B:应变分为线应变和切应变, 其量纲为长度 C:若物体的各部分均无变形, 则物体内各点的应变为零 D:受拉杆件全杆的轴向伸长,标志着杆件内各点的变形程度答案:C第四章测试1.悬臂梁受力如图,以下说法正确的是()。



重庆大学材料力学(II )课程试题A 卷一、 问答题(20分,每小题5分)1、在推导材料力学的某些基本理论和方法时,需要作一些必要的假设。
试列举其中的三个假设。
答:略;2、对于低碳钢,何谓 P σ? 答:比例极限;3、工程中经常使用工字梁,从力学的角度看,工字梁的优点是什么? 答:与矩形梁和圆形截面相比,工字梁的高,能充分利用材料。
A W z /4、图示为材料相同、长度相等的等截面圆杆和变截面圆杆,试问哪一种杆件承受冲击的能力强?简述理由。
(a ) (b )答:不好定性判别。
因为a 杆的动载系数小于b 杆的动载系数,但a 杆的静应力大于b 杆的静应力。
二、 图示为内外直径比值2/1=α的空心圆轴,其转速度n 为每分钟300转,主动轮输入的功率N 1=500马力,三个从动轮输出的功率分别为N 2=150马力, N 3=150马力, N 4=200马力。
已知材料参数:G =80Gpa ,[]MPa 40=τ;单位长度杆的允许扭转角[]m /3.0o =ϕ。
试按照强度条件和刚度条件选择轴的外径。
(15)提示:)(7024m N nNm ⋅=,N 的单位为马力。
解: 计算作用于各轮上的外力偶矩:m N n N m .1117003005007024702411=×==; m N nN m m .35127024232===; m N m .468030020070244=×= 作扭矩图:可见: m N .7024max =τ 由强度条件: ][)1(1643maxmax max ταπτ≤−==D T W T t得: m T D 0984.01040)5.01(702416])[1(1636434max =××−××=−≥πταπ 由刚度条件: ][180max max ϕπϕ≤×=p GI T 得: m G T D 1162.0])[1(18032442max =−×≥ϕαπ 取轴得直径为: D =120mm三、 一矩形截面梁如图所示,已知kN P 10=,m a 2.1=;材料的许用应力MPa 10][=σ.设梁的高宽比2/=b h 。
重庆大学材料力学答案题图所示中段开槽的杆件,两端受轴向载荷P 的作用,试计算截面1-1和2-2上的应力。
已知:P = 140kN ,b = 200mm ,b 0 = 100mm ,t = 4mm 。
题图解:(1) 计算杆的轴力 (2) 计算横截面的面积 (3) 计算正应力(注:本题的目的是说明在一段轴力相同的杆件内,横截面面积小的截面为该段的危险截面)横截面面积A=2cm 2的杆受轴向拉伸,力P=10kN ,求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ,并问m ax τ发生在哪一个截面? 解:(1) 计算杆的轴力(2) 计算横截面上的正应力 (3) 计算斜截面上的应力(4) m ax τ发生的截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此:22πα=, ο454==πα故:m ax τ发生在其法线与轴向成45°的截面上。
(注:本题的结果告诉我们,如果拉压杆处横截面的正应力,就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°的截面上,最大正应力发生在横截面上,横截面上剪应力为零)题图所示阶梯直杆AC ,P =10kN ,l 1=l 2=400mm ,A 1=2A 2=100mm 2,E =200GPa 。
试计算杆AC 的轴向变形Δl 。
题图解:(1) 计算直杆各段的轴力及画轴力图 kN 101==P N (拉) kN 102-=-=P N (压)(2) 计算直杆各段的轴向变形mm 2.010010002004001000101111=⨯⨯⨯⨯==∆EA l N l (伸长)mm 4.05010002004001000102222-=⨯⨯⨯⨯-==∆EA l N l (缩短) (3) 直杆AC 的轴向变形m m 2.021-=∆+∆=∆l l l (缩短)(注:本题的结果告诉我们,直杆总的轴向变形等于各段轴向变形的代数和)题图所示结构,各杆抗拉(压)刚度EA 相同,试求节点A 的水平和垂直位移。
重庆大学材料力学答案2.9 题图2.9所示中段开槽的杆件,两端受轴向载荷P 的作用,试计算截面1-1和2-2上的应力。
已知:P = 140kN ,b = 200mm ,b 0 = 100mm ,t = 4mm 。
题图2.9解:(1) 计算杆的轴力 kN 14021===P N N (2) 计算横截面的面积21mm 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注:本题的目的是说明在一段轴力相同的杆件内,横截面面积小的截面为该段的危险截面)2.10 横截面面积A=2cm 2的杆受轴向拉伸,力P=10kN ,求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ,并问m ax τ发生在哪一个截面? 解:(1) 计算杆的轴力kN 10==P N(2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ(3) 计算斜截面上的应力MPa 5.37235030cos 2230=⎪⎪⎭⎫ ⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生的截面 ∵0)2c o s (==ασαταd d 取得极值 ∴ 0)2c o s (=α 因此:22πα=, 454==πα故:m ax τ发生在其法线与轴向成45°的截面上。
(注:本题的结果告诉我们,如果拉压杆处横截面的正应力,就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°的截面上,最大正应力发生在横截面上,横截面上剪应力为零)2.17 题图2.17所示阶梯直杆AC ,P =10kN ,l 1=l 2=400mm ,A 1=2A 2=100mm 2,E =200GPa 。
重庆大学2021年考研材料力学真题一、单项选择题(每题只有一个正确答案。
每小题3分,共21分)。
1、建立平面弯曲的正应力公式??m?yiz时,“平截面假设”起到的作用有下列四种答案:(a)“平面截面假设”给出了截面上的内力和应力之间的关系,M?(b)“平面截面假设”给出了梁弯曲的变形规律;(c)“平面截面假设”简化了物理方程;(d)“平面截面假设”是建立胡克定律的基础。
??yda;A正确答案是:2。
当非对称薄壁截面梁承受横向外力时,如果要求梁产生平面弯曲而不产生扭转,则横向外力条件有四个答案:(a)作用面与形心主惯性面重合;(b)作用面与形心主惯性面平行;(c)通过弯曲中心的任意平面;(d)通过弯曲中心并平行于主惯性面。
正确答案是:3、梁ab的杆端约束分别如图示三种情况,它们所承受的自由落体冲击荷载相同,关于其动应力的下列结论中:phpakkhaeicbaeicbeicbk(a)(a)>(b)>(c);(b)(b)>(a)>(c);(c)(c)>(b)>(a);(d)(a)=(b)>(c)。
正确答案是:4。
图中所示的等截面圆轴配有四个滑轮。
在以下四个答案中,如何合理安排它们:(a)将c轮与d轮对调;(b)将b轮与d轮对调;(c)将b轮与c轮对调;(d)将车轮B与车轮d互换,然后将车轮B与车轮C互换。
正确答案是:第1页,共4页qx(l3?2lx2?x3)5、已知简支梁的跨度为l,ei为常数,挠曲线方程为y?,则梁的下列弯矩图图中:24ei正确答案是:6、图中y、z轴为形心主惯性轴,y1、z1轴为图形形心主轴的平行轴,下列论述中:(a)截面对距形心愈远的轴惯性矩愈小;(b) Y1和Z1轴是一对主惯性轴;(c) Y1和Z轴是一对主惯性轴;(d)特殊情况下,惯性积不为零的一对轴也定义为主惯性轴。
正确答案是:y1yc(a)(b)(c)(d)z1z7同一根简支梁在图示两种状态下的变形分别如图示,则状态2下b 截面的挠度为().(a)7mm;(b)6mm;(c)5mm;(d)2mm.AA10KNC5KNBAC1KNB0。
一、单项选择题(每题只有一个正确答案。
每小题3分,共30分)。
1. 低碳钢试件拉伸时,关于其横截面上应力公式NF Aσ=的以下结论,正确的是……………………………………………………………………………【 】。
A. 只适用于σ≤σp ;B. 只适用于σ≤σe ;C. 只适用于σ≤σy ;D. 在试件拉断前都适用。
2.在下列四种工程材料中,不可应用各向同性假设的是………………【 】。
A .铸铁 B. 玻璃 C. 松木 D. 碳素钢3.材料的延伸率公式1100%L LLδ-=⨯中的1L 指的是……………………【 】。
A .试件断裂前的工作段长度; B. 试件屈服后的工作段长度; C. 把拉断以后的试件拼合在一起量出的工作段长度; D. 以上说法都不正确。
4.图中y 、z 为形心主惯性轴,y 1、z 1轴为图形形心主轴的平行轴,下列论述中正确的是…………………………………………【 】。
A .截面对距形心愈远的轴,其惯性矩愈小;B. y 和z 1轴为一对主惯性轴;C. y 1和z 1轴为一对主惯性轴;D. 特殊情况下,惯性积不为零的一对轴也定义为主惯性轴。
题一(4)图 5.如果梁上某段承受三角形分布荷载,那么该梁段的挠曲线是………………【 】。
A. 三次曲线; B. 四次曲线; C. 五次曲线; D. 六次曲线。
6.图示两相同的简支梁,在图(I )所示力F 作用下,A 截面的转角和B 点的挠度分别为,I A θ,,I B y ;在图(II )所示力偶e M 作用下,A 截面的转角和B 点的挠度分别为,II A θ,,I I B y ;当力F 与力偶e M 在数值上相等时,下列关系式中正确的是…………………………………【 】。
A. ,I ,II B B y y =;B. 数值上,I ,II A B y θ=;C. ,I ,II A A θθ=;D. 以上答案都不对。
7. 关于弹性体受力后某一方向的应力与应变,正确的论述是………………【 】。
重庆大学846材料力学一考研资料(最新资料)
一、历年真题、答案
1、材料力学1995-2001,2008,2009年9套,理论力学与材料力学2003-2005年3套,材料力学与结构力学2005-2007共3套,历年真题主要用来研究考研的考点,重点和出题思路,为考研必备参考资料,复印版。
68.00
2、真题答案:材料力学1995-2001年7套,为标准答案,材料力学与结构力学:2003-2007共5套材料力学部分的手写版参考答案,本校本专业优秀研究生整理,有利于考生检验复习效果,分析解题思路,把握得分点和解题步骤,手写复印版。
78.0
0全部真题128.00注:本部分不单独出售某一年份真题。
二、考研核心笔记、授课讲义
1、材料力学讲义以及教学大纲(杨昌棋教授),为本校本专业老师上课时所用讲义,因讲课老师参与出题,帮助考生了解出题思路和出题动向。
121页,打印版。
78.00
2、材料力学课程与材料力学课程实验教学大纲,主要列出材料力学的重点难点,有利于考生有针对性地进行复习,为考生节省大量的宝贵时间。
11页,打印版。
订购全套赠送此项
三、考研习题总汇
1、材料力学习题及解答,按章整理的习题,包含作图题和计算题。
为本校本专业本科生所用习题库,因授课老师即为出题老师,所以参考价值很大。
主要用来帮助考生巩固复习知识,检验复习效果。
155页,复印版。
98.00
四、辅导班笔记
1、材料力学2008年辅导班笔记,最后一届官方举办辅导班,涉及到了很多的考点和重点,具有非常高的参考价值。
23页,手写复印版。
40.00
※全部资料258.00。
重庆大学材料力学答案2.9 题图2.9所示中段开槽的杆件,两端受轴向载荷P 的作用,试计算截面1-1和2-2上的应力。
已知:P = 140kN ,b = 200mm ,b 0 = 100mm ,t = 4mm 。
题图2.9解:(1) 计算杆的轴力 kN 14021===P N N (2) 计算横截面的面积21mm 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注:本题的目的是说明在一段轴力相同的杆件内,横截面面积小的截面为该段的危险截面)2.10 横截面面积A=2cm 2的杆受轴向拉伸,力P=10kN ,求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ,并问m ax τ发生在哪一个截面?解:(1) 计算杆的轴力kN 10==P N (2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ (3) 计算斜截面上的应力MPa 5.37235030cos 2230=⎪⎪⎭⎫⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生的截面∵ 0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此:22πα=, 454==πα故:m ax τ发生在其法线与轴向成45°的截面上。
(注:本题的结果告诉我们,如果拉压杆处横截面的正应力,就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°的截面上,最大正应力发生在横截面上,横截面上剪应力为零)2.17 题图2.17所示阶梯直杆AC ,P =10kN ,l 1=l 2=400mm ,A 1=2A 2=100mm 2,E =200GPa 。
试计算杆AC 的轴向变形Δl 。
题图2.17解:(1) 计算直杆各段的轴力及画轴力图kN 101==P N (拉) kN 102-=-=P N (压)(2) 计算直杆各段的轴向变形mm 2.010010002004001000101111=⨯⨯⨯⨯==∆EA l N l (伸长) mm 4.05010002004001000102222-=⨯⨯⨯⨯-==∆EA l N l (缩短) (3) 直杆AC 的轴向变形m m 2.021-=∆+∆=∆l l l (缩短)(注:本题的结果告诉我们,直杆总的轴向变形等于各段轴向变形的代数和)2.20 题图2.20所示结构,各杆抗拉(压)刚度EA 相同,试求节点A 的水平和垂直位移。
( a) (b)题图2.20(a) 解:(1) 计算各杆的轴力以A 点为研究对象,如右图所示,由平衡方程可得0=∑X ,P N =2( 拉 ) 0=∑Y ,01=N(2) 计算各杆的变形01=∆lEAPl EA Pl EA l N l 245cos /222===∆(3) 计算A 点位移以切线代弧线,A 点的位移为:EA Pll x A 245cos 2=∆=∆0=∆A y (b) 解:(1) 计算各杆的轴力以A 点为研究对象,如右图所示,由平衡方程可得0=∑X ,P N 21= ( 拉 ) 0=∑Y ,P N-=2( 压 )(2) 计算各杆的变形EAPaEA a P EAl N l 222111=⨯==∆ ( 伸长 )EAPaEA a P EA l N l =⨯==∆222 ( 缩短 ) (3) 计算A 点位移以切线代弧线,A 点的位移为:EA PaEA Pa EA Pa l l A C AB x A )122(2245cos 21+=+=∆+∆='+=∆EAPal y A -=∆-=∆2 [注:①本题计算是基于小变形假设(材料力学的理论和方法都是基于这个假设),在此假设下,所有杆件的力和变形都是沿未变形的方向。
②计算位移的关键是以切线代弧线。
)2.15 如题图2.15所示桁架,α =30°,在A 点受载荷P = 350kN ,杆AB 由两根槽钢构成,杆AC 由一根工字钢构成,设钢的许用拉应力MPa 160][=t σ,许用压应力MPa 100][=c σ。
试为两根杆选择型钢号码。
题图2.15解:(1) 计算杆的轴力以A 点为研究对象,如上图所示,由平衡方程可得0=∑X ,0cos cos 12=-ααN N0=∑Y ,0sin sin 21=-+P N Nαα∴ kN 3501==P N (拉) kN 35012==N N (压) (2) 计算横截面的面积 根据强度条件:][max σσ≤=AN,有 211mm 5.21871601000350][2=⨯=≥t N A σ,21m m 75.1093≥A222mm 35001001000350][=⨯=≥c N A σ(3) 选择型钢通过查表,杆AB 为No.10槽钢,杆BC 为No.20a 工字钢。
(注:本题说明,对于某些材料,也许它的拉、压许用应力是不同的,需要根据杆的拉、压状态,使用相应得许用应力)2.25 题图2.25所示结构,AB 为刚体,载荷P 可在其上任意移动。
试求使CD 杆重量最轻时,夹角α应取何值?题图2.25解:(1) 计算杆的轴力载荷P 在B 点时为最危险工况,如下图所示。
以刚性杆AB 为研究对象0=∑AM, 02sin =⋅-⋅l P l N CD ααsin 2P N CD =(2) 计算杆CD 横截面的面积设杆CD 的许用应力为][σ,由强度条件,有ασσσsin ][2][][PN N A CD ===(3) 计算夹角α设杆CD 的密度为ρ,则它的重量为ασραασραρρρ2cos ][cos sin ][2cos PlPl l A CD A V W ==⋅=⋅== 从上式可知,当 45=α时,杆CD 的重量W 最小。
(注:本题需要注意的是:①载荷P 在AB 上可以任意移动,取最危险的工作状况(工况);② 杆的重量最轻,即体积最小。
)2.34 题图2.34所示结构,AB 为刚性梁,1杆横截面面积A 1=1cm 2,2杆A 2=2cm 2,a=1m ,两杆的长度相同,E =200GPa ,许用应力[σt ]=160MPa ,[σb ]=100MPa ,试确定许可载荷[P ]。
题图2.34解:(1) 计算杆的轴力以刚性杆AB 为研究对象,如下图所示。
0=∑AM, 03221=⋅-⋅+⋅a P a N a N即:P N N 3221=+ (1) 该问题为一次静不定,需要补充一个方程。
(2) 变形协调条件如上图所示,变形协调关系为2Δl 1 =Δl 2 (2)(3) 计算杆的变形 由胡克定理,有 111EA a N l =∆; 222EA aN l =∆ 代入式(2)得:22112EA a N EA a N =即:22112A N A N = (3) (4) 计算载荷与内力之间关系由式(1)和(3),解得:112134N A A A P +=(4) 或222164N A A A P += (5) (5) 计算许可载荷如果由许用压应力[σb ]决定许可载荷,有:])[4(31][34][34][2111211121b b b A A A A A A N A A A P σσ+=⋅+=+= )(30)(30000100)2004100(31kN N ==⨯⨯+= 如果由许用拉应力[σt ]决定许可载荷,有:])[4(61][64][64][2122212221t t t A A A A A A N A A A P σσ+=⋅+=+= )(24)(24000160)2004100(61kN N ==⨯⨯+= 比较两个许可载荷,取较小的值,即{})(24][,][m in ][kN P P P t b == (注:本题需要比较由杆1和杆2决定的许可载荷,取较小的一个值,即整个结构中,最薄弱的部位决定整个结构的许可载荷。
)2.42 题图2.42所示正方形结构,四周边用铝杆(E a =70GPa ,αa =21.6×10-6 ℃-1);对角线是钢丝(E s =70GPa ,αs =21.6×10-6 ℃-1),铝杆和钢丝的横截面面积之比为2:1。
若温度升高ΔT=45℃时,试求钢丝内的应力。
题图2.42解:(1) 利用对称条件对结构进行简化由于结构具有横向和纵向对称性,取原结构的1/4作为研究的结构如下图所示,(2) 计算各杆的轴力以A 点为研究对象,如右图所示,由平衡方程可得0=∑X ,045cos =-a s N N即: a s N N 2= ①(3) 变形协调关系如上图所示,铝杆与钢丝的变形协调关系为:a s l l ∆=∆2 ②钢丝的伸长量为:(设钢丝的截面积为A ))(22A E l N l T A E l N l T l s s s s s s s s s s +∆=+∆=∆αα ③ 铝杆的伸长量为:)2(41AE l N l T A E l N l T l a a a a a a a a a a -∆=-∆=∆αα ④ 由①②③④式,可解得:A T E E E E N s a s a sa s ⋅∆-+=)(2222αα(4) 计算钢丝的应力T E E E E A N s a sa s a s ∆-+==)(2222αασ )(3.4445)107.11106.21(1020010702210200107022663333MPa =⨯⨯-⨯⨯+⨯⨯⨯⨯⨯⨯=-- 3.8题图3.8所示夹剪,销钉B 的直径d=5mm,销钉与被剪钢丝的材料相同,剪切极限应力u τ=200Mpa ,销钉的安全系数n=4,试求在C 处能剪断多大直径的钢丝。
解:设B,C 两点受力分别为1F , 2F 。
剪切许用应力为:[]u nττ==50Mpa 对B 点,有力矩和为零可知:B M ∑=0,即:1F =4P由力平衡知:1F +P=2F∴2F =541F 其中:2F =[]τ⋅A=12.52d π故: 1F =102d π又由强度要求可知:u τ≤11F A 即: d ≤114u F πτ53.11车床的转动光杆装有安全联轴器,当超过一定载荷时,安全销即被剪断。
已知安全销的平均直径为5mm ,其剪切强度极限b τ=370Mpa ,求安全联轴器所能传递的力偶矩m.解:设安全销承受的最大力为,则:F = b τ ⨯ 214d π那么安全联轴器所能传递的力偶矩为:m = F ⋅D其中b τ=370Mpa ,b=5mm ,D=20mm ,代入数据得:力偶矩 m=145.2N m ⋅4.7求题图4.7中各个图形对形心轴z 的惯性矩z I 。