研究生误差理论试题及答案

第一章1、熟悉误差、精度、有效数字的基本概念和相关计算方法。

答案：略2、用两种方法分别测量L1=50mm，L2=80mm。

测得值各为50.004mm，80.006mm。

试评定两种方法测量精度的高低。

解：两种测量方法进行的测量绝对误差分别为：δ1＝50.004-50＝0.004（mm）；δ2＝80.006-80＝0.006（mm）；两种测量方法的相对误差分别为：δ1／L1＝0.004/50=0.008%；和δ2／L2＝0.006/80=0.0075 %；显然，测量L2尺寸的方法测量精度高些。

3、若某一量值Q用乘积ab表示，而a与b是各自具有相对误差f a和f b的被测量，试求量值Q的相对误差。

解：∵相对误差=绝对误差/真值=(测得值-真值)/真值∴ a = a0(1+f a)；b = b0(1+f b)；式中a0、b0分别为a、b的真值。

则Q =ab = a0(1+f a) b0(1+f b)≈a0 b0(1+f a+ f b)因此，Q的相对误差约为（f a+ f b)第二章1、在立式测长仪上测量某校对量具，重复测量5次，测得数据（单位为mm）为20.0015，20.0016，20.0018，20.0015，20.0011。

若测量值服从正态分布，试以99%的置信概率确定测量结果。

解：①求算术平均值②求残余误差：各次测量的残余误差依次为 0，0.0001，0.0003，0，-0.0004。

③求测量列单次测量的标准差用贝塞尔公式计算：用别捷尔斯公式计算：④求算术平均值的标准差⑤求单次测量的极限误差和算术平均值的极限误差因假设测量值服从正态分布，并且置信概率P=2Φ(t)=99%，则Φ(t)=0.495，查附录表1 正态分布积分表，得置信系数t=2.6。

故：单次测量的极限误差：算术平均值的极限误差：⑥求得测量结果为：2、甲、乙两测试者用正弦尺对一锥体的锥角α个各重复测量 5 次，测得值如下：α甲：7°2’20”，7°3’0”，7°2’35”，7°2’20”，7°2’15”，α乙：7°2’25”，7°2’25”，7°2’20”，7°2’50”，7°2’45”；试求其测量结果。

误差分析试题及答案1. 误差的定义是什么？答案：误差是指测量值与真实值之间的差异。

2. 误差的来源有哪些？答案：误差的来源包括系统误差、随机误差和疏忽误差。

3. 请简述系统误差和随机误差的区别。

答案：系统误差是指在相同条件下重复测量时，误差值保持恒定或按一定规律变化的误差；随机误差则是指在相同条件下重复测量时，误差值随机变化，没有固定规律。

4. 什么是绝对误差和相对误差？答案：绝对误差是指测量值与真实值之间的绝对差值；相对误差是指绝对误差与真实值之比。

5. 如何减小测量误差？答案：减小测量误差的方法包括：使用更精确的测量工具、改进测量方法、多次测量取平均值、使用误差补偿技术等。

6. 误差分析中常用的统计方法有哪些？答案：误差分析中常用的统计方法包括：平均值、标准偏差、方差、置信区间等。

7. 请解释误差传播的概念。

答案：误差传播是指当一个物理量由多个测量值通过某种函数关系计算得到时，各个测量值的误差如何影响最终结果的误差。

8. 误差传播的一般公式是什么？答案：误差传播的一般公式为：Δf = √((∂f/∂x1)²Δx1² + (∂f/∂x2)²Δx2² + ... + (∂f/∂xn)²Δxn²)，其中f是函数，x1, x2, ..., xn是变量，Δx1, Δx2, ..., Δxn是变量的误差。

9. 什么是误差限？答案：误差限是指测量值在一定置信水平下，真实值可能落在的区间范围。

10. 误差分析在实际工程中的意义是什么？答案：误差分析在实际工程中的意义在于：确保测量结果的准确性和可靠性，为设计、生产和质量控制提供科学依据。

误差理论和测量平差试卷及答案6套试题+答案(总23页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《误差理论与测量平差》课程自测题（1）一、正误判断。

正确“T”，错误“F”。

（30分）1．在测角中正倒镜观测是为了消除偶然误差（）。

2．在水准测量中估读尾数不准确产生的误差是系统误差（）。

3．如果随机变量X和Y服从联合正态分布，且X与Y的协方差为0，则X与Y 相互独立（）。

4．观测值与最佳估值之差为真误差（）。

5．系统误差可用平差的方法进行减弱或消除（）。

6．权一定与中误差的平方成反比（）。

7．间接平差与条件平差一定可以相互转换（）。

8．在按比例画出的误差曲线上可直接量得相应边的边长中误差（）。

9．对同一量的N次不等精度观测值的加权平均值与用条件平差所得的结果一定相同（）。

10．无论是用间接平差还是条件平差，对于特定的平差问题法方程阶数一定等于必要观测数（）。

11．对于特定的平面控制网，如果按条件平差法解算，则条件式的个数是一定的，形式是多样的（）。

12．观测值L的协因数阵Q LL的主对角线元素Q ii不一定表示观测值L i的权（）。

13．当观测值个数大于必要观测数时，该模型可被唯一地确定（）。

14．定权时σ0可任意给定，它仅起比例常数的作用（）。

15．设有两个水平角的测角中误差相等，则角度值大的那个水平角相对精度高（）。

二、用“相等”或“相同”或“不等”填空（8分）。

已知两段距离的长度及其中误差为±;23±。

则：1．这两段距离的中误差（ ）。

2．这两段距离的误差的最大限差（ ）。

3．它们的精度（ ）。

4．它们的相对精度（ ）。

三、 选择填空。

只选择一个正确答案（25分）。

1．取一长为d 的直线之丈量结果的权为1，则长为D 的直线之丈量结果的权P D =（ ）。

a) d/D b) D/dc) d 2/D 2 d) D 2/d 22.有一角度测20测回，得中误差±秒，如果要使其中误差为±秒，则还需增加的测回数N=（ ）。

误差试题及答案一、选择题1. 测量误差的来源不包括以下哪一项？A. 仪器误差B. 环境误差C. 人为误差D. 计算误差答案：D2. 绝对误差和相对误差的关系是？A. 绝对误差是相对误差的倍数B. 相对误差是绝对误差的倍数C. 两者之间没有直接关系D. 相对误差是绝对误差与测量值的比值答案：D3. 在测量中，误差的减小可以通过以下哪种方式实现？A. 增加测量次数B. 使用更精确的仪器C. 改进测量方法D. 所有以上选项答案：D二、填空题1. 误差是测量值与_________之间的差异。

答案：真值2. 误差可以分为系统误差和_________误差。

答案：随机3. 误差的表示方法有绝对误差和_________误差。

答案：相对三、简答题1. 请简述如何减小测量误差。

答案：减小测量误差可以通过以下方法实现：使用更精确的测量仪器、改进测量方法、增加测量次数以进行平均、控制环境条件以减少环境误差、对测量人员进行培训以减少人为误差。

2. 什么是系统误差？请举例说明。

答案：系统误差是指在重复测量过程中，误差值保持恒定或按照一定规律变化的误差。

例如，使用一个校准不准确的温度计测量室温，每次测量结果都会比实际温度高0.5摄氏度，这就是系统误差。

四、计算题1. 假设一个测量值的真值为100，测量值为102，计算绝对误差和相对误差。

答案：绝对误差 = 102 - 100 = 2相对误差 = (2 / 100) * 100% = 2%2. 如果一个测量值的相对误差为3%，真值为500，求测量值。

答案：测量值 = 500 * (1 + 3%) = 500 * 1.03 = 515。

《误差理论与测量平差基础》课程试卷《误差理论与测量平差基础》课程试卷答案武 汉 大 学2007年攻读硕士学位研究生入学考试试题考试科目：测量平差 科目代码： 844注意：所有的答题内容必须答在答题纸上，凡答在试题或草稿纸上的一律无效。

可使用计算器。

一、填空题（本题共40分，共8个空格，每个空格5分）1．在图1所示水准路线中，A 、B 为已知点，为求C 点高程，观测了高差1h 、2h ，其观测中误差分别为1σ、2σ。

已知1212σσ=，取单位权中误差02σσ=。

要求平差后P 点高程中误差2C mm σ≤， 则应要求1σ≤ ① 、2σ≤ ② 。

2．已知观测值向量1,13,12,1X Z Y ⎡⎤⎢⎥=⎢⎥⎣⎦的协方差阵310121013ZZD -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，12,12Y Y Y ⎡⎤=⎢⎥⎣⎦，若设权11Y P =，则权阵XX P = ③ ，YY P = ④ ，协因数阵12Y Y Q = ⑤ ，1Y X Q = ⑥ 。

3．已知平差后某待定点P 的坐标的协因数和互协因数为PX Q ˆ、PY Q ˆ和PP Y X Q ˆˆ，则当PPY X Q Q ˆˆ=，0ˆˆ<PP Y X Q 时，P 点位差的极大方向值=E ϕ ⑦ ，极小方向值=F ϕ ⑧ 。

二、问答题（本题共45分，共3小题，每小题15分）1．在图2所示三角形中，A 、B 为已知点，C 为待定点，同精度观测了1234,,,L L L L测量平差 共3页 第1页共4个方位角，1S 和2S 为边长观测值，若按条件平差法平差：（1）应列多少个条件方程；（2）试列出全部条件方程（不必线性化）。

2．在上题中，若设BAC ∠、ABC ∠和ACB ∠为 参数1X 、2X 、3X ，（1）应采用何种函数模型平差；（2）列出平差所需的全部方程（不必线性化）。

3. 对某控制网进行了两期观测。

由第一期观测值得到的法方程为111111ˆT T B PB X B PL =，由第二期观测值得到的法方程为222222ˆT T B P B X B P L =。

《误差理论与数据处理》试卷一一．某待测量约为 80m，要求测量误差不超过 3％，现有级 0－300m 和级 0－100m 的两种测微仪，问选择哪一种测微仪符合测量要求（本题 10 分）二．有三台不同的测角仪，其单次测量标准差分别为：＝′，＝′，＝′。

若每一台测角仪分别对某一被测角度各重复测量 4 次，并根据上述测得值求得被测角度的测量结果，问该测量结果的标准差为多少（本题 10 分）三．测某一温度值 15 次，测得值如下：（单位：℃）, , , , , , , , ,, , , , ,已知温度计的系统误差为℃,除此以外不再含有其它的系统误差，试判断该测量列是否含有粗大误差。

要求置信概率 P=%，求温度的测量结果。

（本题 18 分）四．已知三个量块的尺寸及标准差分别为：l mm;l mm;l mm求由这三个量块研合后的量块组的尺寸及其标准差（ 0 ）。

（本题 10 分）五．某位移传感器的位移 x与输出电压 y的一组观测值如下：（单位略）1510152025xy设 x无误差，求 y对 x的线性关系式，并进行方差分析与显著性检验。

（附：F(1，4)=，F(1，4)=，F(1，4)=）（本题 15 分）六．已知某高精度标准电池检定仪的主要不确定度分量有：①仪器示值误差不超过v，按均匀分布，其相对标准差为 25%；②电流测量的重复性，经 9 次测量，其平均值的标准差为 v;③仪器分辨率为v，按均匀分布，其相对标准差为 15% 。

求该检定仪的不确定度分量，并估计其合成标准不确定度及其自由度。

（本题 10 分）七．由下列误差方程，求 x、 y的最佳估计值及其精度(单位略)。

（本题 12 分）v 2x yv x yv4 x yv x 4 y八．简答题（3 小题共 15 分）1.在实际测量中如何减小三大类误差对测量结果的影响2.简述系统误差合成与随机误差合成的方法。

3.平稳随机过程的必要条件与各态历经随机过程的充分条件是什么其特征量的估计方法有何不同分别写出它们的特征量均值与方差的估计公式。

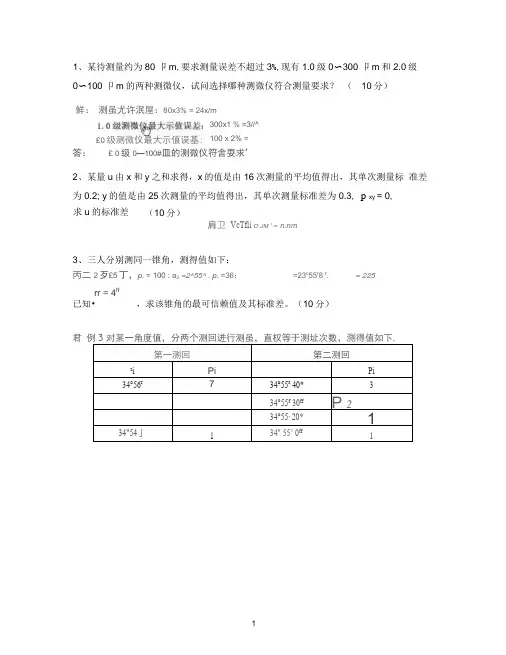
1、某待测量约为80卩m ,要求测量误差不超过3%,现有1.0级0〜300卩m 和2.0级 0〜100卩m 的两种测微仪，试问选择哪种测微仪符合测量要求？ （ 10分） 答： £ 0级0—100#皿的测微仪符舎耍求’2、某量u 由x 和y 之和求得，x 的值是由16次测量的平均值得出，其单次测量标 准差为0.2; y 的值是由25次测量的平均值得出，其单次测量标准差为0.3, p xy = 0,肩卫 VcTfli O JM ' = n.nm3、三人分别测同一锥角，测得值如下： 丙二2歹£5丁，p. = 100 : a 2 =2^55^ . p. =36； =23c 55r 8 r .= 225rr = 4ff 已知•，求该锥角的最可信赖值及其标准差。

（10分）君 例对某一角度值，分两个测回进行测虽，直权等于测址次数，測得值如下,第一测回第二测回ai PiPi34°56r734°55r 40* 334°55f 30ffP 234°55, 20*134"54」134" 55’ 0ff1300x1 % =3//^100 x 2% =求u 的标准差（10分）鮮： 测虽尤许泯屋：80x3% = 24x/m£0级测微仪最大示值误基:34°55, 70*1會34"占10”134“55」2抨対50*1解：第一测回的加权平均值及标准差2,1x 7 + K x 2 护馮=34a54F+ - Z +- - = 34°55J36ff0 17 + 1 + 2q =24；s =J96J S =—3石"工pp： =7x(24")' +1 x(-96”『+2x(_36*『= 15840x('')2第二测回的加权平均值及标准差矶_ "“口十40" x 3 + 30" x2+ 20ff x 1 + 70F x 1 +10* x I + 50ff x I晋a7= 34 54 + - -----* 3^2 + 1 + 1+1 + 1 + 1=3*5 亍33”序号 D/mmV 』艸 VtlpmI 25X ）360-04 0J6 225.0365 +0.1 0.01 3 05.0362 -0.2 0.04 4 25.0364 0 0 5 25.0367 +03 0.09 6 25X ）363 -0.1 0.01 7 25X ）366 +0,2 0,04 8251）363 -0.1 0.01 9 25.0366 +0.2 0.04 1025X ）3640 0心10 工g =250364用协 D=0工岭2 = 040/7777，4、用一标准件测某一被测量12次，测得值如下：（单位mm ）30. 0364 . 30. 0365 , 30. 0362 , 30. 0364 * 30. 0367 T 30. 036330, 0366 . 30. 0364 T 30. 03G3 , 30, 0366 . 30. 0364 T 30. 0360已知标准量的偏差为-0.005mm ,要求置信概率P=99.73%，求测量结果。

《误差理论与数据处理》试卷一一．某待测量约为80 μm,要求测量误差不超过3％，现有 1.0 级0－300μm 和2。

0 级0－100 μm 的两种测微仪，问选择哪一种测微仪符合测量要求？（本题10 分)二．有三台不同的测角仪，其单次测量标准差分别为： ⎛ 1＝0.8′, ⎛ 2＝1.0′，⎛ 3＝0.5′。

若每一台测角仪分别对某一被测角度各重复测量4 次，并根据上述测得值求得被测角度的测量结果，问该测量结果的标准差为多少？（本题10 分)三．测某一温度值15 次,测得值如下：（单位：℃）20。

53，20。

52，20.50，20。

52，20。

53，20。

53，20。

50，20.49, 20.49, 20。

51, 20.53，20。

52, 20。

49, 20.40，20.50已知温度计的系统误差为-0。

05℃,除此以外不再含有其它的系统误差，试判断该测量列是否含有粗大误差.要求置信概率P=99.73％，求温度的测量结果。

（本题18 分）四．已知三个量块的尺寸及标准差分别为：l1 ± ⎛ 1 =（10.000 ± 0。

0004）mm;l 2 ± ⎛ 2 =（1。

010 ± 0。

0003）mm；l3 ± ⎛ 3 = (1.001 ± 0.0001) mm求由这三个量块研合后的量块组的尺寸及其标准差（ 〉 ij = 0 ).（本题10 分）五．某位移传感器的位移x与输出电压y的一组观测值如下：（单位略）x y10。

105150.5262101.0521151.5775202.1031252。

6287设x无误差，求y对x的线性关系式，并进行方差分析与显著性检验.（附：F0。

10（1，4)=4.54,F0。

05(1，4）=7.71，F0.01(1，4)=21。

2）（本题15 分)六．已知某高精度标准电池检定仪的主要不确定度分量有：①仪器示值误差不超过 ± 0。

误差理论与数据处理简答题及答案基本概念题1. 误差的定义是什么？它有什么性质？为什么测量误差不可避免？答: 误差＝测得值－真值。

误差的性质有:（1）误差永远不等于零；（2）误差具有随机性；（3）误差具有不确定性；（4）误差是未知的。

由于实验方法和实验设备的不完善, 周围环境的影响, 受人们认识能力所限, 测量或实验所得数据和被测量真值之间不可避免地存在差异, 因此误差是不可避免的。

2. 什么叫真值？什么叫修正值？修正后能否得到真值？为什么？答: 真值: 在观测一个量时, 该量本身所具有的真实大小。

修正值: 为消除系统误差用代数法加到测量结果上的值, 它等于负的误差值。

修正后一般情况下难以得到真值。

因为修正值本身也有误差, 修正后只能得到较测得值更为准确的结果。

3. 测量误差有几种常见的表示方法？它们各用于何种场合？答: 绝对误差、相对误差、引用误差绝对误差——对于相同的被测量, 用绝对误差评定其测量精度的高低。

相对误差——对于不同的被测俩量以及不同的物理量, 采用相对误差来评定其测量精度的高低。

引用误差——简化和实用的仪器仪表示值的相对误差（常用在多档和连续分度的仪表中）。

4. 测量误差分哪几类？它们各有什么特点？答: 随机误差、系统误差、粗大误差随机误差: 在同一测量条件下, 多次测量同一量值时, 绝对值和符号以不可预定方式变化着的误差。

系统误差: 在同一条件下, 多次测量同一量值时, 绝对值和符号保持不变, 或在条件改变时, 按一定规律变化的误差。

粗大误差：超出在规定条件下预期的误差。

误差值较大, 明显歪曲测量结果。

5. 准确度、精密度、精确度的涵义分别是什么？它们分别反映了什么？答: 准确度: 反映测量结果中系统误差的影响程度。

精密度: 反映测量结果中随机误差的影响程度。

精确度: 反映测量结果中系统误差和随机误差综合的影响程度。

准确度反映测量结果中系统误差的影响程度。

精密度反映测量结果中随机误差的影响程度。

《误差理论与数据处理》考试题( 卷)一、填空题（每空1分，共计25分）1．误差的表示方法有 绝对误差 、 相对误差 、 引用误差 。

2．随机误差的大小，可用测量值的 标准差 来衡量，其值越小，测量值越 集中 ，测量 精密度 越高。

3．按有效数字舍入规则，将下列各数保留三位有效数字：— ；— ；— ；— ；547300— ×105 。

4．系统误差是在同一条件下，多次测量同一量值时，误差的 绝对值和符号 保持不变，或者在条件改变时，误差 按一定规律变化 。

系统误差产生的原因有（1）测量装置方面的因素、（2） 环境方面的因素 、（3） 测量方法的因素 、（4） 测量人员方面的因素 。

5．误差分配的步骤是： 按等作用原则分配误差 ； 按等可能性调整误差 ； 验算调整后的总误差 。

6．微小误差的取舍准则是 被舍去的误差必须小于或等于测量结果总标准差的1/3~1/10 。

7．测量的不确定度与自由度有密切关系，自由度愈大，不确定度愈 小 ，测量结果的可信赖程度愈 高 。

8．某一单次测量列的极限误差lim 0.06mm σ=±，若置信系数为3，则该次测量的标准差σ= 0.02mm 。

9．对某一几何量进行了两组不等精度测量，已知10.05x mm σ=，20.04x mm σ=，则测量结果中各组的权之比为 16:25 。

10．对某次测量来说，其算术平均值为，合成标准不确定度为，若要求不确定度保留两位有效数字，则测量结果可表示为 (15) 。

二、是非题（每小题1分，共计10分）1．标准量具不存在误差。

（ × ） 2．在测量结果中，小数点的位数越多测量精度越高。

（ × ） 3．测量结果的最佳估计值常用算术平均值表示。

（ √ ） 4．极限误差就是指在测量中，所有的测量列中的任一误差值都不会超过此极限误差。

（ × ） 5．系统误差可以通过增加测量次数而减小。

《误差理论与测量平差基础》期末考试试题A(参考答案)一、名词解释（每题2分，共10分）1、偶然误差——在相同的观测条件系作一系列的观测，如果误差在大小和符号上都表现出偶然性。

即从单个误差看，该误差的大小和符号没有规律性，但就大量误差的总体而言，具有一定的统计规律。

这种误差称为偶然误差。

2、函数模型线性化——在各种平差模型中，所列出的条件方程或观测方程，有的是线性形式，有的是非线性形式。

在进行平差计算时，必须首先把非线性形式的函数方程按台劳公式展开，取至一次项，转换成线性方程。

这一转换过程，称之为函数模型的线性化。

3、点位误差椭圆——以点位差的极大值方向为横轴轴方向，以位差的极值分别为椭圆的长、短半轴，这样形成的一条椭圆曲线，即为点位误差椭圆。

4、协方差传播律——用来阐述观测值的函数的中误差与观测值的中误差之间的运算规律的数学公式。

如，若观测向量的协方差阵为，则按协方差传播律，应有。

5、权——表示各观测值方差之间比例关系的数字特征，。

二、判断正误（只判断）（每题1分，共10分）参考答案：X √X √X X X √√X三、选择题（每题3分，共15分）参考答案：CCDCC四．填空题（每空3分，共15分）参考答案：1. 6个2. 13个3.1/n4. 0.45. ,其中五、问答题（每题4分，共12分）1. 几何模型的必要元素与什么有关？必要元素数就是必要观测数吗？为什么？答：⑴几何模型的必要元素与决定该模型的内在几何规律有关；（1分） ⑵必要元素数就是必要观测数；（1分）⑶几何模型的内在规律决定了要确定该模型，所必须具备的几何要素，称为必要元素，必要元素的个数，称为必要元素数。

实际工程中为了确定该几何模型，所必须观测的要素个数，称为必要观测数，X F E 、0K KL Z +=LL D T LL ZZ K KD D =220ii P σσ=0)()()()(4320020=''+∆+∆+-''+-''-W y SX X x SY Y C ACA C C ACA C ρρABAC AC X X Y Y W αββ-++--=''4300arctan其类型是由必要元素所决定的，其数量，必须等于必要元素的个数。

为边长观测值，若按条件图27BC α654321D CBA 武汉大学 测绘学院误差理论与测量平差基础 课程试卷（A 卷）出题者：黄加纳 审核人：邱卫宁一.已知观测值向量的协方差阵为，又知协因数，试求观测值的权阵及观测值的权和。

（10分）二.在相同观测条件下观测A 、B 两个角度，设对观测4测回的权为1，则对观测9个测回的权为多少？（10分）三.在图一所示测角网中，A 、B 为已知点，为已知方位角，C 、D 为待定点，为同精度独立观测值。

若按条件平差法对该网进行平差：(1).共有多少个条件方程？各类条件方程各有多少个？(2).试列出全部条件方程（非线性条件方程要求线性化）。

（15分）图一四.某平差问题有以下函数模型21L ⎥⎦⎤⎢⎣⎡--=3112LL D 5112-=Q LL P 1L P 2L P A ∠B ∠BC α721,,,L L L )(I Q =⎪⎪⎩⎪⎪⎨⎧=-=--=+-+=--0ˆ03060515443121x v v v v v v v v57624312P 2(1.732,3.000P 1(1.732,1.000A(0,0)B(0,2)Ah 5h 4h 1h 3h 2C DB 试问：(1).以上函数模型为何种平差方法的模型？(2).本题中， ， ， ， ， ， 。

(10分)五.在图二所示测角网中，已知A 、B 两点的坐标和P 1、P 2两待定点的近似坐标值（见图二，以“km ”为单位），以及，，，，为同精度观测值，其中。

若按坐标平差法对该网进行平差，试列出观测角的误差方程(设，、图二 以dm 为单位)。

(10分)六.有水准网如图三所示，网中A 、B 为已知点，C 、D 为待定点，为高差观测值，设各线路等长。

已知平差后算得，试求平差后C 、D两点间高差的权及中误差。

（10分）=n =t =r =c =u =s 0000330001'''=BP α000030002'''=BP αkm S BP 0.201=km S BP 0.202=721,,,L L L 65955906'''=L 6L 5102⨯=ρxˆyˆ51~h h )(482mm V V T =5ˆhABP 2h 5h 4h 1h 3h 2P 17654321PCBA图三七.在间接平差中，参数与平差值是否相关？试证明之。

误差理论考试试题work Information Technology Company.2020YEAR一、选择题：（每小题3分，共15分）1、测量次数的增加，随机误差的算术平均值趋向于零，这称为误差的性。

A．单峰性 B. 相关性 C. 抵偿性 D. 对称性2、单位权化的实质是使任何一个变量乘以，得到的新变量权数为1。

A．测量次数 B.变量自身对应的权的平方根C. 变量自身对应的权D.单位权3、标准差是反映测量数据的。

A．分布范围 B. 分布规律C. 互相抵偿的能力D. 分散的疏密程度4、剔除粗大误差的原则中用能够迅速作出判断。

A．格罗布斯准则 B. 莱以特准则C．罗曼诺夫斯基准则 D. 狄克逊准则5、等精度测量数据的最小二乘法原理是基于原则而推导出的。

A．残差的平方和为最小 B. 算术平均值原理C．残差的和趋向于零 D. 正态分布的随机误差的性质二、填空题：（每个小题3分，共15分）1、量限为300V的电压表在100V出现最大示值误差为1.2V，则这个电压表的准确度等级S为级。

2、正确写出结果：4.319+1.38-0.453=3、按照有效数字的书写规则，数据6.08cm的误差在 cm以内。

4、在相对误差和绝对误差中，误差更适合于用来衡量测量的效果好坏。

5、不等精度测量中，可靠程度愈高的数据其相应权的值愈（大/小）三、计算题：（共70分）1、某一角度进行六组不等精度测量，各组测量结果如下：测12次得α1=60°30′26″，测20次得α2=60°30′12″， 测24次得α3=60°30′08″，测20次得α4=60°30′14″ 测28次得α5=60°30′36″，测40次得α6=60°30′18″， 求加权平均值及加权平均值标准差。

（10分） 2、已知不等精度测量方程分别为13l x y=-，24l x y=+，32l x y=-，测量数据1 5.8l =，14p =；28.4l =，26p =；30.6l =，32p =，试求最小二乘法处理的x 、y 的值是多少（ 3、15分） 4、3、某一量等精度测量了16次，得到下面的数据，20.60, 20.57, 20.56, 20.6220.61, 20.58, 20.57, 20.96, 20.61, 20.59, 20.60, 20.58, 20.57, 20.61, 20.57, 20.56 若都已经消除了系统误差。

《误差理论与测量平差》课程自测题（1）一、正误判断。

正确“T”，错误“F”。

（30分）1．在测角中正倒镜观测是为了消除偶然误差（）。

2．在水准测量中估读尾数不准确产生的误差是系统误差（）。

3．如果随机变量X和Y服从联合正态分布，且X与Y的协方差为0，则X与Y相互独立（）。

4．观测值与最佳估值之差为真误差（）。

5．系统误差可用平差的方法进行减弱或消除（）。

6．权一定与中误差的平方成反比（）。

7．间接平差与条件平差一定可以相互转换（）。

8．在按比例画出的误差曲线上可直接量得相应边的边长中误差（）。

9．对同一量的N次不等精度观测值的加权平均值与用条件平差所得的结果一定相同（）。

10．无论是用间接平差还是条件平差，对于特定的平差问题法方程阶数一定等于必要观测数（）。

11．对于特定的平面控制网，如果按条件平差法解算，则条件式的个数是一定的，形式是多样的（）。

12．观测值L的协因数阵Q LL的主对角线元素Q ii不一定表示观测值L i的权（）。

13．当观测值个数大于必要观测数时，该模型可被唯一地确定（）。

14．定权时σ0可任意给定，它仅起比例常数的作用（）。

15．设有两个水平角的测角中误差相等，则角度值大的那个水平角相对精度高（）。

二、用“相等”或“相同”或“不等”填空（8分）。

已知两段距离的长度及其中误差为300.158m±3.5cm;600.686m±3.5cm。

则：1．这两段距离的中误差（）。

2．这两段距离的误差的最大限差（）。

3．它们的精度（）。

4．它们的相对精度（）。

三、选择填空。

只选择一个正确答案（25分）。

1．取一长为d的直线之丈量结果的权为1，则长为D的直线之丈量结果的权P D=（）。

a) d/D b) D/dc) d 2/D 2 d) D 2/d 22.有一角度测20测回，得中误差±0.42秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（ ）。

2014年3月理化检测中心培训考试试题（误差理论与数据处理）一、判断下列各题，正确的在题后括号内打 ，错的打“X”。

（每小题2分，共10分） 1 .研究误差的意义之一就是为了正确地组织实验过程，合理设计仪器或选用仪器和测量方法，以便在最经济的条件下，得到理想结果。

（V ）2 .相对误差严格地可以表示为：相对误差=（测得值-真值）/平均值（X ）3 .标准量具不存在误差。

（X ）4 .精密度反映了测量误差的大小。

（X ）5,粗大误差是随机误差和系统误差之和。

（X ）6 .系统误差就是在测量的过程中始终不变的误差。

（X ）7 .计算标准差时，贝塞尔公式和最大误差法的计算公式完全等价。

（X ）8,极限误差就是指在测量中，所有的测量列中的任一误差值都不会超过此极限误差。

（X ） 9.测量不确定度，表达了测量结果的分散性。

（V ） 1,测量相对误差越小，则测量的精度就越—高—。

2,测量精确度越高，则测量误差越小。

3 .在测量中°越大，则测量精度越低。

4 .在某一测量系统中存在着不变系统误差，为了消除此系统误差的修正值为 0.003mm 则此不变系统误差为-0.003mm _。

5 .在某一测量系统中存在着测量误差，且没有办法修正，则此误差可能是未定系统一误差或随机误差。

6.245.67+4.591弋250.26。

7.25.626X1.06/27.168,测量直径为50mmi 勺a 和直径为30mmi 勺b,a 的相对测量误差为0.021,b 的相对测量误差为0.022,则a 的测量精度较高。

9 .有a 、b 两次测量，a 测量的绝对误差是0.2mm 相对误差为0.003,b 测量的绝对误差是0.3mm 相对误差为0.002,这两个测量中精度较高的是b 测量。

10 .精确度与精密度的关系是：精确度越高，则精密度一高一_。

11 .一般不变系统误差可以在数据处理时消除，变化系统误差不能在 数据处理时消除。

误差理论试题及答案一、选择题1. 误差的来源主要包括（）。

A. 测量仪器的精度B. 测量方法C. 环境条件D. 所有以上答案：D2. 系统误差和随机误差的主要区别在于（）。

A. 系统误差是可预测的，随机误差是不可预测的B. 系统误差是不可预测的，随机误差是可预测的C. 系统误差和随机误差都是可预测的D. 系统误差和随机误差都是不可预测的答案：A3. 测量误差的估计方法不包括（）。

A. 标准差B. 均方根误差C. 绝对误差D. 误差传递答案：D二、填空题1. 测量误差可以分为________和________两种类型。

答案：系统误差；随机误差2. 误差的绝对值越小，表示测量结果的________越高。

答案：准确性三、简答题1. 简述如何减少测量误差。

答案：减少测量误差的方法包括：使用高精度的测量仪器，改进测量方法，控制环境条件，以及采用适当的数据处理方法，如取平均值等。

2. 描述误差传播的基本原理。

答案：误差传播的基本原理是，当一个量是由多个变量通过某种函数关系计算得到时，这些变量的测量误差会通过该函数关系传播到最终结果上。

误差传播的计算可以通过误差传播公式来进行，该公式考虑了各变量误差与函数关系之间的影响。

四、计算题1. 已知测量长度的仪器误差为±0.05cm，测量时间的仪器误差为±0.02s，计算速度的测量误差。

答案：假设长度为L，时间为T，速度为V=L/T，速度的相对误差可以通过误差传播公式计算得到。

速度的误差ΔV可以通过以下公式计算：ΔV = V * sqrt((ΔL/L)^2 + (ΔT/T)^2)其中ΔL = 0.05cm，ΔT = 0.02s。

将数值代入公式计算，得到速度的测量误差。

2. 已知一组数据的平均值为50，标准差为5，求这组数据的相对误差。

答案：相对误差可以通过以下公式计算：相对误差 = (标准差 / 平均值) * 100%将数值代入公式计算，得到相对误差的百分比。

《误差理论与数据处理》一、填空题（每空1分，共20分）1．测量误差按性质分为 _____误差、_____误差和_____误差，相应的处理手段为_____、_____和_____。

答案：系统，粗大，随机，消除或减小，剔除，统计的手段2．随机误差的统计特性为 ________、________、________和________。

答案：对称性、单峰性、有界性、抵偿性3. 用测角仪测得某矩形的四个角内角和为360°00′04″，则测量的绝对误差为________，相对误差________。

答案：04″，3.1*10-54．在实际测量中通常以被测量的、、作为约定真值。

答案：高一等级精度的标准给出值、最佳估计值、参考值5．测量结果的重复性条件包括：、、、、。

测量人员，测量仪器、测量方法、测量材料、测量环境6. 一个标称值为5g的砝码，经高一等标准砝码检定，知其误差为0.1mg，问该砝码的实际质量是________。

5g-0.1mg7．置信度是表征测量数据或结果可信赖程度的一个参数，可用_________和_________来表示。

标准差极限误差8．指针式仪表的准确度等级是根据_______误差划分的。

引用9．对某电阻进行无系差等精度重复测量，所得测量列的平均值为100.2Ω,标准偏差为0.2Ω，测量次数15次，则平均值的标准差为_______Ω，当置信因子K ＝3时，测量结果的置信区间为_______________。

0.2/sqrt(15),3*0.2/sqrt(15)10．在等精度重复测量中，测量列的最佳可信赖值是_________ 。

平均值11．替代法的作用是_________，特点是_________。

消除恒定系统误差，不改变测量条件12.对某电压做无系统误差等精度独立测量，测量值服从正态分布。

已知被测电压的真值U 0 ＝79.83 V ，标准差σ（U ）＝ 0.02V ，按99%（置信因子 k = 2.58）可能性估计测量值出现的范围： ___________________________________。