当前位置：文档之家 › 12 测量误差理论1-3传感器基本特性yanPPT课件

12 测量误差理论1-3传感器基本特性yanPPT课件

  • 格式：ppt
  • 大小：4.32 MB
  • 文档页数：53

下载文档原格式

  / 53

合集下载

传感器与检测技术ppt课件第一章

传感器与检测技术ppt课件第一章

2024/2/29
16
1.2检测技术理论基础
1.2.2 测量方法
1) 直接测量、间接测量和组合测量 (又称联立 测量)。经过求解联立方程组，才能得到被测物理量的最后
结果，则称这样的测量为组合测量。
2) 偏差式测量、零位式测量与微差式测量
3) 等精度测量与非等精度测量
4) 静态测量与动态测量
2024/2/29
2024/2/29
23
2024/2/29
3
1.1.3 传感器基本特性
当传感器的输入信号是常量，不随时间变化时，其 输入输出关系特性称为静态特性。
传感器的基本特性是指系统的输入与输出关系特性 ，即传感器系统的输出信号y(t)和输入信号（被测 量）x(t)之间的关系，传感器系统示意图如下图所 示。
2024/2/29
4
1.1.3 传感器基本特性
2．传感器的分类
（1）按照其工作原理，传感器可分为电参数式(如电阻式、 电感式和电容式)传感器、压电式传感器、光电式传感器及 热电式传感器等。
（2）按照其被测量对象，传感器可分为力、位移、速度、 加速度传感器等。常见的被测物理量有机械量、声、磁、温 度和光等。
（3）按照其结构，传感器可分为结构型、物性型和复合型 传感器。物性型传感器是依靠敏感元件材料本身物理性质的 变化来实现信号变换，如：水银温度计。结构型传感器是依 靠传感器结构参数的变化实现信号变换，如：电容式传感器。
敏感元件输出的物理量转换成适于传输或测量电信号 的元件。
测量电路(measuring circuit)： 将转换
元件输出的电信号进行进一步转换和处理的部分，如 放大、滤波、线性化、补偿等，以获得更好的品质特 性，便于后续电路实现显示、记录、处理及控制等功 能。

测量误差理论课件

测量误差理论课件
测量误差理论课件
目录 CONTENT
• 测量误差理论概述 • 系统误差 • 随机误差 • 过失误差 • 测量不确定度
01
测量误差理论概述
定义与分类
定义
测量误差是指测量结果与被测量 真值之间的差异。
分类
系统误差、随机误差和粗大误差 。
误差来源与影响
误差来源
仪器误差、观测误差、环境误差和理 论误差等。
随机误差的估计与处理
02
通过多次测量求平均值 ，减小随机误差的影响 。
03
采用合适的统计方法对 随机误差进行估计和检 验，如最小二乘法、贝 叶斯推断等。
04
在数据处理中，对随机 误差进行修正和补偿， 以提高测量结果的准确 性和可靠性。
04
过失误差
过失误差的来源与识别
03
随机误差
随机误差 随机误差的来源
环境因素
人为误差
如温度、湿度、气压等环境条件的变 化。
操作人员的主观判断、视觉误差或疲 劳等因素。
仪器误差
测量设备的老化、磨损或制造上的缺 陷。
随机误差 随机误差的来源
随机误差的特性与分布
随机误差具有随机性，即无法预测误差的具体值。
随机误差通常服从正态分布，即大多数误差值集中在平均值附近，极端误差出现的 概率较小。
系统误差的估计与处理
通过统计分析法
对大量测量数据进行统计分析，找出 系统误差的规律和大小。
通过经验估计法
根据经验，对系统误差的大小进行估 计。
通过对比验证法
通过对比不同测量方法或不同测量器 具的测量结果，验证系统误差的大小 和处理方法的正确性。
通过专家评审法
邀请专家对测量结果进行评审，找出 系统误差的来源和处理方法。

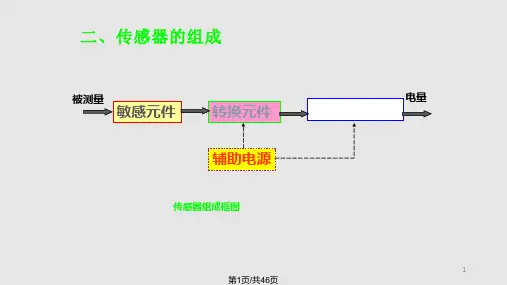
传感器及基本特性PPT课件

传感器及基本特性PPT课件
➢ 温度漂移通常用传感器工作环境温度偏离标准环 境温度（一般为20℃）时的输出值的变化量与温度变
化量之比(ξ)来表示， 即
yt y20
t
29
第29页/共46页
可靠性 ：
可靠性是反映检测系统在规定的条件 下，在规定的时间内是否耐用的一种综合 性的质量指标。
浴盆 曲线
30
第30页/共46页
稳定性：
34
第34页/共46页
一、动态参数测试的特殊性
T/℃ 动态误差
T1
T0
测试曲线
o
0
/s
图3.6 热电偶测温过程的动态特性
热电偶测温过程的动态特性
35
第35页/共46页
二、传感器的动态模型
1、微分方程 传感器的种类和形式很多，但它们的动态特性一
般都可以用下述的微分方程来描述：
an
dny dt n
n2
y(t)
n2kx(t)
根据二阶微分方程特征方程根的性质不同， 二阶系统又可分为： ① 二阶惯性系统：其特点是特征方程的根为两个负实根，
它相当于两个一阶系统串联。 ② 二阶振荡系统：其特点是特征方程的根为一对带负实部
的共轭复根。
39
第39页/共46页
2、传递函数
动态特性的传递函数在线性或线性化定常系统中是 指初始条件为0时，系统输出量的拉氏变换与输入量的拉 氏变换之比。当传感器的数学模型初值为0时，对其进行 拉氏变换，即可得出系统的传递函数
静态灵敏度则说明其静态特性。用方程式描述其动态特性的传
感器就称为一阶系统，一阶系统又称为惯性系统。
38
第38页/共46页
3） 二阶系统
二阶系统的微分方程为
a2

第二章-、传感器的基本特性PPT课件

第二章-、传感器的基本特性PPT课件
➢ 一个起始静止的二阶系统,输入正弦信号,频 率为ω时输出拉氏变换为：
传感器的非线性误差通常用相对误传差感表器示实：际特性曲
线与拟合直线之间
L
Lmax Y
100%
FS
的最大偏差 Y
Y=kx+b
线性度 Yi
传感器满量程输出
Lmax X
Xi
6
7
直线拟合线性化
▪ 出发点： 获得最小的非线性误差
拟合方法： ①理论拟合； ②过零旋转拟合； ③端点连线拟合； ④端点连线平移拟合； ⑤最小二乘拟合；
a nd d n tn y a 1d d y x a 0 y b m d d tm m x b 1d d x t b 0 x
式中： Y—输出；X—输入；ai 、bi为常数
35
t0 y0 时
y(s)=L[F(t)]=0 y(t)estdt x(s)=L[x(t)]=0 x(t)estdt
两边取拉氏变换，将实函数变换到复变函数
t
y(t)=1-e-
(2 - 10)
相应的响应曲线如图 2 - 7 所示。 由图可见, 传感器存在 惯性, 它的输出不能立即复现输入信号, 而是从零开始, 按指数 规律上升, 最终达到稳态值。理论上传感器的响应只在t趋于无 穷大时才达到稳态值, 但实际上当t=4τ时其输出达到稳态值的 98.2%, 可以认为已达到稳态。τ越小, 响应曲线越接近于输入 阶跃曲线, 因此, τ值是一阶传感器重要的性能参数。
ΔLmax x
11
返回
上一页
下一页
④端点连线平移拟合
▪ 在端点连线拟合基础上使直线平移，移动距离 为原先的一半 L2L1L3LMax y ΔLmax
ΔL1 x

传感器 第一章 传感器的一般特性PPT课件

传感器 第一章 传感器的一般特性PPT课件

第一章 传感器的一般特性 山东理工大学机械学院
二．迟滞
传感器在正(输入量增大)反（输入量减 小）行程中输出输入曲线不重合称为迟 滞。迟滞特性如图所示，它一般是由实 验方法测得。迟滞误差一般以满量程输 出的百分数表示,即
y yFS
⊿Hmax
x 0
迟滞特性
H 1 /2 H m/y a F x S 1% 00
第一章 传感器的一般特性 山东理工大学机械学院
取决于传感器本身，可通过传感器本身的改善来加 以抑制，有时也可以对外界条件加以限制。
外界影响
冲击与振动 电磁场
温度 供电
输入
传感器
输出
线性 滞后
重复性 灵敏度
各种干扰稳定性 温漂 稳定性(零漂)
分辨力
衡量传感器静态特 性的主要技术指标
误差因素 传感器输入输出作用图
①理论拟合；②过零旋转拟合；③端点连线拟合； ④端点连线平移拟合； ⑤最小二乘拟合；⑥ 最小包容拟合
第一章 传感器的一般特性 山东理工大学机械学院
a)理论拟合 c)端点连线拟合
直线拟合方法 b)过零旋转拟合 d)端点连线平移拟合
第一章 传感器的一般特性 山东理工大学机械学院最小 Nhomakorabea乘法拟合
设拟合直线方程： y=kx+b
各项系数不同，决定了特性曲线的具体形式。
静态特性曲线可实际测试获得。在获得特性曲线之后，可以说问题已经 得到解决。但是为了标定和数据处理的方便，希望得到线性关系。这时 可采用各种方法，其中也包括硬件或软件补偿，进行线性化处理。
第一章 传感器的一般特性 山东理工大学机械学院
一般来说，这些办法都比较复杂。所以在非线性误差不太大的情况下， 总是采用直线拟合的办法来线性化。

传感器基本特性PPT课件

传感器基本特性PPT课件
本章知识要点
• 传感器的定义、组成及分类。 • 传感器静态特性和动态特性的定义。 • 衡量传感器静态特性的主要指标及各指
标的含义。 • 传感器动态特性的分析方法（要求掌握
一阶的传感器动态特性）。
2.1 传感器的定义及分类
一、传感器的定义
四层含义：
（1）传感器是一种测量器件或装置； 发电机是不是传感器？
一个动态特性好的传感器，其输出将再现输入量的 变化规律，即具有相同的时间函数。实际的传感器，输 出信号将不会与输入信号具有相同的时间函数, 这种输 出与输入间的差异就是动态误差。
动态误差
输出稳定后与理想输出量的误差 输入量跃变，输出量在过渡状态的误差
举例
把 一 支 热 电 偶 从 温 热电偶
度为t0℃环境中迅速插入
1. 微分方程
微分方程 传递函数 频率响应函数
条件：线性时不变系统——常系数线性微分方程
an ddntnyan1 ddntn11ya1 ddyta0y bmddmtmxbm1 ddmtm1x1 b1 ddxtb0x
式中，a0、a1、…, an, b0、b1、…., bm是与传感器的结构特性有关的 常系数。
（一)传感器的动态响应特性
研究动态特性可以从时域和频域两个方面采用瞬态 响应法和频率响应法来分析。
输入标准信号
阶跃函数 正弦函数 指数函数
冲击函数
阶跃响应法（时域） 频率响应法（频域）
典型输入信号
• 对于阶跃信号，传感器的响应称为阶跃响应或瞬态响 应，它是指传感器在瞬变非周期信号作用下的响应特 性。这对传感器来说是一种最严峻的状态，如果传感 器能复现这种信号，那么就能很容易地复现其他种类 的输入信号，其动态性能指标也必定会令人满意。

传感器与检测技术第二讲——传感器的基本特性PPT课件

类，即将传感器分为：有 源传感器和无源传感器；
按输出信号的性质分类，即将传感器分为： 模拟式传感器和数字式传感器。数字式传感 器输出为数字量，便于与计算机联用，且抗 干扰性较强，例如：盘式角度数字传感器， 光栅传感器等。
2021/3/24
2021
13
13
2021
14
传感器的基本特性，即输入-输出特性，基本特性可用静 态特性和动态特性来描述。
n 灵敏度是传感器在稳态下输出增 量与输入增量的比值。
n 对于线性传感器，其灵敏度就是 它的静态特性的斜率，其
n
sn=y/x
2021/3/24
2021
17
17
2021/3/24
图1-6 传感器的灵敏度
2021
18
18
非线性传感器的灵敏度是一个随工作点而变的变量， 如图1-6（b）所示，其
sn=dy/dx=df(x)/dx
传感器及检测技术
第二讲传感器基本特性
2021
1
1.传感器的分类
2021/3/24
2021
2
2
一. 传感器的分类
传感器有许多分类方法，但常用的
分类方法有两种：
一种是按被测输入量来分；
另一种是按传感器的工作原理来分。
2021/3/24
2021
3
3
1) 按被测量分类 这一种方法是根据被测量的性质进行分类，
EZ=∆mMAX/YFS·100%
2021/3/24
2021
21
21
2021/3/24
图1-7 传感器的重复性
2021
22
22
5. 分辨力
传感器的分辨力是在规定测量范围内

《传感器的基本特性》课件


电磁兼容性
总结词
描述传感器在电磁环境中的性能表现 。
详细描述
传感器在电磁干扰环境下的抗干扰能 力，以及电磁屏蔽、防雷击等方面的 性能表现。
化学稳定性
总结词
描述传感器在各种化学环境中的性能表现。
详细描述
传感器在不同化学物质、腐蚀性气体、液体 等环境中的耐腐蚀、抗氧化等性能表现。
抗干扰能力
总结词
描述传感器在各种干扰下的性能表现。
详细描述
迟滞性表示传感器在正向和反向输入条件下，输出-输入曲线之间的偏差程度。迟滞性通常是由于传感器内部物 理特性的非对称性所引起的。迟滞性越小，说明传感器在正向和反向输入条件下输出-输入曲线的一致性越好。
重复性
总结词
重复性是衡量传感器在不同输入条件下输出一致性的参数。
详细描述
重复性表示在同一输入条件下，多次测量所得输出结果的一致性。重复性越好，说明传感器在不同输 入条件下输出的稳定性越好。重复性是衡量传感器性能的重要参数之一，对于需要高精度测量的应用 尤为重要。
传感器通常由敏感元件和转换元件组成，有时还包括转换电 路。敏感元件是指传感器中能直接感受或响应被测量的部分 ；转换元件是指传感器中能将敏感元件感受或响应的被测量 转换成适于传输或测量的电信号部分。
传感器的分类
按输入量
物理量传感器、化学量 传感器、生物量传感器
。
按工作原理
结构型传感器、物性型 传感器、复合型传感器
智能化
总结词
智能化传感器具有自动校准、自动补偿、自动识别等 功能，能够自适应环境变化和工作条件变化。智能化 传感器可以实现更高的测量精度和可靠性。
详细描述
智能化传感器是指具有自动校准、自动补偿、自动识 别等功能的传感器。智能化传感器能够自适应环境变 化和工作条件变化，提高测量精度和可靠性。例如， 智能化温度传感器可以通过自动校准和补偿技术，消 除环境温度和电路参数变化对测量结果的影响，实现 高精度温度测量。同时，智能化传感器还可以通过自 动识别技术，对不同目标进行快速准确的识别和分类 。

《传感器与检测技术》课件PPT 1 传感器的一般特性-精品文档


(a) 线性传感器
(b) 非线性传感器
3、迟滞

正（输入量增大）反（输入量减小）行 程中输出输入曲线不重合称为迟滞
H m a x ( ) 1 0 0 % H y F S
H max —正反行程间输出的最大差值。
Y
H max
x
产生这种现象的主要原因是由于传感器敏感元件材料的 物理性质和机械另部件的缺陷所造成的，例如弹性敏感元件 弹性滞后、运动部件摩擦、传动机构的间隙、紧固件松动等。 迟滞误差又称为回差或变差。
传感器的线性度是指在全量程范围内校准曲线与拟合直线
之间的最大偏差值Δ x ymax 与满量程输出值 yFS 之比。线性度也称
为非线性误差，用

L
表示，即
y
y a x L m 1 0 0 % y m a x 校准曲线 y FS
拟合直线
y m ax
式中： Δymax——最大非线性绝对误差； yFS——满量程输出值。
2
1.1 传感器的静态特性
传感器的静态特性是指被测量的值处于稳定状态时 的输出与输入的关系。如果被测量是一个不随时间变化， 或随时间变化缓慢的量，可以只考虑其静态特性， 这时 传感器的输入量与输出量之间在数值上一般具有一定的对
应关系，关系式中不含有时间变量。对静态特性而言，传
感器的输入量x与输出量y之间的关系通常可用一个如下的 多项式表示：
yF
S
x m ax x
直线拟合线性化

出发点
拟理论拟合； ②过零旋转拟合； ③端点连线拟合； ④端点连线平移拟合； ⑤最小二乘拟合； ⑥最小包容拟合
①理论拟合
拟合直线为传感器的理论特性，与实际测试值无关。 方法十分简单，但一般说

《测量误差理论》课件


系统误差
随机误差
粗大误差
02 系统误差
系统误差的特点
确定性
系统误差是确定的，可以通过数学模型或公 式表示。
可预测性
系统误差可以通过一定的方法进行预测或估 算。
重复性
在相同条件下，系统误差会重复出现。
周期性
某些系统误差呈现周期性变化。
系统误差的来源
仪器缺陷
测量仪器本身存在的缺陷或误差，如 刻度不准确、零点偏移等。
非系统性
过失误差通常是由于测量过程中的失误或疏忽造成的，因此它不 具备系统性，不会按照一定的规律影响测量结果。
不可预测性
由于过失误差是由于人为因素引起的，通常难以提前预测或估计其 大小。
随机性
过失误差的大小和方向通常都是随机的，没有固定的模式或趋势。
过失误差的来源
操作失误
测量过程中的操作失误，如读错刻度、按下 错误的按钮等。
不确定度的来源
随机效应和系统效应。随 机效应导致随机测量不确 定度，而系统效应导致系 统测量不确定度。
测量不确定度的评估方法
直接测量法
通过直接观测和数据处理计 算测量不确定度。
1
间接测量法
通过观测多个量来计算总不 确定度，并考虑各量之间的
相互影响。
蒙特卡洛模拟法
通过随机抽样方法模拟观测 数据的分布，并计算测量不 确定度。
定期校准仪器
确保测量仪器的准确性和可靠性，及时修复 故障。
实施复核制度
对测量结果进行复核，检查是否有记录错误 ，并进行修正。
05 测量不确定度
测量不确定度的定义
01
02
03
测量不确定度
表示测量结果的可信程度 或可靠性的参数了测量结果的不确 定性，即测量结果的不肯 定程度。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（三）系统误差的抵消与修正 (1) 测量前尽可能消除导致系统误差的来源; (2) 建立误差模型,修正系统误差; 修正值：用代数法与未修正测量结果相加,以补
偿其系统误差的值。
Cxxcontrue
(3) 在测量过程中采用合适的测量方法,使系统误 差被抵消而不带到测量结果中。
a) 定值系统误差的抵消方法 ➢ 替代法
dB 2l0 g A A A2l0 g 1( A A ) dB
增益的绝对
dB 2l0g1 (A) dB 误差
增益的相对 误差
2 测量误差的性质与基本规律
一. 测量误差的来源 1. 测量仪器（装置） ➢ 标准量具误差 ➢ 仪器误差 ➢ 附件误差 2. 环境条件 3. 测量方法 4. 人为因素
二. 误差分类
表示形式
误差
性质特点
绝对 误差
相对 误差
系统 误差
随机 粗大 误差 误差
系统误差
（一）产生系统误差的影响因素
系统误差是由固定不变的或按确定规律变化的因素 造成，在条件充分的情况下这些因素是可以掌握的。
（二）系统误差的基本规律 定值系统误差
变值系统误差
➢累积系统误差 ➢周期性系统误差 ➢按复杂规律变化的系 统误差
1、绝对误差：
绝对误差 ＝ 测得值－ 真值
exxtrue
被测量的真值， 常用约定真值 代替
exxcontrue
2、相对误差：绝对误差与被测量真值之比
rtr
xxtru xtrue
e10% 0
实际相对误差：
rc
xxcontrue10% 0 xcontrue
示值相对误差：
rx
xxcotnrue10% 0 x
用1.0级0~100V测量100V时，有最大绝对误差
e m a U x fC % 1 1 0 .0 % 0 1 .0 ( V ) 最大相对误差 rma xeU ma x1 1.00 100 % 0 1.0%
相对项
数字仪表误差的表示： 系数
固定项 系数
ema x (a% xb% F)R 或 ema x(a% xndi)gi量t程上限
例1-1：某电流表满量程值为10A，在进行一组电流 测量时，满量程内出现的绝对误差 e 0.03~0.04A, 此电流表的精度等级应为多少？
解：引用误差
rf e U m fa x10 % 001 .00 410 % 00.4%
由于 0.2rf 0.40.5, 因此此电流表的精度等 级应为0.5级。
lim i 1 0 n n
3. 最佳估计值及其标准偏差
1) 测量列的算术平均值
X
n
Xi
i 1 n
X 1n[a(1)(a2)(ai)(an)]
例2-1补 ∶用一个4位多量程数字频率计测量标准
频率信号源输出100kHz时的频率，量程选择
为0~10MHz，频率计测量值为101kHz，求频
率计在该点的绝对误差和相对误差。
约定真值
测得值
解：绝对误差
ex x co trnu 1 e 0 11 01 (k 0H )
相对误差
rcx xcxo cto n rtu n ru ee 10 % 01101 0%
间接测量 二. 误差
误差 ＝ 测得值－ 真值
真值：观测一个量时，该量本身所具有的真实
大小。 分类：
理论真值
三角形内角之 和恒为180º
千克原器的最 小不确定度为 0.004mg
约定真值——对于给定的目的，被赋予适当 不确定度的特定量的值。
指定值、最佳 估计值、约定 值或参考值
相对真值
千克副原器质量 的约定真值为1kg， 其复现的不确定 度为0.008mg。
检测系统的组成
第三节 测量误差分析基础
测量与测量误差的基本概念 测量误差的性质与基本规律 测量误差的传递
1 测量与测量误差的基本概念
一. 测量
——以确定量值为目的的一组操作。
被测量
Ax
因此，测量结果
x x0
标准量/ 单位
纯粹的数 字值
量具 /度量器： 基准器 标准器 工作量具
测量方法分为： 直接测量
3、引用误差：测量量具的绝对误差与其引用值
的比 值。
量限内最大绝
引用值
e
对误差
rf xf 100%
仪表准确度等级 C ：按照引用误差进行分级
仪表引用误差 rf C%
用仪表测量某一被测量时，所产生的最大绝对
误差为
emaxxf C%
最大相对误差为
与仪表量限有关
rx
emaxxf xx
C%
越接近上限越小
应用：用电桥测量电阻 ➢ 交换法（对置法、对照法）
Rx
R1 R2
R'N
Rx
R2 R1
R' 'N
Rபைடு நூலகம் R'NR''N
b) 变值系统误差的抵消方法 ➢ 等间隔对称测量法 应用:用直流电位差计测量电压 ➢ 半周期偶数测量法(半周期法)
c)其他特殊测量方法
Ex
En Rn
Rx1Rx2 2Rx2 Rx1
Ex
示值
n=1~4
与量程对应的末位数字 所代表的值
4、分贝误差
对于电压、电流量
双口网络电压增益实际值A 电压增益测量值A u
A的分 贝值
G20lgA
Au的分 贝值
Au
Uo Ui
dB Gu G
20 lg Au 20 lg A 20 lg Au
A
Gu 20lgAu
分贝误差： dB20lgAAu dB △A=Au-A
Ex1Ex2 2Ex2 Ex1
随机误差
（一）随机误差的产生原因
（二）正态分布
1. δ的概率分布密度
测量列：x1,x2,,xi,xn
1
n
δ2
n i1 i
随机误差：i xi a
概率分布密度
f ( ) 1 e222 2
2. 随机误差的基本性质
1) 单峰性
2) 有界性
3) 对称性
4) 抵偿性
n
i
例2-5补：求以引用误差定等的1.0级、测量范围为 0~100V电压表的最大绝对误差。当用该电压表测 量50V电压时，测量结果的相对误差不超过多少？
解：最大绝对误差为
e m a U x fC % 1 1 0 .0 % 0 1 ( V )
用该电压表测量50V时的相对误差最大值为
rma xeU ma x5 1 010 % 02%
例2-8补：某待测的电压约为100V，现有0.5级、 0~300V和1.0级、 0~100V两个以引用误差定等的电 压表，问用哪一个电压表测量比较好？
解：用0.5级0~300V测量100V时，有最大绝对误差
e m a U x fC % 3 0 .5 % 0 1 .5 ( V )
最大相对误差 rma xeU ma x1 1.50 100 % 0 1.5%