斜线在平面内的射影与平面所成角习题篇

【考点梳理】一、考试内容1.平面。

平面的基本性质。

平面图形直观图的画法。

2.两条直线的位置关系。

平行于同一条直线的两条直线互相平行。

对应边分别平行的角。

异面直线所成的角。

两条异面直线互相垂直的概念。

异面直线的公垂线及距离。

3.直线和平面的位置关系。

直线和平面平行的判定与性质。

直线和平面垂直的判定与性质。

点到平面的距离。

斜线在平面上的射影。

直线和平面所成的角。

三垂线定理及其逆定理。

4.两个平面的位置关系。

平面平行的判定与性质。

平行平面间的距离。

二面角及其平面角。

两个平面垂直的判定与性质。

二、考试要求1.掌握平面的基本性质，空间两条直线、直线与平面、平面与平面的位置关系（特别是平行和垂直关系）以及它们所成的角与距离的概念。

对于异面直线的距离，只要求会计算已给出公垂线时的距离。

2.能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定，进行论证和解决有关问题。

对于异面直线上两点的距离公式不要求记忆。

3.会用斜二测画法画水平放置的平面图形（特别是正三角形、正四边形、正五边形、正六边形）的直观图。

能够画出空间两条直线、两个平面、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系。

4.理解用反证法证明命题的思路，会用反证法证明一些简单的问题。

三、考点简析1.空间元素的位置关系2.平行、垂直位置关系的转化3.空间元素间的数量关系（1）角①相交直线所成的角；②异面直线所成的角——转化为相交直线所成的角；③直线与平面所成的角——斜线与斜线在平面内射影所成的角；④二面角——用二面角的平面角来度量。

（2）距离①两点之间的距离——连接两点的线段长；②点线距离——点到垂足的距离；③点面距离——点到垂足的距离；④平行线间的距离——平行线上一点到另一直线的距离；⑤异面直线间的距离——公垂线在两条异面直线间的线段长；⑥线面距离——平行线上一点到平面的距离；⑦面面距离——平面上一点到另一平面的距离；⑧球面上两点距离——球面上经过两点的大圆中的劣弧的长度。

直线和平面垂直的定义与判定和斜线、射影、直线与平面所成的角讲义考点一：直线和平面垂直的定义与判定1.直线和平面垂直定义如果直线和平面内的任意一条直线都垂直，我们就说直线与平面互相垂直，记作.直线叫平面的垂线；平面叫直线的垂面；垂线和平面的交点叫垂足.2.直线和平面垂直的判定定理判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．符号语言：特征：线线垂直线面垂直3.基本性质一条直线垂直于一个平面，那么这条直线垂直于这个平面内的所有直线.符号语言：图形语言：4.性质定理垂直于同一个平面的两条直线平行.符号语言：图形语言：5.平面与平面垂直的性质性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直.符号语言：图形语言：对应练习：1.平面外的一条直线与内的两条平行直线垂直，那么( ).A. B. C.与相交 D.与的位置关系不确定2.已知直线a、b和平面，下列推论错误的是( ).A. B.C. D.3.若直线a⊥直线b，且a⊥平面，则有( ).A. B. C. D.或4.若P是平面外一点，则下列命题正确的是( ).A.过P只能作一条直线与平面相交B.过P可作无数条直线与平面垂直C.过P只能作一条直线与平面平行D.过P可作无数条直线与平面平行5.设是直二面角，直线，直线，且a不垂直于，b不垂直于，那么( ).A.a与b可能垂直，但不能平行B.a与b可能垂直，也可能平行C.a与b不可能垂直，但可能平行D.a与b不可能平行，也不能垂直6.设、为两个不同的平面，、m为两条不同的直线，且，有如下两个命题：①若，则；②若，则届那么( ).A.①是真命题，②是假命题B.①是假命题，②是真命题C.①②都是真命题D.①②都是假命题7.关于直线m、n与平面与，有下列四个命题：①若且，则m∥n；②若且，则；③若且，则；④若且，则m∥n.其中真命题的序号是( ).A.①②B.③④C.①④D.②③8.已知直线m⊥平面，直线，给出下列四个命题，其中正确的命题是( ).①若，则；②若，则m∥n；③若m∥n，则；④若，则.A.③④B.①③C.②④D.①②9.下面四个命题：①两两相交的三条直线只可能确定一个平面；②经过平面外一点，有且仅有一个平面垂直这个平面；③平面内不共线的三点到平面的距离相等，则；④两个平面垂直，过其中一个平面内一点作它们交线的垂线，则此垂线垂直于另一个平面其中真命题的个数是( ).A.0个B.1个C.2个D.3个10.设有不同的直线a、b和不同的平面、、，给出下列三个命题：①若，，则；②若，，则；③若，则.其中正确的个数是( )A.0B.1C.2D.311．若平面α⊥平面β，平面β⊥平面γ，则()．A．α∥γB．α⊥γC．α与γ相交但不垂直D．以上都有可能12．已知直线l⊥平面α，直线m⊂α，则()．A．l⊥m B．l∥mC．l，m异面D．l，m相交而不垂直13.已知直线⊥平面，直线平面，有四个命题：①；②；③；④.其中正确的命题是__________.(把所有正确命题的序号都填上)14．若a，b表示直线，α表示平面，下列命题中正确的有________个．①a⊥α，b∥α⇒a⊥b; ②a⊥α，a⊥b⇒b∥α；③a∥α，a⊥b⇒b⊥α；④a⊥α，b⊥α⇒a∥b.15.如图所示，四边形ABCD为正方形，SA垂直于四边形ABCD所在的平面，过点A 且垂直于SC 的平面分别交SB ，SC ，SD 于点E ，F ，G . 求证：AE ⊥SB ，AG ⊥SD .考点二：斜线、射影、直线与平面所成的角一条直线和一个平面相交，但不和这个平面垂直，这条直线叫做这个平面的斜线.过斜线上斜足外的一点间平面引垂线，过垂足和斜足的直线叫做斜线在这个平面内的射影.平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角.1、正方体中,(1)求1BD 和底面ABCD 所成的角 (2)求1BD 和面11AA D D 所成的角2、正方体中,,E F 分别是11D C 和BC 中点,O 是BD 的中点1A 1B 1C 1D ABCD 1A 1B 1C 1D(1)求EF 和底面ABCD 所成的角 (2) 求EF 和侧面11BCC B 所成的角, (3)求1B O 和底面ABCD 所成的角 (4)求1B O 和侧面11BCC B 所成的角3、正方体中,,M N 分别是1AD 和BD 的中点,(1)求1AC 和上底面1111A B C D 所成的角 (2)求MN 和底面ABCD 所成的角4、空间四边形ABCD 中,AC BC ⊥, PA ⊥平面ABC ,2AC BC ==,4PA =(1)求PB 与平面PAC 所成的角 (2)求PC 和平面PAB 所成的角5、正三棱柱的各棱长相等,是D 侧面11BCC B 的中心, (1)求ＡＤ和平面11BCC B 所成角的大小 (2)求ＡＤ和平面ＡＢＣ所成的角的大小A BCD1A 1B 1C 1D MNA BCP1A 1B 1C课后练习：1、已知a，b，c是直线，α，β是平面，下列条件中，能得出直线a⊥平面α的是（）A、a⊥c,a⊥b，其中b⊂α,c⊂αB、a⊥b,b∥αC、α⊥β，a∥βD、a∥b,b⊥α2、如果直线l⊥平面α，①若直线m⊥l,则m∥α；②若m⊥α,则m∥l；③若m∥α,则m⊥l；④若m∥l,则m⊥α, 上述判断正确的是（）A、①②③B、②③④C、①③④D、②④3、直角△ABC的斜边BC在平面α内，顶点A在平面α外，则△ABC的两条直角边在平面α内的射影与斜边BC 组成的图形只能是（）A、一条线段B、一个锐角三角形C、一个钝角三角形D、一条线段或一个钝角三角形4、下列命题中正确的是（）A、过平面外一点作这个平面的垂面有且只有一个B、过直线外一点作这条直线的平行平面有且只有一个C、过直线外一点作这条直线的垂线有且只有一条D、过平面外的一条斜线作这个平面的垂面有且只有一个5、给出下列命题：①若平面α的两条斜线段PA、PB在α内的射影长相等，那么PA、PB的长度相等；②已知PO是平面α的斜线段，AO是PO在平面α内的射影，若OQ⊥OP，则必有OQ⊥OA；③与两条异面直线都平行的平面有且只有一个；④平面α内有两条直线a、b都与另一个平面β平行，则α∥β、上述命题中不正确的命题是（）A、①②③④B、①②③C、①③④D、②③④6、如果△ABC的三个顶点到平面 的距离相等且不为零，那么△ABC的( )A、三边均与 平行B、三边中至少有一边与 平行C、三边中至多有一边与 平行D、三边中至多有两边与 平行7、下列命题正确的是()A、一条直线与一个平面平行，它就和这个平面内的任意一条直线平行B、平行于同一个平面的两条直线平行C 、与两个相交平面的交线平行的直线，必平行于这两个平面D 、平面外的两条平行直线中的一条与一个平面平行，则另一条直线也与此平面平行8、下列命题正确的是 ( )(A)αα////b a b a ⇒⎭⎬⎫⊥ (B)a b b a //⇒⎭⎬⎫⊥⊥αα (C)αα//b a b a ⇒⎭⎬⎫⊥⊥ (D)αα////b b a a ⇒⎭⎬⎫⊥9、正方体中，求1AB 和平面11A B CD 所成的角答案：DBDDC BDBA BCD 1A 1B 1C 1D。

高二数学（第28讲）斜线在平面内的射影，直线与平面所成的角。

【学习内容】斜线在平面内的射影，直线与平面所成的角。

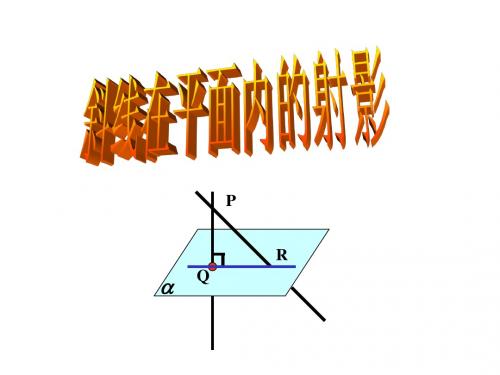
【学习指导】一、斜线在平面内的射影，斜线与平面成角问题：1．掌握斜线在平面内的射影的作法步骤：①作垂线得垂足；②连斜足与垂足得射影。

2．利用“斜线段相等 射影相等”掌握三个重要的射影：设P为△ABC所在平面外的一点，O为P在平面ABC内的射影，则有①P到△ABC的三个顶点等距离，则O为△ABC的外心。

②P到△ABC的三条边等距离（且O在△ABC的内部），则O为△ABC 的内心。

③PA⊥BC，PB⊥AC，则O为△ABC的垂心。

3．掌握线面成角的定义、范围及最小角原理。

①定义：平面的一条斜线和它在这个平面内的射影所成的锐角。

补充定义：当直线与平面垂直时，成角为90°；当直线在平面内或与平面平行时，成角为0°②范围：［0°，90°］．斜线与平面成角范围为（0°，90°）③斜线与平面成角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角。

二、三垂线定理问题1．要分清三垂线定理与逆定理：定理为“垂直射影⇒垂直斜线”；逆定理为“垂直斜线⇒垂直射影”。

2．要充分认识三垂线定理及逆定理的重要作用：①证线线垂直（将判定“空间中的两条直线是否垂直”与判定“平面中的两条直线是否垂直‘进行互相转化）；②求平面外一点到平面内一条直线的距离（常从垂足向此直线作垂线段，求出其长后再用三垂线定理及勾股定理求解）【典型例题分析】例1．如图，在正方体ABCD－A1B1C1D1中，求：（1）A1B与平面A1B1CD所成的角；（2）B1B在平面A1C1B所成角的正切值。

分析求线面成角，一定要找准斜线在平面内的射影。

（1）先找到斜足A1，再找出B在平面A1B1CD内的射影，即从B向平面A1B1CD作垂线，一定要证明它是平面A1B1CD的垂线。

这里可证BC1⊥平面A1B1CD，O为垂足，∴A1O为A1B在平面A1B1CD上的射影。

第8讲 立体几何中的最大角与最小角问题知识与方法最小角定理: 平面的斜线和它在平面内的射影所成的锐角, 是这条斜线和平面内任一直线 所成角中的最小者, 即线面角是最小的线线角. (由三余弦定理cos cos cos PAB OAB ∠θ∠=⋅ 可得）最大角定理 : 对于一个锐二面角, 在其中一个半平面内的任一条直线与另一个半平面所成 的线面角的最大值等于二面角的平面角, 即二面角是最大的线面角. (由三正弦定理sin θ= sin sin PAB α∠⋅ 可得)典型例题【例1】 设三棱锥 V ABC - 的底面是正三角形, 侧棱长均相等, P 是棱 VA 上的点 (不含端 点). 记直线 PB 与直线 AC 所成的角为 α, 直线 PB 与平面 ABC 所成的角为 β, 二面角P AC B -- 的平面角为 γ, 则（）A. ,βγαγ<<B. ,βαβγ<<C. ,βαγα<<D. ,αβγβ<<【例2】如图, 在矩形 ABCD 中, AD CD <, 现将 ACD 沿 AC 折起 至 ACD ', 使二面角A CDB -'- 的平面角为锐角, 设直线 AD ' 与 直线 BC 所成的角为 α, 直线 BD ' 与平面 ABC 所成的角为 ,AD β' 与平面 BCD ' 所成的角为 γ, 则( )A. αβγ>>B. αγβ>>C. βαγ>>D. γαβ>>【例3】 如图 (1), 在 ABC 中, 1,4AB BC B π∠===, 将 ABC 绕边 AB 翻转至ABP , 使平面 ABP ⊥ 平面 ,ABC D 是边 BC 的中点, 设 Q 是 线段 PA 上的动点, 当 PC与 DQ 所成的角取得最小值时, 线段 AQ 的长 度为 ________.图 (1)【例4】如图(1),某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ,某目标点沿墙面上的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小.若15?m,25?m,30AB AC BCM ∠===,则tan θ的最大值是________.(仰角θ为直线AP 与平面ABC 所成角)图(1)【例5】如图(1),在三棱柱111ABC A B C -中,1,,AB AC AA 两两互相垂直,1,,AB AC AA M N ==是线段11,BB CC 上的点,平面AMN 与平面ABC 所成(锐)二面角为6π.当1B M 最小时,AMB ∠=( )A.512π B.3π C.4π D.6π图(1)强化训练1.已知四棱雉 S ABCD - 的底面是正方形, 侧棱均相等, E 是线段 AB 上的点 (不含端点). 设SE 与 BC 所成的角为 1,SE θ 与平面 ABCD 所成的角为 2θ, 二面角 S AB C - 的平面角为 3θ, 则（）A. 123θθθB. 321θθθC. 132θθθD. 231θθθ2.在四面体 ABCD 中, BCD 为等边三角形, 2ADB π∠=, 二 面角 B AD C -- 的大小为α, 则 α 的取值范围是（）A. 0,6π⎛⎤⎥⎝⎦B. 0,4π⎛⎤⎥⎝⎦C. 0,3π⎛⎤⎥⎝⎦D. 0,2π⎛⎤⎥⎝⎦3.如图,在四边形ABCD 中,2,AB BC CD AD ====对角线3,BD E =是线段CD 上除端点外任一点,将ABD 沿BD 翻折成A BD ',使二面角A BD C '--的大小为120,设异面直线A D '和BE 所成的角为α,则sin α的最小值是______4.如图,已知三棱锥A BCD -的所有棱长都相等,点E 满足3DE EC =,点P 在棱AC 上运动.设EP 与平面BCD 所成的角为θ,则sin θ的最大值为_____5.如图,已知正四面体,A BCD BCD -在平面α内,点E 在线段AC 上,2,AE EC l =是平面α的垂线.在该四面体绕CD 旋转的过程中,直线BE 与l 所成的角为θ,则sin θ的最小值是( )。