UC矩阵求解

MIS资料整理一、选择1. 信息度量：信息的大小取决于信息内容消除人们认识的不确定性程度。

可以用概率来度量信息，主要用对数的相反数表示。

信息的单位为比特，是含有两个独立均等概率状态的事件所具有的不确定性能够被全部消除所需要的信息。

2. 信息的维度：信息的个人维度：时间维度指在人们需要时候及时获得信息，以及与你正在做的事情相关的信息。

空间维度阐述了信息的便利性，即人们不管在哪里，都能够获得信息。

形式维度指信息以适当的形式（声音、文本等）被提供，其次是信息的准确性。

信息的组织维度：信息流动：向上流动是信息来源于基层，通过各个管理层次向上流动。

向下流动指战略、目标和指令，向低层次流动。

信息水平流动指信息介于各职能部门和工作小组之间。

信息向外流动指向顾客、供应商、经销商或其他商业伙伴流动。

信息粒度：指信息详尽性的程度范围，粗粒度是高度概括的信息，细粒度是非常具体的信息。

3.信息系统类型：运营支持系统：事务处理系统、过程控制系统、企业协作系统。

---有效处理企业事务、控制工业过程、支持企业沟通和协作及更新数据库等。

数据需要经过加工才能为管理人员服务。

管理支持系统：管理信息系统、决策支持系统、经理信息系统。

事务处理系统：记录并处理企业事务产生的数据，可以采取批处理或者在线处理。

零售业务过程控制系统：监视和控制工业过程。

原油精炼、发电和炼钢系统。

企业协作系统：强化团队沟通。

电子邮件、视频沟通等。

管理信息系统：以预定义报告和屏幕方式提供信息，支持企业决策。

如销售分析、成本趋势报告、生产能力等。

决策支持系统：为管理人员或商务人士决策过程提供特定的交互式支持，如产品定价、收益预测等。

经理信息系统：从MIS、DSS中提取关键信息，满足主管的信息需要。

如企业绩效分析系统、竞争对手行为分析系统、支持企业战略规划的经济发展分析系统。

信息系统其他类型:专家系统：基于知识的系统，充当专家顾问，为用户提供专家建议，如诊断保养系统。

电⼦政务复习资料1、电⼦政务的概念和战略地位（1）概念：所谓电⼦政务，就是国家政府部门以信息⽹络为平台，综合运⽤信息技术，将其管理和服务职能通过⽹络技术进⾏集成，在⽹络上实现政府组织结构和⼯作流程的优化重组，超越时间、空间、部门间隔的制约，全⽅位的向社会提供优质、规范、透明、符合国家标准的管理和服务。

实现公务、政务、商务的⼀体化运作和管理。

（2）战略地位：①以信息化带动⼯业化②政府先⾏，带动信息化发展③推⾏电⼦政务，实现政府信息化2传统政务与电⼦政务的⽐较⼀、带来全新的时空观⼆、集成化三、⾃动化、智能化四、个性化（具体见下表）★政府与政府间的电⼦政务(G2G)内容包括：①电⼦法规政策系统②电⼦公⽂系统③电⼦办公系统④电⼦司法档案系统⑤电⼦财政管理系统⑥电⼦培训系统⑦业绩评价系统★政府与企业之间的政务（G2B ）内容包括：①电⼦采购与招标②电⼦化报税③电⼦证照办理与审批④信息咨询服务★政府与公众间电⼦政务（G2C）内容包括：①教育培训服务②就业服务③电⼦医疗服务④社会保险⽹络服务⑤公民信息服务⑥交通管理服务⑦公民电⼦税务申报服务⑧电⼦证件服务5美国现在门户⽹站⽹址：6我国电⼦政务发展史(1)摸索阶段：20世纪90年代初——2002年；特点：建设⽐较零散，缺乏统⼀的战略规划，应⽤⽔平相对较低。

(2)发展阶段：2002年——2005年(3)成熟阶段:2006年——现在；标志：o6年⼏个重要纲领性⽂件的颁布，如1⽉1⽇⼈民政府⽹站正式开通，标志着我国从上⽽下政府⽹站体系基本确⽴；3⽉印发的《2006——2020年国家信息化发展战略》和《电⼦政务总体框架》7、⼀站两⽹四库⼗⼆⾦⼀站：政府门户⽹站两⽹：政府内⽹和外⽹四库：⼈⼝；法⼈单位；空间地理和⾃然资源；宏观经济⼗⼆⾦：⼀类：对加强监管、提⾼效率和推进公共服务起到核⼼作⽤的办公业务资源系统宏观经济管理系统建设；⼆类：增强政府收⼊能⼒、保证公共⽀出合理性的⾦税、⾦关、⾦财、⾦融监管、⾦审；三类：保障社会秩序，为国民经济和社会发展打下坚实的⾦盾、社会保障、⾦农、⾦⽔⾦质；8、内⽹：机关内部办公⽹,以局域⽹为基础，主要运⾏党政决策指挥系统、关键业务管理系统、核⼼数据应⽤系统、领导事务管理系统、涉及内部核⼼机密的应⽤系统、涉及重⼤事件的决策系统、涉及重要事务的核⼼信息数据管理系统；与互联⽹实⾏物理隔离。

企业uc矩阵图分析报告引言UC矩阵图（Use Case Matrix）是一种用于分析企业的业务流程和需求的工具。

通过使用UC矩阵图，企业可以分析各个业务功能的相关性和依赖关系，从而更好地规划和管理企业的信息系统。

本报告将以XYZ公司为例，通过对其UC矩阵图进行分析，帮助该公司发现潜在的问题和改进方向，进而优化其业务流程和信息系统。

分析结果UC矩阵图概述在进行UC矩阵图分析之前，我们首先需要对UC矩阵图做一个概述。

UC矩阵图由两个维度组成：Use Case（用例）和Actor（参与者）。

用例表示企业的业务功能，参与者表示与这些功能相关的角色或者系统。

矩阵的行代表了用例，列代表了参与者。

通过对矩阵中每个单元格的填充，可以表示用例和参与者之间的关系。

XYZ公司UC矩阵图分析在对XYZ公司的UC矩阵图进行分析之前，我们首先需要收集相关的信息。

通过与该公司的管理人员和业务人员沟通，我们获得了以下数据：用例参与者1 参与者2 参与者3 参与者4用例1 Y N Y N用例2 N Y Y N用例3 Y Y N N用例4 N N N Y用例5 Y N N Y通过填充UC矩阵图，我们可以得到以下结果：用例参与者1 参与者2 参与者3 参与者4用例1 Y N Y N用例2 N Y Y N用例3 Y Y N N用例4 N N N Y用例5 Y N N Y参与者关系分析参与者1在用例1、用例3和用例5中都有参与，说明其在这些用例中扮演了重要的角色。

参与者2在用例2和用例3中有参与，说明其在这些用例中也扮演了重要的角色。

参与者3只在用例1和用例2中有参与，但其在用例中所扮演的角色相对较小。

参与者4只在用例4和用例5中有参与，可能是用于某些特定功能的系统。

用例关系分析通过查看UC矩阵图，我们可以发现用例1和用例3具有一定的相关性，因为这两个用例都是参与者1和参与者3共同参与的。

这表明，在改进用例1的同时，也需要考虑用例3的相关性。

问题●斯塔林工业公司是一家资产达200 000 000美元的纺织品制造公司，数据处理主管罗格斯已经在公司呆了20年。

大多数已经开发的信息系统使用的都是传统文件。

由于许多系统是逐个开发的，所以许多有关客户、产品、厂商和订单的数据项被分别存储在不同的数据库中。

公司的管理者们需要开发一个用于销售和分配领域的新的应用软件。

现在主要的需求是将传统的批处理订货登记系统和库存控制系统向联机系统转化。

但实际上每个部门的管理者都有自己的关键需求，并且都对现在的已经积压了5年的信息系统开发项目很不耐烦。

●阐述你将如何利用BSP法解决该公司所遇到的这些问题？●在你的方案中，要对研究的步骤和结果进行描述。

●在方案实施过程中，数据处理主管和用户管理部门应担当何种角色、履行何种职责？●使用BSP法对你们组选定的企业的主要企业过程、主要数据类进行识别，并以此为依据确定信息结构1、BSP法解决该公司所遇到的问题1、首先，由各部门负责人参与组建委员会，从企业目标入手，认真讨论现有系统存在的问题，和希望新系统达到的目标，以及用户的期望等反复研究确定最终目标，该目标应与企业目标一致，要能表达所有管理层次的要求，并且能向企业提供一致性信息，对组织机构的变革具有适应性。

这即是把企业目标转化为信息系统战略。

根据题目信息可以判断，该公司的系统不够统一，许多数据的分散和冗余导致对业务的处理和库存的控制非常困难，而且不够准确，批处理系统的效率又比较低，必须设计一个比较系统的IS来管理公司的业务和库存等，要求该系统要有统一的数据源来管理公司各部门的数据，随着企业的发展传统的批处理系统已难以满足企业需求，只有对数据统一管理才能更好的实现实时系统，更好的提高企业运行的效率，2.然后，根据分析目标确定出未来信息系统的总体结构，明确系统的子系统组成和开发子系统的先后顺序。

对数据进行统一规划、管理和控制，明确各子系统之间的数据交换关系，保证信息的一致性。

3、BSP法设计的新系统能保证信息系统独立于企业的组织机构，使信息系统具有对环境变更的适应性。

3．5实验题
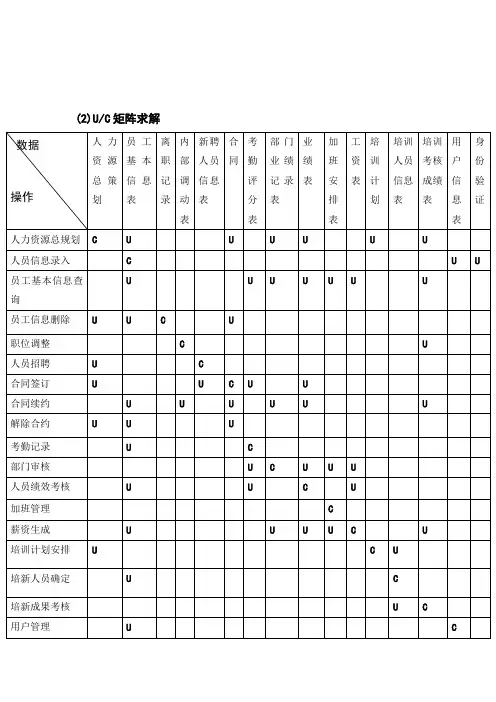
（2）参考本章例子，设计一个例子，说明U/C矩阵的模块划分的方法
图1既是初始的矩阵图，数据类和企业过程是随机排列的，U、C在矩阵中的排列也是分散的。

我们以调换企业过程和数据类的顺序的方法尽量使UC集中到对角线上排列，既是调换矩阵的行列顺序，使得C尽量地靠近对角线，如图2所示；沿着对角线划分模块，即将C和与之紧密联系的U画在一个框中，这些框便构成了系统的功能模块，这些小模块就是一个个小系统。

图2 调整行列并形成模块
图2既是划分好的模块，从上往下依次是经营计划子系统、产品研发子系统、生产制造计划子系统、销售子系统、财务子系统和人事档案子系统。

一、概述在数学和计算机领域中，解决三元一次方程是一个常见的问题。

在计算机图形学中，使用三维矩阵进行变换和投影时，常常需要解决三元一次方程。

为了提高计算效率和精度，我们可以利用Unity引擎中的矩阵快速求解方法来解决这一问题。

本文将介绍如何使用Unity引擎中的矩阵快速求解方法来解决三元一次方程，并给出相应的代码。

二、三元一次方程的求解三元一次方程是指形如ax + by + cz = d的方程，其中a、b、c、d 为已知常数，x、y、z为未知数。

解决三元一次方程的一种常见方法是利用矩阵的求解，通过矩阵运算来得到方程的解。

在Unity引擎中，我们可以利用矩阵的快速求解方法来进行计算。

三、Unity矩阵的快速求解方法Unity引擎中提供了Matrix4x4结构来表示4x4的矩阵，该矩阵结构包含了一系列的方法来进行矩阵的运算和求解。

通过调用Matrix4x4的方法，我们可以快速地求解三元一次方程。

四、代码实现下面是使用Unity引擎中矩阵快速求解方法来解决三元一次方程的示例代码：```csharpusing UnityEngine;public class EquationSolver : MonoBehaviour{void Start(){// 初始化系数矩阵Matrix4x4 coefficientMatrix = new Matrix4x4(new Vector4(1, 2, 3, 4),new Vector4(2, 3, 4, 5),new Vector4(3, 4, 5, 6),new Vector4(4, 5, 6, 7));// 初始化常数向量Vector4 constantVector = new Vector4(10, 11, 12, 13);// 求解方程Vector4 solution = coefficientMatrix.inverse * constantVector;// 输出结果Debug.Log("The solution is: " + solution);}}```以上代码通过Matrix4x4结构来表示系数矩阵和常数向量，并利用.inverse方法来求解方程。

1
U/C矩阵求解
例1：请对表1给出的U/C矩阵进行检验并求解，最后解释解的实际意义。

表1 某企业管理信息系统的U/C矩阵
解：
（1）U/C矩阵的正确性检验
建立U/C矩阵后要根据“数据守恒”原则进行检验。

经检验可得，第1列“客户”类缺少产生者(“C”)，第5列“物料清单”类和第7列“质量标准”类有两个产生者(“C”)，不满足完备性和一致性要求。

结合题意改进如下：
●第1行第1列的“U”改为“C”
●第3行第5列的“C”和第8行第7列的“C”改为“U”
（2）U/C矩阵的求解
通过调换“功能”和“数据类”的位置，使矩阵中的“C”尽量朝对角线靠近，并以“C”为标准划分子系统，得到结果如表2所示。

表2 求解后的U/C矩阵
（3）U/C矩阵的解给出了新系统的总体结构与数据联系。

因此，本系统可划分为产品管理、材料管理、生产管理、人事管理四个子系统，各子系统包含的功能以及子系统之间的数据联系如表3所示。

表3 划分子系统。