一元线性回归方程的计算和检验

12．9 一元线性回归以前我们所研究的函数关系是完全确定的，但在实际问题中，常常会遇到两个变量之间具有密切关系却又不能用一个确定的数学式子表达，这种非确定性的关系称为相关关系。

通过大量的试验和观察，用统计的方法找到试验结果的统计规律，这种方法称为回归分析。

一元回归分析是研究两个变量之间的相关关系的方法。

如果两个变量之间的关系是线性的，这就是一元线性回归问题。

一元线性回归问题主要分以下三个方面：（1）通过对大量试验数据的分析、处理，得到两个变量之间的经验公式即一元线性回归方程。

（2）对经验公式的可信程度进行检验，判断经验公式是否可信。

（3）利用已建立的经验公式，进行预测和控制。

12．9．1 一元线性回归方程 1．散点图与回归直线在一元线性回归分析里，主要是考察随机变量y 与普通变量x 之间的关系。

通过试验，可得到x 、y 的若干对实测数据，将这些数据在坐标系中描绘出来，所得到的图叫做散点图。

例1 在硝酸钠（NaNO 3）的溶解度试验中，测得在不同温度x （℃）下，溶解于100解 将每对观察值（x i ，y i ）在直角坐标系中描出，得散点图如图12.11所示。

从图12.11可看出，这些点虽不在一条直线上，但都在一条直线附近。

于是，很自然会想到用一条直线来近似地表示x 与y 之间的关系，这条直线的方程就叫做y 对x 的一元线性回归方程。

设这条直线的方程为yˆ=a+bx 其中a 、b 叫做回归系数（y ˆ表示直线上y 的值与实际值y i 不同）。

图12.11下面是怎样确定a 和b ，使直线总的看来最靠近这几个点。

2．最小二乘法与回归方程在一次试验中，取得n 对数据（x i ，y i ），其中y i 是随机变量y 对应于x i 的观察值。

我们所要求的直线应该是使所有︱y i －yˆ︱之和最小的一条直线，其中i y ˆ=a+bx i 。

由于绝对值在处理上比较麻烦，所以用平方和来代替，即要求a 、b 的值使Q=21)ˆ(i ni iyy-∑=最小。

《土地利用规划学》一元线性回归分析学院：资源与环境学院班级：2013009姓名：x学号：201300926指导老师：x目录一、根据数据绘制散点图： (1)二、用最小二乘法确定回归直线方程的参数： (1)1）最小二乘法原理 (1)2）求回归直线方程的步骤 (3)三、回归模型的检验： (4)1）拟合优度检验（R2）： (4)2）相关系数显著性检验： (5)3）回归方程的显著性检验（F 检验） (6)四、用excel进行回归分析 (7)五、总结 (15)一、根据数据绘制散点图：◎由上述数据，以销售额为y 轴（因变量），广告支出为X 轴（自变量）在EXCEL 可以绘制散点图如下图：◎从散点图的形态来看，广告支出与销售额之间似乎存在正的线性相关关系。

大致分布在某条直线附近。

所以假设回归方程为：x y βα+=二、用最小二乘法确定回归直线方程的参数： 1）最小二乘法原理年份 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 广告支出（万元）x 4.00 7.00 9.00 12.00 14.00 17.00 20.00 22.00 25.00 27.00销售额y7.00 12.00 17.00 20.00 23.00 26.00 29.00 32.00 35.00 40.00最小二乘法原理可以从一组测定的数据中寻求变量之间的依赖关系，这种函数关系称为经验公式。

考虑函数y=ax+b ，其中a,b 为待定常数。

如果Pi(xi,yi)（i=1,2,...,n ）在一条直线上，则可以认为变量之间的关系为y=ax+b 。

但一般说来, 这些点不可能在同一直线上. 记Ei=yi-(axi+b)，它反映了用直线y=ax+b 来描述x=xi ，y=yi 时，计算值y 与实际值yi 的偏差。

当然，要求偏差越小越好，但由于Ei 可正可负，所以不能认为当∑Ei=0时，函数y=ax+b 就好好地反应了变量之间的关系，因为可能每个偏差的绝对值都很大。

1. 从input 语句键盘输入一组数据（x i ，y i ），i=1，2,…n 。

2。

计算一元线性回归方程y=ax+b 的系数a 和b,用两种方法计算:一是公式:x a y b x x y y x x a iii -=---=∑∑,)())((2; 二是用最小二乘法的公式求出最小值点（a,b)，使∑--=2)(min },(b ax y b a Q i i3。

检验回归方程是否有效（用F 分布检验）。

4. 把散列点（x i ，y i )和回归曲线y=ax+b 画在一个图上。

5. 每种计算法都要有计算框图，且每种计算法都要编成一个自定义函数。

function yiyuanclc;disp （'从键盘输入一组数据：'）；x=input （'please Input data x ：’)；y=input （’please Input data y:')；disp(’一元线性回归的计算和检验:’）;disp （'1。

公式法’);disp （'2.最小二乘')；disp （'3.检验'）;disp(’0。

退出’)；global a0 b0;while 3num=input （'选择求解的方法:'）;switch numcase 1［a0,b0］=huigui （x,y)case 2[a0，b0］=zxec （x ，y ）case 3break;case 0return;otherwisedisp(’输入错误，请重先输入！')；endendX=x'；Y=y'；X=［ones(size （X)）,X ］；alpha=0.5；［b ，bint ，e ，rint,stats ］=regress(Y ,X)if stats(3）〈alphadisp （'有效的x ’）endn=［min(x):0.1：max(x ）]；f=a0*n+b0；xlabel(’x'，'b'）；ylabel('y’，’r’);legend（'散点’，’k')；end％..。

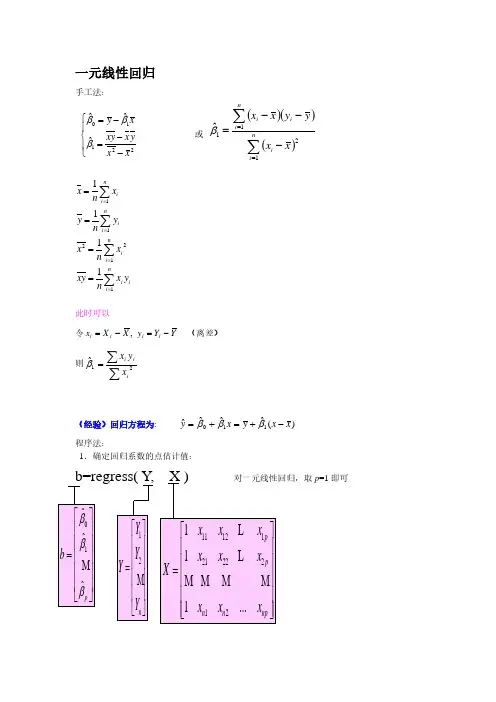
一元线性回归手工法：⎪⎩⎪⎨⎧−−=−=22110ˆˆˆx x y x xy x y βββ 或 ()()()∑∑==−−−=ni ini i ix xy y x x1211ˆβini i n i ini ini iy x n xy x n x y n y x n x ∑∑∑∑========1122111111 此时可以令Y Y y X X x i i i i −=−= , （离差）则∑∑=21ˆiii xy x β（经验）回归方程为: )(ˆˆˆˆ110x x y x y −+=+=βββ 程序法：1．确定回归系数的点估计值：b=regress( Y , X ) 对一元线性回归，取p =1即可01ˆˆˆp b βββ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦M 12n Y Y Y Y ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦M 111212122212111...p p n n np x x x x x x X x x x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L M M M M程序数据的输入可以参考如下：x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x];Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';2．回归分析及检验：[b,bint,r,rint,stats]=regress(Y ,X)b,bint,stats得结果：b = bint =-16.0730 -33.7071 1.5612 0.7194 0.6047 0.8340 stats =0.9282 180.9531 0.0000即7194.0ˆ,073.16ˆ10=−=ββ；0ˆβ的置信区间为[-33.7017，1.5612], 1ˆβ的置信区间为[0.6047,0.834]; r 2=0.9282, F =180.9531, p =0.0000 p <0.05, 可知回归模型 y =-16.073+0.7194x 成立.这个程序可以进行，第一步的拟合优度与相关系数检验， 第三步的方程的整体性检验（F 检验） ，因此第一步的拟合优度 r 平方已算出就根据 r 2 =1意味着完全拟合，r 2 =0意味着被解释变量与解释变量之间没有线性关系，0< r 2 <1时，r 2越接近于1拟合效果越好。

一元线性回归一、一元线性回归模型的数学形式εββ++=x y 10 对两边求数学期望和方差得：i i x y E 10)(ββ+=，2)var(σ=i y 随机变量y 的期望不等，方差相等，因而i y 是独立随机变量，但并不同分布，而i ε是独立同分布的随机变量。

估计参数1ˆβ在实际应用中表示自变量x 每增加一个单位时因变量y 平均增加数量。

一元回归的一般形式用矩阵表示：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n y y y y 21，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x x 21111，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n εεεε 21，⎥⎦⎤⎢⎣⎡=10βββ，模型表示有：⎪⎩⎪⎨⎧I ==+=n E x y 2)var(0)(σεεεβ 其中n I 为n 阶单位矩阵。

二、参数估计需注意，极大似然估计是在),0(~2σεN i 的正态分布假设下求得的，而最小二乘估计则对分布假设没有要求，另外，n y y y ,,,21 是独立的正态分布样本，但并不是同分布的，期望值i i x y E 10)(ββ+=不相等。

三、最小二乘估计的性质1、线性性：估计量10ˆ,ˆββ为随机变量i y 的线性函数2、无偏性：yˆ,ˆ,ˆ01ββ是y ,,01ββ无偏估计 3、10ˆ,ˆββ的方差∑∑∑===-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=nj jini n j j i x x y x x x x 12212121)()var()()ˆvar(σβ，21220)()(1)ˆvar(σβ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+=∑=ni i x x x n从上面两个式子可以看出，要想使10,ββ的估计值10ˆ,ˆββ更稳定，在收集数据时，就应该考虑x 的取值尽可能分散一些，不要挤在一块，样本量应尽可能大一些，样本量n 太小时估计量的稳定性肯定不会太好。

从))(1,(~ˆ2200σββ⎥⎦⎤⎢⎣⎡+xxL x nN ;),(~ˆ211xxL N σββ;其中∑=-=ni ixx x xL 12)(可以得到：210)ˆ,ˆcov(σββxxL x -=，在x =0时，10ˆ,ˆββ的协方差为0，此时10ˆ,ˆββ不相关，在正态假定下独立；在≠x 0时不独立。

一元线性回归效果的显著性检验(F检验法)前面我们给出了一元回归直线方程的求解即一元线性回归中未知参数的最小二乘估计．那么这条回归直线对观测数据(x i,y i) (i=1,2,…,n) 拟合的程度如何？是否真正体现x、y 之间的这种线性关系，这就需要对回归效果的好坏进行检验．这种检验是评价方程对总体的代表性的所谓线性关系的显著性检验．检验x与y是否具有线性关系，以及它们之间的密切程度，这就是回归直线方程的效果检验所要解决的问题．由一元线性回归的数学模型可知，一元线性回归的数学模型是y=a+bx+εε～N(0, σ2)即随机变量y的数学期望是自变量x的线性函数，然而这样的假设是否合理呢？若在y=a+bx+ε中b=0，说明x的变化对y没有影响，这时回归方程就不能近似地描述变量x与y之间的关系，因此为了判断x与y之间是否存在线性关系，只需检验假设：H0：b=0此问题也称为线性回归方程的显著性检验问题．我们要根据观测数据(x i,y i) (i=1,2,…,n)作出拒绝或接受原假设b=0的判断．拒绝原假设才能确认我们的线性回归模型是合理的，接受原假设表示不能认为x、y之间有线性相关关系．如何构造统计量来检验这个假设问题呢？我们先把变量y的离差平方和予以分解.（点击此处看分解过程）=Q+U其中是回归值与其平均值的离差平方和，而,可以把看成是由于x的变化而引起的y值变化，因此称之为回归平方和；反映的是观测值与回归值之间的离差平方和，它表示除x对y的线性影响之外的一切因素引起的y值的变化，称之为误差平方和或残差平方和.而∴数学上我们可以证明,当H0为真时,统计量～F(1, n-2).对于给定的显著性水平α,查自由度为(1，n-2)的F分布临界值表,可得临界值Fα(1, n-2) 使得.其拒绝域为W={F>Fα(1, n-2)}.例在某大学一年级新生体检表中,随机抽取10张,得到10名大学生的身高(x)和体重(y)的数据如下,试求体重关于身高的线性回归方程,并检验回归方程的显著性(α=0.05)?身高x i/cm 体重y i/kg 身高x i/cm 体重y i/kg162 170 166 158 174 51545247631661671701731685955605754解.根据表中数据,列出下列计算表. 回归直线方程的计算步骤(I)i x i y i x i2y i 2x i y i1 2 3 4 5 6 7 8 9 10 Σ1621701661581741661671701731681674515452476359556057545522624428900275562496430276275562788928900299292822428043826012916270422093969348130253600324929163067082629180863274261096297949185102009861907292574,,,,,∴,.因此线性回归方程为:.下面我们来检验身高x与体重y之间是否具有显著的线性关系．根据题意,我们作假设H0: b=0 . n=10 ,,,∴.对于给定的α=0.05,查F分布临界值表得到临界值:F0.05(1, 8)=5.32．显然，F0=19.12> F0.05(1, 8)=5.32，故拒绝H0，即由F检验法可知，身高x与体重y 之间的线性关系是显著的，且它们之间的关系为：.。

从统计学看线性回归（2）——⼀元线性回归⽅程的显著性检验⽬录1. σ2 的估计2. 回归⽅程的显著性检验 t 检验（回归系数的检验） F 检验（回归⽅程的检验） 相关系数的显著性检验 样本决定系数 三种检验的关系⼀、σ2 的估计 因为假设检验以及构造与回归模型有关的区间估计都需要σ2的估计量，所以先对σ2作估计。

通过残差平⽅和（误差平⽅和）（1）（⽤到和，其中）⼜∵（2）∴（3）其中为响应变量观测值的校正平⽅和。

残差平⽅和有n-2 个⾃由度，因为两个⾃由度与得到的估计值与相关。

（4）（公式（4）在《线性回归分析导论》附录C.3有证明）∴σ2的⽆偏估计量：（5）为残差均⽅，的平⽅根称为回归标准误差，与响应变量y 具有相同的单位。

因为σ2取决于残差平⽅和，所以任何对模型误差假设的违背或对模型形式的误设都可能严重破坏σ2的估计值的实⽤性。

因为由回归模型残差算得，称σ2的估计值是模型依赖的。

⼆、回归⽅程的显著性检验 ⽬的：检验是否真正描述了变量 y 与 x 之间的统计规律性。

假设：正态性假设（⽅便检验计算）1. t 检验 ⽤t 检验来检验回归系数的显著性。

采⽤的假设如下：原假设 H0：β1 = 0 （x 与 y 不存在线性关系）对⽴假设 H1：β1 ≠ 0 回归系数的显著性检验就是要检验⾃变量 x 对因变量 y 的影响程度是否显著。

下⾯我们分析接受和拒绝原假设的意义。

（1）接受 H0：β1 = 0 （x 与 y 不存在线性关系） 此时有两种情况，⼀种是⽆论 x 取值如何， y 都在⼀条⽔平线上下波动，即，如下图1，另⼀种情况为， x 与 y 之间存在关系，但不是线性关系，如图2。

图 1图 2 （2）拒绝 H0：β1 = 0 （x 对解释 y 的⽅差是有⽤的） 拒绝原假设也有两种情况，⼀种是直线模型就是合适的，如图 3，另⼀种情况为存在 x 对 y 的线性影响，也可通过 x 的⾼阶多项式得到更好的结果，如图 4。

计量经济学第二章一元线性回归模型第二章一元线性回归模型第一节一元线性回归模型及其古典假定第二节参数估计第三节最小二乘估计量的统计特性第四节统计显著性检验第五节预测与控制第一节回归模型的一般描述（1）确定性关系或函数关系：变量之间有唯一确定性的函数关系。

其一般表现形式为：一、回归模型的一般形式变量间的关系经济变量之间的关系，大体可分为两类：（2.1)（2）统计关系或相关关系：变量之间为非确定性依赖关系。

其一般表现形式为：(2.2)例如：函数关系：圆面积S =统计依赖关系/统计相关关系：若x和y之间确有因果关系，则称(2.2)为总体回归模型，x(一个或几个）为自变量（或解释变量或外生变量），y为因变量（或被解释变量或内生变量），u为随机项，是没有包含在模型中的自变量和其他一些随机因素对y的总影响。

一般说来，随机项来自以下几个方面：1、变量的省略。

由于人们认识的局限不能穷尽所有的影响因素或由于受时间、费用、数据质量等制约而没有引入模型之中的对被解释变量有一定影响的自变量。

2、统计误差。

数据搜集中由于计量、计算、记录等导致的登记误差；或由样本信息推断总体信息时产生的代表性误差。

3、模型的设定误差。

如在模型构造时，非线性关系用线性模型描述了；复杂关系用简单模型描述了；此非线性关系用彼非线性模型描述了等等。

4、随机误差。

被解释变量还受一些不可控制的众多的、细小的偶然因素的影响。

若相互依赖的变量间没有因果关系，则称其有相关关系。

对变量间统计关系的分析主要是通过相关分析、方差分析或回归分析(regression analysis)来完成的。

他们各有特点、职责和分析范围。

相关分析和方差分析本身虽然可以独立的进行某些方面的数量分析，但在大多数情况下，则是和回归分析结合在一起，进行综合分析，作为回归分析方法的补充。

回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。

第二节一元线性回归分析本节主要内容：回归是分析变量之间关系类型的方法，按照变量之间的关系，回归分析分为：线性回归分析和非线性回归分析。

本节研究的是线性回归，即如何通过统计模型反映两个变量之间的线性依存关系.回归分析的主要内容:1.从样本数据出发，确定变量之间的数学关系式；2.估计回归模型参数；3.对确定的关系式进行各种统计检验,并从影响某一特定变量的诸多变量中找出影响显著的变量。

一、一元线性回归模型:一元线性模型是指两个变量x、y之间的直线因果关系。

理论回归模型:理论回归模型中的参数是未知的,但是在观察中我们通常用样本观察值估计参数值，通常用分别表示的估计值，即称回归估计模型：回归估计模型：二、模型参数估计：用最小二乘法估计：【例3】实测某地四周岁至十一岁女孩的七个年龄组的平均身高（单位：厘米）如下表所示某地女孩身高的实测数据建立身高与年龄的线性回归方程。

根据上面公式求出b0=80。

84，b1=4。

68。

三．回归系数的含义（2）回归方程中的两个回归系数，其中b0为回归直线的启动值，在相关图上变现为x=0时，纵轴上的一个点,称为y截距；b1是回归直线的斜率，它是自变量(x）每变动一个单位量时，因变量（y）的平均变化量。

（3）回归系数b1的取值有正负号。

如果b1为正值，则表示两个变量为正相关关系,如果b1为负值，则表示两个变量为负相关关系。

[例题·判断题］回归系数b的符号与相关系数r的符号，可以相同也可以不同.（ )答案：错误解析：回归系数b的符号与相关系数r的符号是相同的=a+bx，b<0，则x与y之间的相关系数（ )［例题·判断题]在回归直线yca。

r=0 b.r=1 c。

0<r〈1 d.—1<r〈0答案:d解析：b〈0,则x与y之间的相关系数为负即—1〈r〈0［例题·单选题］回归系数和相关系数的符号是一致的，其符号均可用来判断现象( ）a。

线性相关还是非线性相关 b.正相关还是负相关c。