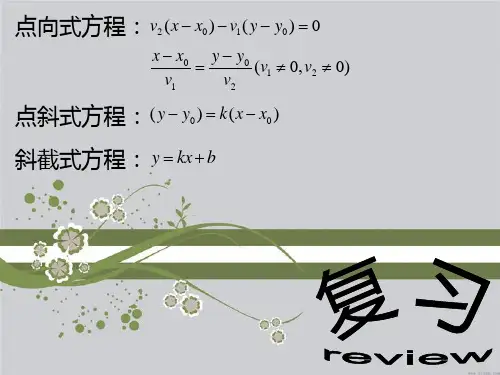
直线的点向式方程

三维空间中的直线方程表达式
在三维空间中，一条直线可以用参数方程或者点向式来表示。

其中，参数方程是指用一个参数表示直线上的所有点，而点向式则是指用一个起点和一个方向向量来表示直线。

参数方程可以用以下公式表示：
x = x_0 + at
y = y_0 + bt
z = z_0 + ct
其中，(x_0, y_0, z_0)是直线上的某一点，而(a, b, c)则是直线的方向向量，t为参数。

点向式可以用以下公式表示：
r = a + tb
其中，a为直线的起点，b为直线的方向向量，而r为直线上的任一点，t为参数。

需要注意的是，当直线平行于坐标轴时，可以用一般式方程来表示：
Ax + By + Cz + D = 0
其中，(A, B, C)为直线的方向向量的系数，而D则是常数项。

使用这些方程可以方便地求解三维空间中的直线问题，比如求直线与平面的交点、直线的距离等。

- 1 -。

三维空间中直线的方程式在三维空间中，直线的方程可以用参数方程和一般方程两种形式表示。

参数方程是将直线上的每一个点都表示为一个参数所确定的向量，而一般方程则是通过直线上两个点的坐标来表示的。

1.参数方程：直线的参数方程可以表示为：x = x0 + aty = y0 + btz = z0 + ct其中(x0,y0,z0)为直线上的已知点，而(a,b,c)为直线的方向向量，t为参数。

2.一般方程：首先，我们需要确定直线的方向向量。

假设直线上的两个点分别为P(x1,y1,z1)和Q(x2,y2,z2)，则直线的方向向量可以表示为V=PQ=(x2-x1,y2-y1,z2-z1)。

然后，我们可以通过点P的坐标和方向向量V来推导直线的一般方程。

2.1.点向式：直线的一般方程可以表示为：(x-x1)/a=(y-y1)/b=(z-z1)/c其中(a,b,c)为方向向量V的分量。

2.2.对称式：直线的一般方程也可以表示为：(x-x1)/a=(y-y1)/b=(z-z1)/c=t这里的t为参数。

2.3.常法式：直线的一般方程还可以表示为：Ax+By+Cz+D=0其中A,B,C为方向向量V的分量，而D为常数。

对于两个不平行的直线，我们可以通过将它们的方向向量进行叉乘来求得它们的交点。

除了参数方程和一般方程，还有其他表示直线的方法，比如点法式、斜截式等。

这些方法都根据直线上已知点和方向向量的不同形式而有所不同。

需要注意的是，在使用直线的方程时，我们需要根据实际情况选择最适合的表达形式。

有时候参数方程更方便，可以直接通过改变参数t来表示直线上的任意一点；而一般方程则适合于求直线与其他平面或直线的交点等问题。

【初中数学】初中数学直线的方程公式【—直线的方程公式】我们在初中学习的直线的方程包括有平面方程和空间方程两种，相较于空间方程来说，平面方程的运用比较的多。

直线的方程平面方程1、一般式：适用于所有直线ax+by+c=0(其中a、b不同时为0)2、点斜式：知道直线上一点(x0，y0)，并且直线的斜率k存在，则直线可表示为y-y0=k(x-x0)当k不存在时，直线可表示为x=x03、斜截式：在y轴上截距为b(即过(0，b))，斜率为k的直线由点斜式只须斜截式y=kx+b与点斜式一样，也需要考虑k存不存在4、dT式：呼吸困难用作和任一坐标轴横向的直线知道直线与x轴交于(a，0)，与y轴交于(0，b)，则直线可表示为bx+ay-ab=0特别地，当ab均不为0时，斜截式可写为x/a+y/b=15、两点式：过(x1，y1)(x2，y2)的直线(y-y1)/(y1-y2)=(x-x1)/(x1-x2)(斜率k需存在)6、法线式xcosθ+ysinθ-p=0其中p为原点至直线的距离，θ为法线与x轴正方向的夹角7、点方向式(x-x0)/u=(y-y0)/v(u，v不等同于0，即点方向式无法则表示与座标平行的式子)8、点法向式a(x-x0)+b(y-y0)=0空间方程1、通常式ax+bz+c=0,dy+ez+fc=02、点向式：设直线方向向量为(u,v,w)，经过点(x0,y0,z0)(x-x0)/u=(y-y0)/v=(x-x0)/w3、x0y式x=kz+b,y=lz+b总结归纳一共有11个直线的方程公式，要运用好的时候也请大家选择了。

空间直线点向式方程和一般方程的相互转化数学中，空间直线的表示方式有很多种，其中最常见的有直线的向式方程和一般方程。

这两种方程之间的相互转化在数学中有着广泛的应用。

本文将从向式方程和一般方程的基本概念、转化方法等方面进行介绍。

一、向式方程的基本概念向式方程是指通过直线上一点和直线的方向向量，来表示直线的方程。

具体来说，若直线L上有点P（x0,y0,z0），且直线的方向向量为a（a1,a2,a3），则直线的向式方程可以表示为：(x-x0)/a1 = (y-y0)/a2 = (z-z0)/a3其中，x、y、z分别表示直线上任意一点的坐标。

二、一般方程的基本概念一般方程是指通过直线上两个不同的点来表示直线的方程。

具体来说，若直线L上有两点P1（x1,y1,z1）和P2（x2,y2,z2），则直线的一般方程可以表示为：(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1)其中，x、y、z分别表示直线上任意一点的坐标。

三、向式方程和一般方程的相互转化在数学中，向式方程和一般方程是可以相互转化的。

具体来说，有以下两种转化方式：1. 从向式方程转化为一般方程若已知直线L的向式方程为：(x-x0)/a1 = (y-y0)/a2 = (z-z0)/a3我们可以通过以下步骤将其转化为一般方程：（1）将向量a化为平面上的两个向量b和c。

具体来说，我们可以任意选取两个向量b和c，使它们与向量a不共线，然后使用向量叉积的方法求出向量n=b×c（其中×表示向量叉积）。

向量n垂直于平面，而既过点P且平行于向量a的直线L，则与平面到点P的垂线n相交于点Q，可以把向量PQ看成是平面上的向量，其分别在b、c上的投影值分别为t和s（t和s为实数）。

因此，我们可以得到以下向量表示：PQ = tb+sc（2）将向量表示化为坐标表示，具体来说，我们可以将向量b、c和n 分别表示为坐标向量：b = (x1,y1,z1)c = (x2,y2,z2) n = (a1,a2,a3)则有：PQ = tb+sc = (x-x0,y-y0,z-z0)因此，我们可以得到以下解方程组的方法：(x-x0)/a1 = (y-y0)/a2 = (z-z0)/a3(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1)2. 从一般方程转化为向式方程若已知直线L的一般方程为：(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1)我们可以通过以下步骤将其转化为向式方程：（1）选取一点P(x0,y0,z0)在直线上，我们假设刚刚选取的点为P(x0,y0,z0)。

空间直线点法式空间直线是三维空间中的一条线段，由两个点所确定。

空间直线的参数方程可以用点和向量的形式表示，又称为向量方程。

空间直线还可以用点和点的形式表示，又称为点法式或一般方程。

为了方便描述，我们假设空间直线L平面上的一点为P0(x0,y0,z0)，空间直线L的方向向量为a(x1,y1,z1)。

一、点向式空间直线L的点法式可以表示成如下形式：(x-x0)/x1 = (y-y0)/y1 = (z-z0)/z1这种表示方法的含义是，设L上的点Q(x,y,z)，以P0点作为基准点，沿着方向向量a，假设走的距离为t（其中t为实数），则Q点的坐标可以用P0点的坐标和方向向量a的分量来表达，即：x=x0+tx1这样就得到了空间直线L的参数方程式。

二、一般式我们已经知道了点向式，现在来看一下空间直线的另一种表示方法——一般式。

其中，(A,B,C)为向量a的一个法向量。

这个式子怎么来的呢？我们可以将L上任一点P用向量形式表示，即P=P0+ta再将P带入空间直线L所在平面的解析式中，得到：(Ax1+By1+Cz1)-(Ax0+By0+Cz0)=0整理一下得到以上的一般式。

三、点向式和一般式的转换我们可以通过以下方式实现点向式和一般式的转换：1、从点向式转换为一般式：将点向式的分式形式变形，消去分母，即可得到一般式。

首先，把点向式中所有的“=”换为“-”，即得到以下形式：然后再将上述三个式子变形消去分母，得到一般式：(y1*z0-y0*z1)x+(x1*z0-x0*z1)y+(x0*y1-x1*y0)z+(x0*y1-x1*y0) = 02、从一般式转换为点向式：选取方向向量，利用向量的模长求分量，得到点向式。

首先，选取一个方向向量a(x1,y1,z1)，其中至少有一个分量不为零。

我们可以假设x1=1，则有：因为x1=1，所以y1和z1都不为零。

我们可以求出y1和z1的模长，然后再利用上式求出y和z的分量，即可得到点向式。

列出直线的参数式和点向式方程直线是平面几何中的基本概念之一，它可以由不同的方式进行表达，其中参数式和点向式方程是两种常见的表示方法。

本文将首先介绍直线的基本定义和性质，然后详细讨论参数式和点向式方程的推导和应用，最后总结两种表示方法的优缺点。

一、直线的基本定义和性质直线是由无数个点组成的，且它们之间的任意两点都可以用直线连接。

直线的特点是无宽度、无弯曲和无端点。

直线可延伸到无限远，这意味着它在两个方向上都是无限长的。

二、参数式方程参数式方程是一种通过参数表达直线方程的方法。

具体而言，参数式方程将直线上的每个点与参数相联系。

常见的参数式方程形式为：x = x₀ + mty = y₀ + nt其中，(x₀, y₀)是直线上的任意一点，m和n分别是x轴和y轴方向上的增量，t是参数，可以取任何实数值。

参数式方程的优点是可以方便地描述直线上的所有点，且易于进行计算，例如求两条直线的交点等。

三、点向式方程点向式方程又称为法向量方程，它通过直线上的一点和直线的法向量来表示直线方程。

具体而言，点向式方程的形式为：n · (r - r₀) = 0其中，r = (x, y)是直线上的任意一点，r₀ = (x₀, y₀)是直线上的已知点，n = (a, b)是直线的法向量。

点向式方程的优点是可以清晰地描述直线的法向量和已知点的关系，进而构建直线方程。

四、参数式方程与点向式方程的关系为了从参数式方程转化为点向式方程，我们需要先确定直线上一点和法向量。

设参数式方程为：x = x₀ + mty = y₀ + nt其中，m和n为参数，由于直线上的两个点分别为(x₀, y₀)和(x₁, y₁)，则可以计算出直线上的向量为：r = (x₁ - x₀, y₁ - y₀)进一步，我们可以取法向量为向量r的正交向量，即：n = (y₀ - y₁, x₁ - x₀)将直线上的已知点和法向量代入点向式方程，即可得到点向式方程的形式。

直线点向式方程公式
点向式方程是几何学中表示直线方程的一种形式，其一般形式为：(X-X0)/A = (Y-Y0)/B = (Z-Z0)/C。

其中，(X0,Y0,Z0)是直线上的一个已知点，A、B、C为直线的方向向量。

这个方程的特点是可以直接看出直线的方向以及直线上的一个点的坐标。

对于二维平面中的情况，点向式方程可以简化为：(x-x0)/a=(y-y0)/b，其中(a,b)为直线的方向向量，(x0,y0)为直线上的一个已知点。

当直线水平时，方向向量的纵坐标b为0，此时方程变为x=x0；当直线垂直时，方向向量的横坐标a为0，此时方程变为y=y0。

点向式方程常用于求解几何问题，如求两条直线的交点、判断一个点是否在直线上等。

同时，点向式方程也有许多变形，如参数式、斜截距式等，这些都能更方便地解决某些具体问题。

参考：百度文库
在三维空间中，点向式方程可以以更为一般的形式出现，既适用于直线，也可用于表示平面。

在表示平面时，可以将其理解为一个特定点（x0，y0，z0）与平面上任意一点（x，y，z）的向量与法向量之间的点积为零。

对此问题进行进一步研究，我们会发现点向式方程的广泛应用，如物体在三维空间中的旋转动作、光线穿过某一点的反射与折射等。

它其实是一种通用的数学描绘方式，不仅在初高中数学课本中广泛运用，在高等数学、线性代数等课程中也有重要应用。

借助它能够更全面、深入地理解直线与空间的关系，揭示了几何与数学的内在联系。

空间直线方程点向式转一般式
空间中的直线可以用不同的方式表示，其中一种方式是点向式，另一种是一般式。

下面将介绍如何将点向式转换为一般式。

点向式表示的直线可以写成如下形式：
$vec{r}=vec{a}+tvec{d}$
其中，$vec{a}$是直线上的一个点，$vec{d}$是直线的方向向量，$t$是实数。

一般式表示的直线可以写成如下形式：
$$frac{x-x_0}{l}=frac{y-y_0}{m}=frac{z-z_0}{n}$$ 其中，$(x_0,y_0,z_0)$是直线上的一个点，$l,m,n$是方向比例系数。

现在需要将点向式转换为一般式。

首先，由于直线上必须存在一个点，因此可以将点向式中的$vec{a}$代入一般式中，得到：
$$frac{x-a_x}{d_x}=frac{y-a_y}{d_y}=frac{z-a_z}{d_z}$$ 接下来，将等式两边分别乘以$d_x,d_y,d_z$，得到：
$$begin{cases} x-a_x=tcdot d_x+x_0 y-a_y=tcdot d_y+y_0 z-a_z=tcdot d_z+z_0 end{cases}$$
将上述三个式子代入一般式中，得到：
$$frac{x-x_0}{d_x}=frac{y-y_0}{d_y}=frac{z-z_0}{d_z}$$ 因此，点向式转一般式的方法如下：
1. 将点向式中的$vec{a}$代入一般式中；
2. 将等式两边分别乘以$d_x,d_y,d_z$；
3. 将代入后的三个式子代入一般式中，即可得到一般式。

三维直线拟合公式
在三维空间中，拟合一条直线的公式可以根据不同的表示方法而变化。

以下给出两种常用的方法：
一、直线方程的三种表示方法
1.一般式：它实际上表示，直线是两个平面的交线，因此可以由两个平面方程得到，
即：
Ax + By + Cz + D = 0
2.点向式（标准方程）：(m, n, p) 为直线方程的方向向量；(x0, y0, z0) 为直线上的一
个点。

m(x - x0) + n(y - y0) + p(z - z0) = 0
3.参数方程：由此就可以得到：
x = x0 + mt
y = y0 + nt
z = z0 + pt
其中(x0, y0, z0) 为直线上的一点，t 为参数。

二、利用最小二乘法拟合直线方程。

该方法的核心是利用离散点（实际点）与拟合
直线上的点（理想点）残差的平方和作为目标函数，求偏导计算最小值即可。

通过解多个点的矛盾方程，构建直线拟合经验公式：
y = a * x + b
在三维空间中，假设我们有一组三维点数据，其中每一个X均有一个Y与之对应，我们不妨构建矩阵，解矛盾方程求解即可。