下载文档原格式
多元函数微分学1、极限与连续性平面上的点列的极限：设{}n M 为平面点列，20M R ∈，若()0lim ,0n M M ρ=，则称{}n M 是收敛点列，0M 是点列的极限，记做0lim n n M M→∞=（00lim ,lim n n x x y y ⇔==）。
极限：设n 元函数()f P ，n P D R ∈⊂，0P 是D 的聚点，若存在常数A ，对0ε∀>，0,δ∃>对一切0(,δ)oP D U P ∈ ，有()f P A ε-<，则称常数A 为函数()f x 当0P P →时的极限，记做()0lim P P f P A →=（也叫n 重极限）。
二元函数的极限可写作：()()000,lim (,)lim (,)lim (,)x x x y x y y y f x y f x y f x y A ρ→→→→→===。
连续性：0M 为D 的聚点时，0lim ()()M M f M f M →=；或0M 为D 的孤立点时，也是连续点。
2、微分和偏导数微分：0000(,)(,)()f x x y y f x y A x B y o ρ+∆+∆-=∆+∆+⇒00(,)dz df x y A x B y ==∆+∆。
偏导数：设(),z f x y =在点()000,M x y 的某邻域中有极限00000(,)(,)lim x f x x y f x y x∆→+∆-∆（将y 当作常数）存在，则称此极限高 数多元函数微分学知识点速记为函数(),z f x y =在点()000,M x y 对x 的偏导数，即0000000(,)(,)(,)limx x f x x y f x y f x y x∆→+∆-'=∆；同理，函数(),z f x y =在点()000,M x y 对y 的偏导数0000000(,)(,)(,)limy y f x y y f x y f x y y∆→+∆-'=∆。
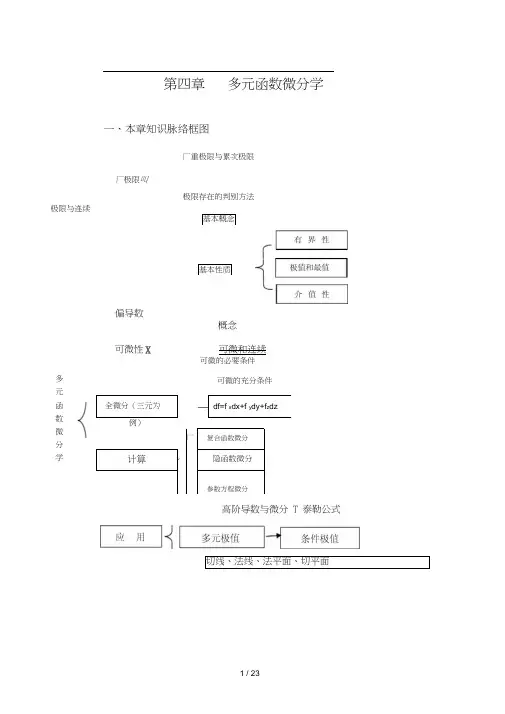
第四章多元函数微分学一、本章知识脉络框图厂重极限与累次极限厂极限叫极限存在的判别方法概念可微性X可微和连续可微的必要条件高阶导数与微分 T 泰勒公式切线、法线、法平面、切平面极限与连续基本概念基本性质偏导数多 元 函 数 微 分 学全微分（三元为→ df=f xdx+f ydy+f zdz例）厂复合函数微分计算V隐函数微分参数方程微分可微的充分条件二、本章重点及难点本章需要重点掌握以下几个方面内容：偏导数、全微分及其几何意义，可微与偏导存在、连续之间的关系，复合函数的偏导数与全微分，一阶微分形式不变性，方向导数与梯度，高阶偏导数，混合偏导数与顺序无关性，二元函数中值定理与Taylor公式.隐函数存在定理、隐函数组存在定理、隐函数（组）求导方法、反函数组与坐标变换几何应用（平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线极值问题（必要条件与充分条件），条件极值与Lagrange乘数法.三、本章的基本知识要点（一）平面点集与多元函数1. 任意一点A与任意点集E的关系•1）内点•若存在点A的某邻域U A ,使得U A］二E ,则称点A是点集E的内点。
2）外点•若存在点A的某邻域U A ,使得U A - E=N ,则称点A是点集E的外点。
3）界点（边界点）•若在点A的任何邻域内既含有属于E得的点，又含有不属于E的点，则称点A是点集E的界点。
4）聚点•若在点A的任何空心邻域U o A内部都含有E中的点，则称点A是点集E 的聚点。
5）孤立点.若点A E，但不是E的聚点，则称点A是点集E的孤立点。
2. 几种特殊的平面点集•1）开集•若平面点集E所属的每一点都是E的内点，则称E为开集。
2）闭集.若平面点集E的所有聚点都属于E，则称E为闭集。
3）开域.若非空开集E具有连通性，即E中任意两点之间都可用一条完全含于E得有限折线相连接，则称E为开域。
4）闭域.开域连同其边界所成的点集称为闭域。
5）区域.开域、闭域或者开域连同某一部分界点所成的点集，统称为区域。
