当前位置：文档之家 › 激光原理第4章

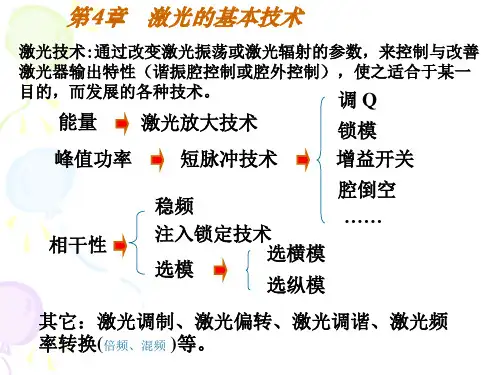
激光原理第4章

  • 格式：ppt
  • 大小：2.51 MB
  • 文档页数：63

下载文档原格式

  / 63

合集下载

激光原理、技术与应用课件：4_1_1 激光单纵模的选取

激光原理、技术与应用课件：4_1_1 激光单纵模的选取

3. 三反射镜法：
➢如图4-3所示，激光器一端的反射镜被三块反射镜的组合 所代替，其中M3和M4为全反射镜，M2是具有适当透射率 的部分透射部分反射镜。这个组合相当于两个谐振腔的耦 合
图4-3 三反射镜法
两个谐振腔的纵模频率间隔分别为：
v短
c
2（L2
L3）
v长
c
2（L1
L2）
只有同时满足上面两个谐振条件的光才能形成振荡，故只 要选取L2 +L3足够小，就可获得单纵模输出。
和单纵模光束。 因此，设计和改进激光器的谐振腔，抑制多模，以获得单模输出是一个
重要课题
4.1.1 激光单纵模的选取
所谓激光纵模选择，就是通过使激光器只允许有一种 频率振荡，而其余的频率则均被抑制。
一、均匀增宽型谱线的纵模竞争
核心问题:与饱和效应相关的模式之间的竞争！
回顾思考: 试说明某个频率的光最终要成为激光的 纵模输出，它必须突破几个关口。
➢缺点: 标准具总会带来透射损失对低增益 的激光器(He— Ne激光器）不合适， 但对高增益的激光器（CO2激光器） 则很有效。
四、使用腔内插入F-P标准具法选纵模需要注意：
1. 选择合适的标准具光学长度，使标准具的自由光谱范围
与激光器的增益线宽相当。使在增益线宽内，避免存在
两个或多个标准具的透过峰。
第4章 激光的基本技术
激光技术:通过改变激光振荡或激光辐射的参数，来控制与改善
激光器输出特性（谐振腔控制或腔外控制），使之适合于某一
目的，而发展的各种技术。
调Q
能量 激光放大技术
锁模
峰值功率 短脉冲技术
增益开关
相干性
腔倒空
稳频 注入锁定技术

激光原理 第四章-1激光器的振荡阈值

激光原理 第四章-1激光器的振荡阈值
Ppt h p nV 2 F s
h p V
1 21 ( , 0 )l
h p nV 21
n n2t 2
E pt
end
一 激光器的振荡阈值(threshold)

Operation at threshold 阈值反转集居数密度 阈值增益系数 连续或长脉冲激光器的阈值泵浦功率 短脉冲激光器的阈值泵浦能量
（一）阈值反转集居数密度 (population inversion density at threshold)

能否产生振荡，取决于增益与损耗的大小。 谐振腔的长度L往往大于工作物质的长度l， 假设谐振腔中光束体积为VR，工作物质中的 光束体积为Va，谐振腔中折射率均匀分布， 则第l个模式的光子数变化的方程
L为谐振腔 光程长度
c
d ( NlVR ) NlVR f2 (n2 n1 ) 21 ( , 0 ) NlVa dt f1 Rl
n nt 21 ( , 0 )l
0
• 不同模式具有不同的21(,0)值，频率为0的 模式阈值最低，表示为 n ( )
t 0
21l
（二）阈值增益系数
激光自激振荡时，小信号增益系数满足
g ( ) g t
0

l
• 不同纵模具有相同的，因而具有相同的阈 值gt。
V为工作物质的体积， p为泵浦光频率
Ppt
h p n2tV
F s

h p V
F s 21 ( , 0 )l
2、三能级激光器的阈值泵浦功率
参与激光作用的下能级是基态，有
n nt n2t 2
n2 n1 nt n2 n1 n

激光原理第四章

激光原理第四章

激光原理与技术
4.3输出功率与能量
一、连续或长脉冲激光器的输出功率 如果一个激光器的小信号增益系数恰好等于 阈值，激光输出是非常微弱的。实际的激光器 总是工作在阈值水平以上，腔内光强不断增加。 那么，光强是否会无限增加呢?实验表明．在 一定的激发速率下，即当g0(v)一定时，激光器 的输出功率保持恒定，当外界激发作用增强时， 输出功率随之上升，但在一个新的水平上保持 恒定。
hvP nV hvP V t EPt 1 1 21l
激光原理与技术
三能级系统须吸收的光泵能量的阈值为
EPt
hvP nV 21
对于脉冲宽度t0可与相比拟的情况，泵浦能量 的阈值不能用一个简单的解析式表示。但可以 用数字计算的办法求出EPt的值。实验说明，当 固体激光器的氖灯储能电容越大因而光泵脉冲 持续时间t0增长时，光泵的阈值能量也增大。这 是由于t0越长自发辐射的损耗越严重所致。
假设光束直径沿腔长均匀分布，则上式可 化简为
dNl f2 l Nl L' (n2 ) 21 (v, v0 )cNl , Rl dt f1 L ' Rl c
dN l 当 0 dt
0
腔内辐射场由起始的微弱的自 发辐射场增长为足够强的受激 辐射场。
n nt 21 (v, v0 )l
A21 (t t0 ) 2
结论：当t＝t0时,n2(t)达到最大值,当t>t0时,因 自发辐射而指数衰减。 1W13n t0 2 ( 2 1/( A21 S21 )), n2 (t ) A21 1W13
2
在整个激励持续期间n2(t)处在不断增长的非稳 定状态
激光原理与技术
如不采取特殊措施，以均匀加宽为主的固体 激光器一般为多纵模振荡。在含光陷离器的 环形行波腔内，光强沿轴向均匀分布，因而 消除了空间烧孔，可以得到单纵模振荡

北交大激光原理 第4章 高斯光束部分

北交大激光原理 第4章 高斯光束部分
第
一、
学习要求
1．掌握高斯光束的描述参数以及传输特性；
2．理解q参数的引入，掌握q参数的ABCD定律；
3．掌握薄透镜对高斯光束的变换；
4．了解高斯光束的自再现变换，及其对球面腔稳定条件的推导；
5．理解高斯光束的聚焦和准直条件；
6．了解谐振腔的模式匹配方法。
重点
1.高斯光束的传输特性；
2.q参数的引入；
让实部和虚部对应相等得到：
进而得到：
将 代入上式可求出
2.二氧化碳激光器，采用平凹腔，凹面镜的曲率半径 ，腔长 。求出它所产生的高斯光束的光腰大小和位置，共焦参数 及发散角 。
解：
由 ，可得
由 ，可得
3.某高斯光束光腰大小为 ，波长 。求与腰相距30 ，10 ，1 处光斑的大小及波前曲率半径。
解答：
9. 某高斯光束的 ， ，今用一望远镜将其准直，如图3.4所示，主镜用镀金全反射镜： ，口径为 ；副镜为一锗透镜： ，口径为 ，高斯光束的束腰与副镜相距 ，求以下两种情况望远镜系统对高斯光束的准直倍率：（1）两镜的焦点重合；（2）从副镜出射的光腰刚好落在主镜的焦平面。
3.q参数的ABCD定律；
4.薄透镜对高斯光束的变换；
5.高斯光束的聚焦和准直条件；
6.谐振腔的模式匹配方法。
难点
1.q参数，及其ABCD定律；
2.薄透镜对高斯光束的变换；
3.谐振腔的模式匹配。
二、知识点总结
三、典型问题的分析思路
此类问题只涉及高斯光束在自由空间传输，不通过其它光学系统。解此类问题比较简单，根据已知特征参数，高斯光束的结构完全确定，就可以知道任意位置处的光斑尺寸、等相位面曲率半径、q参数及发散角等。
23、试由自在现变换的定义式（2.12.2）用 参数法来推导出自在现变换条件式（2.12.3）。

激光原理第四章习题解答

激光原理第四章习题解答

1 静止氖原子的4223P S →谱线中心波长为632.8纳米，设氖原子分别以0.1C 、O.4C 、O.8C 的速度向着观察者运动，问其表观中心波长分别变为多少？ 解答：根据公式（激光原理P136） 由以上两个式子联立可得：代入不同速度，分别得到表观中心波长为：nm C 4.5721.0=λ，nm C 26.4144.0=λ，nm C 9.2109.0=λ解答完毕（验证过）2 设有一台麦克尔逊干涉仪，其光源波长为λ，试用多普勒原理证明，当可动反射镜移动距离L 时，接收屏上的干涉光强周期性的变化L 2次。

证明：对于迈氏干涉仪的两个臂对应两个光路，其中一个光路上的镜是不变的，因此在这个光路中不存在多普勒效应，另一个光路的镜是以速度υ移动，存在多普勒效应。

在经过两个光路返回到半透镜后，这两路光分别保持本来频率和多普勒效应后的频率被观察者观察到（从半透境到观察者两个频率都不变），观察者感受的是光强的变化，光强和振幅有关。

以上是分析内容，具体解答如下：无多普勒效应的光场：()t E E ⋅=πνν2cos 0 产生多普勒效应光场：()t E E ⋅=''02cos ''πνν在产生多普勒效应的光路中，光从半透经到动镜产生一次多普勒效应，从动镜回到半透镜又产生一次多普勒效应（是在第一次多普勒效应的基础上） 第一次多普勒效应：⎪⎭⎫⎝⎛+=c υνν1'第二次多普勒效应：⎪⎭⎫⎝⎛+≈⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=c c c υνυνυνν21112'''在观察者处：()⎪⎭⎫ ⎝⎛⋅⋅⎪⎭⎫ ⎝⎛⋅+⋅==⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛++⋅=+=t c t c t E t c t E E E E πνυπνυπνυπνπν2cos 22cos 2212cos 2cos 0021观察者感受到的光强：⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⋅⎪⎭⎫ ⎝⎛⋅+=t c I I υνπ22cos 12显然，光强是以频率cυν⋅2为频率周期变化的。

激光原理教案第4章

激光原理教案第4章

激光原理技术及应用》讲义（第4 章高斯光束）王菲长春理工大学2007 年 4 月第四章 高 斯 光 束（4 学时）§1.高斯光束的基本性质、波动方程的基模解在标量近似下稳态传播的电磁场满足赫姆霍茨方程轴的距离 r x 2 y 2呈高斯变化，在近轴处是球面。

4-1-4 )4-1-5)4-1-7a)=>4-1-6) ( 4-1-7a)4-1-7b)( 4-1-8 )Z 0为输入与输出面间距离。

（ 4-1-8 ）4-1-5)=>其中标量 u 0 表示相干光的场分量。

缓变振幅近似下的特是Z 的缓变函数。

将（ 4-1-3）代入（ 4-1-1）得设解参数 P （z ）是与光束传播有关的复相移， q （z ）是复曲率半径， （4-1-1）（ 4-1-2 ） （ 4-1-3 ）（4-1-4）（ 4-1-5 ）表示光束强度随4-1-9)振幅 r 下降到中心值的 1/e 时，光斑尺寸 r 2z 0 = 0，即（4-1-10）k( 4-1-11) 4-1-12)4-1-21）是波动方程（ 4-1-1 ）的一特解，称基模高斯光束。

基模高斯光束的性质由三参数决定。

4-1-22)、高斯光束的基本性质4-1-12) ( 4-1-5) =>4-1-14)(4-1-10)=> 4-1-13)=>4-1-13 ) 由（ 4-1-7b ） 4-1-8) => => 4-1-11)4-1-17)=>4-1-14)4-1-15) (4-1-16) (4-1-17) 4-1-18)4-1-19)=>4-1-20)综上知4-1-21)1.高斯光束在 z ＝常数的平面内，场振幅以高斯函数 exp （ r 2（2z ））的形式从中心 （即传播轴线 ）向外平滑地减小。

当振幅减小到中心值的 l/e 处的 r 值定义为光班半径。

光斑半径随坐标 z 按双曲线规律向外扩展。

2．高斯光束的等相面等相面是指相位相同点的轨迹，一般为空间曲面。

激光原理第四章答案1

激光原理第四章答案1

第四章 电磁场与物质的共振相互作用1 静止氖原子的4223P S →谱线中心波长为632.8nm ，设氖原子分别以0.1c 、0.4c 、0.8c 的速度向着观察者运动，问其表观中心波长分别变为多少？解：根据公式νν=c λν=可得：λλ=代入不同速度，分别得到表观中心波长为： nm C 4.5721.0=λ，0.4414.3C nm λ=，nm C 9.2109.0=λ2．设有一台迈克尔逊干涉仪，其光源波长为λ。

试用多普勒原理证明，当可动反射镜移动距离L 时，接收屏上的干涉光强周期地变化2/L λ次。

证明：如右图所示，光源S 发出频率为ν的光，从M 上反射的光为I '，它被1M 反射并且透过M ，由图中的I 所标记；透过M 的光记为II '，它被2M 反射后又被M 反射，此光记为II 。

由于M 和1M 均为固定镜，所以I 光的频率不变，仍为ν。

将2M 看作光接收器，由于它以速度v 运动，故它感受到的光的频率为：因为2M 反射II '光，所以它又相当于光发射器，其运动速度为v 时，发出的光的频率为这样，I 光的频率为ν，II 光的频率为(12/)v c ν+。

在屏P 上面，I 光和II 光的广场可以分别表示为：S2M (1)vcνν'=+2(1)(1)(12)v v v c c cνννν'''=+=+≈+00cos(2)cos 2(12)I II E E t v E E t πνπν=⎡⎤=+因而光屏P 上的总光场为光强正比于电场振幅的平方，所以P 上面的光强为它是t 的周期函数，单位时间内的变化次数为由上式可得在dt 时间内屏上光强亮暗变化的次数为(2/)mdt c dL ν=因为dt 是镜2M 移动dL 长度所花费的时间，所以mdt 也就是镜2M 移动dL 过程中屏上光强的明暗变化的次数。

对上式两边积分，即可以得到镜2M 移动L 距离时，屏上面光强周期性变化的次数S式中1t 和2t 分别为镜2M 开始移动的时刻和停止移动的时刻；1L 和2L 为与1t 和2t 相对应的2M 镜的空间坐标，并且有21L L L -=。

激光原理与技术(第四章2)

激光原理与技术(第四章2)
四能级系统速率方程
1）单模振荡（第 l 个模，模频率为n)
E3 E2
w03 A30 S30
与三能级相比，激光下能级E1不再
S32 S21 A21 W21 W12 S10
是基态能级, 在热平衡状态下，处于 E1的粒子数很少,很容易建立粒子数 反转。 四能级系统，一般有
E1
E0
参与产生激光的有四个能级:基 态能级E0(抽运过程的低能级)、 抽运高能级E3、激光上能级
dNl N n2W21 n1W12 l dt Rl f2 Nl ) n n n , n vN 0 l 2 f 1 21 Rl 1
I 1 I 0 e I t ) I 0 e I 0e
t L c t
只考虑损耗
dN f2 N n2 n1 21vN dt f1 R
E3E2无辐射跃 迁量子效率 (泵浦效率) n2 A21 S21 )
E2E1 荧光量子效率
N--各模式光子数密度总和
n0 n1 n2 n3 n
总量子效率 F 12
N l hn
dNl Nl n2W21 n1W12 dt Rl
n0 n1 n2 n3 n
A21 ~ g n ,n 0 )N l nn
21 n ,n 0 )N l v （4.4.13）
为何没有包括A21引起的光子数？
式中忽略了n3 W30项，因为n3很小,故n3W30<<n0W03
I= Nhnv dz=vdt
dz
I= Nhnv
dI g Idz
dz=vdt
I I 0e
g z
0
dI n 21 n ,n 0 )vNhndz

大学课件-激光原理_第四章

大学课件-激光原理_第四章

I I 0e gz
2 2 2 d ne 0 d 4 0 m0 2 2 2 0
2
正常色散
0
反常色散
-1

将上述结果推广到普遍的状态，令Δn代替(-n)，并令ΔH=/2
H ne 2 g 2 4 0 mc 2 H 0 2
2
ne2 0 1 1 2 2 2 16 m 2 0 0 H 0 2
E ( z, t ) E0e
i

c
z
i 1
e z it t c z 2 E ( z, t ) E0e c e z c I I 0e 2 I E (t )
第四章 电磁场和物质的共振相互作用
§4-1 光和物质相互作用的经典理论简介 §4-2 谱线加宽和线型函数 §4-3 典型激光器速率方程 §4-4 均匀加宽物质的增益系数 §4-5 非均匀加宽物质的增益系数 §4-6 综合加宽物质的增益系数
§4-1 光与物质相互作用的经典理论简介
一、原子自发辐射的经典模型
根据不同的近似基本上可以分为四类： 一、经典理论(经典原子发光模型)
出发点是：将原子系统和电磁场都作经典处理，即用经典 电动力学的麦克斯韦方程组描述电磁场 ,将原子中的运动电子 视为服从经典力学的振子。 成功地解释了物质对光的吸收和色散现象,定性地说明了原 子的自发辐射及其谱线宽度,等等。
此外，经典理论在描述光和物质的非共振相互作用时也起 一定作用。
2 x x 0 x 0

激光原理教案第四章

激光原理教案第四章

hvP nV hvP V t EPt 1 1 21l
激光原理与技术
三能级系统须吸收的光泵能量的阈值为
EPtΒιβλιοθήκη hvP nV 21对于脉冲宽度t0可与相比拟的情况，泵浦能量的阈 值不能用一个简单的解析式表示。但可以用数字计 算的办法求出EPt的值。实验说明，当固体激光器的 氖灯储能电容越大因而光泵脉冲持续时间t0增长时， 光泵的阈值能量也增大。这是由于t0越长自发辐射 的损耗越严重所致。
hvP nV 2 F s
四、短脉冲激光器的阈值泵浦能量 若光泵激励时间很短，则在激励持续期间E2能级的 自发辐射和无辐射跃迁的影响可以忽略不计。在这种 情况下，要使E2能级增加一个粒子，只须吸收1／1 个泵浦光子。因此，当单位体积中吸收的泵浦光子数 大于n2t／1时，就能产生激光。由此可见，四能级系 统须吸收的光泵能量的阈值为
激光原理与技术
4.2 激光器的振荡模式
一、均匀加宽激光器中的模竞争
1．增益曲线均匀饱和引起的自选模作用
图4.2.1 均匀加宽激光器中建立稳态振荡过程中的模竞争
激光原理与技术
图4.2.2 说明空间烧孔效应的图
激光原理与技术
g(vq1, Ivq1 , Ivq , Ivq1 ) gt , g(vq1, Ivq1 , Ivq , Ivq1 ) gt
激光原理与技术
PPt
hvP ntV
F s

F 21 s l
hvP V
2.三能级激光器
n2t
n nt 2
在典型三能级系统红宝石中
17 3
n 1.9 10 cm
19
3
n nt 8.7 10 cm , nt n, n2t 2

激光原理-第四章 半导体激光器

激光原理-第四章 半导体激光器

第二节 激发与复合辐射

若掺杂原子比材料原子少一个电子,则附加能级接近 价带,其上的空穴很容易进入价带,使价带中出现大量 过剩空穴,这种材料称为p型材料,而杂质称为受主。
掺杂的净效果是在导带和价带中形成过剩的自由载流 子。 P掺杂三价元素（杂质），载流子主要是空穴，而杂 质称为受主 N掺杂5价元素（杂质），载流子主要是电子,而杂质 称为施主 p型材料和n型材料接触时形成pn结,

式中,kpn 为声子波矢,k pn 一般比k小1个量级左右。
初态与末态相应于k空间不同点的电子跃迁称为非 竖直跃迁或间接跃迁。在这种跃迁中,发射或吸收一 个光子的同时,必须伴随发射或吸收一个适当波数的 声子,以满足动量守恒,因而属于二级过程。其几率比 属于一级过程的纯光跃迁小得多,故不适合用于激光 发射。
E
导带 Eg
满带
半导体的能带
第一节半导体的能带结构和电子状态
二、半导体中的电子状态 用量子力学确定孤立原子的电子能量和运动状态是通过求解薛定 鄂方程实现的。然而,由于固体中所含原子数量极大,对每个电 子求解薛定鄂方程是根本不可能, 只能采取某种近似的方法:
其相应的能量本征值为
h2k 2 E V 2me
1．满带（排满电子）(价带) 2．价带（价电子能级分离后形成的能带,能带中一部分能级排 满电子） 3. 导带 （未排满电子的价带） 3．空带（未排电子） 空带也是导带 4．禁带（不能排电子）
第一节半导体的能带结构和电子状态




半导体材料Si和Ge为例,每个原子有4个价电子,在原子状态中s态 和p态各2个。 由轨道杂化重新组合的两个能带中各含２Ｎ 各状态，较低的一 个正好容纳４Ｎ 个价电子， 所有的电子排满了s轨道,只有当能带被电子部分填充时,外电场 才能使电子的运动状态发生改变而产生导电性。 这些材料低温下不导电,在温度较高时,部分电子从价带激发到导 带,表现出导电性。

激光原理高斯光束

激光原理高斯光束
NJUPT
高斯光束的基本性质
振幅分布及光斑半径
A(r)
A0
A0 e
0 r =ω(z) r
ω(z) =ω0
1+
z f
2
=ω0
λz 2
1
+
πω02
P67
=f π= ω02 1 L 共焦腔反射镜的焦距 λ2
NJUPT
高斯光束的基本性质
振幅分布及光斑半径
ω(z)
F
ω0
z
−ω0
F
ω(z) 随z以双曲线函数变化
)
−
ϕ
(
z
)
u00( x= , y, z)
c ω 0 exp ω (z)
{−ik z +
x2 + 2
y2 1 (− R(z)
iλ kω 2(
z
)
)
+
iϕ
(z)
q( z )复曲率半径
1
1
iλ
= q(z)
R(z) − πω 2 (z)
NJUPT
高斯光束的 q 参数（复曲率半径）
u00 ( x, = y, z)
腰斑放大率：=k ω=0′ ω0
1
<1
1+
f F
2
F
1
+
F f
2
<
F
NJUPT
高斯光束的聚焦
F 一定时，ω0′与 l′ 随 l 的变化情况 （1） l < F 结论
l = 0 时，ω0′ < ω0
不论透镜焦距 F 为多大，都有一定 的聚焦作用；
F越小，聚焦作用越好；
像方腰斑的位置处在透镜后焦点以内。

激光原理第四章

激光原理第四章

n1W14 n 4S43
n 4S43 n 3 A 32 n 2S21 n1W14
n1+n3=n
n n3
0
→
W14 n
n1+n3=n
W14 A32
小信号增益系数
定义
G dI(z) I( z)dz
计算
G
1 l
ln
I I0
I0:初光强，I:末光强, l:传播距离
孔宽

1
0
I 1 Is
H
)
增益曲线均匀下降
孔深 增益曲线烧孔
Gi ( 1 ) Gt
二、非均匀加宽
1、对入射强光 ( 1 , I ) 的增益系数
1
Gi ( ν 1 , I 1 )
G ( 1)
0 i

Gm 1 I 1 Is

4 ln 2 ( 1 0 ) i
2
2
e
1
I 1 Is
各增益系数
均匀加宽
G ( ν)
0
非均匀加宽
Gm 2
4 ln 2( 0 ) i
4 i
大信号反转粒子数
一、均匀加宽
1、反转粒子数表达式
n( ν1 , I 1 ) ( ν1 ν 0 )
2

2 2
νH 2
( ν1 ν 0 )
2
(1
νH 2
I 1 Is
n )
0
Is
4 ν0 h H
2 3
v
2
的强光入射时的 大信号反转粒子数 ，Is:饱和光强参数(w/mm2)
(1)光源静止、接收器运动

激光原理与技术--第四章 激光的基本技术

激光原理与技术--第四章 激光的基本技术

由四边形ABCD知 T+2 α+(180- Φ)=360
由四边形ABCO知 β+T=1800
上两式联立得: α= (Φ + β)/2,所以 (由折射定律，见上面公式）
nsin 2()/sin 2
2arcnssiin 2n ) (
式中,α为入射角,n为析射率；β为棱镜的顶角；Φ为偏向
角。定义棱镜的角色散率为
4.1.1 激光单纵模的选取
1. 均匀增宽型谱线的纵模竞争
(1) 当强度很大的光通过均匀增益型介质时粒子数反转分布值下降，增 益系数相应下降，但光谱的线型并不改变。
(2) 多纵模的情况下，如图4-1所示，设有q-1，q，q+1三个纵模满足振 荡条件。随着腔内光强逐步增强，q-1和q+1模都被抑制掉，只有q模的 光强继续增长，最后变为曲线3的情形。
d (sa 1 i n sia 2 n ) m式求出： d (0coa2sd2a)md D d2a m sia n1sia n2
d dcoa2s coa2s 通常光栅工作在自准直状态下，即α1= α2= α (α为光栅的闪耀角，即光栅平面 的法线Ｎ0 与每条缝的平面的法线N2之间的夹角，对小斜面而言是正入射），
环形行波腔激光器示意图
4.1.2 激光单横模的选取 1. 衍射损耗和菲涅耳数 (1) 由于衍射效应形成的光能量损失称为衍射损耗。 (2)如图4-4所示的球面共焦腔，镜面上的基横 模高斯光束光强分布可以表示为
0 I()2 d I00 ex 2 p 1 2 2)d (2 2 I0 1 2
Δν=c/[2(l1-l2)]
1i 2 j
Δν=c/[2(l1-l2)] 适当选择l1及l2，可以使复合腔的频率间隔足够大，即两 相邻纵模间隔足够大，与增益线宽相比拟时，即可实现 单纵模运转。

北交大激光原理-第4章-谐振腔部分

北交大激光原理-第4章-谐振腔部分
——等相位面与共焦腔镜面重合。
——等相位面为平面
(共焦腔基模光束)远场发散角： [弧度]
5．一般稳定球面腔问题
可以借助于其等价共焦腔行波场的解析解的特性表达出来，此处可参考教科书。
6．非稳定谐振腔问题
关于非稳定谐振腔的问题主要包括求出共轭像点 和 的位置；计算非稳腔的能量损耗率、几何放大率等。
共轭像点 和 的位置分别为 ，由球面镜成像公式
而对于环形腔和折叠腔〔非共轴球面腔〕，由于象散，球面镜在子午面和弧矢面的焦距不共点。其中子午面为环形回路所在平面，弧矢面为包含回路一边长，垂直于子午面的平面。对于在由光轴组成的平面内传输的子午光线， 。对于在与此垂直的平面内传输的弧矢光线， ， 为光轴学谐振腔积分方程的特征值 ，它的实部决定腔损耗，特征值 的虚部决定光波的单程相移。将特征值代入 中得： 。即 表示腔内经单程度越后自再现模的振幅衰减。即 的实部决定腔损耗， 表示每经一次度越的相位滞后，所以 的虚部决定的单程相移。
14.如下列图所示三镜环形腔，已知l，试画出其等效透镜序列图，并求球面镜的曲率半径R在什么范围内该腔是稳定腔。图示环形腔为非共轴球面镜腔，在这种情况下，对于在由光轴组成的平面内传输的子午光线，f =Rcos/2，对于在于此垂直的平面内传输的弧矢光线，f =R/(2cos)，为光轴与球面镜法线的夹角。
解得：
几何放大率
镜 的单程放大率
镜 的单程放大率
非稳腔对几何自再现波型在腔内往返一周的放大率
对望远镜非稳定腔〔实共焦腔和虚共焦腔〕
平均单程能量损耗
往返能量损耗
四、思考题
1.光学谐振腔的作用是什么？
2.光学谐振腔的构成要素有哪些，各自有哪些作用？
3.光学谐振腔有哪些常用研究方法？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 2 2 2 umn x, y, z Cmn H m x H n 1 2 ws 1 2 ws 2 x2 y2 exp 1 2 w2 exp i x, y, z s y
m、n分别为沿镜面极坐标系的径向暗 环数和角向暗直径数（不含中心点）
(2) 本征值σmn和单程衍射损耗、单程相移 损耗主要指衍射损耗。对于一次渡越的衍射损耗（单程衍射 损耗）用δ表示。定义为

uq uq 1 uq
2
2
2
uq1 uq
功率损耗
2 mn 1 mn
积分方程的核 umn为本征函数 ，σmn 为本征值
mn umn ( x, y ) K ( x, y, x' , y ' )umn ( x' , y ' )ds'
umn和σmn的下标表示该方程存在一系列的不连续的本征函数解与本征 值解，说明在某一给定开腔中，可以存在许多不同的自再现模
积分方程解的物理意义
例题
1、He-Ne激光器的中心波长是6328Å，其线宽是Δvf＝ 1.5×109Hz，试计算腔长分别为L1 =10 cm 以及L2 =30 cm时， 激光腔内可能存在的最多纵模数？
vq
c 2L
＝ .5 109 Hz, 0.5 109 Hz 1
L=10cm, n=2 L=30cm, n=3
单程衍射损耗:
衍射损耗定义： mn 1 mn
2
mn e
i[ kL( mn1) ] 2

mn 0
单程附加相移与谐振频率:
一般忽略不计
单程附加相移： mn kL arg mn (m n 1) 谐振频率： νmnq

2
qc c mn 2L 2L
c 3 108 L 0.2 m 9 μΔν 1.5 10
腔长最长不得大于 0.2m
4、横模和纵模之间的联系
横模：谐振腔所允许的光场的各种横向稳定分布 纵模：谐振腔内沿纵向（光的传播方向）不同的稳定的光场分布
纵模和横模各从一个侧面反 映谐振腔内稳定的光场分布。 只有同时用纵模和横模概念才 能全面反映腔内光场的分布
因 L, R >> a >>λ ，故 cosθ＝1， 又用了L代替ρ(一般不可替换) 自再现模所满足的积分方程：
mn umn ( x, y ) K ( x, y, x' , y ' )umn ( x' , y ' )ds '
其中 : ik ik ( x , y , x ', y ') i ik ( x , y , x ', y ') K ( x, y , x ' , y ' ) e e 2L L
X 2 Y 2 2
mn e
i[ kL( mn1) ] 2

其中： Cmn为与m、n 有关的常量
X x
2 2 , Yy L L
Hm(X ) 和 Hn(Y )均为厄密多项式
本征函数： umn Cmn H m ( X ) H n (Y )e
其中： X x
2 2 ,Y y L L
νm νn νq 2
方形镜共焦腔的振荡频谱
2、共焦腔中的行波场与腔内外的光场分布
1） 求解方法
腔内光场: 驻波分布
由镜面M1、 M2上的场在腔内造成的行波（叠加）形的；基 尔霍夫衍射公式计算； 腔外的光场 腔内沿一个方向传播的行波透过镜面的部分，即行波函数 乘以镜面的透射率t.
2）将镜面场分布代入基尔霍夫衍射公式可得腔内场分布： 选择腔的中心为坐标原点
σmn的模反映自再现模在腔内单程渡越（传输）时所引起的 本征值幅角与自再现模腔内单程渡越后所引起的总相移有关
uq1 uq arg uq1 arg arg uq
自再现模在对称开腔中单程渡越所产生的总相移定义为
arguq1 arguq arg
单程总相移相对于几何相移（由腔长L决定）产生附加相移 Δφ ：
其中q=1, 2, 3….
每个q值对应一个驻波；谐振腔内形成的每一列驻波称为一 个纵模，q为纵模序数
纵模频率
kL
2 2q k 2ν c
（2） 纵模频率间隔
qc c qc νmnq mn 2 L 2L 2 L
一时刻新的波前形状由次级子波的包络面所决定；
菲涅耳干涉概念：子波源所发的波应该是相干的 菲涅尔－基尔霍夫衍射公式：基尔霍夫进一步利用格林函数法
求解波动方程，得到原理的数学表达式
ρ
ik u ( P) 4
u' (P)

eik

(1 cos )ds'
2、光学谐振腔的自再现模积分方程
ws xs2 ys2 L
位相分布: umn Cmn Fm ( X ) Fn (Y )
Fm ( X ) H m ( X )e X
2
2
, Fn (Y ) H n (Y )e Y
2
2
由于umn(x, y) 为实函数，所以共焦腔反射镜面的光场是一个等相位 面 (无论是基模，还是高阶模)

X 2 Y 2 2
Cmn为与m、n 有关的常量
Hm(X)和Hn(Y)均为厄密多项式： H 0 ( X ) 1
H1 ( X ) 2 X
参考书： 《激光原理》周炳琨主编 国防工业出版社 《激光物理学》邹英华、孙陶亨编，北京大学出版社
H2 ( X ) 4X 2 2 2 dm X 2 H m ( X ) (1) m e X e m dX
(1) 本征函数umn和激光横模
本征函数umn: 表示在激光谐振腔中存在的稳定的横向场分布，就 是自再现模，通常叫做“横模”，m、n称为横模序数。 umn的模：对称开腔任一镜面上的光场振幅分布，
umn的幅角：代表镜面上光场的相位分布
方形镜共焦腔模式花样（轴对称）
圆形镜共焦腔模式花样（旋转对称）
*
m、n分别为横截面上x、y方向出 现的节点（场强为零的位置）数
问题：如果已知某一镜面上的场分布，如何求解出在衍射作
用下经腔内一次渡越（传播）而在另一个镜面上生成的场？
菲涅耳－基尔霍夫衍射公式:
可以给出空间某一点（或某一表面）上的场与处于有限距离 上的另一个表面上场的关联。
1、菲涅耳--基尔霍夫衍射公式
为惠更斯-菲涅耳原理的数学表达式
惠更斯子波概念：波面上每一点可看作次球面子波的波源，下
可得：
去掉下标：
u ( x' , y ' )
q M'
e ik

(1 cos )ds'
ik u q ( x, y) 4
u
q
( x' , y ' )
e ik
ik u( x, y) 4
u( x' , y' )
e ikBiblioteka (1 cos )ds'

(1 cos )ds'
《激光原理与技术》
第4章 激光器的输出特性
目录
1 4.1 光学谐振腔的衍射理论
2
3 4 4 2
4.2
4.3 4.4 4.5 4.6
对称共焦腔内外的光场分布
高斯光束的传播特性 稳定球面腔的光束传播特性 激光器的输出功率 激光器的线宽极限
1
4.7 激光光束质量的品质因子M2
4.1
光学谐振腔的衍射理论
书中有误
2） 镜面上自再现模场的特征
本征函数： umn Cmn H m ( X ) H n (Y )e
X 2 Y 2 2
振幅分布:
则有
令 Fm ( X ) H m ( X )e
umn Cmn Fm ( X ) Fn (Y )
X 2 2
,
Fn (Y ) H n (Y )e
Y 2 2
不同的纵模和不同横模都有各 自对应不同的光场分布和频率。
同一q值下不同横模表现
4.2
对称共焦腔内外的光场分布
对称共焦腔：由两个曲率半径相等的凹球面镜构成，它们
的焦点重合并在曲率中心连线上
对称共焦腔 以方形镜面的对称共焦腔为例，求解积分方程，获得 共焦腔镜面上的场分布 共焦腔中行波场与腔内外的场分布
将衍射积分公式运用到光学谐振腔
由M’上的光场分布可以计算出M上 的场分布函数
假设uq ( x’, y’ ) 为经过 q 次传播后在 M’上形成的场分布， uq+1( x, y ) 为经过 q+1次渡越到达 M 所形成的场分布， 则uq+1与uq之间应满足如下的迭代关系：
ik uq 1 ( x, y) 4
2 2 I mn umn Fm ( X )Fn2 (Y )
Fm(X) ~X 及 Fn(Y) ~Y 的
变化曲线及
相应的光强 分布
特例：基横模 TEM00
TEM00 的场分布： u00 C00e
x2 y 2 L
u00max= C00 , 位置：镜面中心
当 x2+y2 =λL /π, u00=C00 /e 定义：镜面上光斑有效截面半径
讨论激光器中所用的开腔式谐振腔（没有侧面边界的腔）
问题： 开腔中是否存在不随时间而变化的稳定电磁场分布即是否存 在电场场的本征态？应该如何求出这些场分布？
几何光学 波动光学 讨论谐振腔振荡模式、光束结构及传输特性、衍射损耗等， 该理论建立在模式再现概念及惠更斯-基尔霍夫衍射积分公 式基础上。