第1课时 仰角与俯角问题
- 格式:ppt
- 大小:4.53 MB
- 文档页数:143

解直角三角形的应用-仰角俯角问题能量储备仰角、俯角:如图2446(1)所示,在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角。
通关宝典★ 基础方法点方法点:解直角三角形在实际问题中的应用中正确选取直角三角形的边角关系是求解的关键。
例1:如图24410所示,某电视塔高AB 为610米,远处有一栋大楼,某人在楼底C 处测得塔顶B 的仰角为45°,在楼顶D 处测得塔顶B 的仰角为39°。
(1)求大楼与电视塔之间的距离AC ;(2)求大楼的高度CD (精确到1米)。
解:(1)在△ABC 中,∵ ∠ACB =45°,∠A =90°,∴ AC =AB =610米。
答:大楼与电视塔之间的距离AC 为610米。
(2)由矩形的性质可知DE =AC =610米。
在Rt △BDE 中,由tan ∠BDE =BE DE,得BE =DE·tan 39°。
又∵CD =AE ,∴CD =AB -DE·tan 39°=610-610×tan 39°≈116(米)。
答:大楼的高度CD 约为116米。
例2:如图24428所示,为了测得电视塔的高度AB ,在D 处用高为1.2米的测角仪CD ,测得电视塔顶端A 的仰角为42°,再向电视塔方向前进120米,又测得电视塔顶端A 的仰角为61°.求这个电视塔的高度AB .(精确到1米)解:如图24429所示,设AE 为x 米,则塔的高度为(x +1.2)米.∵ tan 61°=AE EF =x EF ,∴ EF =x tan 61°. 又∵ tan 42°=AE CE ,∴ CE =x tan 42°. ∵ CE =120+x tan 61°, ∴ x tan 42°=120+x tan 61°, 解得x ≈215.7,∴ x +1.2≈217(米).∴ 这个电视塔的高度AB 约为217米。

4.4解直角三角形的应用
第1课时仰角、俯角相关问题
活动四:课堂总结反思【当堂训练】
1.教材P126练习中的T1,T
2.
2.教材P129习题4.4中的T3,T4,T5.
当堂检测,及
时反应学习效果.
【知识网络】
提纲挈领,重点
突出.
【教学反思】
①[授课流程反思]
本课时在新课引入时以学生熟悉的校园生活为背景,提
出了本节课要用到的仰角、俯角,并对这两种角进展了简单
的描绘,学生应用时应该是水到渠成的.
②[讲授效果反思]
应用仰角、俯角解决解直角三角形中的问题是本节课的
重点,所以本节课选择了3个探究问题,比拟根底,希望师
生共同理解仰角、俯角的初步应用,接着又选择了4个中考
题作为例题讲解,建议每道例题学生先做,然后老师再用多
媒体展示答案,突出学生的主体地位和老师的主导作用.
③[师生互动反思]
___________________________________________
___________________________________________
④[习题反思]
好题题号_____________________________________
错题题号____________________________________
反思,更进一步提
升.。



仰角与俯角-北京版九年级数学上册教案一、教学目标1.理解仰角和俯角的概念;2.掌握仰角和俯角的计算方法;3.熟练掌握仰角和俯角在问题中的应用。
二、教学重难点1.仰角和俯角的概念理解;2.仰角和俯角的计算方法;3.问题解决中的应用。
三、教学内容1.仰角和俯角的概念1.仰角:指从水平面向上看的角度,介于0度和90度之间。
2.俯角:指从水平面向下看的角度,介于0度和90度之间。
2.仰角和俯角的计算方法1.仰角的计算方法:tanθ=h/d,其中h表示所在位置到眼睛的高度,d表示所在位置到眼睛的水平距离。
2.俯角的计算方法:tanθ=h/d,其中h表示所在位置到眼睛的高度,d表示眼睛到所在位置的水平距离。
3.仰角和俯角在问题中的应用1.如何在地图上计算山顶的高度?2.如何在地图上计算建筑物的高度?3.如何计算人的视线高度?四、教学方法1.教师授课;2.学生自主学习和合作学习;3.组织小组讨论和分享。
五、教学步骤1.引入仰角和俯角的概念;2.讲解仰角和俯角的计算方法;3.演示仰角和俯角在问题中的应用,组织学生分组讨论和分享;4.组织学生进行练习和方法探究;5.总结巩固本节课的知识点。
六、教学评估1.配置测试题:给出图像及相关数据,要求学生计算对应的仰角和俯角;2.引导学生完成解决实际问题的探究作业;3.鼓励学生自主扩展阅读。
七、教学反思通过此次教学,帮助学生掌握仰角和俯角的概念,以及计算方法。
同时,引导学生在实际问题中发现角度计算的应用。
未来的教学中,可以通过更多的案例和实例来加强学生的应用能力,同时加强学生自主探究和合作学习的能力。

4.4 解直角三角形的应用第1课时 仰角、俯角问题一.教学三维目标(一)、知识目标使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.(二)、能力目标逐步培养分析问题、解决问题的能力.二、教学重点、难点和疑点1.重点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.2.难点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.三、教学过程(一)回忆知识1.解直角三角形指什么?2.解直角三角形主要依据什么?(1)勾股定理:a 2+b 2=c 2(2)锐角之间的关系:∠A+∠B=90°(3)边角之间的关系:tanA=的邻边的对边A A ∠∠(二)新授概念 1.仰角、俯角当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.教学时,可以让学生仰视灯或俯视桌面以体会仰角与俯角的意义.2.例1:如图(6-16),某飞机于空中A 处探测到目标C ,此时飞行高度斜边的邻边A A ∠=cos 斜边的对边A A ∠=sinAC=1200米,从飞机上看地平面控制点B 的俯角α=16°31′,求飞机A 到控制点B 距离(精确到1米)解:在Rt △ABC 中sinB=AB AC∴AB=B AC sin =2843.01200=4221(米)答:飞机A 到控制点B 的距离约为4221米.例2:2003年10月15日“神州”5号载人航天飞船发射成功。
当飞船完成变轨后,就在离地形表面350km 的圆形轨道上运行。
如图,当飞船运行到地球表面上P 点的正上方时,从飞船上能直接看到地球上最远的点在什么位置?这样的最远点与P 点的距离是多少?(地球半径约为6400km ,结果精确到0.1km )分析:从飞船上能看到的地球上最远的点,应是视线与地球相切时的切点。
将问题放到直角三角形FOQ 中解决。

解直角三角形的仰角俯角问题
仰角和俯角是解直角三角形问题中常见的概念。
在直角三角形中,仰角是锐角的补角,而俯角是锐角的余角。
1.仰角:在直角三角形中,与直角的锐角相邻的角叫做仰角。
仰角是锐角的
补角,即仰角= 90° - 锐角。
2.俯角:与直角的锐角相对的角叫做俯角。
俯角是锐角的余角,即俯角= 锐
角。
解这类问题时,通常需要利用三角函数的性质和关系,如正切、正弦、余弦等,以及直角三角形的边和角的关系,如勾股定理等。
以下是一个简单的例子:
题目:一个塔的高度是30米,从塔顶测得某建筑物顶部的仰角为24°,从地面测得该建筑物顶部的俯角为66°,求这个建筑物的高度。
解:设建筑物的高度为h 米。
根据三角函数的性质和关系,我们有:
塔顶到建筑物顶部的距离= 塔的高度× 正切(仰角) = 30 × tan(24°)。
建筑物顶部到底部的距离= 建筑物的高度× 正切(俯角) = h × tan(66°)。
由于直角三角形中的勾股定理,我们有:
塔顶到建筑物顶部的距离^2 + 建筑物顶部到底部的距离^2 = 塔高度的^2。
代入已知数值,我们可以得到一个关于h 的方程,并解出h 的值。

2017九年级数学上册4.4 第1课时仰角、俯角问题教案1 (新版)湘教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017九年级数学上册4.4 第1课时仰角、俯角问题教案1 (新版)湘教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017九年级数学上册4.4 第1课时仰角、俯角问题教案1 (新版)湘教版的全部内容。
4.4 解直角三角形的应用第1课时仰角、俯角问题1。
巩固解直角三角形相关知识.2.能运用解直角三角形知识解决仰角和俯角的问题.(重点,难点)一、情境导入秋千是我们生活中常见的娱乐器材,如图所示是秋千的简图,秋千拉绳(OA)的长为3m,静止时秋千踏板(B,大小忽略不计)距离地面的距离(BE)为0。
5m,秋千向两边摆动时,若最大的摆角(摆角是指秋千拉绳与铅垂线的夹角∠AOB或∠COB)约为52°。
你能否通过所学知识求出秋千踏板与地面最大距离约为多少?二、合作探究探究点一:仰角、俯角问题【类型一】仰角问题如图所示,为了测量山高AC,在水平面点B处测得山顶A的仰角是( )A.∠AB。
∠ABCC。
∠ABDD。
以上都不对解析:B.方法总结:解此类问题,要弄清仰角的概念,即视线与水平线的夹角.【类型二】俯角问题如图,飞机A在目标B正上方1000m处,飞行员测得地面目标C 的俯角为30°,则地面目标B,C之间的距离是W。
解析:由题意可知,在Rt△ABC 中,∠B=90°,∠C=∠CAD=30°,AB=1000m,∴BC=错误!=错误!=1000错误!(m),故填1000错误!m。
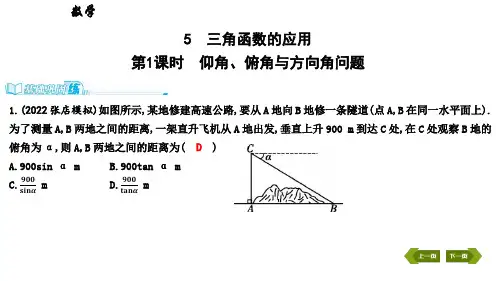

4.4第1课时仰角、俯角相关问题一、选择题1.如图1,某工程队沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,且BD=500米,∠D=55°,为了使点A,C,E 在一条直线上,那么开挖点E与D的距离是()A.500sin55°米B.500cos35°米C.500cos55°米D.500tan55°米图1图22.如图2,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米.2≈1.414)() A.34.14米B.34.1米C.35.7米D.35.74米3.如图3,钓鱼竿AC长6 m,露在水面上的鱼线BC长3 2 m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3 3 m,则鱼竿转过的角度是()A.60° B.45° C.15° D.90°图3图44.如图4,学校环保社成员想测量斜坡CD旁一棵树AB的高度(E,C′,A在同一水平线上),他们先在点C处测得树顶B的仰角为60°,然后在坡顶D处测得树顶B的仰角为30°,已知斜坡CD的长度为20 m,DE的长为10 m,则树AB的高度是()A.20 3 B.30 m C.30 3 m D.40 m二、填空题5.如图5,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为________米.(结果保留根号)图5图66.如图6,为了测量出一垂直于水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角为45°,随后沿直线BC向前走了100米后到达D处,在D处测得顶端A的仰角为30°,则建筑物AB的高度约为________米.(注:测量人员的身高忽略不计,结果按四舍五入保留整数.参考数据:2≈1.41,3≈1.73)三、解答题7.小亮在某桥附近试飞无人机,如图7,为了测量无人机飞行的高度AD,小亮通过操控器指令无人机测得桥头B,C的俯角分别为60°,30°,且D,B,C在同一水平线上.已知桥BC=30米,求无人机飞行的高度AD约为多少.(精确到0.01米.参考数据:2≈1.414,3≈1.732)图78.如图8,小明在教学楼A处分别测得对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一水平面上,观测点距地面的垂直高度AB为15 m,求实验楼的垂直高度即CD的长约为多少.(精确到1 m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)图89.如图9,某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A 距甲楼的距离AB是31 m,在A处测得甲楼顶部E处的仰角是31°.(1)求甲楼的高度BE及彩旗的长度AE(精确到0.01 m);(2)若小颖在甲楼楼底C处测得学校后面医院(乙楼)楼顶G处的仰角为40°,爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°,求乙楼的高度及甲、乙两楼之间的距离(精确到0.01 m).(参考数据:cos31°≈0.857,tan31°≈0.601,cos19°≈0.946,tan19°≈0.344,cos40°≈0.766,tan40°≈0.839)图910.图10是某小区入口实景图,图②是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的点O处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.(1)求点M到地面的距离;(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD 保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:3≈1.732.结果精确到0.01米)图10一题多解在一次科技活动中,小明进行了模拟雷达扫描实验.如图11,△ABC是表盘,其中AB=AC,∠BAC=120°,在点A处有一束红外光线AP,从AB开始,绕点A逆时针匀速旋转,每秒旋转15°,到达AC后立即以相同的旋转速度返回AB,到达后立即重复上述旋转过程.小明通过实验发现,光线从AB处旋转开始计时,旋转1秒,此时光线AP交BC边于点M,BM的长为(20 3-20)cm.(1)求AB的长;(2)从AB处旋转开始计时,若旋转6秒,此时光线AP与BC边的交点在什么位置?若旋转2030秒,交点又在什么位置?请说明理由.图11详解详析[课堂达标]1.[解析] C∵∠ABD=145°,∴∠EBD=35°.∵∠D=55°,∴∠E=90°.在Rt△BED中,BD=500米,∠D=55°,∴ED=500cos55°米.故选C.2.[解析] C过点B作BF⊥CD于点F,过点B′作B′E⊥BD于点E.由题意,得∠DB′F=67.5°,∠DBF=45°,∴∠BDC=45°,∠BDB′=∠B′DC=22.5°,∴B′E=B′F.∵∠EBB′=45°,∠BEB′=90°,∴B′E=B′F=22BB′=10 2米,∴DF=BB′+B′F=(20+10 2)米,∴DC=DF+FC=20+10 2+1.6≈35.7(米).故选C.3.[解析] C在Rt△ACB中,∵sin∠CAB=BCAC=3 26=22,∴∠CAB=45°.在Rt△AC′B′中,∵sin∠C′AB′=B′C′AC=3 36=32,∴∠C′AB′=60°,∴∠CAC′=60°-45°=15°,∴鱼竿转过的角度是15°.故选C.4.[答案] B5.[答案] 100 2[解析] 连接AN.由题意知,BM⊥AA′,BA=BA′,∴AN=A′N,∴∠ANB=∠A′NB=45°.∵∠AMB=22.5°,∴∠MAN=∠ANB-∠AMB=22.5°=∠AMN,∴AN=MN=200米.在Rt△ABN中,∠ANB=45°,∴AB=22AN=100 2(米).故答案为100 2.6.[答案] 137[解析] 设AB =x 米.在Rt △ABC 中,∵∠ACB =45°,∴BC =AB =x 米,则BD = BC +CD =(x +100)米.在Rt △ABD 中,∵∠ADB =30°,∴tan ∠ADB =AB BD =33,即xx +100=33,解得x =50+50 3≈137,即建筑物AB 的高度约为137米.故答案为137. 7.解:由题意,得AE ∥CD ,∴∠ACD =∠EAC =30°,∠ABD =∠EAB =60°. 设AD =x 米.在Rt △ACD 中,tan ∠ACD =ADCD,∴CD =3x 米. 在Rt △ABD 中,tan ∠ABD =AD BD ,∴BD =33x 米. ∵CD -BD =BC ,BC =30米,∴3x -33x =30,解得x =15 3≈25.98(米). 答:无人机飞行的高度AD 约为25.98米.8.解:过点A 作AE ⊥CD 于点E.∵AB =15 m ,∴DE =AB =15 m .∵∠DAE =45°,∴AE =DE =15 m .在Rt △ACE 中,tan ∠CAE =CEAE ,则CE =AE·tan 37°≈15×0.75≈11(m ),∴CD =CE +DE≈11+15=26(m ).答:实验楼的垂直高度即CD 的长约为26 m .9.解:(1)在Rt △ABE 中,BE =AB·tan 31°=31·tan 31°≈18.63(m ),AE =AB cos 31°=31cos 31°≈36.17(m ),则甲楼的高度BE 约为18.63 m ,彩旗的长度AE 约为36.17 m .(2)过点F 作FM ⊥GD ,交GD 于点M.在Rt △GMF 中,GM =FM·tan 19°.在Rt △GDC 中,DG =CD·tan 40°.设甲、乙两楼之间的距离为x m ,则FM =CD =x m ,根据题意,得x tan 40°-x tan 19°≈18.63,解得x≈37.64,则DG≈37.64·tan 40°≈31.58(m ).答:乙楼的高度约为31.58 m ,甲、乙两楼之间的距离约为37.64 m . 10.解:(1)过点M 作MN ⊥AB 交BA 的延长线于点N. ∵OM =1.2米,∠MON =60°, ∴ON =OM·cos 60°=0.6米,∴点M 到地面的距离=ON +OB =0.6+3.3=3.9(米).(2)能.根据题意可得货车的右端应该在图中点E 处,过点E 作EF ⊥BC ,交OM 于点F ,过点O 作OG ⊥EF 于点G.此时BE =3.9-(2.55+0.65)=0.7(米),∴EF =GE +FG =3.3+0.7·tan 30°≈3.704(米),∵3.704>3.5, ∴该货车能安全通过.[素养提升]解:(1)如图①,过点A 作AD ⊥BC ,垂足为D. ∵∠BAC =120°,AB =AC , ∴∠ABC =∠C =30°.令AB =2t cm .在Rt △ABD 中,AD =12AB =t cm ,BD =32AB =3t cm .在Rt △AMD 中,∵∠AMD =∠ABC +∠BAM =45°,∴MD =AD =t cm . ∵BM =BD -MD ,即3t -t =20 3-20,解得t =20,∴AB =2×20=40(cm ). 答:AB 的长为40 cm .(2)如图②,当光线旋转6秒时,设AP 交BC 于点N ,此时∠BAN =15°×6=90°. 在Rt △ABN 中,BN =AB cos 30°=4032=80 33(cm ),∴光线AP 旋转6秒,与BC 的交点N距点B 80 33 cm .如图③,设光线AP 旋转2030秒后光线与BC 的交点为Q.由题意可知,光线从边AB 开始旋转到第一次回到AB 处需120÷15×2=16(秒),而2030=126×16+14,即AP 旋转2030秒与旋转14秒时和BC 边的交点是同一个点Q.旋转14 s 的过程是B→C :8 s ,C→Q :6 s ,∴CQ =BN =80 33 cm .∵AB =AC ,∠BAC =120°,∴BC =2·AB·cos 30°=2×40×32=40 3(cm ),∴BQ =BC -CQ =40 3-80 33=40 33(cm ),∴光线AP 旋转2030秒,与BC 的交点Q 在距点B 40 33cm 处.。