指派问题(含非标准指派问题)
- 格式:doc
- 大小:574.00 KB
- 文档页数:16

指派问题的标准形式是在工作和生活中,我们经常需要指派任务或者解决问题,而指派问题的标准形式对于确保任务顺利完成以及问题得到有效解决起着至关重要的作用。
一个清晰、明确的指派问题标准形式可以帮助我们避免混乱和误解,提高工作效率,达到预期的目标。
首先,指派问题的标准形式应该包括清晰的任务描述。
在指派任务时,必须清楚地描述任务的内容、目标和期限。
这样可以避免任务执行者对任务理解上的偏差,确保任务的准确完成。
同时,任务描述中应该包括所需的资源、工具和支持,以及任务的优先级和重要性,这样可以帮助任务执行者更好地安排工作和资源,提高工作效率。
其次,指派问题的标准形式还应该包括明确的责任人和参与人。
在指派任务时,必须明确指定任务的责任人,以及参与任务的其他相关人员。
责任人需要清楚地知道自己的职责和任务目标,以便能够有效地组织和安排工作。
同时,其他参与人员也需要清楚自己在任务中的角色和责任,以确保任务的协调和合作。
另外,指派问题的标准形式还应包括明确的任务完成标准和验收标准。
任务完成标准是指任务执行者需要达到的具体要求和标准,包括任务的质量、数量、时间等方面的要求。
验收标准是指任务完成后的验收标准,包括验收的程序、标准和方法。
明确的任务完成标准和验收标准可以帮助任务执行者更好地了解任务的要求,确保任务的质量和效果。
最后,指派问题的标准形式还应包括有效的沟通和反馈机制。
在指派任务时,必须建立起有效的沟通和反馈机制,确保任务执行者和相关人员之间的信息畅通和反馈及时。
这样可以帮助任务执行者及时了解任务的进展和问题,及时调整和解决问题,确保任务的顺利完成。
总之,指派问题的标准形式是确保任务顺利完成和问题有效解决的关键。
一个清晰、明确的指派问题标准形式可以帮助我们避免混乱和误解,提高工作效率,达到预期的目标。
因此,在工作和生活中,我们应该重视指派问题的标准形式,做好任务的指派和问题的解决。


指派问题的最优解法指派问题是一个最优化问题,在给定若干个任务和执行者(或机器)的情况下,要求将每个任务指派给一个执行者,并使得总体的执行成本或者效益最优。
指派问题可以用匈牙利算法(Hungarian algorithm)或者KM算法(Kuhn-Munkres algorithm)来求解,这两个算法是目前被广泛采用的指派问题求解方法。
匈牙利算法是一个具有全局优势的贪心算法,它通过不断优化当前的局部选择,最终得到全局最优解。
其基本思想是通过给任务和执行者之间的边标注权重,然后选取最小权重的边进行指派,如果发现某个任务或者执行者已经被指派,就将其它相关的边进行更新,并继续寻找最小权重的边进行指派,直到所有的任务都得到指派。
KM算法是匈牙利算法的一种更加高效的变体。
它首先将指派问题转化为一个最大权匹配问题,然后通过不断调整边的权重,使得每次迭代都可以找到一个指派边的增广路径,并更新相应的匹配结果。
KM算法的核心思想是通过对匹配结果进行调整,减小局部优势并增加全局优势。
无论是匈牙利算法还是KM算法,在最坏情况下的时间复杂度都是O(n^3),其中n表示任务和执行者的数量。
这两个算法的主要区别在于实现的复杂度和算法的效率,KM算法相对于匈牙利算法来说具有更好的性能。
除了匈牙利算法和KM算法之外,还有一些其他的指派问题求解方法,例如启发式搜索、遗传算法等。
这些方法一般适用于指派问题的规模比较大、复杂度比较高的情况下,但是相对于匈牙利算法和KM算法,它们的效率和准确性可能会有所降低。
总之,指派问题的最优解法可以通过匈牙利算法或者KM算法来求解,具体选择哪一种方法可以根据问题的规模和复杂度来决定。

指派问题的四个计算步骤
指派问题是一种优化问题,旨在找到最佳的分配方式。
解决指派问题通常有四个计算步骤:
1. 创建代价矩阵:将问题抽象为一个二维矩阵,其中每个元素表示将某个任务分配给某个工人的成本或者效益。
代价矩阵的大小为n行m列,其中n表示任务的数量,m表示工人的数量。
2. 匹配行和列:通过在代价矩阵中查找每一行和列的最小元素,将其标记为零。
如果需要,通过减去每一行和列的最小元素,可以使矩阵中至少有n个零。
3. 寻找最佳分配方案:通过选择代价矩阵中的一个零,并将其标记为星号,然后将与该零所在行或列相交的所有其他零标记为井号。
如果井号的数量等于n,则找到了一个最佳分配方案。
如果不是,请执行第4步。
4. 修改代价矩阵:通过选择未被标记的最小元素,并从该元素中减去所有未被标记的行和列的最小值,可以修改代价矩阵。
然后,返回第2步继续迭代,直到找到一个最佳分配方案。
这些计算步骤被称为匈牙利算法或者KM算法。
通过依次执
行这些步骤,可以找到指派问题的最优解。

指派问题的求解方法嘿,咱今儿就来聊聊指派问题的求解方法。
你说这指派问题啊,就好像是给一群小伙伴分任务,得让每个人都能分到最合适的事儿,这可不容易嘞!咱先来说说啥是指派问题。
就好比有一堆工作,有几个人可以去做,每个人对不同工作的效率或者效果不一样。
那咱就得想办法,怎么把这些工作分配给这些人,才能让总的效果达到最好呀。
那咋求解呢?有一种方法叫匈牙利算法。
这就好比是一把神奇的钥匙,能打开指派问题的大门。
咱就把那些工作和人当成一个个小格子,通过一些计算和摆弄,找到最合适的搭配。
你想想啊,如果随便分,那可能就浪费了某些人的特长,或者让一些工作没被最合适的人去做,那不就亏大啦?用了这个匈牙利算法,就能一点点地把最合适的工作和人配对起来。
就像你去拼图,得找到每一块的正确位置,才能拼成一幅完整漂亮的图。
这匈牙利算法就是帮咱找到那些正确位置的好帮手呀!它能让那些工作和人都找到自己的“最佳搭档”。
还有啊,咱在生活中也经常会遇到类似的指派问题呢。
比如说,家里要打扫卫生,每个人擅长打扫的地方不一样,那怎么分配任务才能又快又好地打扫完呢?这不就是个小小的指派问题嘛。
或者说在公司里,有几个项目要分给不同的团队,哪个团队最适合哪个项目,这也得好好琢磨琢磨,才能让项目都顺利完成,取得好成果呀。
总之呢,指派问题的求解方法可重要啦,就像我们走路需要一双好鞋一样。
掌握了这些方法,咱就能在面对各种指派问题的时候,不慌不忙,轻松应对,找到那个最优解。
你说是不是很厉害呀?所以啊,可别小瞧了这指派问题的求解方法哦,说不定啥时候就能派上大用场呢!。

非标准指派问题在日常工作中,我们经常会遇到一些非标准指派问题,这些问题可能会给我们的工作带来一些困扰和挑战。
因此,我们需要对这些非标准指派问题进行深入的分析和解决,以便更好地应对各种工作场景。
首先,非标准指派问题可能会出现在项目任务的安排上。
在实际工作中,由于各种原因,我们可能会接到一些非常规的任务指派,这些任务可能与我们的专业领域不太相关,或者超出了我们的工作范围。
面对这种情况,我们需要及时与领导沟通,明确任务的目的和意义,同时也要评估任务的可行性和风险,以便做出正确的决策。
其次,非标准指派问题还可能出现在工作流程的安排上。
在团队协作中,我们可能会遇到一些非常规的工作流程,这些流程可能会影响到我们的工作效率和质量。
为了解决这些问题,我们需要与团队成员进行有效的沟通和协调,找到最适合的工作流程,并在实践中不断进行优化和调整,以确保工作的顺利进行。
此外,非标准指派问题还可能出现在资源分配上。
在工作中,我们可能会面临一些非常规的资源分配问题,例如人力、物力、财力等方面的不足或不合理分配。
为了解决这些问题,我们需要与相关部门或领导进行有效的沟通,协调资源的调配和分配,确保各项工作能够得到充分的支持和保障。
最后,非标准指派问题也可能出现在工作目标的设定上。
在实际工作中,我们可能会接到一些非常规的工作目标,这些目标可能会与我们的实际情况不太符合,或者存在一定的难度和挑战。
为了解决这些问题,我们需要与领导或团队成员进行充分的沟通和协商,明确工作目标的意义和价值,同时也要合理评估目标的可行性和实现路径,以便更好地完成工作任务。
总之,非标准指派问题是我们在工作中经常会遇到的挑战,我们需要以积极的态度和有效的方法来解决这些问题,以便更好地应对各种工作场景,提高工作效率和质量。
希望通过我们的努力,能够更好地应对和解决各种非标准指派问题,为团队的发展和工作的顺利进行贡献力量。

第五章 整数规划§1 整数规划的数学模型及特点要求一部分或全部决策变量必须取整数值得规划问题称为整数规划。
其模型为:Max(或min)z=∑=nj j jx c1s.t ⎪⎪⎩⎪⎪⎨⎧=≥=≥=≤∑=nj nj i ij ij xx x nj x m i b x a ,,,2,10,2,1),(211若要求决策变量只能取值0或1的整数规划称为0-1型整数线性规划。
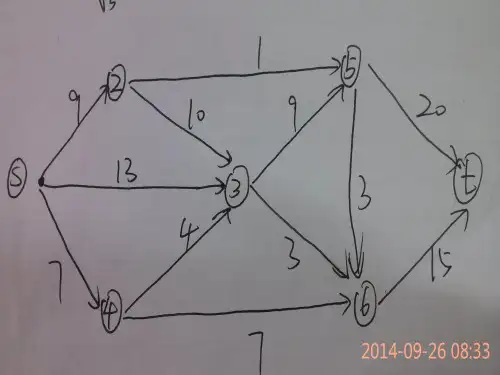
§5 指 派 问 题 一. 指派问题的标准形式及数学模型在现实生活中,有各种性质的指派问题。
例如,有若干项工作需要分配给若干人(或部门)来完成;有若干项合同需要选择若干个投标者来承包;有若干班级需要安排在各教室上课等等。
诸如此类的问题,它们的基本要求是在满足特定的指派要求条件下,使指派方案的总体效果最佳。
由于指派问题的多样性,有必要定义指派问题的标准形式。
指派问题的标准形式(以人和事为例)是:有n 个人和n 件事,已知第i 个人作第j 件事的费用为),2,1,(n j i c ij =,要求确定人和事之间的一一对应的指派方案,是完成这n 件事的总费用最少。
为了建立标准指派问题的数学模型,引入2n 个0-1变量:⎩⎨⎧=10ij x这样,问题的数学模型可写成 ∑∑===ni nj ij ijx cz 11min (5.1)s.t ⎪⎪⎪⎩⎪⎪⎪⎨⎧======∑∑==n j i x n i x n j x ij n j ij n i ij ,2,1,1,0,2,11,2,1111 (5.3)其中,(5.1)表示每件事必优且只有一个人去做,(5.2)表示每个人必做且只做一件事。
注:○1 指派问题是产量(i a )、销量(j b )相等,且i a =j b =1,i ,j=1,2,…n 的运输中部分或全部取整数 若指派第i 人作第j 件事若不指派第i 人作第j 事i ,j=1,2,…n(5.2) (5.4)问题。
○2 有时也称ijc 为第i 个人完成第j 件工作所需的资源数,称之为效率系数(或价值系数)。

第一章绪论1、指派问题的背景及意义指派问题又称分配问题,其用途非常广泛,比如某公司指派n个人去做n 件事,各人做不同的一件事,如何安排人员使得总费用最少?若考虑每个职工对工作的效率(如熟练程度等),怎样安排会使总效率达到最大?这些都是一个企业经营管理者必须考虑的问题,所以该问题有重要的应用价值.虽然指派问题可以用0-1规划问题来解,设X(I,J)是0-1变量, 用X(I,J)=1表示第I个人做第J件事, X(I,J)=0表示第I个人不做第J件事. 设非负矩阵C(I,J)表示第I个人做第J件事的费用,则问题可以写成LINGO程序SETS:PERSON/1..N/;WORK/1..N/;WEIGHT(PERSON, WORK): C, X ;ENDSETSDATA:W=…ENDDATAMIN=@ SUM(WEIGHT: C*X);@FOR(PERSON(I): @SUM(WORK(J):X(I,J))=1);@FOR(WORK(J): @SUM(PERSONM(I):X(I,J))=1);@FOR(WEIGHT: @BIN(X));其中2*N个约束条件是线性相关的, 可以去掉任意一个而得到线性无关条件.但是由于有N^2个0-1变量, 当N很大时,用完全枚举法解题几乎是不可能的. 而已有的0-1规划都是用隐枚举法做的,计算量较大. 对于指派问题这种特殊的0-1规划,有一个有效的方法——匈牙利算法,是1955年W. W. Kuhn利用匈牙利数学家D.König的二部图G的最大匹配的大小等于G的最小顶点覆盖的大小的定理提出的一种算法,这种算法是多项式算法,计算量为O(N3).匈牙利算法的基本原理是基于以下两个定理.定理1设C=(C ij)n×n是指派问题的效益矩阵,若将C中的任一行(或任一列)减去该行(或该列)中的最小元素,得到新的效率矩阵C’,则C’对应的新的指派问题与原指派问题有相同的最优解.证明:设X’是最优解, 即@SUM(WEIGHT: C*X’)<= @SUM(WEIGHT: C*X), 则当C中任一行或任一列减去该行或该列的最小数m时,得到的阵C’还是非负矩阵, 且@SUM(WEIGHT: C’*X’)<=@SUM(WEIGHT: C*X)-m=@SUM(WEIGHT: C’*X)定理2效率矩阵C中独立的0元素的最多个数等于覆盖所有0元素的最少直线数. 当独立零元素的个数等于矩阵的阶数时就得到最优解.3、理论基础定义:图G的一个匹配M是图G中不相交的边的集合. 属于匹配M中的边的所有端点称为被该匹配M饱和, 其他的顶点称为M-未饱和的. 如果一个匹配M 饱和了图G的所有顶点,则称该匹配M是一个完全匹配. 可见顶点数是奇数的图没有完全匹配. 一个匹配M称为是极大匹配, 如果它不能再扩张成更大的一个匹配. 一个匹配称为是最大匹配, 如果不存在比它更大的匹配.定义:对于一个匹配M, 图G的一个M-交替路是图G中的边交替地在M中及不在M中的边组成. 从M-未饱和点出发到M-为饱和点结束的M-交替路称为一条M-增广路. 把M-增广路中不是M中的边改成新的匹配M’中的边, 把M-增广路中M中的边不作为M’中的边, 在M-增广路以外的M中的边仍作为M’中的边, 则M’的大小比M大1. 故名M-增广路. 因此最大匹配M不存在M-增广路.定义:若图G和图H有相同的顶点集V, 我们称G和H的对称差,记为G∆H,是一个以V为顶点集的图, 但其边集是G和H的边集的对称差: E(G∆H)=E(G) ∆E(H)=E(G)⋂E(H)-(E(G)⋃E(H))=(E(G)-E(H)) ⋂ (E(H)-E(G))定理: (Berge, 1957) 图G的一个匹配M是最大匹配,当且仅当G中没有M-增广路.证明: 我们只要证明, G中没有M-增广路时, M是最大匹配. 用反证法, 若有一个比M大的匹配M’. 令G的一个子图F, E(F)=M∆M’, 因M和M’都是匹配, F的顶点的最大度数至多是2, 从而F由不相交的路和环组成, 它们的边交替地来自M和M’, 于是F中的环的长度是偶数. 由于M’比M大, F中存在一个连通分支,其中M’中的边数大于M中的边数. 这个分支只能是起始和终止的边都在M’中. 而这就是一条G中的M-增广路. 与假设矛盾. 证毕.定理(Hall, 1935)设G是一个二部图, X和Y是其二分集, 则存在匹配M 饱和X当且仅当对于X中的任意子集S, Y 中与S中的点相邻的点组成的集合N(S)中元素的个数大于等于集合S中元素的个数.证明:必要性是显然的. 对于充分性, 假设 |N(S)|≥|S|, ∀S⊂X, 考虑G的一个最大匹配M, 我们用反证法,若M没有饱和X, 我们来找一个集合S不满足假设即可. 设u∈X是一个M-未饱和顶点, 令S⊂X和T⊂Y分别是从u出发的M-交替路上相应的点.我们来证明M中的一些边是T到S-u上的一个匹配. 因为不存在M-增广路,T中的每个点是M-饱和的. 这意味着T中的点通过M中的边到达S中的一个顶点. 另外, S-u中的每个顶点是从T中的一个顶点通过M中的一条边到达的. 因此M 中的这些边建立了T与S-u的一个双射, 即|T|=|S-u|. 这就证明了M中的这些边是T到S-u上的一个匹配,从而意味着T⊂N(S), 实际上, 我们可证明T=N(S). 这是因为连接S和Y-T中的点y的边是不属于M的, 因为不然的话, 就有一条到达y的M-增广路, 与y∉T矛盾. 故|N(S)|=|T|=|S-u|=|S|-1<|S|, 与假设矛盾.当X与Y的集合的大小相同时的Hall定理称为婚姻问题,是由Frobenius(1917)证明的.推论: k-正则的二部图(X的每一点和Y的每一点相关联的二部图)(k>0)存在完全匹配.证明: 设二分集是X,Y. 分别计算端点在X和端点在Y的边的个数, 得k|X|=k|Y|, 即|X|=|Y|.因此只要证明Hall的条件成立即可. 使X饱和的匹配就是完全匹配. 考虑∀S⊂X, 设连接S与N(S)有m条边, 由G的正则性, m=k|S|. 因这m条边是与N(S)相关联的, m≤k|N(S)|, 即k|S|≤ k|N(S)|, 即|N(S)|≥|S|. 这就是Hall的条件.用求M-增广路的方法来得到最大匹配是很费时的. 我们来给出一个对偶最优化问题.定义:图G的一个顶点覆盖是集合S⊂V(G), 使得G的每条边至少有一个端点在S中. 我们称S中的一个顶点覆盖一些边, 若这个顶点是这些边的公共端点.因为匹配的任意两条边不能被同一个顶点覆盖, 所以顶点覆盖的大小不小于匹配的大小: |S|≥|M|. 所以当|S|=|M| 时就同时得到了最大的匹配和最小的顶点覆盖.定理(König [1931],Egerváry[1931])二部图G的最大匹配的大小等于G的最小顶点覆盖的大小.证明: 设M是G的任一个匹配, 对应的二分集是X,Y. 设U是一个最小的顶点覆盖, 则|U|≥|M|, 我们只要由顶点覆盖U来构造一个大小等于|U|的匹配即完成证明. 令R=U⋃X, T=U⋃Y, 令H, H’分别是由顶点集R⋂(Y-T)及T⋂(X-R)诱导的G的子图. 我们应用Hall的定理来证明H有一个R到Y-T中的完全匹配,H’有一个从T到X-R中的完全匹配. 再因这两个子图是不相交的, 这两个匹配合起来就是G中的一个大小为|U|的匹配.因为R⋂T是G的一个覆盖, Y-T与X-R之间没有边相联接. 假设S⊂R, 考虑在H中S的邻接顶点集N(S), N(S) ⊂Y-T. 如果|N(S)|<|S|, 因为N(S)覆盖了不被T覆盖的与S相关联所有边, 我们可以把N(S) 代替S作为U中的顶点覆盖而得到一个更小的顶点覆盖. U的最小性意味着H中Hall条件成立. 对H'作类似的讨论得到余下的匹配. 证毕.最大匹配的增广路算法输入: 一个二分集为X,Y的二部图G,一个G中的匹配M, X中的M-未饱和顶点的集合U.思路: 从U出发探求M-交替路,令S⊂X,T⊂Y为这些路到达过的顶点集. 标记S中不能再扩张的顶点. 对于每个x∈(S⋂T)-U, 记录在M-增广路上位于x前的点.初始化: S=U,T=∅.叠代: 若S中没有未标记过的顶点, 结束并报告T⋂(X-S)是最小顶点覆盖而M是最大匹配.不然, 选取S中未标记的点x, 考虑每个y∈N(x)且xy∉M, 若y是M-未饱和的, 则得到一个更大的匹配,它是把xy加入原来的匹配M得到的,将x从S中去除. 不然, y是由M中的一条边wy相连接的, w∈X, 把y加入T(也有可能y本来就在T中), 把w加入S. w未标记, 记录w前的点是y. 对所有关联到x的边进行这样的探索后, 标记x. 再次叠代.定理: 增广路算法可以得到一个相同大小的匹配和顶点覆盖.证明: 考虑这个算法终止的情况, 即标记了S中所有的点. 我们要证明R=T⋂(X-S)是大小为|M|的一个顶点覆盖.从U出发的M-交替路只能通过M中的边进入X中的顶点, 所以S-U中的每个顶点通过M与T中的顶点匹配, 并且没有M中的边连接S和Y-T. 一旦一条M-交替路到达x∈S, 可以继续沿着任何未饱和的边进入T, 由于算法是对于x的所有邻域顶点进行探索才终止的,所以从S 到Y-T 没有未饱和边. 从而S 到Y-T 没有边, 证明了R 是一个顶点覆盖.因为算法是找不到M-增广路时终止, T 的每一个顶点是饱和的. 这意味着每个顶点y ∈T 是通过M 匹配与S 中的一个顶点. 由于U ⊂S, X-S 的每个顶点是饱和的, 故M 中与X-S 相关联的边不和T 中的点相连接. 即它们与是饱和T 的边不同的, 这样我们可见M 至少有|T|+|X-S|条边. 因不存在一个比顶点覆盖更大的匹配, 所以有|M|=|T|+|X-S|=|R|.设二部图G 的二分集X 和Y 都是n 个元素的点集, 在其边j i y x 上带有非负的权ij w , 对于G 的一个匹配M, M 上各边的权和记作w(M).定义: 一个n ×n 矩阵A 的一个横截(transversal)是A 中的n 个位置, 使得在每行每列中有且只有一个位置(有的文献中把横截化为独立零元素的位置来表示).定义: 指派问题就是给定一个图G=n n K ,(完全二部图, 即每个X 中的顶点和Y 中的每个顶点有边相连接的二部图)的边的权矩阵A, 求A 的一个横截, 使得这个横截上位置的权和最大. 这是最大带权匹配问题的矩阵形式.定义: 对于图G=n n K ,,设其二分集是X ,Y ,给定G 的边j i y x 的n ×n 权矩阵W={ij w }.考虑G 的子图v u G ,, 设其二分集是U ⊂X ,V ⊂Y, 边集是E(v u G ,), 对于子图v u G ,的带权覆盖u,v 是一组非负实数{i u },{j v },使得ij j i w v u ≥+,)(,v u j i G E y x ∈∀, v u G ,的带权覆盖的费用是∑∑+j i v u 记为C(u,v), 最小带权覆盖问题就是求一个具有最小费用C(u,v)的带权覆盖u,v.引理: 若M ⊂E(v u G ,)是一个带权二部子图v u G ,的最大匹配, 且u, v 是v u G ,的带权覆盖, 则C(u,v)≥w(M). 而且, C(u,v)=w(M)当且仅当ij j i w v u =+,M y x j i ∈∀. 这时M 是v u G ,最大带权匹配, u,v 是v u G ,的最小带权覆盖, 定义这时的v u G ,为G 的相等子图(equality subgraph ).证明: 因为匹配M 中的边是不相交的, 由带权覆盖的定义就得C(u,v)≥w(M). 而且C(u,v)=w(M)当且仅当ij j i w v u =+,M y x j i ∈∀成立. 因一般地有C(u,v)≥w(M).所以当C(u,v)=w(M)时. 意味着没有一个匹配的权比C(u,v)大, 也没有一个覆盖的费用比w(M)小.Kuhn 得到一个指派问题的算法,命名为匈牙利算法, 为的是将荣耀归于匈牙利数学家König 和Egerv áry.指派问题的匈牙利算法(Kuhn[1955], Munkres[1957]):输入G=n n K ,的边的权矩阵A, 及G 的二分集X,Y.初始化: 任取一个可行的带权覆盖,例如)(max ij ji w u =,0=j v ,建立G 的相等子图v u G ,, 其二分集是X, Y ’⊂Y, 求v u G ,的一个最大匹配M. 这个匹配的权和w(M)=C(u,v), M 的带权覆盖是具有最小费用的.叠代: 如M 是G 的一个完全匹配, 停止叠代, 输出最大带权匹配M. 不然, 令U 是X 中的M-未饱和顶点. 令S ⊂X, T ⊂Y 是从U 中顶点出发的M-交替路到达的顶点的集合.令},:min{T Y y S x w v u j i ij j i -∈∈-+=ε.对于所有的S x i ∈, 将i u 减少ε, 对于所有的T y j ∈,将j v 增加ε,形成新的带权覆盖u ’,v ’及对应的新的相等子图v u G '',.如果这个新的相等子图含有M-增广路, 求它的最大匹配M ’, 不然不改变M 再进行叠代.定理: 匈牙利算法能找到一个最大权匹配和一个最小费用覆盖.证明: 算法由一个覆盖开始,算法的每个叠代产生一个覆盖,仅在相等子图有一个完全的匹配为止。
《第五章 整数规划§1 整数规划的数学模型及特点要求一部分或全部决策变量必须取整数值得规划问题称为整数规划。
其模型为:Max(或min)z=∑=nj j jx c1⎪⎪⎩⎪⎪⎨⎧=≥=≥=≤∑=nj nj i ij ij xx x nj x m i b x a ,,,2,10,2,1),(211~若要求决策变量只能取值0或1的整数规划称为0-1型整数线性规划。
§5 指 派 问 题 一. 指派问题的标准形式及数学模型在现实生活中,有各种性质的指派问题。
例如,有若干项工作需要分配给若干人(或部门)来完成;有若干项合同需要选择若干个投标者来承包;有若干班级需要安排在各教室上课等等。
诸如此类的问题,它们的基本要求是在满足特定的指派要求条件下,使指派方案的总体效果最佳。
由于指派问题的多样性,有必要定义指派问题的标准形式。
指派问题的标准形式(以人和事为例)是:有n 个人和n 件事,已知第i 个人作第j 件事的费用为),2,1,(n j i c ij =,要求确定人和事之间的一一对应的指派方案,是完成这n 件事的总费用最少。
为了建立标准指派问题的数学模型,引入2n 个0-1变量:⎩⎨⎧=10ij x这样,问题的数学模型可写成 ∑∑===ni nj ij ijx cz 11min ()⎪⎪⎪⎩⎪⎪⎪⎨⎧======∑∑==n j i x n i x n j x ij n j ij n i ij ,2,1,1,0,2,11,2,1111 ()"中部分或全部取整数\若不指派第i 人作第j 事i ,j=1,2,…n() ()其中,()表示每件事必优且只有一个人去做,()表示每个人必做且只做一件事。
注:○ 指派问题是产量(i a )、销量(j b )相等,且i a =j b =1,i ,j=1,2,…n 的运输问题。
○ 有时也称ij c 为第i 个人完成第j 件工作所需的资源数,称之为效率系数(或价值系数)。
并称矩阵C= n n ij c ⨯)(=⎪⎪⎪⎪⎪⎭⎫⎝⎛nn n n n n c c c c c cc c c 212222111211() 为效率矩阵(或价值系数矩阵)。
并称决策变量ij x 排成的n ×n 矩阵X=n n ij x ⨯)(= ⎪⎪⎪⎪⎪⎭⎫⎝⎛nn n n n n x x x x x xx x x 212222111211 ()为决策变量矩阵。
…的特征是它有n 个1,其它都是0。
这n 个1位于不同行、不同列。
每一种情况为指派问题的一个可行解。
共n!个解。
其总的费用 z =C ⊙X这里的⊙表示两矩阵对应元素的积,然后相加。
问题是:把这n 个1放到X 的2n 个位置的什么地方可使耗费的总资源最少(解最优) 例1 已知效率矩阵C= ⎪⎪⎪⎪⎪⎭⎫⎝⎛0084765000320205则X (1)= ⎪⎪⎪⎪⎪⎭⎫⎝⎛010*********0010, X (2)= ⎪⎪⎪⎪⎪⎭⎫⎝⎛1000000101000010^都是指派问题的最优解例12/P-149:某商业公司计划开办五家新商店。
为了尽早建成营业,商业公司决定由5家建筑公司分别承建。
已知建筑公司A i (i=1,2,…5)对新商店B j (1,2,…5)的建造费用的报价(万元)为ij c (i ,j=1,2,…5),见表5-9。
商业公司应当对5家建筑公司怎样分派建筑任务,才能使总的建筑费用最少表5-9解:这是一标准的指派问题。
若设0-1变量 ;ij x =⎩⎨⎧01则问题的数学模型为Min z=411x +812x +…+1054x +655x⎪⎪⎪⎩⎪⎪⎪⎨⎧======∑∑==5,2,1,1,05,2,115,2,115151 j i x i x j x ij j ij i ij;若看成运输问题,且ij x 如上所述,则表5-9为当A i 承建B j 时 当A i 不承建B j 时i,j=1,2,当然,第一行的1应放在(1,1)位置,此位置同时是第一列的费用最小。
但一般情况下没有这么好。
需找一适合一般的方法。
二. 匈牙利解法原理:虽然指派问题是一类特殊的整数规划问题,又是特殊的0-1规划问题和特殊的运输问题,因此,它可以用多种相应的解法来求解。
但是,这些解法都没有充分利用指派问题的特殊性质,有效地减少计算量。
1955年,库恩()提出了匈牙利法。
—定理1:设指派问题的效率矩阵为C= n n ij c ⨯)(,若将该矩阵的某一行(或某一列)的各个元素都减去统一常数t (t 可正可负),得到新的效率矩阵n n ijc C ⨯'=')(,则以C '为效率矩阵的新的指派问题与原指派问题的最优解相同。
但其最优解比原最优解之减少t.证明:设式()~()为原指派问题。
现在C 矩阵的第k 行个元素东减去同一常数t,记新的指派问题的目标函数为Z '.则有Z '=∑=ni 1∑='n j ijijx c 1=∑≠=n k i i 1∑='n j ij ij x c 1+∑='n j ij ij x c 1=∑≠=n k i i 1∑=nj ij ijx c1+∑=-nj kj kj x t c 1)(=∑≠=n ki i 1∑=nj ij ijx c1+∑=nj kj kj x c 1-t ∑=n j kj x 1=∑=ni 1∑=nj ij ijx c1-t ·1=Z-t因此有Min Z '=min(Z-t)=minZ-t而新问题的约束方程同原指派问题。
因此其最优解比相同,而最优解差一个常数。
推论:若将指派问题的效率矩阵每一行即每一列分别减去各行及各列的最小元素,则得到新指派问题与原指派问题有相同的最优解。
!证明:结论是显然的。
只要反复运用定理1便可得证。
当将效率矩阵的每一行都减去各行的最小元素,将所得的矩阵的每一列在减去当前列中最小元素,则最后得到新效率矩阵C '中必然出现一些零元素。
设ijc '=0,从第i 行来看,它表示第i 个人去干第j 项工作效率(相对)最好。
而从第j 列来看,这个0表示第j 项工作以第i 人来干效率(相对)最高。
定义:在效率矩阵C 中,有一组在不同行不同列的零元素,称为独立零元素组,此时每个元素称为独立零元素。
例2: 已知C= ⎪⎪⎪⎪⎪⎭⎫⎝⎛0084765000320205则{12c =0,24c =0,31c =0,43c =0}是一个独立零元素组,12c =0,24c =0,31c =0,43c =0分别称为独立零元素。
{12c =0,23c =0,31c =0,44c =0}也是一个独立零元素组,而{14c =0,23c =0,31c =0,44c =0}就不是一个独立零元素组,因为14c =0与44c =0这两个零元素位于同一列中。
根据以上对效率矩阵中零元素的分析,对效率矩阵C 中出现的的独立零元素组中零元素所处的位置,在决策变量矩阵中令相应的ij x =1,其余的ij x =0。
就可找到指派问题的一个最优解。
就上例中 $X (1)= ⎪⎪⎪⎪⎪⎭⎫⎝⎛010*********0010, 就是一个最优解。
同理X (2)= ⎪⎪⎪⎪⎪⎭⎫⎝⎛1000000101000010 也是一个最优解。
但是在有的问题中发现效率矩阵C 中独立零元素的个数不够n 个,这样就无法求出最优指派方案,需作进一步的分析。
首先给出下述定理。
定理2 效率矩阵C 中独立零元素的最多个数等于能覆盖所有零元素的最少直线数。
我们不证它,说一下意思: 例3:已知矩阵 @C 1= ⎪⎪⎪⎪⎪⎭⎫⎝⎛0084765000320205,C 2= ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛5636040084275500003220205,C 3= ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛341404008653300003420207分别用最少直线去覆盖各自矩阵中的零元素:C 1= ⎪⎪⎪⎪⎪⎭⎫⎝⎛0084765000320205, C 2= ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛5636040084275500003220205, C 3= ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛341404008653300003420207可见,C 1最少需要4条线,C 2最少需要4条线,C 3最少需要5条线,方能划掉矩阵中所有的零。
即它们独立零元素组中零元素最多分别为4,4,5。
三. 匈牙利法求解步骤:我们以例题来说明指派问题如何求解: 例4 给定效率矩阵 ·C= ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛9118713161491514410413152求解该指派问题。
解:ⅰ)变换效率矩阵,将各行各列都减去当前各行、各列中最小元素。
C= ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛9118713161491514410413152 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛24104750111006211130 ⎪⎪⎪⎪⎪⎭⎫⎝⎛00102350960607130= C '这样得到的新矩阵C '中,每行每列都必然出现零元素。
)ⅱ)用圈0法求出新矩阵C '中独立零元素。
(1)进行行检验对C '进行逐行检验,对每行只有一个未标记的零元素时,用○记号将该零元素圈起。
然后将被圈起的零元素所在的列的其它未标记的零元素用记号×划去。
如C '中第2行、第3行都只有一个未标记的零元素,用○分别将它们圈起。
然后用×划去第1列其它未被标记行变换 2 4 9 % min列变换 Min 0 0 4 2的零元素(第2列没有),见C ''C ' ⎪⎪⎪⎪⎪⎭⎫⎝⎛00102350960607130=C ''在第i 行只有一个零元素ij c =0时,表示第i 人干第j 件工作效率最好。
因此优先指派第i 人干第j 项工作,而划去第j 列其它未标记的零元素,表示第j 项工作不再指派其它人去干(即使其它人干该项工作也相对有最好的效率)。
重复行检验,直到每一行都没有未被标记的零元素或至少有两个未被标记的零元素时为止。
本题C ''中第1行此时也只有1个未被标记的零元素。
因此圈起C ''中第1行第4列的零元素14c ,然后用×划去第4列中未被标记的零元素。
这是第4行也只有一个未被标记的零元素43c ,再用○圈起,见C '''C '' ⎪⎪⎪⎪⎪⎭⎫⎝⎛00102350960607130=C ''' ?(2)进行列检验与进行行检验相似,对进行了行检验的矩阵逐列进行检验,对每列只有一个未被标记的零元素,用记号○将该元素圈起,然后技改元素所在行的其他未被标记的零元素打×。