如何在SAS中实现R×C列联表的两两比较

多个样本及其两两比较的秩和检验SAS程序多个样本及其两两比较的秩和检验SAS程序广东医学院预防医学教研室(524023)丁元林孔丹莉秩和检验是医学实践中较为常用的一大类非参数统计方法,目前国内几本较具权威性SAS专著11,22,均介绍了秩和检验的一些SAS程序,宇氏132也作了进一步的探讨和总结,但对于不同资料类型和特征的多个样本比较的秩和检验SAS程序阐述得不够全面,而且几乎未涉及到两两比较的SAS程序,但实际工作者往往对两两比较的结果更为感兴趣。

为此,本文结合实例,根据常见类型资料的特点,给出了多个样本及其两两比较的秩和检验SAS程序。

11成组设计的原始数据多个样本及其两两比较这种类型资料一般为成组设计的定量资料,但各个样本的总体呈偏态分布或方差不齐,且未整理成其他形式(如频数表),检验其总体分布是否相同的常用秩和检验方法是Kruska-l Wallis法,在SAS软件中实现的过程步有以下三种:NPAR1WAY过程、FREQ 过程以及RANK和ANOVA两过程的结合。

各个样本两两比较一般可通过RANK和ANOVA两过程的结合,采用M EANS语句来实现。

对文献142第139页表1中的数据进行Kruska-l Wallis检验及两两比较的SAS程序如下: /*以下为建立数据库*/data dy1;do group=1to3;input x@@;output;end;cards;918016014101211211910162102121310 214215141031121814184113111516510 3171516519319211671441624101316710;/*以下为调用F REQ过程*/proc fr eq;t ables group*x/scores=rank cmh2noprint;/*以下为调用N PAR1WAY过程*/proc npar1way w ilcoxon;class group;v ar x;/*以下为调用RA NK过程*/proc rank data=dy1out=a;v ar x;ranks r;/*以下为调用A NOV A过程*/proc anova;class group;model r=group;means group/lsd;r un;以上程序中调用FREQ过程产生的第二个CMH 统计量、NPAR1WAY过程产生的卡方统计量以及ANOVA过程产生的R2与T 总之积,即为为Kruska-l Wallis检验结果。

【宝典】R×C列联表（分类数据）的统计分析方法选择与SPSS实现分类资料在医学统计中很常见，有些统计学书上称为计数资料，比如（有效、无效），（发病、不发病），（男、女），血型（A、B、O、AB）等等。

分类资料一般根据频数整理成列联表的形式，一般的列联表多是二维的（也称行列表，或R×C列联表，高维列联表下次讨论），列联表根据变量是否有序可以分为双向无序、单项有序、双向有序列联表，统计方法是不同的，分析如下：一、双向无序列联表（一）成组四格表是指行、列变量均为无序的列联表，例如要研究吸烟和肺癌之间的关系，行变量为是否吸烟：吸烟、不吸烟，列变量为肺癌发病：发病，不发病，如下表：发生肺癌未发生肺癌吸烟a b不吸烟 c d对于这种数据，我们的统计目的是分析行列变量的独立性，即：肺癌发病是否与吸烟有关，可选用的方法有以下两种：1、Pearson卡方检验：基于卡方分布，H0为行、列变量相互独立，SPSS中“分析->描述性统计->交叉表”可实现。

四格表使用条件：专用公式①样本总数大于40；②各个单元格理论值均大于5。

校正公式：①样本总数大于40；②理论值1<T<5;Fisher确切概率法：①样本总数小于40，或T<1，无需选择，软件自动计算成组四格表Fisher。

2、Fisher精确概率：基于超几何分布，当数据不满足Pearson卡方检验时使用。

SPSS 中“分析->描述性统计->交叉表”可实现。

注意SPSS仅提供了2×2表的精确概率，需要计算R×C列联表的精确概率，可以选择精确按钮中的蒙特卡罗近似法实现。

（一）成组R×C表(双向无序)A型B型O型AB型A地区 a b c dB地区 e f j hC地区i j k l1.Pearson卡方检验条件：不能有任何一个格子的理论频数T<1,同时1<T<5的格子数不能超过总格子数的1/5.如若不符合：可以增加研究样本量（通常少用）；对理论频数较小的行或者列进行合并或者删除；采用R×C表的Fisher确切概率法（通常采用蒙特卡洛近似法）2.R×C表Fisher确切概率法操作：分析—描述—交叉表—设置好行列变量—点击精确—选择蒙特卡洛。

在R语言中，有多种方法可以进行三组间的两两比较。

以下是一些常见的方法：1. t检验（pairwise.t.test）：当数据满足正态性和方差齐性假设时，可以使用t检验来进行两两比较。

该函数会对每对组进行t检验，计算出每对之间的差异显著性水平和置信区间。

```Rpairwise.t.test(data$group, data$value, p.adjust.method = "bonferroni")```2. 方差分析（ANOVA）：如果数据不满足t检验的假设条件，可以使用方差分析来进行两两比较。

可以使用ANOVA函数进行方差分析，然后使用posthoc函数进行多重比较。

```Rmodel <- aov(value ~ group, data = data)posthoc <- TukeyHSD(model)```3. 非参数检验（Kruskal-Wallis检验）：当数据不满足正态性和方差齐性假设时，可以使用非参数方法进行两两比较，如Kruskal-Wallis检验。

可以使用kruskal.test函数进行Kruskal-Wallis检验，然后使用pairwise.wilcox.test函数进行多重比较。

```Rkruskal.test(value ~ group, data = data)pairwise.wilcox.test(data$value, data$group, p.adjust.method = "bonferroni")```这些方法都可以用于进行三组间的两两比较，具体应该根据数据的性质和实验设计来选择合适的方法。

在进行多重比较时，通常需要考虑到多重比较校正以控制错误率。

常见的多重比较校正方法包括Bonferroni校正、Holm校正等。

A14-如何在SAS中实现R×C列联表的两两比较内容来自网络，侵删在分析R×C列联表时，在卡方检验有统计意义的情况下常常需要做进一步的多重比较。

可以采用的方法为1）卡方分割（具体见本人另外一篇文章《R×C行列表卡方值分割的概念及运用》）将原表卡方值分割成独立的子卡方值，分割后的子卡方值和对应的自由度相加会和原表的卡方值和自由度相等。

2）或者采用彼此之间非独立的两两比较。

但是两两比较的卡方值和对应的自由度相加不会等于原表卡方值和自由度，所以此类比较不能称为卡方分割法。

尽管后者更为灵活但需要调整多重比较的次数以避免增加第一类错误。

本文将具体讲解如何在SAS中实现R×C列联表的两两比较。

1．研究数据-血型和疾病类型假定某医学课题想研究血型(O,A,B)和疾病类型(Peptic Ulcer, Gastric Cancer,Control)是否相互关联, 具体临床数据见表1。

表1：血型和疾病类型行列表Disease TypeBloodType Peptic Ulcer(I)-1 Gastric Cancer(II)-2 Control(III)-3 Total O-1983(14.024)383(4.9139)2892(1.4159)4258A-2679(9.0743)416(4.5484)2625(0.679)3720B-3134(4.6663)84(0.2695)570(0.9519)788Totals17968836087N=87662．初步分析我们先用SAS/PROC FREQ 和PROC CORRESP 先对数据做初步的分析，来判断行列变量之间的关系。

CELLCHI2 选项是计算按公式2-1计算每个单元格在总体值的组成。

2χij ijijji E OE C 2,)(-=（2-1）proc freq data=paper14;weight count;table r*c/chisq cellchi2nopercent;run;proc corresp data=paper14;weight count;les r, c;tabrun;表2 – 卡方检验结果Table of r by cr cFrequencyCell Chi-SquareRow PctCol Pct 123Total198314.02423.0954.733834.91398.9943.3728921.415967.9247.51425826799.074318.2537.814164.548411.1847.1126250.67970.5643.12372031344.666317.017.46840.269510.669.515700.951972.349.36788Total 179688360878766 Statistics for Table of r by cStatistic DF Value Prob ------------------------------------------------------ Chi-Square 4 40.5434 <.0001 Likelihood Ratio Chi-Square 4 40.6401 <.0001 Mantel-Haenszel Chi-Square 1 21.0035 <.0001 Sample Size = 8766从表２中可以看出第１行（血型Ｏ）的卡方检验分值在所有行中所占比重最高（(14.024+4.9139+1.4159)/40.5434≈50％）;第１列（Peptic Ulcer(I)）的卡方检验分值在所有列中所占比重最高（(14.024+9.0743+4.6663)/40.5434≈68.5%）。

如何用SAS软件正确分析生物医学科研资料XX. R × C列联表资料的统计分析与SAS软件实现(三)王琪;胡良平;柳伟伟【摘要】生物统计学是生物学领域科学研究和实际工作中必不可少的工具，在分子生物学迅速发展的今天，生物统计学更显示出了它的重要性。

实验设计与数据统计分析是现代生物学的基石，是生物学研究者检验假说、寻找模式、建立生物学理论的有利工具，也是生物学研究者探索微观和宏观生物世界的必备基础知识。

对于每天甚至是每时每刻涌现的大量的、以天文数字计量的分子遗传数据，必须借助统计学知识加以分析处理，才能从中获得有意义的信息。

“生物多样性数据分析”是开展生物多样性研究的一个重要方面，数据分析能力的高低极大地影响着我们对各种生态学现象认识的深度和广度。

现在，电子计算机的普及使得生物统计分析过程大大简化，生物统计分析软件包的普及将生物统计学从统计学家的书本里解放了出来，简化了生物统计分析过程，使之成为生物学研究者的常用工具。

本刊特邀军事医学科学院生物医学统计学咨询中心主任胡良平教授，以“如何用 SAS 软件正确分析生物医学科研资料”为题，撰写系列统计学讲座，希望该系列讲座能对生物医学科研工作者有所帮助。

【期刊名称】《中国医药生物技术》【年(卷),期】2012(000)006【总页数】3页(P469-471)【作者】王琪;胡良平;柳伟伟【作者单位】100850 北京,军事医学科学院生物医学统计学咨询中心;100850 北京,军事医学科学院生物医学统计学咨询中心;100850 北京,军事医学科学院生物医学统计学咨询中心【正文语种】中文XX. R × C列联表资料的统计分析与SAS软件实现（三）编者按生物统计学是生物学领域科学研究和实际工作中必不可少的工具，在分子生物学迅速发展的今天，生物统计学更显示出了它的重要性。

实验设计与数据统计分析是现代生物学的基石，是生物学研究者检验假说、寻找模式、建立生物学理论的有利工具，也是生物学研究者探索微观和宏观生物世界的必备基础知识。

SPSS超详细操作：卡⽅检验（R×C列联表）医咖会之前推送过⼀些卡⽅检验相关的⽂章，包括：卡⽅检验(2x2)、卡⽅检验(2xC)、配对卡⽅检验、分层卡⽅检验等。

今天我们再和⼤家分享⼀下，如何⽤SPSS来做RxC列联表的卡⽅检验。

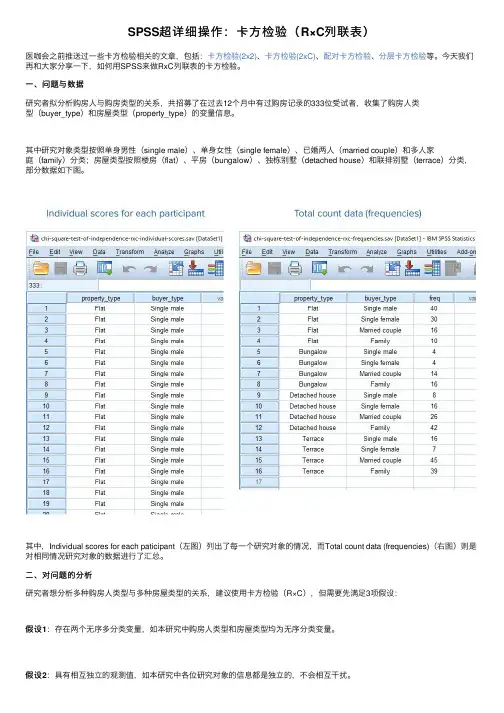
⼀、问题与数据研究者拟分析购房⼈与购房类型的关系，共招募了在过去12个⽉中有过购房记录的333位受试者，收集了购房⼈类型（buyer_type）和房屋类型（property_type）的变量信息。

其中研究对象类型按照单⾝男性（single male）、单⾝⼥性（single female）、已婚两⼈（married couple）和多⼈家庭（family）分类；房屋类型按照楼房（flat）、平房（bungalow）、独栋别墅（detached house）和联排别墅（terrace）分类，部分数据如下图。

其中，Individual scores for each paticipant（左图）列出了每⼀个研究对象的情况，⽽Total count data (frequencies)（右图）则是对相同情况研究对象的数据进⾏了汇总。

⼆、对问题的分析研究者想分析多种购房⼈类型与多种房屋类型的关系，建议使⽤卡⽅检验（R×C），但需要先满⾜3项假设：假设1：存在两个⽆序多分类变量，如本研究中购房⼈类型和房屋类型均为⽆序分类变量。

假设2：具有相互独⽴的观测值，如本研究中各位研究对象的信息都是独⽴的，不会相互⼲扰。

假设3：样本量⾜够⼤，最⼩的样本量要求为分析中的任⼀期望频数⼤于5。

本研究数据符合假设1和假设2，那么应该如何检验假设3，并进⾏卡⽅检验（R×C）呢？三、SPSS操作1. 数据加权如果数据是汇总格式（如上图中的Total count data），则在进⾏卡⽅检验之前，需要先对数据加权。

如果数据是个案格式（如上图中的Individual scores for each paticipant），则可以跳过“数据加权”步骤，直接进⾏卡⽅检验的SPSS操作。

A14-如何在SAS中实现R×C列联表的两两比较内容来自网络，侵删在分析R×C列联表时，在卡方检验有统计意义的情况下常常需要做进一步的多重比较。

可以采用的方法为1）卡方分割（具体见本人另外一篇文章《R×C行列表卡方值分割的概念及运用》）将原表卡方值分割成独立的子卡方值，分割后的子卡方值和对应的自由度相加会和原表的卡方值和自由度相等。

2）或者采用彼此之间非独立的两两比较。

但是两两比较的卡方值和对应的自由度相加不会等于原表卡方值和自由度，所以此类比较不能称为卡方分割法。

尽管后者更为灵活但需要调整多重比较的次数以避免增加第一类错误。

本文将具体讲解如何在SAS中实现R×C列联表的两两比较。

1．研究数据-血型和疾病类型假定某医学课题想研究血型(O,A,B)和疾病类型(Peptic Ulcer, Gastric Cancer,Control)是否相互关联, 具体临床数据见表1。

表1：血型和疾病类型行列表Disease TypeBloodType Peptic Ulcer(I)-1 Gastric Cancer(II)-2 Control(III)-3 Total O-1983(14.024)383(4.9139)2892(1.4159)4258A-2679(9.0743)416(4.5484)2625(0.679)3720B-3134(4.6663)84(0.2695)570(0.9519)788Totals17968836087N=87662．初步分析我们先用SAS/PROC FREQ 和PROC CORRESP 先对数据做初步的分析，来判断行列变量之间的关系。

CELLCHI2 选项是计算按公式2-1计算每个单元格在总体值的组成。

2χij ijijji E OE C 2,)(-=（2-1）proc freq data=paper14;weight count;table r*c/chisq cellchi2nopercent;run;proc corresp data=paper14;weight count;les r, c;tabrun;表2 – 卡方检验结果Table of r by cr cFrequencyCell Chi-SquareRow PctCol Pct 123Total198314.02423.0954.733834.91398.9943.3728921.415967.9247.51425826799.074318.2537.814164.548411.1847.1126250.67970.5643.12372031344.666317.017.46840.269510.669.515700.951972.349.36788Total 179688360878766 Statistics for Table of r by cStatistic DF Value Prob ------------------------------------------------------ Chi-Square 4 40.5434 <.0001 Likelihood Ratio Chi-Square 4 40.6401 <.0001 Mantel-Haenszel Chi-Square 1 21.0035 <.0001 Sample Size = 8766从表２中可以看出第１行（血型Ｏ）的卡方检验分值在所有行中所占比重最高（(14.024+4.9139+1.4159)/40.5434≈50％）;第１列（Peptic Ulcer(I)）的卡方检验分值在所有列中所占比重最高（(14.024+9.0743+4.6663)/40.5434≈68.5%）。

多组等级资料比较的秩和检验及组间两两比较的SAS实现郭志武【摘要】目的探讨多组等级资料的秩和检验及组间两两比较的SAS实现.方法结合实例介绍多组等级资料Kruskal-Wallis H检验和两两比较Nemenyi检验的计算方法和步骤,通过编制SAS程序一次性完成Kruskal-Wallis H检验和Nemenyi 检验.结果运行SAS程序得到可靠结果.结论编制SAS程序可以有效实现多组等级资料的秩和检验及组间两两比较.【期刊名称】《中国医院统计》【年(卷),期】2018(025)003【总页数】2页(P233-234)【关键词】等级资料;秩和检验;两两比较;SAS【作者】郭志武【作者单位】518033 深圳市中医院【正文语种】中文多组独立样本等级资料是临床常见的资料类型。

针对多组独立样本等级资料比较的假设检验通常采用Kruskal-Wallis H检验，若检验结果具有统计学意义，则可以进一步采用Nemenyi检验进行组间两两比较[1]。

Kruskal-Wallis H检验利用通用的统计软件可以完成，但Nemenyi检验却不能直接从统计软件包的集成功能或模块中完成，需要另外编写自定义程序。

刘伟等采用SPSS菜单操作结合编程实现了Nemenyi检验[2]，本文通过编制SAS程序一次性完成Kruskal-Wallis H检验和Nemenyi检验。

1 方法与步骤参考文献[1]已详细介绍了Kruskal-Wallis H检验和Nemenyi检验的原理、方法和步骤。

本文只针对多组独立样本的等级资料结合实例介绍计算方法和步骤。

文献[1]第131页实例如下：4种疾病患者痰液内嗜酸性粒细胞的检查结果见表1。

问4种疾病患者痰液内嗜酸性粒细胞有无差别？表1 4种疾病患者痰液内嗜酸性粒细胞比较嗜酸性粒细胞(1)支气管扩张(2)肺水肿(3)肺癌(4)病毒性呼吸道感染(5)合计(6)秩范围(7)平均秩(8)-0353111～116+25751912～3021 ++95332031～5040.5+++62201051～6055.5Ri739.5 436.5 409.5 244.5 ni17 15 17 11 60Ri 43.5029.1024.0922.23(1)首先进行Kruskal-Wallis H检验检验统计量H按以下公式计算：(1)式中,ni为各样本例数，N为样本总例数(N=∑ni)，Ri为各样本秩和。

R×C表资料的R×CR×C表⼜称为⾏×列表, 其检验⽤于多个样本率的⽐较、两个或多个构成⽐的⽐较、以及双向⽆序分类资料的关联性检验。

基本数据有三种情况：①多个样本率⽐较时，有R⾏2列，称为R×2表；②两个样本的构成⽐⽐较时，有2⾏R列，称2×R表；③多个样本的构成⽐⽐较，以及双向⽆序分类资料关联性检验时，有R⾏C列，称为R×C表。

2、⾏×列表资料的卡⽅检验⾏×列表资料的卡⽅检验⽤于多个率或多个构成⽐的⽐较。

1）专⽤公式：r⾏c列表资料卡⽅检验的卡⽅值=2)应⽤条件：要求每个格⼦中的理论频数T均⼤于5或1但在使⽤时须注意，简化计算公式只有在所有Tij均⼤于5的情况下使⽤。

若出现⼀个理论数⼩于1的格⼦，或1处理的⽅法继续观察，适当扩⼤样本量。

②将邻近有意义的(或性质相同)分类进⾏合并，以适当增加频数，满⾜计算公式的应R×C 表的分类及其检验⽅法的选择R×C表可分为双向⽆序、单向有序、双向有序属性相同和双向有序属性不同4类。

1．双向⽆序R×C表R×C表中两个分类变量皆为⽆序分类变量。

对于该类资料：①若研究⽬的为多个样本率（或构成⽐）⽐较，可⽤⾏×列表资料的检验；②若研究⽬的为分析两个分类变量之间有⽆关联性以及关系的密切程度时，可⽤⾏×列表资料的检验以及Pearson列联系数进⾏分析。

2．单向有序R×C表①R×C表分组变量（如年龄）是有序的，⽽指标变量（如传染病的类型）是⽆序的；研究⽬的通常是多个构成⽐的⽐较，如分析不同年龄组传染病的构成情况；此时可⽤⾏×列表资料的检验分析。

3．双向有序属性相同的R×C表R×C表中的两分类变量皆为有序且属性相同。

实际上是2×2配对设计的扩展，即⽔平数≥3的诊断试验配伍设计，如⽤两种检测⽅法对同⼀批样品的测定结果。

一元析因设计分析两两比较的sas程序设计
SAS程序设计步骤：
1. 导入数据：使用SAS的数据提取功能，从关系数据库或文本文件中提取数据，并将其导入到SAS的数据集中。

2. 数据清理：使用SAS的数据清理功能，清理数据，确保数据的准确性和可用性。

3. 建立变量：使用SAS的变量建立功能，建立用于分析的变量，以便进行两两比较。

4. 运行分析：使用SAS的分析功能，运行两两比较分析，以获得有关变量之间的比较结果。

5. 结果报告：使用SAS的报告功能，创建有关两两比较分析结果的报告，以供查看和分析。

231行×列表分析 第 13 章同R ×C 表资料。

对于双向有序属性不同R ×C 表资料，有3种分析目的，所以也就有3种相应的统计分析方法。

其一，只关心试验分组变量取不同水平时，有序的结果变量之间的差别是否有显著性意义，采用单向有序列联表的分析方法。

其二，希望研究两个有序变量之间是否有相关关系，就需要运用定性资料的相关分析方法，包括Spearman 秩相关分析和典型相关分析。

其三，如果两个有序变量之间有相关关系，需要迚一步研究两个变量之间是否呈直线变化关系，这就需要迚行线性趋势检验。

对于和双向有序属性相同R ×C 表资料，研究的目的通常是分析两种检测方法的一致性，此时宜用一致性检验（或称Kappa 检验），也可以用特殊模型分析方法（可用SAS 软件）。

一致性检验见四栺表的一致性检验。

与处理配对设计2×2表资料的思路一样，除了对方表资料作一致性检验外，还可以对两种检测方法的检测结果不一致部分作比较，此时称为“对称性检验”（在分析配对设计2×2表资料时，叫做McNemar's Test ）。

13.4.1 行列均为顺序变量的相关检验介绍变量虽然是有序的，但毕竟还不是定量的，需要给有序变量的各等级赋值，方可迚行相关分析。

最简单的赋值法是按顺序赋给秩次（即得分），即给行变量的等级赋值1，2，…，R 和给列变量的等级赋值1，2，…，C 。

这样(X,Y)的不同取值就有R×C 对，表中的R×C 个频数就是这R×C 对取值所对应的频数，然后计算Spearman 秩相关系数，幵作显著性检验，这是比较粗糙的分析方法。

Spearman 秩相关分析比较粗糙，这是因为它给有序变量的等级赋值过于简单，不能最大限度地获得有序变量之间的相关信息。

而典型相关分析是在使有序变量的相关达到极大的前提下给有序变量的各等级赋值，就是对于表的边缘（指“行合计”与“列合计”）设法产生一双变量正态，从而迚行相关分析。