当前位置：文档之家 › 剪切扭转的内力与强度计算 习题

剪切扭转的内力与强度计算 习题

  • 格式：doc
  • 大小：80.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

材料力学扭转练习题

材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴，主动轮A的输入功率为PA =0 kW，从动轮B，C，D，E的输出功率分别为PB =0 kW，PC = kW，PD = 10 kW，PE = 1kW。

则轴上最大扭矩T。

A．BA段 B．AC段 C．CD段 D．DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。

题2图3. 上题图示单元体的应力状态中属正确的是。

4. 下列关于剪应力互等定理的论述中正确的是。

A．剪应力互等定理是由平衡B．剪应力互等定理仅适用于纯剪切的情况C．剪应力互等定理适用于各种受力杆件D．剪应力互等定理仅适用于弹性范围E．剪应力互等定理与材料的性能无关5. 图示受扭圆轴，其横截面上的剪应力分布图正确的是。

-12-题5图6. 实心圆轴，两端受扭转外力偶作用。

直径为D时，设轴内的最大剪应力为?，若轴的直径改为D2，其它条件不变，则轴内的最大剪应力变为。

A．8? B．?C．16? D．?7. 受扭空心圆轴，在横截面积相等的条件下，下列承载能力最大的轴是。

A．??0 B．??0.5C．??0. D．??0.88. 扭转应力公式T?的适用范围是。

IpA．各种等截面直杆 B．实心或空心圆截面直杆C．矩形截面直杆 D．弹性变形 E．弹性非弹性范围 9. 直径为D的实心圆轴，最大的容许扭矩为T，若将轴的横截面积增加一倍，则其最大容许扭矩为。

A．2TB．2T C．22TD．4T10. 材料相同的两根圆轴，一根为实心，直径为D1；另一根为空心，内径为d2，外径为D2d2D??。

若两轴横截面上的扭矩T，和最大剪应力?max均相同，则两轴外径之比1 D2D2为。

A．1??B．1?? C．343D．411. 阶梯圆轴及其受力如图所示，其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。

A．?max1??max2B．?max1?313?max2C．?max1??max2D．?ma x1??max248-13-题12图题13图12. 在图示的圆轴中，AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。

扭转强度计算

扭转强度计算

工程背景
工程背景
工程背景
6.3 扭转强度计算 ——思路
6.3 扭转强度计算 ——内容
建立圆轴扭转时横截面上的应力公式 理解公式，分析应力分布规律 建立强度条件（类比轴向拉压变形） 应用解决强度计算问题
建立圆轴扭转时 横截面上的应力公式
两个假设 平面假设 横截面间距不变假设 三种关系 变形几何关系 物理关系 静力学关系
MD0.96kNm，已知材料的许用切应力 80MPa
试校核该轴的强度。
解：用截面法求得BA、AC、CD段的扭矩，并
绘出扭矩图如图所示。
因为传动轴为等截面，所以最大切应力发生在 AC段内各截面周边上各点。
m axT W m a p x 1 .7 6 ( 0 1 .0 0 5 3N m ) 3 m 7 1 .7 1 0 6P a7 1 .7 M P a
横截面上任一点切应力的计算公式
τρ
Tρ Ip
T（或Mn）——横截面上的扭矩
ρ——待求点到圆心的距离
Ip——截面对其形心的极惯性矩
IP 2dA A
分析应力分布规律
横截面上任一点切应力大小同ρ呈正比
m ax
Tr Ip
Wp
Ip r
——抗扭截面系数
max
T
Wp
思考及练习
思考： 实心圆轴纯扭转时，如何破坏？ 从外向内，逐层破坏
练习： 例题6-2
建立强度条件
横截面最大切应力不超过材料的许用切应力
τmax τ
τ max
Tmax Wp
塑性材料： 0 .5 0 .6
脆性材料： 0 .8 1 .0
强度计算理论
强度校核 截面设计 许用荷载计算
max

剪切实用计算例题

剪切实用计算例题
2F n 3.98 d 2 [ j ]
（2）铆钉的挤压计算
jy
Fb F /n [ jy ] A jy t1d
F n 3.72 t1d [ jy ]
材料力学
剪切实用计算
因此取 n=4. I F/n F/n
（3）主板拉断的校核。 危险截面为I-I截面。 F 主板的强度条件为（忽略
x l时，FN ,max Al
（2）应力
m
x
m
x

o
FN ( x) ( x) A
FN ( x) FN max FN
x
max xl l
由强度条件：
max [ ]
l
[ ]

拉伸与压缩/轴向拉（压）时的变形
FN ( x) dFN
dx m x dx
拉应力:
P [ ] 2 d 4 材料力学
(1) 得： (2) (1) d [ ] 4 2.4 h [ ] (2) 挤压应力: P bs 2 (D d 2 ) 4
P
剪切实用计算
例题3-4 两矩形截面木杆，用两块钢板连接如图示。已知拉杆的 截面宽度 b=25cm，沿顺纹方向承受拉力F=50kN，木材的顺纹许 用切应力为 [ j ] 1MPa , 顺纹许用挤压应力为 [ jy ] 10 MPa 。试求 接头处所需的尺寸L和 。
别为 [ j ] 100MPa， [ jy ] 280MPa 。若F=250kN，试求 （1）每边所需的铆钉个数n；
（2）若铆钉按图(b)排列，所需板宽b为多少？
F F
材料力学
剪切实用计算
F
F
图(a) F
F
图(b)

扭转典型习题解析

扭转典型习题解析

扭转典型习题解析1 一内径d =100mm 的空心圆轴如图示，已知圆轴受扭矩m kN 5⋅=T ，许用切应力][τ=80MPa ，试确定空心圆轴的壁厚。

解题分析：因为不知道壁厚,所以不能确定是不是薄壁圆管。

分别按薄壁圆管和空心圆轴设计。

解： 1、按薄壁圆管设计薄壁圆管扭转时，假设切应力沿壁厚均匀分布，设壁厚为δ，平均半径为2/0）（δ+=d R ，则扭转切应力为 δτ20π2R T=强度条件为][ττ≤，于是得][π22τδδTd =+）（ ][π22223τδδδTd d =++ ()Pa1080πm N 1052m 10100m 1010026323233××⋅××=×+××+−−δδδ解得 mm 70.3m 1070.33=×=−δ 2、按空心圆轴设计强度条件为 ][pmax ττ≤=W T将δ216π44p +=−=d D d D DW ）；（代入得][π16][π][π164444=−−≤−τττd TD D d D DT，）（0Pa)108(m 1.0πm N 10516Pa 1080π64346=××−×⋅××−×××）（D D解得mm 107.7m 10107.73=×=−Dmm 85.32mm100mm 7.1072=−=−=d D δ 比较可知，两种设计的结果非常接近。

讨论: 当10/0R ≤δ时，即认为是薄壁圆管，可以直接使用薄壁管扭转公式。

2 图示受扭圆杆，沿平面ABCD 截取下半部分为研究对象，如图b 所示。

试问截面ABCD 上的切向内力所形成的力偶矩将由哪个力偶矩来平衡？解题分析：由切应力互等定理可知截面ABCD 上的切向内力分布及其大小。

该截面上切向内力形成一个垂直向上的力偶矩。

在图b 中，左右两个横截面上的水平切向内力分量形成垂直于截面ABCD 的竖直向下的力偶矩，正好与截面ABCD 上切向内力的合力偶矩平衡。

材料力学扭转练习题

材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴，主动轮A的输入功率为PA =0 kW，从动轮B，C，D，E的输出功率分别为PB =0 kW，PC = kW，PD = 10 kW，PE = 1kW。

则轴上最大扭矩T。

A．BA段 B．AC段 C．CD段 D．DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。

题2图3. 上题图示单元体的应力状态中属正确的是。

4. 下列关于剪应力互等定理的论述中正确的是。

A．剪应力互等定理是由平衡B．剪应力互等定理仅适用于纯剪切的情况C．剪应力互等定理适用于各种受力杆件D．剪应力互等定理仅适用于弹性范围E．剪应力互等定理与材料的性能无关5. 图示受扭圆轴，其横截面上的剪应力分布图正确的是。

-12-题5图6. 实心圆轴，两端受扭转外力偶作用。

直径为D时，设轴内的最大剪应力为?，若轴的直径改为D2，其它条件不变，则轴内的最大剪应力变为。

A．8? B．?C．16? D．?7. 受扭空心圆轴，在横截面积相等的条件下，下列承载能力最大的轴是。

A．??0 B．??0.5C．??0. D．??0.88. 扭转应力公式T?的适用范围是。

IpA．各种等截面直杆 B．实心或空心圆截面直杆C．矩形截面直杆 D．弹性变形 E．弹性非弹性范围 9. 直径为D的实心圆轴，最大的容许扭矩为T，若将轴的横截面积增加一倍，则其最大容许扭矩为。

A．2TB．2T C．22TD．4T10. 材料相同的两根圆轴，一根为实心，直径为D1；另一根为空心，内径为d2，外径为D2d2D??。

若两轴横截面上的扭矩T，和最大剪应力?max均相同，则两轴外径之比1 D2D2为。

A．1??B．1?? C．343D．411. 阶梯圆轴及其受力如图所示，其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。

A．?max1??max2B．?max1?313?max2C．?max1??max2D．?ma x1??max248-13-题12图题13图12. 在图示的圆轴中，AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。

理论力学扭转例题

理论力学扭转例题

,
题解：
由于B端固定，φB¹ 则有: =0
B
T1 a GI P T2 (a b) GI P TB (a b c) GI P
2
0
T1 2
式中设TB与T1同向，代入 T 其中： a c 得 T 5T1 B
8
4
b
2
（与假设方向相反）
画出图如图所示。
12tl
2
题13：图示一实心钢轴插入一铜管中，设彼此之间无摩 擦力，A端用一销钉连接，此时B端轴与管的销钉相差φ 角，施加外力偶使轴与管相对转动，插入另一销钉，已 知：轴长为l，实心钢轴的抗扭刚度为GIp，铜管的抗扭刚 度为轴的2倍，求移去外力偶后轴与管的内力。
题解：
设轴和管的扭矩分别为T1 和T2
39、题解:
M x 0
有
T 0
Dt
D 2

2T
D t
2
'
由剪应力互等定律，纵截面上的 纵向截面上的总剪力

'
，
Q l t l t
n Q A 2T
由铆钉的剪切强度条件，有
D A
2
一、剪应力流的方向与扭矩的方向一致。
x
4
1 32T l 1 1 d d d d 3 d 3 0 GI x 3G b p a a b Tdx
题7：若圆截面轴AB，其左端固定，承受 均布力矩 t 作用，试导出该轴B端的扭转 角。 题解：
二、开口薄壁截面杆在自由扭转时的剪应力分布如图（a），厚 度中点处，应力为零。
当h/b>10时，截面为狭长矩形： =1/3

(仅供参考)第十九章-扭转的强度与刚度计算

(仅供参考)第十九章-扭转的强度与刚度计算

一、外力偶矩的计算
前面已经指出 ，使轴产生扭转变形的是外力偶矩。但是作用于轴上的外力偶矩往
往不是直接给出的，而是给定轴所传递的功率和轴的转速。以图 19-3 所示的传动轴为例，
由电动机的转速和功率可以求出传动轴 AB 的转速及通过皮带轮输入的功率。功率由皮
带轮传到轴 AB 上，再经右端的齿轮输出。设通过皮带轮给 AB 轴输入的功率为 N（kW），
因为 1kW=1000N·m/s 因此每秒钟输入功应为 ： W = N ×1000(N ⋅ m)
（a）
电动机是通过皮带轮以力偶矩 Me 作用于 AB 轴上的，若 AB 轴的转速为每分钟 n 转，
则力偶矩 Me 在每秒内完成的功应为 ：
W = 2π × n × Me(N ⋅ m)
(b)
60
因为 Me 所完成的功也就是皮带轮给 AB 轴输入的功，故（a）、（b）两式应相等，这
据微元的平衡要求，不仅左右一对面上有大小相等，方向相反的剪应力 τ ，在上下一对
面也必须有剪应力τ ′ ，而且由力矩平衡条件 ∑ mz = 0 有：
(τtdy)dx = (τ ′tdx)dy
由此得到：
τ =τ′
（19-2）
这表明，在相互垂直的两个微面上，剪应力总是成对出现的，它们数值相等，而方
向均垂直于两微面的交线，或指向或背离这一交线。这就是剪应力互等定理。
利用第三节中的（b）式和（c）式，上式可以写成：
φ
φ
图 19-9
u = 1 τγ 2
再由剪切胡克定律（式 19-3）得：
u = 1 τγ = τ 2 2 2G
46
第四节 圆轴扭转时的应力与变形
一、横截面上剪应力计算公式
圆轴扭转时，在已知横截面上的扭矩后，还应进一步研究横截面上的应力分布规律，

材料力学复习例题

材料力学复习例题
1 P 2 3 P
t
P
d
t
P/4
1
2
3
工程力学教程电子教案
20
1
2
3 P
3板(杆)拉伸强度计算 板 杆 拉伸强度计算
σ max =
FN P = (b 2 d )t Amin
3
1 110 × 10 = = 200 MPa ≥ [σ ] 4 (8 . 5 1 .6 × 2 ) × 1 × 10
P/4
一拉伸压缩 1,轴力图 2,强度条件应用:校核,设计,计算 3,低碳钢拉伸实验,应力-应变曲线 4,连接件强度:剪切,挤压实用计算
例题
30 kN A B 3 30 kN A 2
3
B 2
作轴力图. 要作ABCD杆的 作轴力图. 解:要作 杆的 20 kN 20 kN 轴力图, 轴力图,则需分别将 C D AB,BC,CD杆的轴 杆的轴 20 kN 1 20kN 力求出来.分别作截 力求出来. x 1 面1-1,2-2,3-3,如 , , , D C 20kN 左图所示. 左图所示. F
Me B
(a)
(b)
图示为一受集中荷载F作用的简支 图示为一受集中荷载 作用的简支 试作其剪力图和弯矩图. 梁.试作其剪力图和弯矩图. a F b 根据整体平衡, 解:根据整体平衡,求 A B 得支座约束力 C FA FB x FA=Fb/l, FB=Fa/l
例
梁上的集中荷载将 梁分为AC和 两段 两段, 梁分为 和CB两段, 根据每段内任意横截面 左侧分离体的受力图容 易看出, 易看出,两段的内力方 程不会相同. 程不会相同.
σ x1 σ x2
σ x3
FNx1 400 × 10 3 = = 160 × 10 6 Pa = 160MPa = 6 A1 2500 × 10 FNx 2 -100 × 10 3 = = -40 × 10 6 Pa = -40MPa = A2 2500 × 10 6

最新弯曲的内力与强度计算习题

最新弯曲的内力与强度计算习题

弯曲的内力与强度计算一、判断题1.如图1示截面上，弯矩M和剪力Q的符号是：M为正，Q为负。

（）图12.取不同的坐标系时，弯曲内力的符号情况是M不同，Q相同。

（）3、在集中力作用的截面处，Q图有突变，M连续但不光滑。

（）4、梁在集中力偶作用截面处，M图有突变，Q图无变化。

（）5.梁在某截面处，若剪力Q=0，则该截面的M值一定为零值。

（）6.在梁的某一段上，若无荷载作用，则该梁段上的剪力为常数。

（）7.梁的内力图通常与横截面面积有关。

（）8.应用理论力学中的外力定理，将梁的横向集中力左右平移时，梁的Q 图，M图都不变。

（）9.将梁上集中力偶左右平移时，梁的Q图不变，M图变化。

（）10.图2所示简支梁跨中截面上的内力为M≠0，Q=0。

（）图 2 图 311.梁的剪力图如图3所示，则梁的BC段有均布荷载，AB段没有。

（）12.上题中，作用于B处的集中力大小为6KN，方向向上。

（）13.右端固定的悬臂梁，长为4m，M图如图示，则在x=2m处，既有集中力又有集中力偶。

（）图 4 图 514.上题中，作用在x=2m处的集中力偶大小为6KN·m，转向为顺时针。

（）15.图5所示梁中，AB跨间剪力为零。

（）16.中性轴是中性层与横截面的交线。

（）17.梁任意截面上的剪力，在数值上等于截面一侧所有外力的代数和。

（）18.弯矩图表示梁的各横截面上弯矩沿轴线变化的情况，是分析梁的危险截面的依据之一。

（）19.梁上某段无荷载作用，即q=0，此段剪力图为平行x的直线；弯矩图也为平行x轴的直线。

（）20.梁上某段有均布荷载作用，即q=常数，故剪力图为斜直线；弯矩图为二次抛物线。

（）21.极值弯矩一定是梁上最大的弯矩。

（）22.最大弯矩Mmax只可能发生在集中力F作用处，因此只需校核此截面强度是否满足梁的强度条件。

（）23.截面积相等，抗弯截面模量必相等，截面积不等，抗弯截面模量必不相等。

（）24.大多数梁都只进行弯曲正应力强度核算，而不作弯曲剪应力核算，这是因为它们横截面上只有正应力存在。

第三节圆轴剪切与扭转变形_化工设备机械类

第三节圆轴剪切与扭转变形_化工设备机械类

12
挤压面积的计算
d
挤压力
t Fbs
Abs=td
bs
Fbs Abs
计算挤压面
①挤压面为平面，计算挤压面就是该面
②挤压面为弧面，取受力面对半径的投 影面
13
§3-1 剪切与挤压
§3.1.3 剪切与挤压强度计算
剪应力强度条件： FS
A
挤压强度条件：
bs
Fbs Abs
bs
塑性材料： 0.6 0.8 bs 1.7 2
脆性材料： 0.8 1.0 bs 0.9 1.5
14
§3-1 剪切与挤压
§3.1.3 剪切与挤压强度计算
A
A向
B向
B
注意：实际挤压面 是半圆柱
剪力FS
挤压力Fbs 剪力作用 面积
挤压力计算 面 积 Abs
剪应力 — 1、计算面积是剪力的真实作用区
2、名义剪应力是真实的平均剪应力
挤压应力 — 1、计算面积不一定是挤压力真实作用区 2、名义挤压应力不一定是平均挤压应力
m1
m4
n
A
B
C
D
T
– –
4.78
6.37
x
9.56
38
§3.2.3 扭转时内力的计算
39
§3-3 圆轴扭转时的应力
•分析圆轴扭转时的应力需要考虑三方面的关系：一是 变形几何关系；二是应力应变关系；三是静力学关系。 一、利用几何关系求剪应变分布规律
1、实验观察和假设推论
40
41
实验现象：
（1）各圆周线的形状、大小以及两圆周线间的距离均无 变化，只是绕轴线转了不同的角度； （2）所有纵向线仍近似地为一条直线，只是都倾斜了同 一个角度，使原来的矩形变成平行四边形。

材料力学剪切习题

材料力学剪切习题
6
14 . 8 MPa [ ] 90 MPa
（2） 校核 挤压强度 挤压面上的挤压力为
P 188 KN
挤压面的计算面积为
Abs 1 d 11 9 99 10
4
m
2
所以工作挤压应力为
bs
P Abs 188 1000 99 10
4
19 10 Pa
11 . 76 10
m
所以，平键的工作剪应力为

Q A 12100 11 . 76 10
4
10 . 3 10 Pa 10 . 3 MP a [ ] 87 MPa
6
满足剪切强度条件。
（2） 校核 挤压强度
与轴和键比较，通常轮毂抵抗挤压的能力较弱。轮毂挤压面上的 挤压力为
P=12100N 挤压面的面积与键的挤 压面相同，设 键与轮毂的接触高度为 h/2，则挤压面面积（图 2-10f）为
Abs h 2 lp
4
1 .6 2 m
2
( 7 .0 2 1 .4 )
3 . 36 10
Abs
h 2
lp
4
1 .6 2 m
2
( 7 . 0 2 1 . 4 ) 3 . 36 cm
2
3 . 36 10
故轮毂的工作挤压应力为
bs
P Abs 12100 3 . 36 10
4
36 10 Pa
6
36 MPa [ j ] 100 MPa
也满足挤压强度条件。 所以，这一键连接的剪切强度和挤压强度都是足够的。
高炉热风围管套环和吊杆通过销轴连接，每个吊杆上 承重P=188kN,销轴直径d=90mm,吊杆端部厚1=110mm,套 环厚2=75mm,材料皆为A3钢， []=90MPa， [bs]=200MPa，试校核销轴连接强度。

材料力学第三章剪切和扭转

材料力学第三章剪切和扭转

T
Ⅰ
T
d1
(a)
l
T (b)
D2
Ⅱ
T
l
36
3.3 等直圆杆扭转时的应力
解：
Wp1

πd13 16
Wp2
πD23 14
16
1,maxW Mpt11
T Wp1
16T πd13
2,ma xW M pt2 2W Tp2πD 2 311T 6 4
D 2 31 4 d 1 3
螺栓连接[图(a）]中，螺栓主要受剪切及挤压（局部压
缩）。
F
3
3.1 剪切
键连接[图(b）]中，键主要受剪切及挤压。
4
3.1 剪切
剪切变形的受力和变形特点： 作用在构件两侧面上的外力的合力大小相等、方向相 反，作用线相隔很近，并使各自推动的部分沿着与合 力作用线平行的受剪面发生错动。
受剪面上的内力称为剪力； 受剪面上的应力称为切应力；
3.3 等直圆杆扭转时的应力
传动轴的外力偶矩：
已知：
T2
T1
从动轮
n 主动轮
T3 从动轮
传动轴的转速 n ；某一轮上 所传递的功率
NK (kW)
作用在该轮上的外力偶矩T 。
一分钟内该轮所传递的功率等于其上外力偶矩所 作的功：
NK60 13 0(J)T2πn(Nm)
33
3.3 等直圆杆扭转时的应力
26
3.3 等直圆杆扭转时的应力
dj M t
d x GI pBiblioteka G djdx
GGMItp

Mt
Ip
等直圆杆扭转时横截面上切应力计算公式
Mt

O

工程力学习题册第五章 - 答案

工程力学习题册第五章 - 答案

第五章拉伸和压缩一、填空题1.轴向拉伸或压缩的受力特点是作用于杆件两端的外力__大小相等___和__方向相反___，作用线与__杆件轴线重合_。

其变形特点是杆件沿_轴线方向伸长或缩短__。

其构件特点是_等截面直杆_。

2.图5-1所示各杆件中受拉伸的杆件有_AB、BC、AD、DC_，受压缩的杆件有_BE、BD__。

图5-13.内力是外力作用引起的，不同的__外力__引起不同的内力，轴向拉、压变形时的内力称为_轴力__。

剪切变形时的内力称为__剪力__，扭转变形时的内力称为__扭矩__，弯曲变形时的内力称为__剪力与弯矩__。

4.构件在外力作用下，_单位面积上_的内力称为应力。

轴向拉、压时，由于应力与横截面__垂直_，故称为__正应力__；计算公式σ＝F N/A_；单位是__N/㎡__或___Pa__。

1MPa＝__106_N/m2＝_1__N/mm2。

5.杆件受拉、压时的应力，在截面上是__均匀__分布的。

6.正应力的正负号规定与__轴力__相同，__拉伸_时的应力为__拉应力__，符号为正。

__压缩_时的应力为__压应力_，符号位负。

7.为了消除杆件长度的影响，通常以_绝对变形_除以原长得到单位长度上的变形量，称为__相对变形_，又称为线应变，用符号ε表示，其表达式是ε＝ΔL/L。

8.实验证明：在杆件轴力不超过某一限度时，杆的绝对变形与_轴力__和__杆长__成正比，而与__横截面面积__成反比。

9.胡克定律的两种数学表达式为σ＝Eε和ΔL＝F N Lo/EA。

E称为材料的_弹性模量__。

它是衡量材料抵抗_弹性变形_能力的一个指标。

10.实验时通常用__低碳钢__代表塑性材料，用__灰铸铁__代表脆性材料。

11.应力变化不大，应变显著增大，从而产生明显的___塑性变形___的现象，称为__屈服___。

12.衡量材料强度的两个重要指标是__屈服极限___和__抗拉强度__。

13.采用___退火___的热处理方法可以消除冷作硬化现象。

工程力学下题库

工程力学下题库

工程力学题库一、填空题（每空1分，共57分）（难度A）第八章轴向拉伸和压缩1. "强度"是构件在外力作用下____________ 的能力。

2. 通常，各种工程材料的许用切应力[T不大于其____________ 切应力。

3. 在材料力学中，对可变形固体的性质所作的基本假设是假设、___________________ 设和 ______________ 假设。

4. 衡量材料强度的两个重要指标是_______________ 和_____________________ 。

5. 由于铸铁等脆性材料的很低，因此，不宜作为承拉零件的材料。

6. 在圆轴的台肩或切槽等部位，常增设_____________________ 结构，以减小应力集中。

7. 消除或改善是提高构件疲劳强度的主要措施。

第九章剪切与扭转1. 应用扭转强度条件，可以解决_______________________ 、 _____________________ 和_____________ _____ —等三类强度计算问题。

2. 在计算梁的内力时，当梁的长度大于横截面尺寸____________ 倍以上时，可将剪力略去不计。

3. 若两构件在弹性范围内切应变相同，则切变模量G值较大者的切应力较______________ 。

4. 衡量梁弯曲变形的基本参数是___________________ 和________________________ 。

5. 圆轴扭转变形时的大小是___________________________________ 用来度量的。

6. 受剪切构件的剪切面总是___________ 于外力作用线。

7. 提高圆轴扭转强度的主要措施：______________________ 和__________________ 。

8. 如图所示拉杆头为正方形，杆体是直径为d圆柱形。

1. 作用在梁上的载荷通常可以简化为以下三种类型：___________ 、2. 按照支座对梁的约束情况，通常将支座简化为三种形式：______3. 根据梁的支承情况，一般可把梁简化为以下三种基本形式：____4. ___________________________ 对梁的变形有两种假设：、______________________________________ 。

剪切和扭转的强度计算

剪切和扭转的强度计算

解： AC段：
A C 1 3kN.m 2 B 2kN.m T2 扭矩图 3kN.m ⊕ 2kN.m
○ -
m 0 m 0
T1 3 0; T1 3kN.m
BC段：
Hale Waihona Puke T1T2 2 0; T2 2kN.m
7
二、圆截面杆扭转时的应力
Mn Ip
实心圆截面的极惯性距： IP
学习情境五 剪切和扭转杆的强度计算
甘肃省有色冶金职业技术 学 院
子情境一 剪切强度计算
一、剪切的概念
2
二、剪切强度的实用计算
剪切面上的内力可用截面法求的。假想将铆钉沿剪切面截开 分为上下两部分，任取其中一部分为研究对象，由平衡条件知， 剪切面上的内力必然与外力方向相反，大小由平衡方程得V=F
这种平行于截面的内力V称为剪力。
5
2、圆截面杆扭转时横截面上的内力—扭矩
一、扭矩
圆杆扭转横截面的内力合成 结果为一合力偶，合力偶的力偶
Ⅰ
矩称为截面的扭矩，用T 表示之。 m
扭矩的正负号按右手螺旋法 则来确定，即右手握住杆的轴线，
Ⅰ
m
卷曲四指表示扭矩的转向，若拇
指沿截面外法线指向，扭矩为正， m 反之为负。
T
x
6
例1 画图示杆的扭矩图 3kN.m 1 5kN.m 2 2kN.m
3
（1）实际： 从有限元计算结果看剪切面上 应力的分布情况十分复杂，工 程中采用近似计算。
（2）假设：
切应力在剪切面上均匀分布；
V ＝ A
式中：A为剪切面的面积
V为剪切面上的剪力
（3）剪切时的强度条件 为保证构件不发生剪切破坏，要求剪切面上的平均剪应力 不超过材料的许用剪应力，即剪切时的强度条件为

02-剪切 -习题课

02-剪切 -习题课

第3章剪切3-1 计算题图示结构中销钉A 的许用切应力为 ，许用挤压应力为，试校核其强度。

[]MPa 80=τ[]MPa 170bs =σ200 10004080 40d =20（俯视图）b =80160F=10kNF AA ABC解：（1）计算约束力∑=0BMkN501055=⨯==F F A （2）销钉剪切强度校核销钉有两个剪切面，每个剪切面上的剪力为kN25502121S =⨯==A F F 剪切面面积为222S mm 16.314420π4π=⨯==d A 销钉剪切面上切应力为[]ττ<=⨯==MPa 6.7916.31410253S S A F 满足剪切强度要求3-1 计算题2001000408040d=20（俯视图）b=80160 F=10kNF AA AB C（3）销钉挤压强度校核销钉挤压力为kN50bs==AFF计算挤压面面积为2bsmm16002080=⨯==bdA销钉挤压应力为[]bs3bsbsbsMPa3.3116001050σσ<=⨯==AF满足挤压强度要求图(a)(b)所示螺栓连接接头，受拉力F 作用。

已知：F =100kN ，钢板厚δ=8mm ，宽b =100mm ，螺栓直径d =16mm 。

螺栓许用切应力[τ]=145MPa ，[σbs ]=340MPa ，钢板许用应力[σ]=170MPa 。

试校核该接头的强度。

δδbFFFF2211dFFF N1σσ{F N2{1122F SF S 2F S F S (a)(b)(d)(e)(c)F解（1）螺栓的剪切强度校核假定每个螺栓所受的剪力相同，如图(c)所示，则每个剪切面上的剪力为4S FF =每个剪切面上的切应力为[]ττ<=⨯⨯⨯=⨯==-MPa 4.1241016π101004π46232S S d F A F 螺栓满足剪切强度FF S 2F S F S(c)δδbFFFF2211dFFF N1σσ{F N2{1122F SF S 2F S F S (a)(b)(d)(e)(c)F（2）螺栓的挤压强度校核每个挤压面上的挤压力为 bs 4F F =每个挤压面上的切应力为[]3bs bs bs 6bs 10010195.3MPa 4416810F F A d σσδ*-⨯====<⨯⨯⨯⨯⨯螺栓满足挤压强度FF S 2F S F S(c)3-2 计算题FFFFF N1σσ{F N2{1122F S F S 2F S F S(d)(e)(c)F FF =N1()d b A -=δ1()()[]σδσ<=⨯-⨯⨯=-==-MPa 8.148101610081010063N1d b F A F （3）板的抗拉强度校核先沿第一排孔的中心线稍偏右将板截开，受力如图(d)所示，横截面1-1上正应力为3-2 计算题FσF N2{122F SF S 2F S F S(e)(c)FFF F F 434N2=-=()d b A 22-=δ()()[]σδσ<=⨯⨯-⨯⨯⨯⨯=-==-MPa 9.137101621008410100324/363N2d b F A F 再沿第二排孔的中心线稍偏右将板截开，受力如图(e)所示，截面2-2面积为截面2-2正应力为板满足抗拉强度。

材料力学课件：第3章 圆轴扭转时的应力变形分析与强度刚度计算计算

材料力学课件：第3章 圆轴扭转时的应力变形分析与强度刚度计算计算
韧性材料:不耐剪,最大剪应力所处截面是”最短木板”! 破坏方式是被剪断!
脆性材料:不耐拉,最大拉应力所处截面是”最短木板”! 破坏方式是被拉断!
承受扭转时圆轴的强度设计 与刚度设计
扭转强度设计
承受扭转时圆轴的强度设计 与刚度设计
扭转强度设计
与拉伸强度设计相类似，扭转强度设计时，首先需要根 据扭矩图和横截面的尺寸判断可能的危险截面；然后根据 危险截面上的应力分布确定危险点（即最大剪应力作用 点）；最后利用试验结果直接建立扭转时的强度设计准则。
承受扭转时圆轴的强度设计 与刚度设计
扭转实验与扭转破坏现象
韧性材料与脆性材料扭 转破坏时，其试样断口有着 明显的区别。韧性材料试样 最后沿横截面剪断，断口比 较光滑、平整。
铸铁试样扭转破坏时沿 45°螺旋面断开，断口呈细 小颗粒状。
经济学术语中的“木桶效应”，是说对于一个沿口 不齐的木桶而言，它盛水的多少并不在于木桶上那 块最长的木板，而在于木桶上最短的那块木板。
已知：钢制空心圆轴的外直径D＝100 mm，内直径d＝50 mm。若要求轴在2 m长度内的最大相对扭转角不超过1.5()，材 料的切变模量G＝80.4 GPa。
试： 1． 求该轴所能承受的最大扭矩； 2． 确定此时轴内最大剪应力。
解： 1．确定轴所能承受的最大扭矩 根据刚度设计准则，有
承受扭转时圆轴的强度设计 与刚度设计
＝
max
Mx WP
＝16M x πd13
＝16
1.5kN πd13
m
103
＝50.9
106
Pa
据此，实心轴的直径
d1＝3
16 1.5kN m 103＝53.1103 m＝53.1mm π 50.9 106 Pa

材料力学扭转详细讲解和题目非常好

材料力学扭转详细讲解和题目非常好

材料力学 扭转扭转的概念扭转是杆件变形的一种基本形式。

在工程实际中以扭转为主要变形的杆件也是比较多的，例如图6-1所示汽车方向盘的操纵杆，两端分别受到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用；图6-2所示为水轮机与发电机的连接主轴，两端分别受到由水作用于叶片的主动力偶和发电机的反力偶的作用；图6-3所示为机器中的传动轴，它也同样受主动力偶和反力偶的作用，使轴发生扭转变形。

图6—1 图6—2 图6—3这些实例的共同特点是：在杆件的两端作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶，使杆件的任意两个截面都发生绕杆件轴线的相对转动。

这种形式的变形称为扭转变形（见图6-4）。

以扭转变形为主的直杆件称为轴。

若杆件的截面为圆形的轴称为圆轴。

图6—4扭矩和扭矩图6.2.1 外力偶矩作用在轴上的外力偶矩，可以通过将外力向轴线简化得到，但是，在多数情况下，则是通过轴所传递的功率和轴的转速求得。

它们的关系式为 nP M 9550= （6-1） 其中：M ——外力偶矩（N ·m ）;P ——轴所传递的功率（KW ）；n ——轴的转速（r ／min ）。

外力偶的方向可根据下列原则确定：输入的力偶矩若为主动力矩则与轴的转动方向相同；输入的力偶矩若为被动力矩则与轴的转动方向相反。

6.2.2 扭矩圆轴在外力偶的作用下，其横截面上将产生连续分布内力。

根据截面法，这一分布内力应组成一作用在横截面内的合力偶，从而与作用在垂直于轴线平面内的外力偶相平衡。

由分布内力组成的合力偶的力偶矩，称为扭矩，用n M 表示。

扭矩的量纲和外力偶矩的量纲相同，均为N·m 或kN·m。

当作用在轴上的外力偶矩确定之后，应用截面法可以很方便地求得轴上的各横截面内的扭矩。

如图6-5（a ）所示的杆，在其两端有一对大小相等、转向相反，其矩为M 的外力偶作用。

为求杆任一截面m-m 的扭矩，可假想地将杆沿截面m-m 切开分成两段，考察其中任一部分的平衡，例如图6-5（b ）中所示的左端。

任务十三传动轴的扭转强度计算与变形验算

任务十三传动轴的扭转强度计算与变形验算

任务十三传动轴的扭转强度计算与变形验算任务十三传动轴的扭转强度计算与变形验算一、填空题1.根据平面假设,圆轴扭转变形后，横截面（仍保持为平面），其形状、大小与横截面间的距离（均不改变），而且半径（仍为直线）。

2.圆轴扭转时，根据（切应力互等定理），其纵截面上也存在切应力。

45螺旋面）。

3.铸铁圆轴受扭转破坏时，其断口形状为（与轴线约成0d D=的4. 一直径为1D的实心轴，另一内径为2d，外径为2D，内外径之比为220.8空心轴，若两轴的长度、材料、所受扭矩和单位长度扭转角均分别相同，则空心轴与W W=（ 0.47 ）。

实心轴的重量比215. 圆轴的极限扭矩是指(横截面上的切应力都达到屈服极限时圆轴所能承担的)扭矩。

对于理想弹塑性材料，等直圆轴的极限扭矩是刚开始出现塑性变形时扭矩的（4/3）倍。

6. 矩形截面杆扭转变形的主要特征是（横截面翘曲）。

二、选择题1.圆轴扭转时，若已知轴的直径为d,所受扭矩为T，试问轴内的最大剪应力τmax 和最大正应力σmax各为多大？（ A ）A．τmax=16T/πd3，σmax=0 B．τmax=32T/πd3，σmax=0C．τmax=16T/πd3，σmax=32T/πd3 D．τmax=16T/πd3，σmax=16T/πd32.扭转变形时，园轴横截面上的剪应力（ B ）分布。

A.均匀B.线性C.假设均匀D.抛物线3.扭转的受力特点是在杆两端垂直于杆轴的平面内，作用一对（ B ）。

A.等值、反向的力B.等值、反向的力偶C.等值、同向的力偶4.圆轴扭转时，最大的剪应力（ A ）。

A.在圆周处B.在圆心处C.在任意位置5.圆轴扭转时，（ B ）剪应力为零。

A.在圆周处B. 在圆心处C.在任意位置6.等截面空心园轴扭转时，园轴横截面上产生扭转最小剪应力发生在( D )处。

Ａ．外园周边 Ｂ.园心 Ｃ.截面任意点 Ｄ.内园周边7.扭转切应力公式ρτρPI T =适用于（ D ）A.任意截面B.任意实心截面C.任意材料的圆截面D.线弹性材料的圆截面8.单位长度扭转角θ与（ A ）无关。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

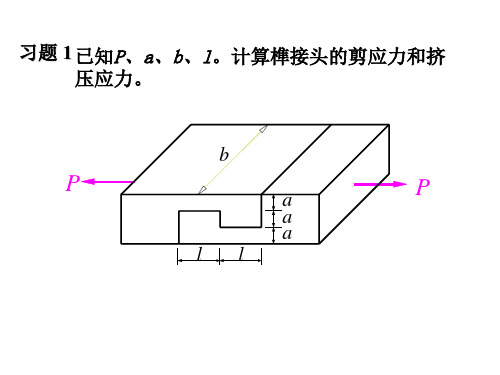
剪切扭转的内力与强度计算
一、填空题
图示铆接钢板用两个铆钉连接，钢板所受的力F = 10KN，则每个铆钉横截面上的剪力Q =_____ 。

图 1
二、判断题
1.图示两块钢块用四个铆钉对接，铆钉直径d相同，铆钉剪切面上剪应力大小为。

（）
图 2
2.穿过水平放置的平板上的圆孔，在其下端受有一拉力F，该插销的剪切
面积和挤压面积分别等于πdh，。

（）
3.图示木接头，左右两部分形状完全一样，当F作用时，接头的剪切面积等于ab,挤压面积等于cb。

（）
图3 图4
4.图示连接件，插销剪切面上的剪应力为τ=。

（）
图 5
5.剪应力的计算公式τ= 适用于任何受扭构件。

（）
6.圆轴的最大扭转剪应力τmax必发生在扭矩最大截面上。

（）
7.相对扭转角的计算公式φ= 适用于任何受扭构件。

（）
8.空心圆轴的内.外径分别为d和D，则其抗扭截面y数为。

（）
9.若实心圆轴的直径增大一倍，则最大扭转剪应力将下降为原来的1/16。

（）
10.一实心圆轴直径为d，受力如图所示，轴内最大剪应力为τmax=。

( )
图 6
11.轴扭转时,同一截面上各点的剪应力大小全相同。

（）
12.轴扭转时,横截面上同一圆周上各点的剪应力大小全相同。

（）
13.实心轴和空心轴的外径和长度相同时,抗扭截面模量大的是实心轴。

（）
三、选择题
1.剪切强度的实用计算的强度条件为（）
A.σ= N/A≤[σ]
B. τ=Q/A≤[τ]
C.σ= Pc/Ac≤[σc]
D. τmax=Mx/Wp≤[τ]
2.螺栓连接两块钢板，当其它条件不变时，螺栓的直径增加一倍，挤压应力将减少（）倍。

A．1 B．1/2 C．1/4 D．3/4
3.图示扭转轴1——1截面上的扭矩Mx为（）
A． Mx =–2KN·m
B．Mx = 5 KN·m
C．Mx = 1 KN·m
D．Mx = 4 KN·m
图 7
4.圆轴扭转时，横截面上同一圆周上各点的剪应力大小应是（）
A．全不同 B．全相同 C．部分相同 D．无法比较
四、分析题
1.在校核受扭圆轴的刚度时，发现原设计是扭转角超过了许用扭转角。

现有两种修改方案：①改用优质材料；②加大圆轴直径。

你选择方案，为什么？因为。

2.单位扭转角的计算公式是什么？
3.直径相同，材料不同的两根等长的实心圆轴，在相同的扭矩作用下，其
是否相同。

4.在校核受扭圆轴的刚度时，发现原设计是扭转角超过了许用扭转角。

现
有两种修改方案：①改用优质材料；②加大圆轴直径。

你选择方案，为什么？因为。

5.单位扭转角的计算公式是什么？
6.直径相同，材料不同的两根等长的实心圆轴，在相同的扭矩作用下，其
是否相同。

五、计算题
1.实心圆轴受力如图示,已知直径d=20mm,试绘扭矩图,并求轴内最大剪应力.
图 8
２.图9所示圆轴直径d=60mm,长L=1m,转矩M=5KN·m,材料的剪切弹性模量Mpa试求：
〈1〉截面上a,b,c三点的剪应力值，并在图上画出其方向；〈2〉最大剪应力及单位扭转角。

图 9
3.圆轴尺寸及载荷如图10所示。

已知：材料简切弹性摸量
试校核该轴强度和刚度。

图10
4.一传动轴受力情况如图所示。

已知材料的许用剪应力[τ]=40MPa，许用扭转角,材料的剪切弹性模量。

(a) 试设计轴的直径。

(b) 已知轴的直径为60mm，试校核轴的强度和刚度。

图 11
5.一空心圆轴外径D=100mm，内径d=50mm，两端受外力偶矩Mx=1000N·m ，求截面上的最大剪应力，最小剪应力，并绘出截面剪应力分布图。