强度理论典型习题解析
- 格式:pdf
- 大小:261.15 KB
- 文档页数:8


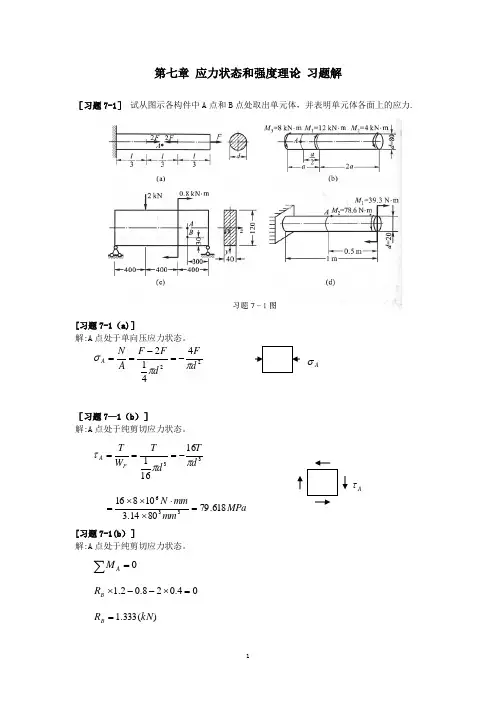
工程力学(工程静力学与材料力学)习题与解答第12章 强度理论12-1 对于建立材料在一般应力状态下的失效判据与设计准则,试选择如下合适的论述。
(A )逐一进行试验,确定极限应力;(B )无需进行试验,只需关于失效原因的假说;(C )需要进行某些试验,无需关于失效原因的假说; (D )假设失效的共同原因,根据简单试验结果。
知识点:建立强度理论的主要思路 难度:一般 解答:正确答案是 D 。
12-2 对于图示的应力状态(y x σσ>)若为脆性材料,试分析失效可能发生在: (A )平行于x 轴的平面; (B )平行于z 轴的平面;(C )平行于Oyz 坐标面的平面; (D )平行于Oxy 坐标面的平面。
知识点:脆性材料、脆性断裂、断裂原因 难度:难 解答:正确答案是 C 。
12-3 对于图示的应力状态,若x y σσ=,且为韧性材料,试根据最大切应力准则,失效可能发生在: (A )平行于y 轴、其法线与x 轴的夹角为45°的平面,或平行于x 轴、其法线与y 轴的夹角为45°的平面内;(B )仅为平行于y 轴、法线与z 轴的夹角为45°的平面; (C )仅为平行于z 轴、其法线与x 轴的夹角为45°的平面; (D )仅为平行于x 轴、其法线与y 轴的夹角为45°的平面。
知识点:韧性材料、塑性屈服、屈服原因 难度:难 解答:正确答案是 A 。
12-4 铸铁处于图示应力状态下,试分析最容易失效的是: (A )仅图c ; (B )图a 和图b ; (C )图a 、b 和图c ; (D )图a 、b 、c 和图d 。
知识点:脆性材料、脆性断裂、断裂准则 难度:一般 解答:正确答案是 C 。
12-5低碳钢处于图示应力状态下,若根据最大切应力准则, 试分析最容易失效的是: (A )仅图d ; (B )仅图c ; (C )图c 和图d ; (D )图a 、b 和图d 。

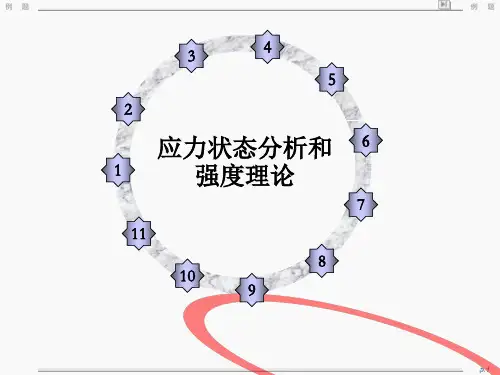
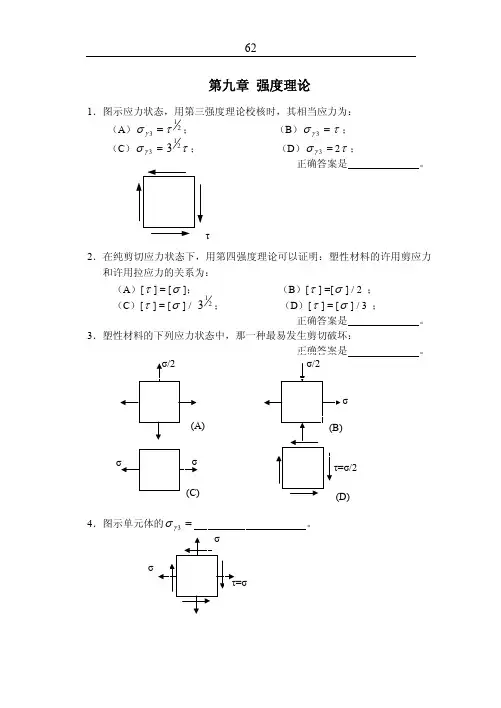
第九章 强度理论1.图示应力状态,用第三强度理论校核时,其相当应力为:(A )213τσγ=; (B )=3γστ;(C )=3γστ213; (D )=3γσ2τ;正确答案是 。
2和许用拉应力的关系为:(A )[τ] = [σ]; (B )[τ] =[σ] / 2 ;(C )[τ] = [σ] / 213; (D )[τ] = [σ] / 3 ;正确答案是 。
3.塑性材料的下列应力状态中,那一种最易发生剪切破坏:45.第三强度理论和第四强度理论的相当应力分别为3γσ 及4γσ ,对于纯剪应力状态,恒有3γσ / 4γσ= 。
6.按第三强度理论计算图示单元体的相当应力3γσ= 。
7.图示①、②、③为三个平面应力状态的应力圆,试画出各应力圆所对应的主平面微元体上的应力。
8.图示为承受气体压力p 的封闭薄壁圆筒,平均直径为D ,壁厚t ,气体压强p 均为已知,用第三强度理论校核筒壁强度的相当应力3γσ= 。
9.单元体如图,已知αττσ42−==xy y 。
证明:2/3/=y x σσ ;6/7/=x σσα。
τx10.证明线弹性材料的泊松比μ满足关系式:0<μ<0.511.图(a )、(b )表示同一材料的两个单元体。
材料的屈服极限s σ= 275 MPa 。
试根据第三强度理论求两个单元体同时进入屈服极限时拉应力σ 与剪应力τ的值。
若σ> τ。
(a) (b)12.图示受扭圆轴的d = 30 mm ,材料的弹性模量 ,v =0.3 ,屈服极限MPa E 5101.2×=S σ= 240MPa ,实验测得a b 方向的应变为 0002.0=ε 。
试按第三强度理论确定设计该轴时采用的安全系数。
13.从低碳钢零件中某点处取出一单元体,其应力状态如图所示,试按第三、四强度理论计算单元体的相当应力。
单元体上的应力为60=ασ,80−=βσ,(°+=90αβ),40−=ατ (单位:MPa 。

德州学院,材料⼒学,期末试题7章习题讲解第七章⼒和应变分析强度理论 §7.1应⼒状态概述1.过受⼒构件内⼀点,取截⾯的不同⽅位,这⼀点在各个⾯上的(D ). (A )正应⼒相同,切应⼒不同;(B )正应⼒不同,切应⼒相同;(C )正应⼒和切应⼒都相同;(D )正应⼒和切应⼒都不同。
2.关于单元体的描述,下列正确的是A(A )单元体的三维尺⼨必须是微⼩的;(B )单元体是平⾏六⾯体;(C )单元体必须是正⽅体;。
(D )单元体必须有⼀对横截⾯。
3.对于图⽰承受轴向拉伸的锥形杆上的A 点,哪⼀种应⼒状态是正确的Dxτxx4.在单元体的主平⾯上()。
(A )正应⼒⼀定最⼤;(B )正应⼒⼀定为零;(C)切应⼒⼀定最⼩;(D )切应⼒⼀定为零。
§7.2⼆向应⼒状态实例1. Q235钢制成的薄壁圆筒形蒸汽锅炉,壁厚δ,内径D ,蒸汽压⼒p ,试计算锅炉壁内任意⼀点处的三个主应⼒。
注:薄壁圆筒受⼒均匀,因此,任意点的应⼒状态均相同。
1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz 薄壁圆筒与纸⾯垂直⽅向上的σz 为零.总结:薄壁圆筒的三个主应⼒为:薄壁圆筒为两向应⼒状态注意事项:1.注意单位配套使⽤;2. 纵向截⾯上正应⼒是横截⾯正应⼒的两倍;3.按规定排列正应⼒。
课本215页例7.1如下由Q235钢制成的蒸汽锅炉,壁厚δ=10mm,内径D=1m,蒸汽压⼒p=3MPa,试计算锅炉壁内任意⼀点处的三个主应⼒。
经分析,薄壁圆筒为两向应⼒状态2. 圆球形容器的壁厚为δ,内径为D,内压为p,求容器内任意⼀点的应⼒。
注:薄壁圆球受⼒均匀,因此,任意点的应⼒状态均相同。
1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz薄壁圆筒与纸⾯垂直⽅向上的σz为零.球形薄壁容器的三个主应⼒为:受内压的球形薄壁容器为⼆向应⼒状态§7.3 ⼆向应⼒状态分析——解析法⼆向应⼒状态下,单元体各⾯上应⼒分量皆为已知,如下图所⽰:求垂直于xy平⾯的任意斜截⾯ef上的应⼒及主应⼒和主平⾯⼀.符号规定1.正应⼒正负号规定2.切应⼒正负号规定使微元或其局部顺时针⽅向转动为正;反之为负。

第8章作业参考解答本章主要公式:五种强度理论的强度条件统一形式: σr ≤[σ]式中σr 称为相当应力 (equivalent stress), 五种强度理论的相当应力分别为: 第一强度理论:11s s =r第二强度理论:)(3212s s n s s +-=r 第三强度理论:313s s s -= 第四强度理论:=4r s ])()()[(21213232221s s s s s s -+-+- 莫尔强度理论:31][][s s s s s c t rM -=8-3 炮筒横截面如图所示。
在危险点处,σt =60MPa ,σr =-35MPa ,第三主应力垂直于纸面为拉应力,其大小为40MPa ,试按第三和第四强度论计算其相当应力。
解:第三强度理论相当应力313r s s s =-第四强度理论相当应力4r s =这里160MPa s =,240MPa s =,335MPa s =- 故31395MPa r s s s =-=486.75MPa r s ==8-6 已知钢轨与火车车轮接触点处的正应力σ1=-650MPa ,σ2=-700MPa ,σ3=-900MPa 。
如钢轨的容许应力[σ]=250MPa ,试用第三强度理论和第四强度理论校核该点的强度。
解:第三强度理论相当应力313r s s s =-第四强度理论相当应力4r s =这里1650MPa s =-,2700MPa s =-,3900MPa s =- 故313250MPa=[]r s s s s =-=4229MPa<[]r s s == 所以该点满足强度要求。
8-7 受内压力作用的容器,其圆筒部分任意一点A 处的应力状态如图(b)所示。
当容器承受最大的内压力时,用应变计测得:εx =1.88×10-4,εy =7.37×10-4。
已知钢材弹性模量E =2.1×105MPa ,横向变形系数v =0.3,[ σ]=170MPa 。

10-4 求图示应力状态的第三、四强度理论的相当应力。
解:(1)由单元体可知:z 面为主面60MPa z σ=。
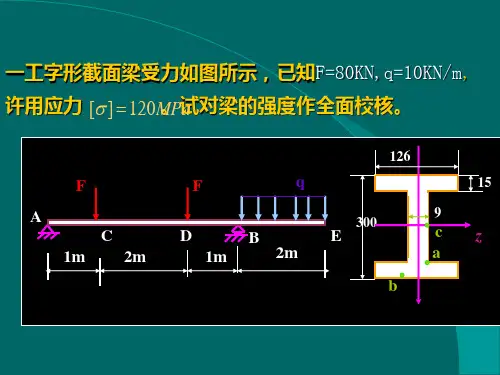
100MPa =15MPa =-20MPa x x y στσ=,, (3) 求梁的主应力及主平面方位角:max min 1002022101.854061.85()21.85x y MPa σσσσ+⎫-=±=±⎬⎭⎧=±=⎨-⎩故,123101.85MPa,60MPa,21.85MPa σσσ===-(2)第三强度理论相当应力313101.85(21.85)123.7MPa r σσσ=-=--=(3)第四强度理论相当应力4108.98MPa r σ===10-7图示简支梁为焊接工字钢,(1)试校核梁内的最大正应力和。
(2)试校核最大剪应力强度。
(3)试分别用第三、第四强度理论校核钢梁的强度。
M kN ·m)64+V kN)(c )(b)解:(1)外力分析,判变形:求支反力Y A =160kN (↑), Y B =40 kN (↑)梁发生平面弯曲,中性轴过形心沿水平方向。
(2)内力分析及应力分析,画内力图如图所示。
①剪应力强度危险面于梁的左段各横截面,V max =160kN ,危险面的中性轴上各点是剪应力强度的危险点。
②正应力强度危险面于集中力处截面max 64M =⋅kN m ,跨中截面的上下边缘点是正应力强度的危险点。
③按第三、四强度理论,集中力处C 的左截面也可能是危险面,C 的左截面腹板和翼板的交界处为强度理论的危险点。
(3)求截面的几何性质:336512030055.5270287.9108.79101212z I -⨯⨯=-⨯=⨯=⨯44mm m4,30012015(7.5)256500 2.565102z a S *-=⨯⨯-==⨯33mm m 4,30013512015(7.5)1359338512.5 3.3851022z S *-=⨯⨯-+⨯⨯==⨯半33mm m m mm 135.0135==a y(4)对梁进行正应力校核[]3max max 564100.150109.21608.7910b zM y I σσ-⨯=⋅=⨯==⨯Pa MPa <MPa故,满足正应力强度。
材料力学B试题7应力状态-强度理论LT应力状态 强度理论1. 图示单元体,试求(1) 指定斜截面上的应力;(2) 主应力大小及主平面位置,并将主平面标在单元体上。
解:(1)MPa6.762sin 2cos 22=--++=ατασσσσσαx yx yxMPa 7.322cos 2sin 2-=+-=ατασσταx yx(2)22min max )2(2xy y x y x τσσσσσσ+-±+=98.12198.81-=MPa 98.811=σMPa ,02=σ,98.1213-=σ35.3940200arctan 21)2arctan(210==--=yx xyσστα2.解:取合适坐标轴令25=x σ MPa ,9.129-=xτ由02cos 2sin 2120=+-=ατασστxy yx得125-=yσMPa所以22min max )2(2xy y x y x τσσσσσσ+-±+=20010015050)9.129(755022-=±-=-+±-= MPa1001=σMPa ,02=σ,2003-=σ MPa3. 一点处两个互成 45平面上的应力如图所示,其中σ未知,求该点主应力。
解:150=yσMPa ,120-=x τ MPaMPa由 ατασστ2cos 2sin 245xy yx +-=802150-=-=x σ得10-=x σ MPa所以22min max )2(2xyy x y x τσσσσσσ+-±+=22.7422.214-= MPa22.2141=σ MPa ,02=σ,22.743-=σ4. 图示封闭薄壁圆筒,内径100=d mm ,壁厚2=t mm ,承受内压4=p MPa ,外力偶矩192.0=e MkN ·m 。
求靠圆筒内壁任一点处的主应力。
解:75.505.032)1.0104.0(π10192.0443=⨯-⨯=x τ MPa504==t pd x σ MPa1002==tpd y σ MPa35.497.100)2(222min max =+-±+=xy y x y xτσσσσσσ MPa7.1001=σ MPa ,35.492=σ MPa ,43-=σ MPa5. 受力体某点平面上的应力如图示,求其主应力大小。
一. 是非题:正确的在()中写“√”,错误的在()中写“×”1、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,将会降低该零件的冲击强度。
( )2、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,可提高耐冲击强度。
( )3、设计零件时,安全系数应尽可能选大些,使该零件工作更可靠与安全。
( )4、某转轴采用40钢(σS MPa =335),经校核其扭转刚度不够,可改选高强度合金结构钢40Cr ()σS MPa =785,以提高刚度。
( )5、设计某普通碳钢零件时,校核后刚度不足,采用高强度合金钢时,对提高其刚度是不起作用的。
( )6、在变应力作用下,零件的主要失效形式将是疲劳断裂,而在静应力作用下,其失效形式将是塑性变形或断裂。
( )7、只要材料的平均极限应力σlim 大于零件的平均工作应力σm ,则安全系数S 就大于1,工作是可靠的。
( )8、若材料的平均极限应力σlim 大于零件的平均工作应力σm ,则零件的安全系数不一定总是大于1。
( )9、渐开线圆柱直齿轮传动空载运转时,可以认为是处于齿面线接触状态。
( )10、渐开线圆柱直齿轮传动工作时,齿面载荷的传递是通过真实的线接触进行的。
( )11、两圆柱体相接触,其轴线互相平行,在受法向压力作用下,则两零件的接触应力不等,直径大的零件所受接触应力小。
( )12、两圆柱体相接触,其轴线互相平行,受法向压力,则两零件的接触应力相等。
( )二、选择题:把正确的选项代号填入()中1、在受轴向变载荷的紧螺栓联接中,采用柔性螺栓,是为了_____________。
A.增大变载荷下的剩余预紧力,提高联接可靠性;B.改善变载荷下的螺母支承面接触状态;C.降低应力幅σa;D.可减轻螺栓重量,节省材料。
2、已知某转轴在复合应力状态下工作,其弯矩作用与扭矩作用下的安全系数分别为Sσ=6.1,Sτ=18.5,则该转轴的实际安全系数大小为_____________________。
强度理论典型习题解析1 已知铸铁的拉伸许用应力MPa 30][t =σ,压缩许用应力MPa 90][c =σ,30.0=µ,试对铸铁零件进行强度校核,危险点的主应力为:(1) MPa 301=σ,MPa 202=σ,MPa 153=σ; (2) MPa 201−=σ,MPa 302−=σ,MPa 403−=σ; (3) MPa 101=σ,MPa 202−=σ,MPa 303−=σ。
解题分析:选用强度理论时,不但要考虑材料是脆性或是塑性,还要考虑危险点处的应力状态。
解:(1) MPa 301=σ,MPa 202=σ,MPa 153=σ,危险点处于三向拉应力状态,不论材料本身是塑性材料或是脆性材料,均采用第一强度理论,即:][0MPa 3t 1r1σσσ===,安全(2) MPa 201−=σ,MPa 302−=σ,MPa 403−=σ,危险点处于三向压应力状态,即使是脆性材料,也应采用第三或第四强度理论,即:][MPa 20)MPa 40(MPa 20t 31r3σσσσ<=−−−=−=,安全 ])MPa 20MPa 40()MPa 40MPa 30()MPa 30MPa 20[(21222r4+−++−++−=σ, ][MPa 3.17t σ<=,安全。
(3) MPa 101=σ,MPa 202−=σ,MPa 303−=σ,脆性材料的危险点处于以压应力为主的应力状态,且许用拉应力与许用压应力不等,宜采用莫尔强度理论,即:][MPa 02MPa)30(MPa90MPa30MPa 10][][t 3c t 1rM σσσσσσ<=−−=⋅−=,安全 2 图示实心圆轴受轴向外力F 和外力偶M 作用。
已知圆轴直径d =10 mm ,M =Fd /10。
(1)材料为钢时,许用应力MPa 160][=σ;材料为铸铁时,许用应力MPa 30][t =σ。
试分别计算圆轴的许可载荷;(2)材料为铸铁,且F =2 kN 、E =100 GPa 、][F 25.0=µ,计算圆轴表面上与轴线成30°方位上的正应变。
题2图解题分析:本题中,轴为拉伸和扭转组合变形。
轴的各个横截面上的扭矩、轴力均相同,所以可以任取一截面作为危险截面。
在危险截面上,轴力引起的拉伸正应力处处相等,扭矩引起的切应力在靠近轴外表面的各点处最大,所以危险点为靠近轴表面的各点。
危险点处的应力状态如图示。
解:1、计算危险点的主应力轴力引起的正应力 F dFA F 242N m 1027.1π4−×===σ 扭矩引起的切应力 F dFd W MW T 243p p m 10509.010π16−×====τ 危险点处的极值应力为22422424minmax)m 10509.0()2m 1027.1(2m 1027.1F F F −−−×+×±×=σ于是主应力为 ,F 241m 1045.1−×=σ02=σ, F 243m 10179.0−×−=σ2、材料为钢材时,确定轴的许用载荷根据第三强度理论,有MPa 160][m 1063.1m 10179.0m 1045.124242431r3=≤×=×+×=−=−−−σσσσF F F 得 kN 9.82N 9820m 101.63MPa160][24==×=−F该轴用钢材制造时,许可载荷kN 9.82][=F 3、材料为铸铁时,确定轴的许可载荷按第一强度理论,有MPa 30][m 1045.1t 241r1=≤×==−σσσF得许可载荷kN 2][=F 4、计算铸铁轴表面与轴线成30°方位上的正应变根据广义胡克定律公式,要计算与轴线成30°方位上的正应变,必须知道该方向的正应力和与该方向垂直的方向上的正应力。
设要计算的方位为-30°,则与其垂直的方位为60°,首先计算-30°、60°两方位上的正应力。
与轴线平行方向上的正应力、切应力分别为MPa 4.25N 102m 1027.1m 1027.132424=×××=×=−−F σMPa 18.10N 102m 100509.0m 10509.032424=×××=×=−−F τ于是MPa87.27)]30(2sin[18.10)]30(2cos[2MPa 4.252MPa 4.25)]30(2sin[)]30(2cos[2230=−×−−×+=−×−−×+=−D D D D D τσσσMPa47.2)602sin(MPa 18.10)602cos(2MPa 4.252MPa 4.25)602sin()602cos(2260−=×−×+=×−×+=D D D D D τσσσ由广义胡克定律,轴表面与轴线成30°方位上的正应变为6360303010285MPa))47.2(25.0MPa 87.27(MPa101001)(1−−−×=−×−×=−=D D D µσσεE 讨论:该题中正应变的计算也可以用公式αγαεεεεεα2sin 22cos 22xy yx yx −−++=,但和上面方法相比,要麻烦得多。
3 图示钢轴有两个皮带轮A 和B ,两轮的直径D =1m ,轮的自重Q =5kN ,轴的许用应力MPa 80][=σ。
试确定轴的直径d 。
解题分析:本题轮轴为弯扭组合变形。
首先要将所有外力向轴线上简化,并绘制内力图,以便寻找危险截面。
找到危险截面和危险点后,即可按强度条件设计轴直径。
解: 1、计算轴上的载荷取如图示坐标系,则外力偶矩mkN 1.521mkN 2)-(52kN2)-(5e e ⋅=×===DM M B Axy 平面支反力 F Cy =12.5 kN , F Dy =4.5 kN xz 平面支反力 F Cz =9.1 kN ,F Dz =2.1 kN 2、画内力图,确定危险截面轴AB 段的扭矩为(图c ),弯矩和如图d 、e 所示。
从内力图看出,危险截面是C 或B 截面。
分别计算C 、B 两截面的总弯矩:m kN 1.5⋅=T y M z M mkN 58.2m N 1058.2m)N 105.1(m)N 101.2(32323⋅=⋅×=⋅×+⋅×=C M mkN 49.2m N 1049.2m)N 1025.2(m)N 1005.1(32323⋅=⋅×=⋅×+⋅×=B M 比较两者大小,可知危险截面为C 截面。
3、确定轴的直径按第三强度理论设计轴的直径。
直接采用圆轴弯扭组合情况下的强度条件,得][22r3σσ≤+=WT Mmm4.72m 104.72Pa1080πm)N 105.1(m)N 1058.2(32][π323623233223=×=××⋅×+⋅×=+≥−σT M d 如果按第四强度理论设计轴的直径,则][75.022r4σσ≤+=WT Mmm6.71m 106.71Pa1080πm)N 105.1(75.0m)N 1058.2(32][π75.0323623233223=×=××⋅××+⋅×=+≥−σT M d比较可得按第三强度理论设计的轴径比按第四强度理论设计的轴径略大。
4 一端固定的轴线为半圆形的正方形截面杆,受力情况如图,F =1000N ,试求B 和C 截面上危险点处的相当应力r3σ。
解题分析:本题为非圆截面弯扭组合变形问题。
首先应找出B 和C 截面的危险点,并确定危险点处的应力状态,然后计算相当应力。
解: 1、计算截面有关的几何性质杆的横截面面积262m 10900mm 900mm 30mm 30−×==×==bh A 1.5 kN·m题3图Mz 2.25kN·m1.05 kN·m(c)My2.1 kN·m(b)(a)(d)(e)抗弯截面系数 39322m 104500mm 45006mm)30(mm 306−×==×==bh W1mm 30mm/30/==b h ,查表 208.0=β抗扭截面系数 p m 105620mm 5620mm 30(8−×==×=W 2内力 39333)20.0=b β、计算B 截面的剪力 1000N S ==F F弯矩 m 200N 0.2m 1000N ⋅=×==FR M 扭矩 m 200N 0.2m 1000N ⋅=×==FR TB 截面的危险点及危险点处的应力状态(图b )cd 各点,顶边受拉应力,底3、确定截面上弯矩引起的最大正应力发生在截面顶边ab 和底边边受压应力,大小为MPa .444Pa 104.44m 104500m N 200==M σ639=×=×⋅−W 最大弯曲切应力发生在截面中性轴h f 线上各点,方向向下,大小为1.67MPa Pa 101.67N100033626S 1=×=×==−F τ m1090022×A 扭转引起的最大切应力发生在截面四边中点e 、f 、g 、h 处,方向平行于所在边,且e 点处方向向右、f 点处向下、g 点处向左、h 点处向上。
扭转切应力大小均为35.6MPa Pa 106.53m N 2006392=×=⋅==−T τ m105620p ×W 考虑弯曲切应力、弯曲正应力和扭转切应力共同作用,e 点处为单向拉伸应力状态如图c 所示,MPa .444=σ,MPa 35.62==ττ。
g 点处应力状态与e 点处类似,只是正应力为压应力纯剪应力大小为MPa 3.73MPa 6.35MPa 67.121。
f 点处为切应力状态,切=+=+=τττ题4图)(c) e 点应力状态 (a)(d) C 截面(y -y 方向视图)h 点处应力状态也为纯剪切,切应力大小为MPa 93.33MPa 67.1-MPa 6.3512==−=τττ。
比较四点处的应力状态,可知e 点为B 截面的危险点。
按第三强度理论计算其相当应力为MPa 9.83MPa)6.35(4MPa)4.44(42222r3=×+=+=τσσ4、计算C 截面上内力和应力 剪力 ==F F =0扭矩1000N S 弯矩 M 2m 400N 0.2m 1000N 2⋅=××=FR 5、计算截面危险点的应力(图d )C 截面轴内侧中点,即图d 中值为=T C C 截面各点处均为纯剪切应力状态,最大切应力发生在f 点处,其MPa9.72Pa 109.72)m1030208.0m 10200223(m)1030(N1000223(22323S max =F τ6332322p =×=××××+×=+=+=+−−−bR b F b FR A F W TA ββ按第三强度理论计算相当应力145.8MPa MPa 9.7222442max 22r3=+=ττσσmax =×==τ5 图示薄壁容器承受内压p 。