八年级数学勾股定理与平方根测试卷

第二章勾股定理与平方根单元测评卷（A）（附答案）（满分：100分时间：60分钟）一、选择题（每题4分，共28分）1．一个直角三角形的两边长分别为6 cm、8 cm，则这个三角形的斜边长为( )A．8 cm B．10 cm C．8 cm或10 cm D．10 cm或cm2．若等腰三角形中相等的两边长为10 cm，第三边长为16 cm，则第三边上的高为( ) A．6 cm B．8 cm C．10 cm D．12 cm3．若三角形的三边长分别为10、24、26，则它最长边上的中线长是( ) A．10 B．11 C．13 D．344．（2010．阜新）国家游泳中心——“水立方”是2008年北京奥运会标志性建筑物之一，其工程占地面积为62 828平方米，将62 828用科学记数法表示是（结果保留3个有效数字）( )A．6.28×103B．6.28×104C．6.282 8×l04D．0.628 28×1055( )A．5个B．4个C．3个D．2个6．如图，在四边形ABCD中，AB＝3 cm，BC＝4 cm，CD＝12 cm，DA＝13 cm，且∠ABC ＝90°，则四边形ABCD的面积是( )A．84 cm2B．36 cm2C．25.5 cm2D．无法确定7．如图，在由16个边长为1的小正方形拼成的图案中，有五条线段PA、PB、PC、PD、PE，其中长度是无理数的有( )A．1条B．2条C．3条D．4条二、填空题（每题4分，共28分）8．－4的绝对值是_______ ．81的平方根是______．9．如图，在数轴上点A和点B之间表示整数的点有_______个．10．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm，则A、B．C、D四个正方形的面积之和是______cm2．11．上海世博会的中国建筑外观以“东方之冠，鼎盛中华，天下粮仓，富庶百姓”为构思主题，建筑面积为4. 645 7万平方米，4.645 7保留2个有效数字是______万平方米．12．已知实数a 、b 10b -=，则a 2012＋b 2011＝______．13．如图，A 村到公路l 的距离AB ＝2 km ，C 村到公路l 的距离CD ＝6 km ，且BD ＝6 km现要在公路l 上取一点P ，使AP ＋CP 的值最小，则这个最小值为______．14．如图，△ABC 是直角边长为1的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，……依此类推，第n 个等腰直角三角形的斜边长是______．三、解答题（共44分）15．（6分）把下列各数填入相应的集合内：－6，0.45，0，2273π- 有理数集合：{ …}；无理数集合：{ …}．16．（6分）求下面各式中x 的值．(1)8－2(x －1)2＝－10；30-．17．（7分）如图，正方形网格中每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下面的要求画三角形．(1)在图①中画一个三角形，使它的三边长都是有理数；(2)在图②、图③中分别画一个直角三角形，使它们的三边长都是无理数，且所画的两个三角形不全等．18．（7分）如图，为了求出湖两岸的A、B两点之间的距离，一个观测者在点C设桩，使△ABC恰好为直角三角形，且∠ABC＝90°．通过测量，得到AC长为160米，BC长为128米．问从点A穿过湖到点B有多远？19．（9分）《中华人民共和国道路交通管理条例》规定：小汽车在城市街路上的行驶速度不得超过70 km/h．如图，一辆小汽车在一条城市街路上沿直道CB行驶，某一时刻刚好行驶到路对面车速检测仪A点正前方30 m的C点处，过了2s后，测得小汽车与车速检测仪之间的距离AB＝50 m．这辆小汽车超速了吗？20．（9分）如图，折叠长方形的一边AD，使点D落在BC边上的点F处．如果AB＝8 cm，BC＝10 cm，求EC的长．参考答案一、1．C 2．A 3．C 4．B 5．A 6．B 7．C二、8．4 ±9 9．4 10． 49 11．4.6 12．2 13．10 km 14．n三、 15．－6，0.45， 0，227 3π-16．(1)x ＝4或x ＝－2 (2)x ＝5或x ＝117．答案不惟一，(1)如图①所示 (2)如图②、③所示18．从点A 穿过湖到点B 有96米 19．这辆小汽车超速了20．EC 的长为3。

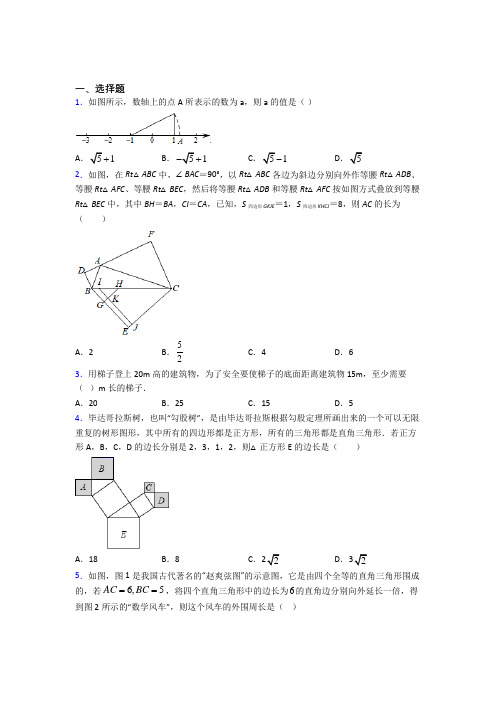
一、选择题1．如图所示，数轴上的点A 所表示的数为a ，则a 的值是（ ）A ．51+B ．51-+C ．51-D ．52．如图，在Rt △ABC 中，∠BAC ＝90°，以Rt △ABC 各边为斜边分别向外作等腰Rt △ADB 、等腰Rt △AFC 、等腰Rt △BEC ，然后将等腰Rt △ADB 和等腰Rt △AFC 按如图方式叠放到等腰Rt △BEC 中，其中BH ＝BA ，CI ＝CA ，已知，S 四边形GKJE ＝1，S 四边形KHCJ ＝8，则AC 的长为（ ）A ．2B ．52C ．4D ．63．用梯子登上20m 高的建筑物，为了安全要使梯子的底面距离建筑物15m ，至少需要（ ）m 长的梯子．A ．20B ．25C ．15D ．54．毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A ，B ，C ，D 的边长分别是2，3，1，2，则△正方形E 的边长是（ ）A ．18B ．8C ．2D ．2 5．如图，图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若6,5AC BC ==，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（ ）A ．24B ．52C ．61D ．766．如图所示的图案是由两个直角三角形和三个正方形组成的图形，其中一直角三角形的斜边和一直角边长分别是13，12，则阴影部分的面积是（ ）A ．25B ．16C ．50D ．417．如图，在Rt △ABC 中，∠ACB ＝90°，AB ＝10，AC ＝8，AB 的垂直平分线DE 交BC 的延长线于点E ，则DE 的长为（ ）A ．103B ．256C ．203D ．1548．已知Rt ABC 中，A ∠，B ，C ∠的对边分别为a 、b 、c ，若90B ∠=︒，则（ ）．A ．222b a c =+B ．222c a b =+C ．222a b c =+D ．a b c +=9．《九章算术》是我国古代最重要的数学著作之一，它的出现标志着中国古代数学形成了完整的体系．“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈，末折抵地，去本四尺，问折者高几何？”翻译成数学问题是：如图所示，ABC 中，90ACB ∠=︒，10AC AB +=尺，4BC =尺，求AC 的长．则AC 的长为（ ）A ．4.2尺B ．4.3尺C ．4.4尺D ．4.5尺 10．如图，分别以直角三角形ABC 的三边为斜边向外作直角三角形，且AD CD =，CE BE =，AF BF =，这三个直角三角形的面积分别为1S ，2S ，3S ，且19S =，216S =，则S 3S =（ ）A ．25B ．32C ．7D ．1811．在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地 送行二步与人齐，五尺人高曾记． 仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几．”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离AB 长度为1尺．将它往前水平推送10尺时，即A C '＝10尺，则此时秋千的踏板离地距离A D '就和身高5尺的人一样高．若运动过程中秋千的绳索始终拉得很直，则绳索OA 长为（ ）A ．13.5尺B ．14尺C ．14.5尺D ．15尺 12．若实数m 、n 满足340m n --=，且m 、n 恰好是Rt ABC △的两条边长，则第三条边长为（ ）．A ．5B 7C ．57D ．以上都不对二、填空题13．将五个边长为2的正方形按如图所示放置，若A ，B ，C ，D 四点恰好在圆上，则这个圆的面积为________．（结果保留π）14．如图，一只蚂蚁从长、宽都是2，高是5的长方体纸盒的A 点沿纸盒面爬到B 点，那么它所行的最短路线的长是________.15．在△ABC 中，AB=10，AC=210，BC 边上的高AD=6，则另一边BC 等______． 16．公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾6a =，弦10c =，则小正方形ABCD 的面积是____.17．在平面直角坐标系中，若点M （2，4）与点N （x ，4）之间的距离是3，则x 的值是_____．18．如图，两个正方形的面积分别是118S =，212S =，则第三个正方形的面积3S =_________．19．如图，一个蚂蚁要在一个长、宽、高分别为2、3、1分米的长方体的表面从A 点爬到B 点，那么最短的路径是_______________分米．（结果保留根号）20．如图，ABC 中，90C ∠=︒，D 是BC 边上一点，17AB cm =，10AD cm =，8AC cm =，则BD 的长为________.三、解答题21．如图，ABC 中，∠C=90°，BC=5厘米，AB=55厘米，点P 从点A 出发沿AC 边以2厘米/秒的速度向终点C 匀速移动，同时，点Q 从点C 出发沿CB 边以1厘米/秒的速度向终点B 匀速移动，P 、Q 两点运动几秒时，P 、Q 两点间的距离是210厘米？22．已知：如图，四边形ABCD 中，AB ⊥BC ，AB=3，BC=4，CD=12，AD=13，求四边形ABCD 的面积．23．如图，一棵小树在大风中被吹歪，用一根棍子把小树扶直，已知支撑点到地面的距离10 5.5米，求棍子和地面接触点C 到小树底部B 的距离是多少?24．在如图所示的方格纸中，每个小正方形的边长为1个单位长度，我们称每个小正方形的顶点为“格点”．（1）若格点C 在线段AB 右侧，且满足AC BC =，则当ABC ∆的周长最小时，ABC ∆的面积等于 ．（2）若格点D 在线段AB 左侧，且满足AD BD ⊥，则ABD ∆的面积等于 (以上两问均直接写出结果即可）．25．如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若6AC =，5BC =，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，求这个风车的外围周长．26．如图，在四边形ABCD 中， 45,ABC ADC ∠=∠=︒将BCD 绕点C 顺时针旋转一定角度后，点B 的对应点恰好与点A 重合，得到ACE △．（1）求证：AE BD ⊥；（2）若1,2AD CD ==，试求四边形ABCD 的对角线BD 的长．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】先根据勾股定理求出直角三角形的斜边，即可得出选项．【详解】解：BC ＝BA ＝22125+=，∵数轴上点A 所表示的数为a ，∴a ＝51-故选：C ．【点睛】本题考查了数轴和实数，勾股定理的应用，能读懂图象是解此题的关键．2．D解析：D【分析】设AD ＝DB ＝a ，AF ＝CF ＝b ，BE ＝CE ＝c ，由勾股定理可求a 2+b 2＝c 2，由S 四边形GHCE ＝S 四边形GKJE +S 四边形KHCJ ＝9，可求b ＝2，即可求解．【详解】解：设AD ＝DB ＝a ，AF ＝CF ＝b ，BE ＝CE ＝c ，∴AB2=c，=a，AC2=b，BC2∵∠BAC＝90°，∴AB2+AC2＝BC2，∴2a2+2b2＝2c2，∴a2+b2＝c2，∵将等腰Rt△ADB和等腰Rt△AFC按如图方式叠放到等腰Rt△BEC，∴BG＝GH＝a，∵S四边形GHCE＝S四边形GKJE+S四边形KHCJ＝9，∴1（a+c）（c﹣a）＝9，2∴c2﹣a2＝18，∴b2＝18，∴b＝32，∴AC2=b＝6，故选：D．【点睛】本题考查了勾股定理，折叠的性质，利用整体思想解决问题是本题的关键．3．B解析：B【分析】可依据题意作出简单的图形，结合图形利用勾股定理进行求解，即可．【详解】解：如图所示：∵AC＝20m，BC＝15m，∴在Rt△ABC中，22+m，152025故选：B．【点睛】此题主要考查了勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．4．D解析：D根据勾股定理分别求出正方形E 的面积，进而即可求解．【详解】解：由勾股定理得，正方形E 的面积＝正方形A 的面积＋正方形B 的面积+正方形C 的面积＋正方形D 的面积＝22+32+12+22＝18，∴正方形E 的边长=32．故选：D ．【点睛】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2＋b 2＝c 2．5．D解析：D【分析】由题意∠ACB 为直角，AD=6，利用勾股定理求得BD 的长，进一步求得风车的外围周长．【详解】解：依题意∠ACB 为直角，AD=6，∴CD=6+6=12，由勾股定理得，BD 2=BC 2+CD 2，∴BD 2=122+52=169，所以BD=13，所以“数学风车”的周长是：(13+6)×4=76．故选：D ．【点睛】本题是勾股定理在实际情况中应用，熟练掌握勾股定理是解答本题的关键．在直角三角形中，如果两条直角边分别为a 和b ，斜边为c ，那么a 2+b 2=c 2．6．C解析：C【分析】由勾股定理解得2AB 、22CD BD +，再根据正方形边长相等的性质得到222225CD BD BC AB +===，据此解题即可．解：由勾股定理得，222131225AB =-=222BC CD BD =+222225CD BD BC AB ∴+===∴阴影部分的面积是222252550CD BD BC ++=+=，故选：C ．【点睛】本题考查勾股定理，是重要考点，难度较易，掌握相关知识是解题关键． 7．C解析：C【分析】利用勾股定理求BC 的长度，连接AE ，然后设BE=AE=x ，结合勾股定理列方程求解．【详解】解：如图，∵Rt △ABC 中，∠ACB=90°， ∴22221086BC AB AC =-=-=，∵DE 是AB 的垂直平分线，∴BD=12AB=5，∠EDB=90°，AE=BE 连接AE ，设AE=BE=x ，则CE=x-6在Rt △ACE 中，222(6)8x x -+=，解得：253x =∴BE=AE=253 在Rt △BDE 中，22222520()533BE BD -=-=． 故选：C ．【点睛】本题考查了勾股定理解直角三角形和线段垂直平分线的性质，掌握相关性质定理正确推理计算是解题关键．8．A解析：A【分析】先根据题意画出图形，再根据勾股定理即可得．【详解】由题意，画出图形如下：由勾股定理得：222b a c =+，故选：A ．【点睛】本题考查了勾股定理，依据题意，正确画出图形是解题关键．9．A解析：A【分析】设AC=x 尺，则AB=（10-x ）尺，利用勾股定理解答．【详解】设AC=x 尺，则AB=（10-x ）尺， ABC 中，90ACB ∠=︒，222AC BC AB +=，∴2224(10)x x +=-，解得：x=4.2，故选：A ．【点睛】此题考查勾股定理，根据题意正确设未知数，利用勾股定理解答是解题的关键．10．A解析：A【分析】根据△ADC 为直角三角形且AD=CD ，可得到22211111=2224S AD AC AC =⨯=，同理可得到221=4S BC 及231=4S AB ，在△ACB 中，由勾股定理得出：222AB AC BC =+，继而可得312S S S =+，代入计算即可．【详解】解：∵△ADC 为直角三角形，且AD=CD ，∴在△ADC 中，有222AC AD CD =+，∴222AC AD =，即AC =， ∴22211111=2224S AD AC AC =⨯=， 同理可得：221=4S BC ，231=4S AB ， ∵∠ACB=90︒，∴222AB AC BC =+，即312111444S S S =+， ∴312S S S =+，∵19S =，216S =，∴3129+16=25S S S =+=，故答案为：A ．【点睛】本题考查勾股定理，由勾股定理得出三角形的面积关系是解题的关键．11．C解析：C【分析】设绳索有x 尺长，此时绳索长，向前推出的10尺，和秋千的上端为端点，垂直地面的线可构成直角三角形，根据勾股定理可求解．【详解】解：设绳索有x 尺长，则102+（x+1-5）2=x 2，解得：x=14.5．故绳索长14.5尺．故选：C ．【点睛】本题考查勾股定理的应用，理解题意能力，关键是能构造出直角三角形，用勾股定理来解．12．C解析：C【分析】根据绝对值的非负性及算术平方根的非负性求出m=3，n=4，再分两种情况利用勾股定理求出第三边．【详解】∵30m -=，30m -≥≥，∴m-3=0，n-4=0，解得m=3，n=4，当3、4都是直角三角形的直角边长时，第三边长；当3是直角边长，4是斜边长时，第三边长=故选：C ．【点睛】此题考查绝对值的非负性及算术平方根的非负性，勾股定理，根据绝对值的非负性及算术平方根的非负性求出m=3，n=4是解题的关键．注意：没有明确给出的是直角三角形直角边长还是斜边长时，应分情况求解第三边长．二、填空题13．【分析】根据题意得到圆心O 的位置设MO=x 根据AO2=DO2得到方程求出x 得到圆O 的半径从而求出面积【详解】解：由题意可得：多个小正方形排成轴对称图形∴圆心O 落在对称轴MN 上设MO=x ∵AO=DO ∴ 解析：1309π 【分析】根据题意得到圆心O 的位置，设MO=x ，根据AO 2=DO 2，得到方程，求出x ，得到圆O 的半径，从而求出面积．【详解】解：由题意可得：多个小正方形排成轴对称图形，∴圆心O 落在对称轴MN 上，设MO=x ，∵AO=DO ，∴AO 2=DO 2，即()2222163x x +=-+，解得：x=113，∴圆O的半径为21x+=1303，∴圆O的面积为21303π⎛⎫⎪⎪⎝⎭=1309π，故答案为：1309π．【点睛】本题考查了勾股定理，轴对称的性质，圆的性质，解题的关键是根据半径相等得到方程．14．【解析】如图(1)所示：AB=；如图(2)所示：AB=∵>∴最短路径为答：它所行的最短路线的长是故答案为点睛：本题考查了平面展开---最短路径问题解题的关键是将长方体展开构造直角三角形然后利用勾股定解析：41【解析】如图(1)所示：222(25)=53++如图(2)所示：2245=41+，∵5341∴414141点睛：本题考查了平面展开---最短路径问题，解题的关键是将长方体展开，构造直角三角形，然后利用勾股定理解答.15．10或6【解析】试题解析：10或6【解析】试题根据题意画出图形，如图所示，如图1所示，AB =10，AC 10，AD =6，在Rt △ABD 和Rt △ACD 中，根据勾股定理得：BD 22AB AD -，22AC AD -=2，此时BC =BD +CD =8+2=10；如图2所示，AB =10，AC 10，AD =6，在Rt △ABD 和Rt △ACD 中，根据勾股定理得：BD 22AB AD -，CD 22AC AD -=2，此时BC =BD -CD =8-2=6，则BC 的长为6或10． 16．4【分析】应用勾股定理和正方形的面积公式可求解【详解】∵勾弦∴股b=∴小正方形的边长＝∴小正方形的面积故答案为4【点睛】本题运用了勾股定理和正方形的面积公式关键是运用了数形结合的数学思想解析：4【分析】应用勾股定理和正方形的面积公式可求解．【详解】∵勾a 6=，弦c 10=，∴股221068-=，∴小正方形的边长＝862-=，∴小正方形的面积224==故答案为4【点睛】本题运用了勾股定理和正方形的面积公式，关键是运用了数形结合的数学思想． 17．﹣1或5【分析】根据点M （24）与点N （x4）之间的距离是3可以得到|2-x|=3从而可以求得x 的值【详解】解：∵点M （24）与点N （x4）之间的距离是3∴|2﹣x|＝3解得x＝﹣1或x＝5故答案为解析：﹣1或5【分析】根据点M（2，4）与点N（x，4）之间的距离是3，可以得到|2-x|=3，从而可以求得x的值．【详解】解：∵点M（2，4）与点N（x，4）之间的距离是3，∴|2﹣x|＝3，解得，x＝﹣1或x＝5，故答案为﹣1或5．【点睛】本题考查两点间的距离，解题的关键是明确题意，找出所求问题需要的条件．18．6【分析】根据题意和图形可以得到AB2和AC2再根据△ABC是直角三角形和勾股定理可以得到BC2【详解】解：∵两个正方形的面积分别是S1=18S2=12∴AB2=18AC2=12∵△ABC是直角三角解析：6【分析】根据题意和图形，可以得到AB2和AC2，再根据△ABC是直角三角形和勾股定理，可以得到BC2．【详解】解：∵两个正方形的面积分别是S1=18，S2=12，∴AB2=18，AC2=12，∵△ABC是直角三角形，∴BC2=AB2-AC2=18-12=6，故答案为：6．【点睛】本题考查了正方形的性质，解题的关键是明确题意，利用数形结合的思想解答．19．【分析】有三种展开方式一种是正面和右侧面展开如图（1）一种是正面和上面展开如图（2）另外一种是底面和右侧面展开如图（3）分别根据勾股定理求AB的长度即可判断【详解】正面和右侧面展开如图（1）根据勾股解析：【分析】有三种展开方式，一种是正面和右侧面展开如图（1），一种是正面和上面展开如图（2），另外一种是底面和右侧面展开如图（3），分别根据勾股定理求AB的长度即可判断．【详解】正面和右侧面展开如图（1）根据勾股定理()2223126AB =++=；正面和上面展开如图（2）根据勾股定理()2213225AB =++=；底面和右侧面展开如图（3）根据勾股定理()2212332AB =++= ∵322526<<∴最短的路径是32故答案为32【点睛】本题考察了几何图形的展开图形，勾股定理的实际应用，容易漏掉正面和上面的展开图是本题的易错点，在做题的过程中要注意考虑全面．20．9cm 【分析】由可知为直角三角形利用勾股定理可分别计算求得BC 和CD 从而完成BD 求解【详解】∵∴同理∴故答案为：【点睛】本题考察了勾股定理的知识点；求解的关键是熟练掌握并运用勾股定理求解直角三角形边长 解析：9cm【分析】由90C ∠=︒可知ABC 为直角三角形，利用勾股定理，可分别计算求得BC 和CD ，从而完成BD 求解．∵90C ∠=︒∴15BC ==同理6CD ===∴1569BD BC CD =-=-=故答案为：9cm ．【点睛】本题考察了勾股定理的知识点；求解的关键是熟练掌握并运用勾股定理求解直角三角形边长．三、解答题21．2秒【分析】设P 、Q 两点运动x 秒时，P 、Q 两点间的距离是厘米，先利用勾股定理求出AC 的长度，得到AP=2x 厘米，CQ=x 厘米，CP=（10﹣2x ）厘米，再利用勾股定理得到（10﹣2x ）2+x 2=（）2求出x 的值.【详解】解：设P 、Q 两点运动x 秒时，P 、Q 两点间的距离是厘米.在△ABC 中，∠C=90°，BC=5厘米，∴=（厘米），∴AP=2x 厘米，CQ=x 厘米，CP=（10﹣2x ）厘米，在Rt △CPQ 内有PC 2+CQ 2=PQ 2，∴（10﹣2x ）2+x 2=（）2，整理得：x 2﹣8x+12=0，解得：x=2或x=6，当x=6时，CP=10﹣2x=﹣2＜0，∴x=6不合题意舍去.∴P 、Q 两点运动2秒时，P 、Q 两点间的距离是厘米.【点睛】此题考查勾股定理，动点问题与几何图形，熟练掌握勾股定理的计算公式并运用解决问题是关键.22．36【分析】连接AC ，在直角三角形ABC 中，根据勾股定理计算得到AC 的长度，继而由勾股定理的逆定理求出∠ACD 为90°，计算得到四边形的面积即可．【详解】在Rt△ABC中，有AC2=AB2+BC2=4²+3²=25，又AC>0，∴AC=5∵AC2+CD²=52+12²=169=13²=AD²∴∠ACD=90°，S四边形ABCD= 12AB×BC+12AC×CD=36.【点睛】本题考查了勾股定理，勾股定理的逆定理的应用，解此题的关键是能求出△ABC和△CAD 的面积，注意：如果一个三角形的两边的平方和等于第三边的平方，那么这个三角形是直角三角形．23．5米【分析】利用勾股定理计算即可.【详解】由题意知：10米，AC=5.5米，∵∠ABC=90°，∴2222(5.5)(10)BC AC AB=-=-米，答：棍子和地面接触点C到小树底部B的距离是4.5米.【点睛】此题考查勾股定理的实际应用，根据实际问题构建直角三角形利用勾股定理来解决问题是解题的关键.24．（1）2.5；（2）2或2.5或1.5【分析】（1）根据格点C在线段AB右侧，且满足AC=BC，画出周长最小的格点△ABC，即可求出△ABC的面积；（2）根据格点D在线段AB左侧，且满足AD⊥BD，分别画出格点△ABD，即可得三角形的面积．【详解】解：（1）如图，△ABC 即为所求；△ABC 的面积为：1552⨯⨯=2.5， 故答案为：2.5；（2）如图点D 1，D 2，D 3 即为所求；△ABD 的面积分别为：12222⨯⨯=2， 1552⨯⨯=2.5， 1132⨯⨯=1.5， 故答案为：2或2.5或1.5．【点睛】此题主要考查了格点图形的性质，把握格点图形的定义，正确画出格点三角形是解决问题的关键．25．76【分析】根据题意可知∠ACB 为直角，利用勾股定理求得外围中一条边，又由AC 延伸一倍，从而求得风车的一个轮子，进一步求得四个即风车的外围周长．【详解】解：解：依题意，设“数学风车”中的四个直角三角形的斜边长为x ，则222125169x =+=所以x=13所以“数学风车”的外围周长是：（13+6）×4=76．【点睛】本题考查勾股定理在实际情况中的应用，注意掌握运用隐含的已知条件来解答此类题. 26．（1）见解析；（2）3BD =．【分析】()1证明：由BCD 绕点C 顺时针旋转到ACE △，利用旋转性质得BC=AC ，12∠=∠，由∠ABC =45º，可知∠ACB=90º，由1390∠+∠=︒，可证2490∠+∠=︒ 即可，()2解:连DE ，由BCD ∆绕点C 顺时针旋转到ACE ∆，得BCD ACE ∠=∠，CD=CE=2，BD=AE ，利用等式性质得90DCE ACB ∠=∠=︒，∠CDE=45º，利用勾股定理DE=22，由∠ADC=45º可得∠ADE=90º，由勾股定理可求AE 即可．【详解】()1证明：BCD 绕点C 顺时针旋转一定角度后，点B 的对应点恰好与点A 重合，得到ACE △， ,12BC AC ∴=∠=∠，45,ABC BAC ∴∠=∠=︒18090,ACB ABC BAC ∴∠=︒∠∠=︒－－1390,∴∠+∠=︒又34,∠=∠241390,∴∠+∠=∠+∠=︒1802490,ANM ∴∠=︒-∠-∠=︒即AE BD ⊥，()2解:连DE ，BCD 绕点C 顺时针旋转一定角度后，点B 的对应点恰好与点A 重合，得到,ACEBCD ACE ∴∠=∠，即,2,ACB ACD DCE ACD CD CE BD AE ∠+∠=∠+∠===，90,DCE ACB ∴∠=∠=︒2222228,DE CD CE ∴=+=+=又90,2,DCE CD CE ∠=︒==45,CDE ∴∠=︒90,ADE ADC CDE ∴∠=∠+∠=︒∴===，3AE∴=．BD3【点睛】本题考查旋转的性质和勾股定理问题，关键是掌握三角形旋转的性质与勾股定理知识，会利用三角形旋转性质结合∠ABC=45º证∠ACB=90º，利用余角证AE⊥BD，利用等式性质证∠DCE=90º，利用勾股定理求DE，结合∠ADC=45º证Rt△ADE,会用勾股定理求AE使问题得以解决．。

初二勾股定理练习题电子版1. 已知直角三角形的两条直角边长分别为3cm和4cm，请问斜边长多少？解答：根据勾股定理，斜边的平方等于两直角边的平方和。

设斜边长为c，根据公式可得：c² = 3² + 4²c² = 9 + 16c² = 25所以，斜边长c为5cm。

2. 在直角三角形ABC中，已知斜边长为10cm，一条直角边长为6cm，请问另一条直角边长多少？解答：同样根据勾股定理，设另一条直角边长为a，可得：a² + 6² = 10²a² + 36 = 100a² = 100 - 36a² = 64所以，另一条直角边长a为8cm。

3. 已知直角三角形的两条直角边分别为5cm和12cm，请问斜边长多少？解答：根据勾股定理，设斜边长为c，可得：c² = 5² + 12²c² = 25 + 144c² = 169所以，斜边长c为13cm。

4. 在直角三角形XYZ中，已知斜边长为15cm，一条直角边长为9cm，请问另一条直角边长多少？解答：根据勾股定理，设另一条直角边长为b，可得：b² + 9² = 15²b² + 81 = 225b² = 225 - 81b² = 144所以，另一条直角边长b为12cm。

5. 若直角三角形的两条直角边分别为xcm和ycm，斜边长为zcm，根据勾股定理，我们可以得到一个关系式，即x² + y² = z²。

请用这个关系式回答以下问题：(1) 如果x=5cm，y=12cm，求z的值。

解答：根据关系式x² + y² = z²，代入x、y的值可得：5² + 12² = z²25 + 144 = z²169 = z²所以，z的值为13cm。

八年级数学(上)第二章勾股定理与平方根第3课时神秘的数组（附答案）1．以下列各组数作为三角形三边的长，不能构成直角三角形的是( ) A．5，12，13 B．7，24，25 C．8，15，17 D．4，6，92．在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，下列说法中正确的个数有( )①如果∠B－∠C=∠A，则△ABC是直角三角形；②如果c2=b2－a2，则△ABC是直角三角形，且∠C=90°；③如果(c+a)(c一a)= b2，则△ABC是直角三角形；④如果∠A：∠B：∠C =5：2：3，则△ABC是直角三角形．A．1 B．2 C．3 D．43．满足下列条件的三角形中，不是直角三角形的是( ) A．三内角之比为l：2：3 B．三边平方的比为1：2：3C．三边长为41，40，9 D．三边长为10，15，20，4．若3条线段的长a、b、c满足a2－c2=b2，那么这3条线段组成的三角形是_____三角形．5．已知三角形三边长分别为a、b、c，满足等式(a+b)2－c2=2ab．则此三角形是______三角形．6．一个三角形的三边长之比为3：4：5，则这个三角形是__________．7．三角形的最长边为5，最短边为3，要使它成为直角三角形，则第三边边长为________．8．若三角形的三边长分别为a+1，a+2，a+3，则当a=_______时，此三角形为直角三角形．9．以三角形的三边为边长的三个正方形的面积分别为9、16、25，则这个三角形的面积为_______．10．如图所示，每个小方格都是边长为l的正方形，点A、B是方格纸的两个格点(即正方形的顶点)，在这个6×6的方格纸中，找出格点C，使△ABC的面积为1个平方单位的直角三角形的点的个数是___________．11．下列各组数是勾股数吗?为什么?(1)8，15，17；(2)7，12，15；(3)12，15，20；(4)15，20，25．12．如图，在△ABC中，AB=13，AD=5，BC=24，A D⊥BC于点D．试说明△ABC是等腰三角形．13．如果一个三角形的三边a、b、c满足下列条件，判断它是否是直角三角形，并说明理由．(1)a=9，b=40，c=41．(2)a=2x，b=2x，c=3x(其中x>0)．(3)a=n+1，b=n－1，c=n．(4)a=n2－1，b=2n，c=n2+1(n为大于l的整数)．14．如下表所示，表中所给的每行三个数a、b、c满足a<b<c，则根据表中已有数据的规律，可得当a=20时，b=__________，c=___________．15．如图，在四边形花圃ABCD中，AB=9 m，BC=12 m，CD=20 cm，AD=25 m，∠B=90°．求这个四边形花圃ABCD的面积．16．如图，AD=4，CD=3，∠ADC=90°，AB=13，BC=12．求四边形ABCD的面积．17．如图(1)所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图(2)所示，已知展开图中每个正方形的边长为1．试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系．参考答案1．D 2．C 3．D4．直角 5．直角 6．直角三角形 7．4 8．2 9．6 10．6 11．(1)、(4)是勾股数12．在R t △ABD 中，∵BD 2=AB 2－AD 2=144，∴BD=12．∵BC=24．∴D 为BC 的中点．又∵AD ⊥BC ，∴AB=AC ．∴△ABC 为等腰三角形13．(1)是 (2)不是 (3)当n=4时是，当n ≠4时不是 (4)是 14．99 10115．连接AC ．在Rt △ABC 中．∵AC 2=AB 2+BC 2=225，AD 2=625，CD 2=400．∴AD 2=AC 2+CD 2．∴△ADC 是直角三角形，∠ACD=90°．∴S四边形ABCD=12×9×12+12×15×20=204(m 2) 16．连接AC ．∵CD ⊥AD ，AD=4，CD=30．∴AC=5．∵AB=13，BC=12，又∵52+122=132．∴AC 2+BC 2=AB 2．∴△ABC 为直角三角形．∴四边形ABCD 的面积为S四边形ABCD=12AC BC －12AD CD=24 17．∠BAC=∠B ′A ′C ′。

八年级数学(上)第二章勾股定理与平方根第4课时平方根(一)（附答案）1．(1)因为32=9，(－3) 2=_________，所以3和－3都是_________的平方根；(2)2有_________个平方根，它们互为________数，记作________；(3)4的平方根是__________；(4)__________的平方根．2．若a、b分别是10的平方根，则a+b=________．3．(1)一个数的平方等于它本身，这个数是__________；(2)一个数的平方根等于它本身，这个数是_________．4．(1)16的平方根是________；0．25的平方根是________；1649的平方根是_________；(2)2．56的平方根是_________；(－2) 2的平方根是_________；10－2的平方根是_______．5．若4x+1的平方根是±5，则x=________．若x 2=16，则5－x的平方根是_________．6．一个正数n的两个平方根为m+1和m－3，则m=_________，n=__________．7．若式子13x-的平方根只有一个，则x的值是__________．8．下列说法正确的是( )A．116的平方根是14B．任何有理数都有平方根C．任何非负数都有两个平方根D．一个正数的两个平方根的和等于零9．下列各数中没有平方根的是( )A．216⎛⎫- ⎪⎝⎭B．216⎛⎫- ⎪⎝⎭C．216⎛⎫± ⎪⎝⎭D．1610．求下列各数的平方根：(1)144；(2)21；(3)116；(4)10－4；(5)(－3) 2．11．求下列各式中的x：(1)x2=36；(2)9－x2=0．12．下列各数有平方根吗?如果有，求出它的平方根；如果没有，说明理由．(1)－64；(2)0；(3)(－4) 2；(4)10－2．13．求下列方程中的x：(1)x 2+9 2=41 2；(2)x 2=(－4) 2；(3)(1－x) 2=9 2；(4)(2x－3) 2－9=16．14．(1)一个正数的平方等于361，求这个正数．(2)一个负数的平方等于169，求这个负数．(3)一个数的平方等于121，求这个数．参考答案1．(1)9 9 (2)2 相反(3)±2 (4)5 2．0 3．(1)1，0 (2)04．(1)±4 ±0．547±(2)±1．6 ±2110±5．6 ±3或±1 6．1 4 7．1 38．D 9．B10．(1)±12 (2)(3)14±(4)±10－2(5)±311．(1)x=±6 (2)x=±312．(1)没有理由略(2)0 (3)±4 (4)±10－113．(1)x=±40 (2)x=±4 (3)x=－8或x =10 (4)x=4或x=－1 14．(1)19 (2)－13 (3)±11。

第二章勾股定理与平方根检测卷（附答案）（总分100分时间90分钟）一、选择题（每小题3分，共30分）1．下列各组数中，不能作为直角三角形三边长的是( )A．9，12，15 B．7，24，25 C．6，8，10 D．3，5，7 2．(－6)2的平方根是( )A．－6 B．36 C．±6 D3．下列说法中不正确的是( )A．－2是4的一个平方根B8的立方根C．立方根等于它本身的数只有1和0 D．平方根等于它本身的数只有0 4．下列说法正确的是( )A．无限小数是无理数B．带根号的数都是无理数C．无理数是无限小数D．无理数是开方开不尽的数5．下列说法中正确的有( )①0的平方根是0；②1的平方根是1；③－1是1的平方根；④－1是－1的平方根；⑤8A．1个B．2个C．3个D．4个6．如图一直角三角形纸片，两直角边AC＝6 cm，BC＝8 cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于( )A．2 cm B．3 cmC．4 cm D．5 cm7．把32. 982保留三个有效数字，并用科学记数法表示为( )A．3.92×10 B．3.2982×10 C．33.0 D．3.30×108．数轴上的任何一点表示( )A．有理数B．无理数C．实数D．正数和负数9．如果梯子的底端离建筑物5米，13米长的梯子可以达到该建筑物的高度是( ) A．12米B．13米C．14米D．15米10．要从电杆离地面4m处向地面拉—条长为5m的电缆，则地面电缆固定点与电线杆底部的距离应为( )A．5 m B．4 m C．3 m D．2 m二、填空题（每小题2分，共16分）11．直角三角形两条直角边的长分别为5、12，则斜边上的高为______．y+=，12_______()260则x＋y＝______．13．如图，在锐角三角形ABC中，AD⊥BC，AD＝12，AC＝13，BC＝14．则AB＝______．14．如图是一个育苗棚，棚宽a＝6 m，棚高b＝2.5 m，棚长d＝10 m，则覆盖在棚斜面上的塑料薄膜的面积为______m2．15．如图所示，15只空油桶(每只油桶底面直径均为60 cm)堆在一起，要给它盖一个遮雨棚，遮雨棚起码要_______cm 高．16．若一正数的两个平方根是2a －l 与－a ＋2，则a ＝______．17．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A 、B 、C 、D 的边长分别是3、5、2、3，则最大正方形E 的面积是______．18．如图，已知Rt △ABC 是直角边长为1的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，…，依此类推，第n 个等腰直角三角形的斜边长是______． 三、解答题(19题8分，20题6分，其余每题各10分，共54分) 19．求下列各式中x 的值(1)5x 2－10＝0； (2)25(m ＋2)2－49＝0；20．把下列实数填在相应的集合中2273，0.1，－0.010010001…，－5． 正整数集合{ }． 正有理数集合{ }． 无理数集合{ }．21．《中华人民共和国道路交通管理条例》规定：小汽车在城市街道上的行驶速度不得超过70千米／时．一辆“小汽车”在一条城市街道上直道行驶，如图某一时刻刚好行驶到路对面“车速检测仪A ”正前方50米C 处，过了6秒后，测得“小汽车”位置B 与“车速检测仪A ”之间的距离为130米，这辆“小汽车”超速了吗？请说明理由．22．如图，一张长方形纸片宽AB ＝8 cm ，长BC ＝10 cm ．现将纸片折叠，使顶点D 落在BC 边上的点F 处(折痕为AE)，求EC 的长．23．先观察下列等式，再回答问题：111111112=+-=+111112216=+-=+1111133112=+-=+…(1) (2)请按照上面各等式反映的规律，试写出用n(n 为正整数)表示的等式．24．在图中．正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE＝2b，且边AD和AE在同一直线上．操作示例当2b<a时，如图①，在BA上选取点G，使BG＝b，连接FG和CG，裁掉△FAG 和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH．思考发现小明在操作后发现：该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH 的位置，易知EH与AD在同一直线上，连接CH，由剪拼方法可得DH＝BG，故△CHD≌△CGB，从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置．这样，对于剪拼得到的四边形FGCH（如图①），过点F作FM⊥AE于点M(图略)，利用“SAS”可判断△HFM≌△CHD，易得FH＝HC＝GC＝FG，∠FHC＝90°．进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．实践探究(1)正方形FGCH的面积是______ ；（用含a，b的式子表示）(2)类比①的剪拼方法，请你就②～④的三种情形分别画出剪拼成一个新正方形的示意图．联想拓展小明通过探究后发现：当b≤a时，此类图形都能剪拼成正方形，且所选取的点G 的位置在BA方向上随着b的增大不断上移．当b>a时，如⑤的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．参考答案1．D 2．C 3．C 4．C 5．B 6．B 7．D 8．C 9．A 10．C 11．601312．±2，±1，0 －213．15 14．65 15．60) 16．－1 17．47 1819．(1)x (2)m ＝－35或－17520．正整数集合{．正有理数集合{227，0.1}．无理数集合3π，－0.010010001…}． 21．小汽车超速了． 22．EC 长3cm23．(1)1111144120+-=- (2) 11(1)n n =++ 24．(1)22a b +(2)剪拼方法如图联想拓展 能； 剪拼方法如图④。

《勾股定理和平方根》单元测试9.22命题：徐红石 审核：席美丽 时间：45分钟班级 姓名____ ___学号一、选择题（本题共5题，每题3分，共15分）1．下列几组数中不能作为直角三角形三边的是 （ ）A a 7,b 24,c 25===B 1.5,2, 2.5a b c ===C 25,2,34a b c ===D 15,8,17a b c === 2．小强量得家里彩电屏幕长为cm 58，宽为cm 46，则这台彩电尺寸（即为对角线）是（ ）A 9英寸（23cm ）B 21英寸（54cm ）C 29英寸（74cm ）D 34英寸（87cm ）3．等腰三角形腰长5cm ，底边6cm ，其面积是 （ ）A 248cmB 224cmC 212cmD 216cm4．直角三角形边长为b a ,，斜边上高为h ，则下列各式总能成立的是（ ）A 2ab h =B 2222a b h +=C 111a b h+= D 222111a b h += 5．如图一直角三角形纸片，两直角边6,8AC cm BC cm ==，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（ ）A cm 2B cm 3C cm 4D cm 5 二、填空题（本题共15空，每空3分，共45分）6．下列实数(1)3.1415926 .(2)0.3 22(3)7(5)- (6)2(7)0.3030030003... 其中无理数有 ，有理数有 ．（填序号）7．49的平方根________，0.216的立方根________．________， 8．算术平方根等于它本身的数有 ，立方根等于本身的数有________．9．若2256x =，则x =______ __，若3216x =-，则x =________．10．已知甲往东走了4km ，乙从同处出发往南走了3km ，这时甲、乙俩人相距 .A EB DC 第5题图11，则它的算术平方根是 .12．x是2(-的平方根，y 是64的立方根，则x y += .13．如果2(6)0y +=，则x y += ．14．如果21a -和5a -是一个数m 的平方根，则.a =15．直角三角形三角形两直角边长为3和4，三角形内一点到各边距离相等，那么这个距离为 ．三、计算题（本题共2题，每题4分，共8分）16．求下列各式中x 的值2(1)(1)25x -=；； 3(2)(3)27x --=．四、作图题（本题共2题，每题4分，共8分）17．在数轴上画出-18．下图的正方形网格，每个正方形顶点叫格点，请在图中画一个面积为10的正方形．第17题图第18题图— 3 —五、解答题（本题共4题，每题6分，共24分）19．如图，一根电线杆因超过使用寿命被大风刮倒，折断处离地面9m ，电线杆顶部在离电线杆底部12m ，处，这根电线杆在折断前有多少米？20．已知如图所示，四边形ABCD 中，3,4,13,12AB cm AD cm BC cm CD cm==== 090A ?求四边形ABCD 的面积．21．如图，有一只小鸟上从小树顶飞到大树顶上，请问它飞行的最短路程是多少米？（先画出示意图，然后再求解）．A 第19题图22拼图填空：材料：硬纸板、剪刀、三角板，方法：剪裁、拼图、探索，操作：剪裁出若干个大小、形状完全相同的直角三角形，三边长分别记为a、b、c，如图①。

八年级上册数学评价检测试卷第一章勾股定理一、选择题1．以下列各组数据为三角形三边，能构成直角三角形的是（ ） （A ）4cm ，8cm ，7cm （B ） 2cm ，2cm ，2cm （C ） 2cm ，2cm ，4cm （D ）13cm ，12 cm ，5 cm2．一个三角形的三边长分别为15cm ，20cm ，25cm ，则这个三角形最长边上的高为（ ） （A ）12cm （B ）10cm （C ）12.5cm （D ）10.5cm3．Rt ∆ABC 的两边长分别为3和4，若一个正方形的边长是∆ABC 的第三边，则这个正方形的面积是（ ） （A ）25 （B ）7 （C ）12 （D ）25或74．有长度为9cm ，12cm ，15cm ，36cm ，39cm 的五根木棒，可搭成（首尾连接）直角三角形的个数为 （ ） （A ）1个 （B ）2个 （C ）3个 （D ）4个5．将直角三角形的三边长扩大相同的倍数后，得到的三角形是（ ） （A ）直角三角形 （B ）锐角三角形 （C ）钝角三角形 （D ）以上结论都不对 6．在△ABC 中，AB =12cm ， AC =9cm ，BC =15cm ，下列关系成立的是（ ） （A ）B C A ∠+∠>∠ （B ）B C A ∠+∠=∠ （C ）B C A ∠+∠<∠ （D ）以上都不对7．小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m 远的水底，竹竿高出水面0.5m ，把竹竿的顶端拉向岸边，竿顶和岸边的水平刚好相齐，河水的深度为（ ）（A ）2m （B ）2.5cm （C ）2.25m （D ）3m 8．若一个三角形三边满足ab c b a 2)(22=-+，则这个三角形是（ ）（A ）直角三角形 （B ）等腰直角三角形 （C ）等腰三角形 （D ）以上结论都不对 9．一架250cm 的梯子斜靠在墙上，这时梯足与墙的终端距离为70cm ，如果梯子顶端沿墙下滑40cm ，那么梯足将向外滑动（ ） （A ）150cm（B ）90cm（C ）80cm（D ）40cm10．三角形三边长分别为12+n 、n n 222+、1222++n n （n 为自然数），则此三角形是（ ） （A ）直角三角形 （B ）等腰直角三角形 （C ）等腰三角形 （D ）以上结论都不对二、填空题11．写四组勾股数组.______，______，______，______.12．若一个直角三角形的三边为三个连续的偶数，则它的周长为____________。

第一章勾股定理一、选择题（每题4分，共28分）1．（2018•滨州）在直角三角形中，若勾为3，股为4，则弦为（）A．5 B．6 C．7 D．82．（4分）（2017•兴安盟）下列长度的三条线段能组成锐角三角形的是（）A．6，8，14 B．6，8，12 C．6，8，10 D．6，8，83．（4分）如图，正方形ABCD的边长为1，则正方形ACEF的面积为（）A．2 B．3 C．4 D．54．（4分）如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（）A．12米B．13米C．14米D．15米5．（4分）满足下列条件的△ABC中，不是直角三角形的是（）A．a:b:c=3:4:5 B．∠A:∠B:∠C=1:2:3C．a2:b2:c2=1:2:3 D．a2:b2:c2=3:4:56．（4分）若等腰三角形中相等的两边长为10cm，第三边长为16cm，那么第三边上的高为（）A．12 cm B．10 cm C．8 cm D．6 cm7．（4分）如图，正方形网格中的△ABC，若小方格边长为1，则△ABC的形状为（）A．直角三角形B．锐角三角形C．钝角三角形D．以上答案都不对二、填空:（每空4分，共计28分）8．（4分）已知一个Rt△的两边长分别为3和4，则第三边长的平方为．9．（4分）求如图中直角三角形中未知的长度:b= ，c= ．10．（4分）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积之和为cm2．11．（4分）小明把一根70cm长的木棒放到一个长、宽、高分别为40cm、30cm、50cm的木箱中，他能放进去吗？答: （填“能”、或“不能”）12．（4分）（2018•襄阳）已知CD是△ABC的边AB上的高，若CD＝，AD＝1，AB＝2AC，则BC的长为．13．（4分）（2018•福建）把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB＝，则CD＝．14．（4分）（2018•黄冈）如图，圆柱形玻璃杯高为14cm，底面周长为32cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为cm（杯壁厚度不计）．三、解答题:（每题11分，共计44分）15．（11分）一棵树在离地面9米处断裂，树的顶部落在离树根底部12米处，求树折断之前的高度？（自己画图并解答）16．（11分）小东与哥哥同时从家中出发，小东以6km/时的速度向正北方向的学校走去，哥哥则以8km/时的速度向正东方向走去，半小时后，小东距哥哥多远？17．（11分）如图所示，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，∠A=90°; （1）求BD的长;（2）求四边形ABCD的面积．18．（11分）如图，有一个直角三角形纸片，两直角边AB=6cm，BC=8cm，现将直角边BC沿直线BD折叠，使点C落在点E处，求三角形BDF的面积是多少？四、附加题19．如图所示的一块地，AD=12m，CD=9m，∠ADC=90°，AB=39m，BC=36m，求这块地的面积．20．如图，△ABC是直角三角形，∠BAC=90°，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF．（1）如图1，试说明BE2+CF2=EF2;（2）如图2，若AB=AC，BE=12，CF=5，求△DEF的面积．参考答案一、选择题（每题4分，共28分）1．（2018•滨州）在直角三角形中，若勾为3，股为4，则弦为（）A．5 B．6 C．7 D．8【分析】直接根据勾股定理求解即可．【解答】解:∵在直角三角形中，勾为3，股为4，∴弦为＝5．故选:A．【点评】本题考查了勾股定理:在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．2．（4分）（2017•兴安盟）下列长度的三条线段能组成锐角三角形的是（）A．6，8，14 B．6，8，12 C．6，8，10 D．6，8，8【考点】KS:勾股定理的逆定理．【专题】55:几何图形．【分析】根据勾股定理求出以较短的两条边为直角边的三角形的斜边的长度，然后与较长的边进行比较作出判断即可．【解答】解:A、∵6+8＝14，∴不能组成三角形;B、＝10＜12，6+8＞12，∴不能组成锐角三角形;C、∵＝10是直角三角形，∴不能组成锐角三角形;D、∵＝10＞8，6+8＞8，∴能组成锐角三角形．故选:D．【点评】本题考查了勾股定理的逆定理，利用勾股定理求出直角三角形的斜边是解题的关键．3．（4分）如图，正方形ABCD的边长为1，则正方形ACEF的面积为（）A．2 B．3 C．4 D．5【考点】算术平方根．【分析】根据勾股定理，可得AC的长，再根据乘方运算，可得答案．【解答】解:由勾股定理，得AC=，乘方，得（）2=2，故选:A．【点评】本题考查了算术平方根，先求出AC的长，再求出正方形的面积．4．（4分）如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（）A．12米B．13米C．14米D．15米【考点】勾股定理的应用．【专题】应用题．【分析】根据梯子、地面、墙正好构成直角三角形，再根据勾股定理解答即可．【解答】解:如图所示，AB=13米，BC=5米，根据勾股定理AC===12米．故选A．【点评】此题是勾股定理在实际生活中的运用，比较简单．5．（4分）满足下列条件的△ABC中，不是直角三角形的是（）A．a:b:c=3:4:5 B．∠A:∠B:∠C=1:2:3C．a2:b2:c2=1:2:3 D．a2:b2:c2=3:4:5【考点】勾股定理的逆定理;三角形内角和定理．【分析】由勾股定理的逆定理得出A、C是直角三角形，D不是直角三角形;由三角形内角和定理得出B是直角三角形;即可得出结果．【解答】解:∵a:b:c=3:4:5，32+42=52，∴这个三角形是直角三角形，A是直角三角形;∵∠A:∠B:∠C=1:2:3，∴∠C=90°，B是直角三角形;∵a2:b2:c2=1:2:3，∴a2+b2=c2，∴三角形是直角三角形，C是直角三角形;∵a2:b2:c2=3:4:5，∴a2+b2≠c2，∴三角形不是直角三角形;故选:D【点评】本题考查了勾股定理的逆定理、三角形内角和定理;熟练掌握勾股定理的逆定理和三角形内角和定理，通过计算得出结果是解决问题的关键．6．（4分）若等腰三角形中相等的两边长为10cm，第三边长为16cm，那么第三边上的高为（）A．12 cm B．10 cm C．8 cm D．6 cm【考点】勾股定理;等腰三角形的性质．【分析】根据等腰三角形的性质先求出BD，然后在RT△ABD中，可根据勾股定理进行求解．【解答】解:如图:由题意得:AB=AC=10cm，BC=16cm，作AD⊥BC于点D，则有DB=BC=8cm，在Rt△ABD中，AD==6cm．故选D．【点评】本题考查了等腰三角形的性质及勾股定理的知识，关键是掌握等腰三角形底边上的高平分底边，及利用勾股定理直角三角形的边长．7．（4分）如图，正方形网格中的△ABC，若小方格边长为1，则△ABC的形状为（）A．直角三角形B．锐角三角形C．钝角三角形D．以上答案都不对【考点】勾股定理的逆定理;勾股定理．【专题】网格型．【分析】根据勾股定理求得△ABC各边的长，再利用勾股定理的逆定理进行判定，从而不难得到其形状．【解答】解:∵正方形小方格边长为1，∴BC==2，AC==，AB==，在△ABC中，∵BC2+AC2=52+13=65，AB2=65，∴BC2+AC2=AB2，∴△ABC是直角三角形．故选:A．【点评】考查了勾股定理的逆定理，解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．二、填空:（每空4分，共计28分）8．（4分）已知一个Rt△的两边长分别为3和4，则第三边长的平方为7或25 ．【考点】勾股定理．【分析】已知的这两条边可以为直角边，也可以是一条直角边一条斜边，从而分两种情况进行讨论解答．【解答】解:分两种情况:当3、4都为直角边时，第三边长的平方=32+42=25;当3为直角边，4为斜边时，第三边长的平方=42﹣32=7．故答案为:7或25．【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．9．（4分）求如图中直角三角形中未知的长度:b= 12 ，c= 10 ．【考点】勾股定理．【分析】根据勾股定理进行计算即可．【解答】解:b==12;c==10，故答案为:12;10．【点评】本题考查的是勾股定理的应用，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．10．（4分）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积之和为49 cm2．【考点】勾股定理．【分析】根据正方形的面积公式，连续运用勾股定理，发现:四个小正方形的面积和等于最大正方形的面积．【解答】解:由图形可知四个小正方形的面积和等于最大正方形的面积，故正方形A，B，C，D的面积之和=49cm2．故答案为:49cm2．【点评】熟练运用勾股定理进行面积的转换．11．（4分）小明把一根70cm长的木棒放到一个长、宽、高分别为40cm、30cm、50cm的木箱中，他能放进去吗？答: 能（填“能”、或“不能”）【考点】勾股定理的应用．【分析】能，在长方体的盒子中，一角的顶点与斜对的不共面的顶点的距离最大，根据木箱的长，宽，高可求出最大距离，然后和木棒的长度进行比较即可．【解答】解:能，理由如下:可设放入长方体盒子中的最大长度是xcm，根据题意，得x2=502+402+302=5000，702=4900，因为4900＜5000，所以能放进去．故答案为能．【点评】本题考查了勾股定理的应用，解题的关键是求出木箱内木棒的最大长度．12．（4分）（2018•襄阳）已知CD是△ABC的边AB上的高，若CD＝，AD＝1，AB＝2AC，则BC的长为2或2．【考点】KQ:勾股定理．【专题】552:三角形．【分析】分两种情况:①当△ABC是锐角三角形，如图1，②当△ABC是钝角三角形，如图2，分别根据勾股定理计算AC和BC即可．【解答】解:分两种情况:①当△ABC是锐角三角形，如图1，∵CD⊥AB，∴∠CDA＝90°，∵CD＝，AD＝1，∴AC＝2，∵AB＝2AC，∴AB＝4，∴BD＝4﹣1＝3，∴BC＝＝＝2;②当△ABC是钝角三角形，如图2，同理得:AC＝2，AB＝4，∴BC＝＝＝2;综上所述，BC的长为2或2．故答案为:2或2．【点评】本题考查了三角形的高、勾股定理的应用，在直角三角形中常利用勾股定理计算线段的长，要熟练掌握．13．（4分）（2018•福建）把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB＝，则CD＝﹣1 ．【考点】勾股定理．【专题】11:计算题．【分析】先利用等腰直角三角形的性质求出BC＝2，BF＝AF＝1，再利用勾股定理求出DF，即可得出结论．【解答】解:如图，过点A作AF⊥BC于F，在Rt△ABC中，∠B＝45°，∴BC＝AB＝2，BF＝AF＝AB＝1，∵两个同样大小的含45°角的三角尺，∴AD＝BC＝2，在Rt△ADF中，根据勾股定理得，DF＝＝∴CD＝BF+DF﹣BC＝1+﹣2＝﹣1，故答案为:﹣1．【点评】此题主要考查了勾股定理，等腰直角三角形的性质，正确作出辅助线是解本题的关键．14．（4分）（2018•黄冈）如图，圆柱形玻璃杯高为14cm，底面周长为32cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为20 cm（杯壁厚度不计）．【考点】KV:平面展开﹣最短路径问题．【专题】27:图表型．【分析】将杯子侧面展开，建立A关于EF的对称点A′，根据两点之间线段最短可知A′B 的长度即为所求．【解答】解:如图:将杯子侧面展开，作A关于EF的对称点A′，连接A′B，则A′B即为最短距离，A′B＝＝＝20（cm）．故答案为20．【点评】本题考查了平面展开﹣﹣﹣最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．三、解答题:（每题11分，共计44分）15．（11分）一棵树在离地面9米处断裂，树的顶部落在离树根底部12米处，求树折断之前的高度？（自己画图并解答）【考点】勾股定理的应用．【分析】根据勾股定理，计算树的折断部分是15米，则折断前树的高度是15+9=24米．【解答】解:如图所示:因为AB=9米，AC=12米，根据勾股定理得BC==15米，于是折断前树的高度是15+9=24米．【点评】本题考查正确运用勾股定理．善于观察题目的信息是解题以及学好数学的关键．16．（11分）小东与哥哥同时从家中出发，小东以6km/时的速度向正北方向的学校走去，哥哥则以8km/时的速度向正东方向走去，半小时后，小东距哥哥多远？【考点】勾股定理的应用．【分析】根据题意求出小东与哥哥各自行走的距离，根据勾股定理计算即可．【解答】解:由题意得，AC=6×=3km，BC=8×=4km，∠ACB=90°，则AB==5km．【点评】本题考查的是勾股定理的应用，正确构造直角三角形、灵活运用勾股定理是解题的关键．17．（11分）如图所示，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，∠A=90°; （1）求BD的长;（2）求四边形ABCD的面积．【考点】勾股定理;勾股定理的逆定理．【分析】（1）在Rt△ABD中，利用勾股定理可求出BD的长度;（2）利用勾股定理的逆定理判断出△BDC为直角三角形，根据S四边形ABCD=S△ABD+S△BDC，即可得出答案．【解答】解:（1）∵∠A=90°，∴△ABD为直角三角形，则BD2=AB2+AD2=25，解得:BD=5．（2）∵BC=13cm，CD=12cm，BD=5cm，∴BD2+CD2=BC2，∴BD⊥CD，故S四边形ABCD=S△ABD+S△BDC=AB×AD+BD×DC=6+30=36．【点评】本题考查了勾股定理及勾股定理的逆定理，在求不规则图形的面积时，我们可以利用分解法，将不规则图形的面积转化为几个规则图形的面积之和．18．（11分）如图，有一个直角三角形纸片，两直角边AB=6cm，BC=8cm，现将直角边BC沿直线BD折叠，使点C落在点E处，求三角形BDF的面积是多少？【考点】翻折变换（折叠问题）．【专题】应用题;操作型．【分析】由折叠的性质得到三角形BDC与三角形BDE全等，进而得到对应边相等，对应角相等，再由两直线平行内错角相等，等量代换及等角对等边得到FD=FB，设FD=FB=xcm，则AF=（8﹣x）cm，在直角三角形AFB中，利用勾股定理列出关于x的方程，求出方程的解得到x 的值，确定出FD的长，进而求出三角形BDF面积．【解答】解:由折叠可得:△BDC≌△BDE，∴∠CBD=∠EBD，BC=BE=8cm，ED=DC=AB=6cm，∵AD∥BC，∴∠ADB=∠DBC，∴∠ADB=∠EBD，∴FD=FB，设FD=FB=xcm，则有AF=AD﹣FD=（8﹣x）cm，在Rt△ABF中，根据勾股定理得:x2=（8﹣x）2+62，解得:x=，即FD=cm，则S△BDF=FD•AB=cm2．【点评】此题考查了翻折变换（折叠问题），涉及的知识有:折叠的性质，全等三角形的性质，平行线的性质，等腰三角形的判定，以及勾股定理，熟练掌握性质及定理是解本题的关键．四、附加题19．如图所示的一块地，AD=12m，CD=9m，∠ADC=90°，AB=39m，BC=36m，求这块地的面积．【考点】勾股定理的应用;三角形的面积;勾股定理的逆定理．【专题】应用题．【分析】连接AC，运用勾股定理逆定理可证△ACD，△ABC为直角三角形，可求出两直角三角形的面积，此块地的面积为两个直角三角形的面积差．【解答】解:连接AC，则在Rt△ADC中，AC2=CD2+AD2=122+92=225，∴AC=15，在△ABC中，AB2=1521，AC2+BC2=152+362=1521，∴AB2=AC2+BC2，∴∠ACB=90°，∴S△ABC﹣S△ACD=AC•BC﹣AD•CD=×15×36﹣×12×9=270﹣54=216．答:这块地的面积是216平方米．【点评】解答此题的关键是通过作辅助线使图形转化成特殊的三角形，可使复杂的求解过程变得简单．20．如图，△ABC是直角三角形，∠BAC=90°，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF．（1）如图1，试说明BE2+CF2=EF2;（2）如图2，若AB=AC，BE=12，CF=5，求△DEF的面积．【考点】全等三角形的判定与性质;勾股定理;等腰直角三角形．【分析】（1）延长ED至点G，使得EG=DE，连接FG，CG，易证EF=FG和△BDE≌△CDG，可得BE=CG，∠DCG=∠DBE，即可求得∠FCG=90°，根据勾股定理即可解题;（2）连接AD，易证∠ADE=∠CDF，即可证明△ADE≌△CDF，可得AE=CF，BE=AF，S四边形AEDF=S △ABC，再根据△DEF的面积=S△ABC﹣S△AEF，即可解题．【解答】（1）证明:延长ED至点G，使得DG=DE，连接FG，CG，∵DE=DG，DF⊥DE，∴DF垂直平分DE，∴EF=FG，∵D是BC中点，∴BD=CD，在△BDE和△CDG中，，∴△BDE≌△CDG（SAS），∴BE=CG，∠DCG=∠DBE，∵∠ACB+∠DBE=90°，∴∠ACB+∠DCG=90°，即∠FCG=90°，∵CG2+CF2=FG2，∴BE2+CF2=EF2;（2）解:连接AD，∵AB=AC，D是BC中点，∴∠BAD=∠C=45°，AD=BD=CD，∵∠ADE+∠ADF=90°，∠ADF+∠CDF=90°，∴∠ADE=∠CDF，在△ADE和△CDF中，，∴△ADE≌△CDF（ASA），∴AE=CF，BE=AF，AB=AC=17，∴S四边形AEDF=S△ABC，∴S△AEF=×5×12=30，∴△DEF的面积=S△ABC﹣S△AEF=．【点评】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△BDE≌△CDG和△ADE≌△CDF是解题的关键．。

第二章 勾股定理与平方根 单元测试一、填空题1、下列和数1415926.3)1( .3.0)2( 722)3( 2)4( 38)5(-2)6(π (3030030003).0)7( 其中无理数有________，有理数有________（填序号） 2、94的平方根________，216.0的立方根________。

3、16的平方根________，64的立方根________。

4、算术平方根等于它本身的数有________，立方根等于本身的数有________。

5、若2562=x ，则=x ________，若2163-=x ，则=x ________。

6、已知ABC Rt ∆两边为3，4，则第三边长________。

7、若三角形三边之比为3：4：5，周长为24，则三角形面积________。

8、已知三角形三边长n n n n n n ,122,22,1222++++为正整数，则此三角形是________三角形。

9、如果0)6(42=++-y x ，则=+y x ________。

10、如果12-a 和-5是一个数m 的平方根，则.__________,==m a11、三角形三边分别为8，15，17，那么最长边上的高为________。

12、直角三角形三角形两直角边长为3和4，三角形内一点到各边距离相等，那么这个距离为________。

二、选择题13、下列几组数中不能作为直角三角形三边长度的是（ ） A 25,24,6===c b a B 5.2,2,5.1===c b a C 45,2,32===c b aD 17,8,15===c b a14、小强量得家里彩电荧屏的长为cm 58，宽为cm 46，则这台电视机尺寸是（ ） A 9英寸（cm 23） B 21英寸（cm 54） C 29英寸（cm 74） D 34英寸（cm 87） 15、等腰三角形腰长cm 10，底边cm 16，则面积（ ） A 296cmB 248cmC 224cmD 232cm16、三角形三边c b a ,,满足ab c b a 2)(22+=+，则这个三角形是（ ） A 锐角三角形B 钝角三角形C 直角三角形D 等腰三角形17、2)6(-的平方根是（ ） A 6-B 36C ±6D 6±18、下列命题正确的个数有：a a a a==233)2(,)1(（3）无限小数都是无理数（4）有限小数都是有理数（5）实数分为正实数和岁实数两类（ ） A 1个 B 2个 C 3个D 4个19、x 是2)9(-的平方根，y 是64的立方根，则=+y x （ ） A 3 B 7 C 3，7 D 1，7 20、直角三角形边长度为5，12，则斜边上的高（ ） A 6B 8C1318 D136021、直角三角形边长为b a ,，斜边上高为h ，则下列各式总能成立的是（ ） A 2h ab =B 2222h b a =+ Chb a 111=+ D222111hba=+22、如图一直角三角形纸片，两直角边cm BC cm AC 8,6==，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（ ） A cm 2 B cm 3 C cm 4 D cm 5 三、计算题23、求下列各式中x 的值04916)1(2=-x 25)1)(2(2=-x8)2)(3(3-=x27)3()4(3=--x四、作图题 25、在数轴上画出8-的点。