小形变时杨氏模量等于三倍的剪切模量

什么是杨氏模量和切变模量杨氏模量和切变模量是用来描述物质力学性质的两个重要参数。

本文将详细介绍杨氏模量和切变模量的定义、计算方法以及它们在材料科学和工程领域的应用。

一、杨氏模量1. 定义杨氏模量（Young's modulus），也称为弹性模量，是材料在拉伸力作用下的应力与应变之比，用来描述材料的拉伸性能。

它代表了单位截面积的材料在垂直于应力方向上发生变形的能力。

2. 计算方法杨氏模量的计算公式为：E = (F/A)/(ΔL/L0)其中，E为杨氏模量，F为作用在材料上的拉伸力，A为材料截面积，ΔL为材料在拉伸力作用下的长度变化，L0为原始长度。

3. 应用杨氏模量是材料工程中最常用的力学参数之一，可以用来评估材料的抗拉性能。

在实际应用中，杨氏模量被广泛用于材料的设计和选用，例如钢铁、混凝土、聚合物等。

此外，杨氏模量还可以用于计算材料的应力分布、变形和弹性恢复等。

二、切变模量1. 定义切变模量（Shear modulus），也称为剪切模量或刚性模量，是材料在剪切力作用下的应力与应变之比，用来描述材料的扭转性能。

它代表了单位截面积的材料在剪切力作用下发生变形的阻力。

2. 计算方法切变模量的计算公式为：G = (F/A)/(θ/t)其中，G为切变模量，F为作用在材料上的剪切力，A为材料截面积，θ为材料受到的扭转角度，t为材料的厚度。

3. 应用切变模量是描述材料的剪切性能的重要参数。

在材料工程和结构设计中，切变模量常常被用来计算材料的刚性和扭转变形。

例如，在金属加工中，切变模量可以用来评估材料的切削特性和切削力。

此外，切变模量还被广泛应用于复合材料、土力学等领域。

总结：杨氏模量和切变模量是描述材料力学性能的两个重要参数。

杨氏模量用于描述材料的拉伸性能，而切变模量用于描述材料的扭转性能。

它们的计算公式分别为F/A)/(ΔL/L0)和(F/A)/(θ/t)。

在工程实践中，杨氏模量和切变模量被广泛应用于材料选择、结构设计、材料加工等领域，对于改善产品性能和优化工艺具有重要意义。

杨氏模量和剪切模量的关系杨氏模量(Young’sModulus)和剪切模量(ShearModulus)的关系是力学中一个重要的课题。

它们之间的关系影响着材料的机械性能，这对科学家来说非常重要。

在19世纪早期，多位物理学家试图研究这种关系。

在探索固体物理学，材料学和金属材料等方面，利用定理可以建立杨氏模量和剪切模量之间的关系。

一、杨氏模量杨氏模量是指当某种物体在一个拉伸力作用下，其体积不变，但长度发生变化时，所产生的拉伸刚度和对应的应变比率。

它可以用来描述物体的刚度和机械性能。

它是由爱因斯坦在20世纪初提出的一个基本定理，由英国物理学家，杨利伯博士在1807发现，因此而得名。

二、剪切模量剪切模量是一种应变，是物体在作用于其水平表面时产生的应变，这种应变和作用力的方向成90度，也被称为剪切应变。

它是一种衡量物体的刚度的尺度，可以用于区分不同的材料。

三、杨氏模量与剪切模量的关系在力学中，杨氏模量和剪切模量是相关的。

他们之间的关系可以通过公式来表示：G=E/3(1-2v)，其中G表示剪切模量，E表示杨氏模量，v表示泊松比。

从这个公式中可以看出，当E和v都是常数时，杨氏模量与剪切模量之间存在固定的关系，也就是G=E/3(1-2v)。

材料的弹性模量是由两个模量的乘积决定的，也就是E×G，它决定了材料在弹性变形时的变形程度。

剪切模量与杨氏模量之间的关系可以使我们比较材料的机械性能和刚度。

例如，在给定单位应力下，当杨氏模量大于剪切模量时，表明材料更倾向于发生拉伸性变形，而当剪切模量大于杨氏模量时，表明材料更倾向于发生剪切性变形。

四、实验研究杨氏模量和剪切模量的关系的研究，已有多位物理学家做出重要的贡献。

爱因斯坦认为，二者之间可以建立一定的关系，其结果被用来建立了杨氏模量和剪切模量之间的相互关系，也就是G=E/3(1-2v)。

除此之外，拉米特，马斯基，瓦特等物理学家也研究了杨氏模量与剪切模量之间的关系，并做出了贡献。

杨氏栈量的测量卖脸讲义测量金属丝的杨氏模量力作用于物体所引起的效果之一是使受力物体发生形变，物体的形变可分为弹性形变和塑性形 变。

固体材料的弹性形变又可分为纵向、切变、扭转、弯曲，对于纵向弹性形变可以引入杨氏模量 来描述材料抵抗形变的能力。

杨氏模量是表征固体材料性质的一个重要的物理量，是工程设计上选 用材料时常需涉及的重要参数之一，一般只与材料的性质和温度有关，与其几何形状无关。

实验测定杨氏模量的方法很多，如拉伸法、弯曲法和振动法（前两种方法属静态法，后一种属 动态法）。

当前更多的是用拉伸法测定金属丝的杨氏模量，它提供了测量微小长度的方法，既有光杠杆法, 也有显微镜法。

本仪器采用光杠杆法。

实验目的1.学会用拉伸法测量金属丝的杨氏模量 2.掌握光杠杆法测量微小伸长量的原理 3.掌握各种测量工具的正确使用方法 4.学会用逐差法或最小二乘法处理实验数据 5. 学会不确定度的计算方法，结果的正确表达实验原理杨氏模量的定义设金属丝的原长为乙横截面积为S,沿长度方向施力F 后，其长度改变△厶，则金属丝单位面积 上受到的垂直作用力“F/S 称为正应力，金属丝的相对伸长量戸△£/厶称为线应变。

实验结果指出，在 弹性范围内，由胡克定律可知物体的正应力与线应变成正比，即：a=E £（1）或—=£•— （2） S L比例系数£即为金属丝•的杨氏模量（单位：Pa 或N/m 2）,它表征材料本身的性质，E 越犬的材料, 要使它发生一定的相对形变所需要的单位横截面积上的作用力也越大。

由式（2）可知：(3)对于直径为d 的圆柱形金属丝，其杨氏模量为:式中厶（金属丝原长）可由卷尺测量，d （金属幺纟直径）可用螺旋测微器测量，F （外力）可由 实验中数字拉力计上显示的质量加求出，即尸=〃农（g 为重力加速度），而△厶是一个微小长度变化（mm 级）。

针对△厶的测量方法，本实验仪采用光杠杆法。

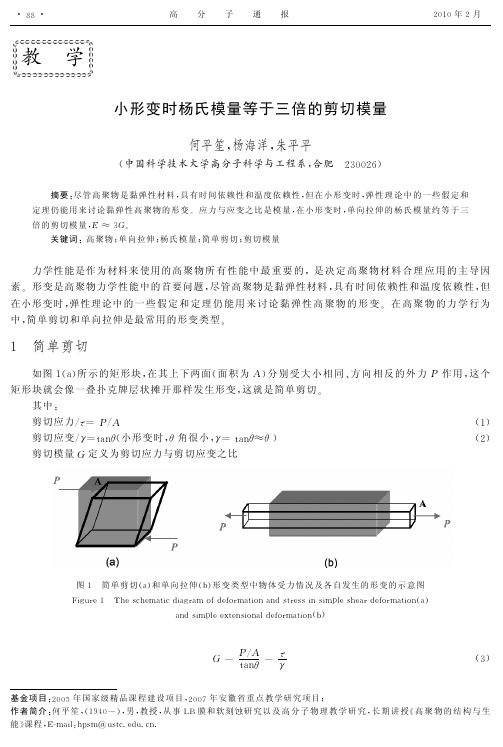
基金项目!!""&年国家级精品课程建设项目!!""$年安徽省重点教学研究项目"作者简介!何平笙!##)%"b $!男!教授!从事E P 膜和软刻蚀研究以及高分子物理教学研究!长期讲授%高聚物的结构与生能&课程!S J M ;0?’<>:M "################$$$$C :64a 3=C a 45a T !.小形变时杨氏模量等于三倍的剪切模量89:!(k ;!o 99!+,-.$%8.#<=-.9:;>"Po !!-""!(#!!摘要!尽管高聚物是黏弹性材料!具有时间依赖性和温度依赖性!但在小形变时!弹性理论中的一些假定和定理仍能用来讨论黏弹性高聚物的形变(应力与应变之比是模量!在小形变时!单向拉伸的杨氏模量约等于三倍的剪切模量!@1-?(!!关键词!高聚物"单向拉伸"杨氏模量"简单剪切"剪切模量力学性能是作为材料来使用的高聚物所有性能中最重要的!是决定高聚物材料合理应用的主导因素(形变是高聚物力学性能中的首要问题!尽管高聚物是黏弹性材料!具有时间依赖性和温度依赖性!但在小形变时!弹性理论中的一些假定和定理仍能用来讨论黏弹性高聚物的形变(在高聚物的力学行为中!简单剪切和单向拉伸是最常用的形变类型(#!<-=>如图##;$所示的矩形块!在其上下两面#面积为+$分别受大小相同)方向相反的外力0作用!这个矩形块就会像一叠扑克牌层状摊开那样发生形变!这就是简单剪切(其中’剪切应力*.i 0*+##$剪切应变*/i 6;50#小形变时!0角很小!/i 6;5010$#!$!!剪切模量?定义为剪切应力与剪切应变之比图#!简单剪切#;$和单向拉伸#N $形变类型中物体受力情况及各自发生的形变的示意图\09C 73#!,<3:4<3M ;604=0;97;M8@=3@87M ;6085;5=:673::05:0M >?3:<3;7=3@87M ;6085#;$;5=:0M >?33D 635:085;?=3@87M ;6085#N $?K0*+6;50K ./#-$!!模量的倒数是柔量!剪切柔量W i #"?#如果在剪切应力作用下物体完全不改变形状!则0i 6;50("!?(t #因此!剪切模量?是物体刚性的度量!?越大!材料越刚硬!形状改变就越不容易#简单剪切的特点是$%#&只有物体形状的变化!而体积保持不变’%!&对分子运动特别敏感’%-&可以容易地把高聚物宏观力学性能与他们内部分子运动相联系!容易引入一些简化的假定!建立高聚物力学行为的分子理论’%%&能很好区分固体(液体及介于他们之间的任何中间状态的物体%黏弹体&!因此应用甚广’%&&容易实现#剪切形变可由多种方式来实现#如两对大小相等(正交的拉应力或压应力相当于两对剪切应力的作用’空心圆筒的扭转也产生剪切形变#!!-?@A图#%N &所示的长方棒!在其两个端头面+上受到两个大小相等方向相反的正向拉力0!则拉伸应力$i 0"+%%&!!拉伸应变"#K 1L 1"1"K 111"%棒从原长1"拉长到了1&%&&!!杨氏模量@i$"#%(&单向拉伸时!棒被拉长的同时!横截面会发生收缩%由%"!,"缩短为%!,&!则横向应变为和"!i%b %"%""-i,b ,",2-."%$&%’&!!定义横向收缩与纵向拉伸之比为泊松比&&KL "!"#KL "-"#%)&!!单向拉伸的特点是$%#&材料受拉时!其体积也发生了变化#一般来说!材料受拉时体积是增加的!因此&*"H &#如果拉伸时材料体积不变!&i "H&#橡胶和流体的&最接近"H &’%!&对大多数高聚物!拉伸时的体积变化相对于其形状改变来说是很小的#在&("H &时!有@1-?的近似关系#因此!由单向拉伸实验得到的资料可以与简单剪切实验得到的资料相比较’%-&拉伸实验非常容易实现!只要在试样两头加上拉力就可以实现单向拉伸#事实上!材料试验机通常就是指拉伸试验机!在即使是很小型的企业里也能找到它的踪影#-!B |U C (D O E @F=>O E ?8GH !@1-?%#&弹性力学早就推导出剪切模量?(杨氏模量@和泊松比&的关系是!?K @!%#O &&%#"&!!材料受拉时!在外形尺寸改变的同时它的体积也发生了变化#一般来说!当材料处于拉应力作用下其体积是增加的!此时泊松比&*"a &#如果拉伸时材料体积不变!则泊松比&i "a &#橡胶和流体的泊松比接近"k &!即他们拉伸时体积几乎不变#泊松比&("a &!则@1-?!!!!"如果再引用物体的本体模量>#它与杨氏模量@和泊松比&有关系#>K @-!#L !&"!##"联立!#""和!##"式#消去参数&#可得@K-?#O?->!#!"本体模量比剪切模量大很多#->比?大得更多#?$->3##因此#也可推得@1-?!!!-"再来看由交联橡胶推导的储能函数#S K?!!%!#O %!!O %!-L -"!#-"由储能函数可以求得交联橡胶任何形变类型的应力J应变关系#从而可以来验证杨氏模量和剪切模量之间的关系%对单向拉伸#一个本来是立方体的试样变成了一个长方体%如果拉伸比是%#i %#则其横向相应收缩#在体积不变条件下%!K %-K #$4%#所以拉力*为*K,S ,%K ?%L #%!"!K ?%#L #%!"-K ?%#L#!"%#O #%O #%!"!K ?#L #!"%%O #O #!"%!#%"式!#%"不是虎克定律的形式#拉伸时的虎克定律应该是$K @!%L #"!#&"!%G #"就是伸长百分比%因为应力是单位面积上的拉力#所以$i *$%!&%-i*&%#则*K @#L#!"%!#("在%(#时#即伸长很小时#式!#%"化简为*1-?#L #!"%!#$"比较式!#("与式!#$"#也得@1-?!!!当%(#时"这正是泊松比&K "H &时的情况%正如前面已经讲过的#不管是在大学和研究所的实验室还是在工厂和企业里#最常见的力学实验装置就是拉力试验机#从高聚物的拉伸图上可以得到很多有用的信息%事实上#高聚物的黏弹性理论大多是在与简单剪切有关的研究中发展起来的#但在实验和数据积累方面#又主要靠单向拉伸实验%拉伸实验得到的杨氏模量@与简单剪切实验得到的剪切模量?是如此简单的倍数关系给高聚物力学性能的研究带来很多方便%>?@A !’#(!何平笙a高聚物的力学性能a 第二版a 合肥)中国科学技术大学出版社#!""’a ’!(!马德柱#何平笙#徐种德#周漪琴a 高聚物的结构与性能a 第二版a 北京)科学出版社##))&a ’-(!何曼君#张红东#陈维孝#董西侠a 高分子物理a 第三版a 上海)复旦大学出版社#!""$a ’%(!何笙平a新编高聚物的结构与性能a 北京)科学出版社#!"")a-17?A!B.1D7F7B G B)C644)G R4B1H=C486.1D7F7B G?N469=R8F F\4H16R8@G1?O S*059J:<359"K+.L O;0J A;59"X OH*059J>059#M/P$’(2/!(&*0&1)2/’:.3/!./$!,@!=3!//’3!="B!3-/’53()&*:.3/!./$!,F/.9!&1&=)&*893!$"A/*/3!-""!("893!$$"5B@68>@%+?6<8C9<>8?A M370:;Z0:483?;:604M;6637Y06<60M3=3>35=3543;5=63M>37;6C73 =3>35=3543":8M3?;Y3:8@4?;::043?;:6046<387A;73:60??;N?368=0::4C::6<3=3@87M;60858@>8?A M37 Y06<Z0:483?;:60406A a,<3K8C59!:M8=C?C:05635:0850:6<73360M3:8@:<3;7M8=C?C:05:0M>?3:<3;7;: =3@87M;6085N3059Z37A:M;??"@1-?aK49L16D B%*8?A M37&,35:085&K8C59!:M8=C?C:&/0M>?3:<3;7&/<3;7M8=C?C:。

材料力学公式总结材料力学是研究材料在外力作用下的力学性质和行为的学科。

它的研究对象包括材料的强度、刚度、塑性变形、断裂等方面的性质。

材料力学公式是用来描述和计算材料力学性质的数学表达式。

下面是材料力学公式的总结。

1. 杨氏模量（Young's modulus）：杨氏模量是衡量材料刚度的指标，表示材料在拉伸或压缩过程中的应力和应变之比。

杨氏模量的计算公式为：E=σ/ε其中，E为杨氏模量，σ为应力，ε为应变。

2. 泊松比（Poisson's ratio）：泊松比是描述材料压缩应变时的纵向收缩和横向膨胀之间的比例关系。

泊松比的计算公式为：ν=-ε横向/ε纵向其中，ν为泊松比，ε横向为横向应变，ε纵向为纵向应变。

3. 斯特劳斯公式（Stress-Strain Curve）：斯特劳斯公式描述了材料的应力和应变之间的关系。

在弹性阶段，应力和应变线性相关，即：σ=E*ε其中，σ为应力，E为杨氏模量，ε为应变。

4. 屈服强度（Yield Strength）：屈服强度是材料在超过弹性极限后开始发生塑性变形的应力。

屈服强度一般用屈服点上的应力值表示。

5. 弹性极限（Elastic Limit）：弹性极限是指材料在不发生塑性变形的最大应力值。

超过弹性极限后，材料将开始发生塑性变形。

6. 拉伸强度（Tensile Strength）：拉伸强度是材料在拉伸过程中最大的抗拉应力，表示材料抵抗破坏的能力。

7. 断裂强度（Fracture Strength）：断裂强度是材料发生破裂时所承受的应力。

它是材料在强度和脆性方面的一个重要指标。

8. 斯特劳斯硬化指数（Strain Hardening Exponent）：斯特劳斯硬化指数描述了材料在塑性变形时硬度增加的速率。

该指数可以通过材料力学实验和测试获得。

9. 塑性应变（Plastic Strain）：塑性应变是材料在超过弹性极限后发生塑性变形的应变量。

10. 线膨胀系数（Linear Expansion Coefficient）：线膨胀系数描述了材料在温度变化下长度变化的比例关系。

杨氏模量各个值的单位杨氏模量，也称为剪切模量，是描述材料抵抗剪切变形的能力的物理常数。

它在各个领域的工程和科学中都有重要的应用，例如材料力学、建筑结构设计等。

本文将从不同的角度探讨杨氏模量的各个值及其单位，以期增加读者对杨氏模量的理解和应用。

第一节：引言杨氏模量是衡量材料刚度和弹性的重要指标之一。

它定义为材料在受力时单位面积内所产生的应力与应变之比，通常用符号E表示。

杨氏模量的值越大，表示材料越刚性，抵抗外力变形能力越强。

第二节：杨氏模量的定义及其单位杨氏模量的定义是单位应力下单位应变的比值。

在国际单位制中，杨氏模量的单位是帕斯卡（Pa），也可以用兆帕（MPa）表示。

1帕斯卡等于1牛顿/平方米，1兆帕等于1百万帕斯卡。

第三节：金属材料的杨氏模量金属材料常用的杨氏模量通常在100 GPa到400 GPa之间。

例如，钢的杨氏模量约为200 GPa，铝的杨氏模量约为70 GPa。

这些数值反映了金属材料在受力时的刚性和强度。

第四节：非金属材料的杨氏模量非金属材料的杨氏模量通常相对较小。

例如，木材的杨氏模量约为10 GPa到20 GPa，混凝土的杨氏模量约为30 GPa到50 GPa。

这些数值反映了非金属材料的柔韧性和适应性。

第五节：杨氏模量的影响因素杨氏模量的值受多种因素的影响，包括材料的组成、晶体结构、温度等。

不同的材料具有不同的杨氏模量，这也是它在工程设计中的重要参数之一。

在材料设计中，需要根据所需的刚性和强度来选择合适的材料。

第六节：杨氏模量的应用杨氏模量在工程和科学中有广泛的应用。

在建筑结构设计中，工程师需要根据材料的杨氏模量来计算和预测结构的变形和稳定性。

在材料力学研究中，科学家可以通过测量杨氏模量来研究材料的弹性和塑性行为。

第七节：结论杨氏模量是描述材料刚性和弹性的重要指标，它的值反映了材料在受力时的变形能力。

不同材料的杨氏模量有所差异，这使得我们可以根据需要选择合适的材料。

通过对杨氏模量的研究和应用，我们可以更好地理解和掌握材料的性能和行为。

基金项目!!""&年国家级精品课程建设项目!!""$年安徽省重点教学研究项目"作者简介!何平笙!##)%"b $!男!教授!从事E P 膜和软刻蚀研究以及高分子物理教学研究!长期讲授%高聚物的结构与生能&课程!S J M ;0?’<>:M "################$$$$C :64a 3=C a 45a T !.小形变时杨氏模量等于三倍的剪切模量89:!(k ;!o 99!+,-.$%8.#<=-.9:;>"Po !!-""!(#!!摘要!尽管高聚物是黏弹性材料!具有时间依赖性和温度依赖性!但在小形变时!弹性理论中的一些假定和定理仍能用来讨论黏弹性高聚物的形变(应力与应变之比是模量!在小形变时!单向拉伸的杨氏模量约等于三倍的剪切模量!@1-?(!!关键词!高聚物"单向拉伸"杨氏模量"简单剪切"剪切模量力学性能是作为材料来使用的高聚物所有性能中最重要的!是决定高聚物材料合理应用的主导因素(形变是高聚物力学性能中的首要问题!尽管高聚物是黏弹性材料!具有时间依赖性和温度依赖性!但在小形变时!弹性理论中的一些假定和定理仍能用来讨论黏弹性高聚物的形变(在高聚物的力学行为中!简单剪切和单向拉伸是最常用的形变类型(#!<-=>如图##;$所示的矩形块!在其上下两面#面积为+$分别受大小相同)方向相反的外力0作用!这个矩形块就会像一叠扑克牌层状摊开那样发生形变!这就是简单剪切(其中’剪切应力*.i 0*+##$剪切应变*/i 6;50#小形变时!0角很小!/i 6;5010$#!$!!剪切模量?定义为剪切应力与剪切应变之比图#!简单剪切#;$和单向拉伸#N $形变类型中物体受力情况及各自发生的形变的示意图\09C 73#!,<3:4<3M ;604=0;97;M8@=3@87M ;6085;5=:673::05:0M >?3:<3;7=3@87M ;6085#;$;5=:0M >?33D 635:085;?=3@87M ;6085#N $?K0*+6;50K ./#-$!!模量的倒数是柔量!剪切柔量W i #"?#如果在剪切应力作用下物体完全不改变形状!则0i 6;50("!?(t #因此!剪切模量?是物体刚性的度量!?越大!材料越刚硬!形状改变就越不容易#简单剪切的特点是$%#&只有物体形状的变化!而体积保持不变’%!&对分子运动特别敏感’%-&可以容易地把高聚物宏观力学性能与他们内部分子运动相联系!容易引入一些简化的假定!建立高聚物力学行为的分子理论’%%&能很好区分固体(液体及介于他们之间的任何中间状态的物体%黏弹体&!因此应用甚广’%&&容易实现#剪切形变可由多种方式来实现#如两对大小相等(正交的拉应力或压应力相当于两对剪切应力的作用’空心圆筒的扭转也产生剪切形变#!!-?@A图#%N &所示的长方棒!在其两个端头面+上受到两个大小相等方向相反的正向拉力0!则拉伸应力$i 0"+%%&!!拉伸应变"#K 1L 1"1"K 111"%棒从原长1"拉长到了1&%&&!!杨氏模量@i$"#%(&单向拉伸时!棒被拉长的同时!横截面会发生收缩%由%"!,"缩短为%!,&!则横向应变为和"!i%b %"%""-i,b ,",2-."%$&%’&!!定义横向收缩与纵向拉伸之比为泊松比&&KL "!"#KL "-"#%)&!!单向拉伸的特点是$%#&材料受拉时!其体积也发生了变化#一般来说!材料受拉时体积是增加的!因此&*"H &#如果拉伸时材料体积不变!&i "H&#橡胶和流体的&最接近"H &’%!&对大多数高聚物!拉伸时的体积变化相对于其形状改变来说是很小的#在&("H &时!有@1-?的近似关系#因此!由单向拉伸实验得到的资料可以与简单剪切实验得到的资料相比较’%-&拉伸实验非常容易实现!只要在试样两头加上拉力就可以实现单向拉伸#事实上!材料试验机通常就是指拉伸试验机!在即使是很小型的企业里也能找到它的踪影#-!B |U C (D O E @F=>O E ?8GH !@1-?%#&弹性力学早就推导出剪切模量?(杨氏模量@和泊松比&的关系是!?K @!%#O &&%#"&!!材料受拉时!在外形尺寸改变的同时它的体积也发生了变化#一般来说!当材料处于拉应力作用下其体积是增加的!此时泊松比&*"a &#如果拉伸时材料体积不变!则泊松比&i "a &#橡胶和流体的泊松比接近"k &!即他们拉伸时体积几乎不变#泊松比&("a &!则@1-?!!!!"如果再引用物体的本体模量>#它与杨氏模量@和泊松比&有关系#>K @-!#L !&"!##"联立!#""和!##"式#消去参数&#可得@K-?#O?->!#!"本体模量比剪切模量大很多#->比?大得更多#?$->3##因此#也可推得@1-?!!!-"再来看由交联橡胶推导的储能函数#S K?!!%!#O %!!O %!-L -"!#-"由储能函数可以求得交联橡胶任何形变类型的应力J应变关系#从而可以来验证杨氏模量和剪切模量之间的关系%对单向拉伸#一个本来是立方体的试样变成了一个长方体%如果拉伸比是%#i %#则其横向相应收缩#在体积不变条件下%!K %-K #$4%#所以拉力*为*K,S ,%K ?%L #%!"!K ?%#L #%!"-K ?%#L#!"%#O #%O #%!"!K ?#L #!"%%O #O #!"%!#%"式!#%"不是虎克定律的形式#拉伸时的虎克定律应该是$K @!%L #"!#&"!%G #"就是伸长百分比%因为应力是单位面积上的拉力#所以$i *$%!&%-i*&%#则*K @#L#!"%!#("在%(#时#即伸长很小时#式!#%"化简为*1-?#L #!"%!#$"比较式!#("与式!#$"#也得@1-?!!!当%(#时"这正是泊松比&K "H &时的情况%正如前面已经讲过的#不管是在大学和研究所的实验室还是在工厂和企业里#最常见的力学实验装置就是拉力试验机#从高聚物的拉伸图上可以得到很多有用的信息%事实上#高聚物的黏弹性理论大多是在与简单剪切有关的研究中发展起来的#但在实验和数据积累方面#又主要靠单向拉伸实验%拉伸实验得到的杨氏模量@与简单剪切实验得到的剪切模量?是如此简单的倍数关系给高聚物力学性能的研究带来很多方便%>?@A !’#(!何平笙a高聚物的力学性能a 第二版a 合肥)中国科学技术大学出版社#!""’a ’!(!马德柱#何平笙#徐种德#周漪琴a 高聚物的结构与性能a 第二版a 北京)科学出版社##))&a ’-(!何曼君#张红东#陈维孝#董西侠a 高分子物理a 第三版a 上海)复旦大学出版社#!""$a ’%(!何笙平a新编高聚物的结构与性能a 北京)科学出版社#!"")a-17?A!B.1D7F7B G B)C644)G R4B1H=C486.1D7F7B G?N469=R8F F\4H16R8@G1?O S*059J:<359"K+.L O;0J A;59"X OH*059J>059#M/P$’(2/!(&*0&1)2/’:.3/!./$!,@!=3!//’3!="B!3-/’53()&*:.3/!./$!,F/.9!&1&=)&*893!$"A/*/3!-""!("893!$$"5B@68>@%+?6<8C9<>8?A M370:;Z0:483?;:604M;6637Y06<60M3=3>35=3543;5=63M>37;6C73 =3>35=3543":8M3?;Y3:8@4?;::043?;:6046<387A;73:60??;N?368=0::4C::6<3=3@87M;60858@>8?A M37 Y06<Z0:483?;:60406A a,<3K8C59!:M8=C?C:05635:0850:6<73360M3:8@:<3;7M8=C?C:05:0M>?3:<3;7;: =3@87M;6085N3059Z37A:M;??"@1-?aK49L16D B%*8?A M37&,35:085&K8C59!:M8=C?C:&/0M>?3:<3;7&/<3;7M8=C?C:。

杨氏模量剪切模量和体积模量的关系下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!杨氏模量剪切模量和体积模量的关系引言杨氏模量（Young's modulus）、剪切模量（Shear modulus）和体积模量（Bulk modulus）是描述物质力学性质的重要参数，在材料科学和工程领域中具有广泛的应用。

弹性力学中的杨氏模量和切变模量杨氏模量和切变模量是弹性力学中两个重要的参数，它们描述了材料在受力下的变形行为。

本文将从理论原理、实验方法和应用等方面探讨杨氏模量和切变模量。

一、杨氏模量的介绍杨氏模量（Young's modulus）是描述材料在拉伸应力作用下的变形程度的物理量。

它是杨氏拉伸应力（单位面积的内部力）与引起该应力的拉伸应变（单位长度的伸长量）之比。

杨氏模量的单位是帕斯卡（Pa）。

杨氏模量的计算公式为：E = σ/ε其中，E为杨氏模量，σ为材料的拉伸应力，ε为材料的拉伸应变。

二、杨氏模量的测量方法1. 伸长法伸长法是一种常用的测量杨氏模量的方法。

该方法基于材料在受力下的伸长量与拉伸应力成正比的原理，通过施加不同大小的拉伸力，测量材料的伸长量，进而计算杨氏模量。

2. 悬臂梁法悬臂梁法是另一种常用的测量杨氏模量的方法。

该方法使用一个细长的杆状样品，将其一端固定在支架上，另一端悬空。

施加力矩使样品产生弯曲，通过测量弯曲量与施加力矩的关系，可以计算出杨氏模量。

三、切变模量的介绍切变模量（Shear modulus）是描述材料在剪切应力作用下的变形程度的物理量。

它是切变应力（单位面积的内部力）与引起该应力的剪切应变（单位长度的变形量）之比。

切变模量的单位也是帕斯卡（Pa）。

切变模量的计算公式为：G = τ/γ其中，G为切变模量，τ为材料的切变应力，γ为材料的切变应变。

四、切变模量的测量方法1. 平板扭转法平板扭转法是一种常用的测量切变模量的方法。

该方法在一块平板样品上施加扭转力矩，通过测量扭转角与施加力矩的关系，可以计算出切变模量。

2. 平行柱法平行柱法是另一种常用的测量切变模量的方法。

该方法使用两个平行的柱状样品，施加剪切力，在样品上产生变形，通过测量变形量与施加力的关系，可以计算出切变模量。

五、杨氏模量和切变模量的应用杨氏模量和切变模量是研究材料力学性质的重要参数，对于材料工程、土木工程等领域具有重要意义。

弹性力学中的杨氏模量与切变模量分析弹性力学是研究材料在力的作用下产生形变，并且在力停止作用后能够恢复原状的一门科学。

在弹性力学理论中，杨氏模量和切变模量是两个重要的物理量，它们描述了材料在受力时的特性和性能。

本文将从理论和应用两个角度，对杨氏模量和切变模量进行深入的分析。

一、杨氏模量的定义和意义杨氏模量（Young's modulus），又称弹性模量，是衡量材料抵抗拉伸形变能力的重要物理量。

它以符号E表示，定义为单位面积受力下单位长度的形变产生的应力。

杨氏模量可以用于描述材料的刚度，数值越大表示材料的刚度越高，即材料抗拉性能越好。

杨氏模量在实际应用中具有广泛的意义。

例如，在工程设计中，了解材料的杨氏模量可以帮助工程师选择适当的材料类型和尺寸。

另外，杨氏模量还可以用于预测结构在受外力作用下的变形和应力分布，对于确保结构的安全性和稳定性至关重要。

二、切变模量的定义和意义切变模量（Shear modulus），又称剪切模量或逆应变模量，是衡量材料抵抗剪切形变能力的重要物理量。

它以符号G表示，定义为单位面积受力下单位长度的剪切形变产生的剪切应力。

切变模量可以用于描述材料的柔软性，数值越大表示材料的柔软性越低，即材料的剪切性能越好。

切变模量在工程和科学研究中也有广泛的应用。

在土木工程领域，了解土壤的切变模量可以帮助工程师设计稳定的地基和基础结构。

在材料科学领域，切变模量的测量可以为新材料的研发和优化提供重要的数据。

三、杨氏模量与切变模量的关系杨氏模量与切变模量之间存在一定的关系，可以通过这个关系来相互换算。

这个关系由弹性理论中的泊松比定义出来，泊松比（Poisson's ratio）是用来描述材料体积变形时横向形变与纵向形变的比值。

杨氏模量E、切变模量G和泊松比ν之间的关系可以用以下公式表示：E = 2G(1 + ν)G = E / (2(1 + ν))通过这个公式，我们可以在已知杨氏模量或切变模量的情况下，计算出其它两个物理量的数值。