【K12教育学习资料】[学习]2018年七年级升八年级数学 暑期衔接班讲义 第五讲 专题一 三角形题

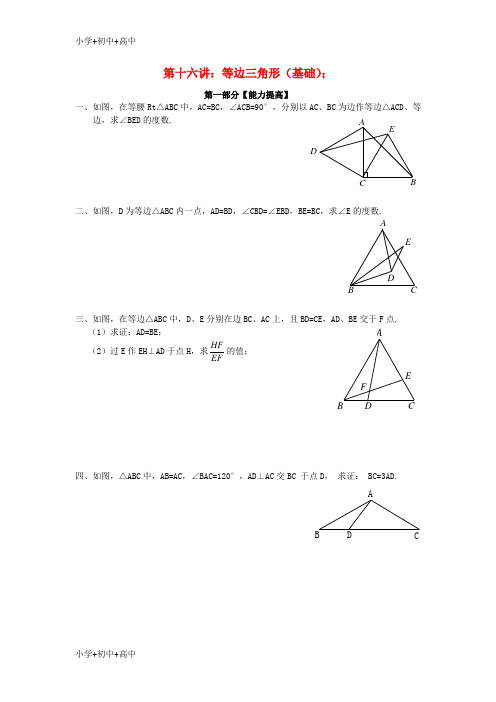
AC B E FD D CA B 第十六讲：等边三角形（基础）；第一部分【能力提高】一、如图，在等腰Rt △ABC 中，AC=BC ，∠ACB=90°，分别以AC 、BC 为边作等边△ACD 、等边，求∠BED 的度数.二、如图，D 为等边△ABC 内一点，AD=BD ，∠CBD=∠EBD ，BE=BC ，求∠E 的度数.三、如图，在等边△ABC 中，D 、E 分别在边BC 、AC 上，且BD=CE ，AD 、BE 交于F 点.（1）求证：AD=BE ； （2）过E 作EH ⊥AD 于点H ，求HF EF的值；四、如图，△ABC 中，AB=AC ，∠BAC=120°，AD ⊥AC 交BC•于点D ，•求证：•BC=3AD.A B C D E A D EAC B ED A C B ED五、如图，已知∠ABC=90°，△ABE 是等边三角形，点P 为射线BC 上任意一点（点P 与点B不重合），连结AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结QE 并延长交射线BC 于点F ，当点P 在BC 上运动时，猜想∠QFC 的度数是否改变？证明你的结论.六、如图，等边△ABC 中，D 为AC 的中点，E 为BC 延长线上一点，DB=DE.（1）求证：AD=CE ；（2）若D 为AC 边上任意的一点，其它条件不变，（1）中的结论是否仍然成立？证明你的结论.AC B P A C B P AC B P A第二部分【综合运用】七、（1）如图，等边△ABC ，P 为形外一点，∠BPC=120°.求证：①∠APB=∠APC=60°；②PB+PC+PA.（2）如图，等边△ABC ，P 为形外一点，∠APB=60°. 求证：①∠APC=60°；②PB+PC+PA.（3）如图，等边△ABC ，P 为形外一点，AP 平分∠BPC. 求证：①∠APB=∠APC=60°；②PB+PC+PA.（4）如图，在△ABC 中，∠BAC=60°，P 为形外一点，∠APB=∠APC=60°. 求证：①△ABC 为等边三角形；②PB+PC+PA.AC B P AC B PBD C A（5）如图，等腰△ABC 中，AB=AC ，P 为形外一点，∠APB=∠APC=60°. 求证：①△ABC 为等边三角形；②PB+PC+PA.（6）如图，在△ABC 中，∠ABC=60°，P 为形外一点，∠APB=∠APC=60°. 求证：①△ABC 为等边三角形；②PB+PC+PA.第 16 讲 作 业一．选择题1．下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；•③三个外角（每个顶点处各取一个外角）都相等的三角形；•④一腰上的中线也是这条腰上的高的等腰三角形．其中能判定该三角形是等边三角形的有( ).(A)①②③ (B)①②④ (C)①③ (D)①②③④2．已知直角三角形中30°角所对的直角边为2㎝，则斜边的长为( ).(A)2 ㎝ (B)4 ㎝ (C)6 ㎝ (D)8㎝3．Rt △ABC 中，CD 是斜边AB 上的高，∠B=30°，AD=2cm ，则AB 的长度是( ).(A)2cm (B)4cm (C)8cm (D)16cm4. 在△ABC 中，∠B=30°，∠C=45°，AD ⊥BC 于D ，CD=2CM ，则AB 长为( ). (A)2cm (B)3cm (C)4cm (D)5cm 5．如图，Rt △ABC 中，∠A=30°，BD 平分∠ABC ，若AD=8，则CD=( ).(A)2cm (B)3cm (C)4cm (D)5cm 6．等腰三角形一腰上的高等于该三角形某一条边的长度的一半，则其顶角等于( ).(A)30° (B)30°或150° (C)120°或150° (D)30°或120°或150°二．填空题A PB M E F N D 21AC B ED BE D C A AE D C B D C A B 7．△ABC 中，∠B=∠C=15°，AB=2cm ，CD ⊥AB 交BA 的延长线于点D ，•则CD•的长度是_______．8．如图C 为线段AB 上的一点，分别以AC 、BC 为边在AB 的同侧作等边△ACD 和等边△BCE ，连结CD ，且CD ⊥DE ，若AB=9，则AC=_______．9．如图，△ABC 中，AB=AC ，∠A=120°，AB 的垂直平分线交BC 于D ，若BC=12，则DE=_______．10．如图，等边△ABC 中，AC=9，AO=3，P 为AB 上的一个动点，将线段OP 绕O 点逆时针顺序旋转60°得到线段OQ ，要使点落在BC 上，则AP 的长为_______． 三、解答题11．如图，D 、E 、F 分别在等边△ABC 的三边上，且AD=BE=CF ，求证：△DEF•为等边三角形.12．如图，D 、E 、F 分别是等边△ABC 各边上的点，且AD=BE=CF ，连接AF 、BD 、CE 分别交于M 、N 、P 三点，求证：△PMN 为等边三角形.13．如图，E 是等边△ABC 中AC 边上的点，∠1=∠2，BE=CD ，求证：△ADE 为等边三角形.14. 如图，△ABC 中，AB=AC ，∠BAC=120°，AD ⊥AC 交BC•于点D ，•求证：•BC=3AD.。

第一部分——温故知新专题一 整式运算1.由数字与字母 组成的代数式叫做单项式。

单独一个数或字母也是单项式。

单项式中的 叫做单项式的系数单项式中所有字母的 叫做单项式的次数2.几个单项式的和叫做多项式多项式中 叫做这个多项式的次数3.单项式和多项式统称为4.整式加减实质就是 后5.同底数幂乘法法则：n m n m a a a +=·（m.n 都是正整数）；逆运算=+n m a 6.幂的乘方法则：()=n m a （m.n 都是正整数）；逆运算=mn a 7.积的乘方法则：()=n ab （n 为正整数）；逆运算=nn b a 8.同底数幂除法法则：n m n m a a a -=÷（a ≠0，m.n 都是正整数）；逆运算=-n m a9.零指数的意义：()010≠=a a ；10.负指数的意义：()为正整数p a aa p p ,01≠=- 11.整式乘法：（1）单项式乘以单项式；（2）单项式乘以多项式；（3）多项式乘以多项式12.整式除法：（1）单项式除以单项式；（2）多项式除以单项式知识点1.单项式多项式的相关概念归纳：在准确记忆基本概念的基础上，加强对概念的理解，并灵活的运用例1.下列说法正确的是（ ）A ．没有加减运算的式子叫单项式 B.35ab π-的系数是35- C.单项式-1的次数是0 D.3222+-ab b a 是二次三项式例2.如果多项式()1132+---x n xm 是关于x 的二次二项式，求m ，n 的值知识点2.整式加减归纳：正确掌握去括号的法则，合并同类项的法则例3.多项式()⎪⎭⎫ ⎝⎛-+--8313322xy ykxy x 中不含xy 项，求k 的值知识点3.幂的运算归纳：幂的运算一般情况下，考题的类型均以运算法则的逆运算为主，加强对幂的逆运算的练习，是解决这类题型的核心方法。

例4.已知5,3==n m a a求（1）n m a 32+的值 （2）n m a 23+的值例5.计算 （1）20102011324143⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛- （2）()1012201021---+⎪⎭⎫ ⎝⎛π知识点4.整式的混合运算归纳：整式的乘法法则和除法法则是整式运算的依据，注意运算时灵活运用法则。

三角形第一讲与三角形有关的线段1.定义：不在一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

注意：三条线段必须①不在一条直线上，②首尾顺次相接。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC.三角形ABC的顶点C所对的边AB可用c 表示,顶点B所对的边AC可用b表示,顶点A所对的边BC可用a表示.2.三角形三边的不等关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边。

3.三角形的高：从三角形的向它的作垂线，顶点和垂足之间的线段叫做三角形的高,（注意八字形）注意：高与垂线不同，高是线段，垂线是直线。

三角形的三条高相交于一点。

．．．．．．．．．．．．．4.三角形的中线：三角的三条中线相交于一点。

（三角形中线分三角形面积相等的两个三角形）5.三角形的角平分线：在三角形中，一个内角的角平分线与它的对边相交，与之间的线段,叫做三角形的角平分线.三角形三个角的平分线相交于一点．．．．．．．．．．．．．．．三角形的三条中线的交点、三条角平分线的交点在三角形的内部，而锐．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．三角形的三条高的交点在三角形的内部，直角三角形三条高的交战在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6.三角形的稳定性:例1.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.例2.已知：△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求：△ABC的各边的长。

例3.已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长.例4.已知等腰三角形的周长是16cm．（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．例5.已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4,求等腰三角形各边的长。

三角形第一讲与三角形有关的线段1.定义：不在一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

注意：三条线段必须①不在一条直线上，②首尾顺次相接。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC.三角形ABC的顶点C所对的边AB可用c 表示,顶点B所对的边AC可用b表示,顶点A所对的边BC可用a表示.2.三角形三边的不等关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边。

3.三角形的高：从三角形的向它的作垂线，顶点和垂足之间的线段叫做三角形的高,（注意八字形）注意：高与垂线不同，高是线段，垂线是直线。

三角形的三条高相交于一点。

．．．．．．．．．．．．．4.三角形的中线：三角的三条中线相交于一点。

（三角形中线分三角形面积相等的两个三角形）5.三角形的角平分线：在三角形中，一个内角的角平分线与它的对边相交，与之间的线段,叫做三角形的角平分线.三角形三个角的平分线相交于一点．．．．．．．．．．．．．．．三角形的三条中线的交点、三条角平分线的交点在三角形的内部，而锐．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．三角形的三条高的交点在三角形的内部，直角三角形三条高的交战在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6.三角形的稳定性:例1.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.例2.已知：△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求：△ABC 的各边的长。

例3.已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长.例4.已知等腰三角形的周长是16cm．（1）若其中一边长为4cm，求另外两边的长；（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．例5.已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4,求等腰三角形各边的长。

三角形第一讲与三角形有关的线段1.定义：不在一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

注意：三条线段必须①不在一条直线上，②首尾顺次相接。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC.三角形ABC的顶点C所对的边AB可用c 表示,顶点B所对的边AC可用b表示,顶点A所对的边BC可用a表示.2.三角形三边的不等关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边。

3.三角形的高：从三角形的向它的作垂线，顶点和垂足之间的线段叫做三角形的高,（注意八字形）注意：高与垂线不同，高是线段，垂线是直线。

三角形的三条高相交于一点。

．．．．．．．．．．．．．4.三角形的中线：三角的三条中线相交于一点。

（三角形中线分三角形面积相等的两个三角形）5.三角形的角平分线：在三角形中，一个内角的角平分线与它的对边相交，与之间的线段,叫做三角形的角平分线.三角形三个角的平分线相交于一点．．．．．．．．．．．．．．．三角形的三条中线的交点、三条角平分线的交点在三角形的内部，而锐．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．三角形的三条高的交点在三角形的内部，．．．．．．．．．．．．．．．．．．直角三角形三条高的交战在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6.三角形的稳定性:例1.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.例2.已知：△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求：△ABC的各边的长。

例3.已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长.例4.已知等腰三角形的周长是16cm．（1）若其中一边长为4cm，求另外两边的长；（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．例5.已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4,求等腰三角形各边的长。

三角形第一讲与三角形有关的线段1.定义：不在一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

注意：三条线段必须①不在一条直线上，②首尾顺次相接。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC.三角形ABC的顶点C所对的边AB可用c 表示,顶点B所对的边AC可用b表示,顶点A所对的边BC可用a表示.2.三角形三边的不等关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边。

3.三角形的高：从三角形的向它的作垂线，顶点和垂足之间的线段叫做三角形的高,（注意八字形）注意：高与垂线不同，高是线段，垂线是直线。

三角形的三条高相交于一点。

．．．．．．．．．．．．．4.三角形的中线：三角的三条中线相交于一点。

（三角形中线分三角形面积相等的两个三角形）5.三角形的角平分线：在三角形中，一个内角的角平分线与它的对边相交，与之间的线段,叫做三角形的角平分线.三角形三个角的平分线相交于一点．．．．．．．．．．．．．．．三角形的三条中线的交点、三条角平分线的交点在三角形的内部，而锐．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．三角形的三条高的交点在三角形的内部，直角三角形三条高的交战在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6.三角形的稳定性:例1.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.例2.已知：△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求：△ABC 的各边的长。

例3.已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长.例4.已知等腰三角形的周长是16cm．（1）若其中一边长为4cm，求另外两边的长；（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．例5.已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4,求等腰三角形各边的长。

E D CA B M NF CAPQB M第十三讲：轴对称第一部分【能力提高】一、 上图中的图形都是轴对称图形，请你试着画出它们的对称轴．二、如图，△ABC 与△ADE 关于直线MN 对称，BC 与DE 的交点F 在直线MN 上．• ①指出两个三角形中的对称点；②图中还有对称的三角形吗？三、如已知等腰三角形ABC ，AB 边的垂直平分线交AC 于D ，AB=AC=8，BC=6，求△BDC 周长．四、三角形三边垂直平分线的必交于一点.如图，在△ABC 中，边AB 和AC 的垂直平分线MP 、MQ 交于点M ，求证：M 必在线段BC 的垂直平分线上.五、如下图小河边有两个村庄，要在河对岸建一自来水厂向A 村与B 村供水，•要符合条件： （1）若要使厂部到A 、B 的距离相等，则应选在哪儿？（2）若要使厂部到A 村、B 村的水管最省料，应建在什么地方？AHPCQBCAP QD BM第二部分【综合运用】六、（1）在图中所示编号为①、②、③、④的四个三角形中，关于y 轴对称的两个三角形的编号为 ；关于x 轴对称的两个三角形的编号为 ；（2）在图4中，画出与△ABC 关于x 轴对称的△A 1B 1C 1七、如图，AM 平分∠PAQ ，B 为AM 上任一点，BC ⊥AP 于点C ，BD ⊥AQ 于点Q ，求证：AB 垂直平分线段CD.八、如图，△ABC 中，∠BAC 的平分线交边BC 的垂直平分线PQ 于点P.（1）求证：AB-AC=2BH ；（2）求AB ACAH的值.AFECB第 13 讲 作 业一．选择题1．国旗是一个国家的象征，观察下面的国旗，是轴对称图形的是( ). (A)加拿大、哥斯达黎加、乌拉圭 (B)加拿大、瑞典、澳大利亚 (C)加拿大、瑞典、瑞士 (D)乌拉圭、瑞典、瑞士加拿大 哥斯达黎加 澳大利亚 乌拉圭 瑞典 瑞士2．对称现象无处不在，请你观察下面的四个图形，它们体现了中华民族的传统文化，其中，可以看作是轴对称图形的有( ). (A)1个 (B)2个 (C)3个 (D)4个 3．下列图形中，不是轴对称图形的是( ).(A)一条线段 (B)两条相交的直线(C)有公共端点的两条相等的线段 (D)有公共端点的两条不相等的线段 4．下列图形中，不是轴对称图形的是( ).(A)平行四边形 (B)长方形 (C)正方形 (D)圆 5．下列说法错误的是 （ ）(A)关于某条直线对称的两个三角形一定全等 (B)轴对称图形至少有一条对称轴 (C)全等三角形一定能关于某条直线对称 (D)角是关于它的平分线对称的图形 6. 下列命题中，不正确的是( ). (A)关于直线对称的两个三角形一定全等.(B)两个大小一样的圆形纸片随意平放在水平桌面上构成轴对称图形. (C)若两图形关于直线对称，则对称轴是对应点所连线段的垂直平分线. (D)等腰三角形一边上的高、中线及这边对角平分线重台. 7．图中是一个经过改造的台球桌面的示意图，图中四个角上的阴影 部分分别表示四个入球孔.如果一个球按图中所示的方向被击出（球 可以经过多次反射），那么该球最后将落入的球袋是( ). (A)1 号袋 (B)2 号袋 (A)3 号袋 (D)4 号袋 8.在平面直角坐标系中，点(3，4)关于x 轴对称点的坐标是( ).(A)(4，3) (B)(3，-4) (C)(-3， 4) (D)(-3，-4)9．如图,六边形ABCDEF 是轴对称图形,CF 所在的直线是它的对称轴，若∠AFC+∠BCF=150°，则∠AFE+∠BCD 的大小是( ). (A)150° (B)300°(C)210°(D)330°41E D C B A 1E 2F D C B A10．下列图形中，△A ’B ’C ’与△ABC 关于直线MN 成轴对称的是( ).11．在平面直角坐标系中，将点A （1，2）的横坐标乘以-1，纵坐标不变，得到点A '，则点A 与点A '的关系是( ).(A)关于x 轴对称 (B)关于y 轴对称(C)关于原点对称 (D)将点A 向x 轴负方向平移一个单位得点A ' 12．如图，Rt △ABC 中，∠B=90°，AB=3，BC=4，AC=5，将△ABC 折叠，使点C 与A 重合，得折痕DE ，则△ABE 的周长等于( ).(A)9cm (B)8cm (C)7cm (D)1213．如图，是用平行四边形纸条沿对边AB 、CD 的中点E 、F 所在直线折成的V 字形图案，已知图中∠1=68°，则∠2的度数为( ).(A)56° (B)44° (C)68° (D)52°14．如图，是一个风筝的图案，它是轴对称图形，量得∠AEB=140°，AC ⊥AE ，∠C=60°，则∠CFD 的度数为( ).(A)140° (B)150° (C)160° (D)170° 15．如图，把矩形ABCD 沿EF 对折，若∠1=50°，则∠AEF 等于( ).(A)115°(B)130°(C)120°(D)65°16如图，将矩形ABCD 沿AE 折叠，若∠BAD ′=20°，则∠C ED′等于( ).(A)40°(B)50° (C)60°(D)70°17．图，将五边形ABCDE 按如图方式折叠，折痕为AF ，点E 、D 分别落在点E '、D '.已知∠AFC=76°，则∠CFD '等于（ ）.(A)31° (B)28° (C)24° (D)22°FE D C BA F E'D'EDC BACD E BA18．把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换．．．．．．．在自然界和日常生活中，大量地存在这种图形变换（如图1）．结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换．．．．．．过程中，两个对应三角形（如图2）的对应点所具有的性质是( ). (A)对应点连线与对称轴垂直 (B)对应点连线被对称轴平分 (C)对应点连线被对称轴垂直平分 (D)对应点连线互相平行二．填空题19.把一个图形沿某一条直线_________，如果它能够与另一个图形________，•那么就说这两个图形关于这条直线____________．20. 角的对称轴是 .线段是轴对称图形，有 条对称轴，对称轴是 .21.如果一个图形沿某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做__________． 22.如图，在△ABC 中，AC ＝8cm ，ED 垂直平分AB ，若△EBC 的 周长是14cm ，那么BC 的长度为 。

三角形第一讲与三角形有关的线段1.定义：不在一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

注意：三条线段必须①不在一条直线上，②首尾顺次相接。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC.三角形ABC的顶点C所对的边AB可用c 表示,顶点B所对的边AC可用b表示,顶点A所对的边BC可用a表示.2.三角形三边的不等关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边。

3.三角形的高：从三角形的向它的作垂线，顶点和垂足之间的线段叫做三角形的高,（注意八字形）注意：高与垂线不同，高是线段，垂线是直线。

三角形的三条高相交于一点。

．．．．．．．．．．．．．4.三角形的中线：三角的三条中线相交于一点。

（三角形中线分三角形面积相等的两个三角形）5.三角形的角平分线：在三角形中，一个内角的角平分线与它的对边相交，与之间的线段,叫做三角形的角平分线.三角形三个角的平分线相交于一点．．．．．．．．．．．．．．．三角形的三条中线的交点、三条角平分线的交点在三角形的内部，而锐．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．三角形的三条高的交点在三角形的内部，直角三角形三条高的交战在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6.三角形的稳定性:例1.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.例2.已知：△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求：△ABC 的各边的长。

例3.已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长.例4.已知等腰三角形的周长是16cm．（1）若其中一边长为4cm，求另外两边的长；（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．例5.已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4,求等腰三角形各边的长。

三角形第一讲与三角形有关的线段1.定义：不在一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

注意：三条线段必须①不在一条直线上，②首尾顺次相接。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC.三角形ABC的顶点C所对的边AB可用c 表示,顶点B所对的边AC可用b表示,顶点A所对的边BC可用a表示.2.三角形三边的不等关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边。

3.三角形的高：从三角形的向它的作垂线，顶点和垂足之间的线段叫做三角形的高,（注意八字形）注意：高与垂线不同，高是线段，垂线是直线。

三角形的三条高相交于一点。

．．．．．．．．．．．．．4.三角形的中线：三角的三条中线相交于一点。

（三角形中线分三角形面积相等的两个三角形）5.三角形的角平分线：在三角形中，一个内角的角平分线与它的对边相交，与之间的线段,叫做三角形的角平分线.三角形三个角的平分线相交于一点．．．．．．．．．．．．．．．三角形的三条中线的交点、三条角平分线的交点在三角形的内部，而锐．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．三角形的三条高的交点在三角形的内部，直角三角形三条高的交战在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6.三角形的稳定性:例1.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.例2.已知：△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求：△ABC 的各边的长。

例3.已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长.例4.已知等腰三角形的周长是16cm．（1）若其中一边长为4cm，求另外两边的长；（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．例5.已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4,求等腰三角形各边的长。

三角形第一讲与三角形有关的线段1.定义：不在一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

注意：三条线段必须①不在一条直线上，②首尾顺次相接。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC.三角形ABC的顶点C所对的边AB可用c 表示,顶点B所对的边AC可用b表示,顶点A所对的边BC可用a表示.2.三角形三边的不等关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边。

3.三角形的高：从三角形的向它的作垂线，顶点和垂足之间的线段叫做三角形的高,（注意八字形）注意：高与垂线不同，高是线段，垂线是直线。

三角形的三条高相交于一点。

．．．．．．．．．．．．．4.三角形的中线：三角的三条中线相交于一点。

（三角形中线分三角形面积相等的两个三角形）5.三角形的角平分线：在三角形中，一个内角的角平分线与它的对边相交，与之间的线段,叫做三角形的角平分线.三角形三个角的平分线相交于一点．．．．．．．．．．．．．．．三角形的三条中线的交点、三条角平分线的交点在三角形的内部，而锐．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．三角形的三条高的交点在三角形的内部，直角三角形三条高的交战在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6.三角形的稳定性:例1.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.例2.已知：△ABC的周长为48cm，最大边与最小边之差为14cm，另一边与最小边之和为25cm，求：△ABC 的各边的长。

例3.已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长.例4.已知等腰三角形的周长是16cm．（1）若其中一边长为4cm，求另外两边的长；（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．例5.已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4,求等腰三角形各边的长。