平行四边形、三角形、梯形 面积推导过程(整理)
- 格式:docx
- 大小:63.63 KB
- 文档页数:2

周长:圆、椭圆或其他闭合的曲线的周界长度。
面积:物体的表面—平面图形的大小,叫做它们的面积。
圆面积推导过程:1、把圆16等份分割后拼插成近似的平行四边形,平行四边形的底相当于圆周长的四分之一(C/4=πr/2),高等于圆半径的2倍(2r),所以S=πr/2·2r=πr22、把圆16等份分割后可拼插成近似的等腰三角形。
三角形的底相当于圆周长的1/4,高相当于圆半径的4倍,所以S=1/2·2πr/4r=πr23、把圆分割后,可拼成近似的等腰梯形。
梯形上底与下底的和就是圆周长的一半,高等于圆半径的2倍,所以S=1/2·πr·2r=πr2。
4、小结:无论我们把圆拼成什么样的近似图形,都能推导出圆的面积公式S=πr2,验证了原来猜想的正确。
说明在求圆的面积时,都要知道半径。
三角形面积推导过程:1:把一个等腰三角形对折,然后从中间剪开拼成了一个长方形,这个长方形的底是三角形的底的一半,高是三角形的高,因为长方形的面积是长×宽,长方形的面积等于三角形的面积,所以三角形的面积是底×高÷2。
2:把一个直角三角形的上面对折下来,然后剪开,把它补在一边,拼成了一个长方形。
这个长方形的长是三角形的底,高是三角形高的一半,所以也能推出三角形的面积是底×高÷2。
3:把一个三角形沿着两边的重点对折,然后又把底边的重点这样对折,折成了一个长方形,这个长方形的底是三角形底的一半,宽是三角形高的一半,再乘以2,也可以推出三角形的面积是底×高÷24:把一个长方形沿对角线折叠,因为长方形的面积是长×宽,长方形是两个三角形拼成的,所以,三角形的面积是底×高÷2梯形面积推导过程:1、用两个完全一样的梯形通过旋转拼成了一个长方形,观察后发现:梯形的上下底之和相当于长方形的长、梯形的高相当于长方形的宽、梯形的面积=长方形的面积÷2(或梯形的面积等于长方形的面积的一半),根据拼成图形的面积公式是:长方形的面积=长×宽,所以:梯形的面积=(上底+下底)×高÷22、梯形的上下底之和相当于平行四边形的底,梯形的高相当于平行四边形的高,梯形的面积相当于平行四边形面积的一半。

平面图形的推导过程及公式Prepared on 22 November 2020周长:圆、椭圆或其他闭合的曲线的周界长度。
面积:物体的表面—平面图形的大小,叫做它们的面积。
圆面积推导过程:1、把圆16等份分割后拼插成近似的平行四边形,平行四边形的底相当于圆周长的四分之一(C/4=πr/2),高等于圆半径的2倍(2r),所以S=πr/2·2r=πr22、把圆16等份分割后可拼插成近似的等腰三角形。
三角形的底相当于圆周长的1/4,高相当于圆半径的4倍,所以S=1/2·2πr/4r=πr23、把圆分割后,可拼成近似的等腰梯形。
梯形上底与下底的和就是圆周长的一半,高等于圆半径的2倍,所以S=1/2·πr·2r=πr2 。
4、小结:无论我们把圆拼成什么样的近似图形,都能推导出圆的面积公式S=πr2,验证了原来猜想的正确。
说明在求圆的面积时,都要知道半径。
三角形面积推导过程:1:把一个等腰三角形对折,然后从中间剪开拼成了一个长方形,这个长方形的底是三角形的底的一半,高是三角形的高,因为长方形的面积是长×宽,长方形的面积等于三角形的面积,所以三角形的面积是底×高÷2。
2:把一个直角三角形的上面对折下来,然后剪开,把它补在一边,拼成了一个长方形。
这个长方形的长是三角形的底,高是三角形高的一半,所以也能推出三角形的面积是底×高÷2。
3:把一个三角形沿着两边的重点对折,然后又把底边的重点这样对折,折成了一个长方形,这个长方形的底是三角形底的一半,宽是三角形高的一半,再乘以2,也可以推出三角形的面积是底×高÷24:把一个长方形沿对角线折叠,因为长方形的面积是长×宽,长方形是两个三角形拼成的,所以,三角形的面积是底×高÷2梯形面积推导过程:1、用两个完全一样的梯形通过旋转拼成了一个长方形,观察后发现:梯形的上下底之和相当于长方形的长、梯形的高相当于长方形的宽、梯形的面积=长方形的面积÷2(或梯形的面积等于长方形的面积的一半),根据拼成图形的面积公式是:长方形的面积=长×宽,所以:梯形的面积=(上底+下底)×高÷22、梯形的上下底之和相当于平行四边形的底,梯形的高相当于平行四边形的高,梯形的面积相当于平行四边形面积的一半。

平行四边形三角形梯形面积推导过程一、平行四边形的面积推导过程:(1)定义:平行四边形是具有两组平行边的四边形。
(2)面积公式:平行四边形的面积等于底边长度乘以高度。
设平行四边形的底边长为b,高度为h。
根据定义可知,平行四边形的对边平行,所以可以将其视为横向的矩形和纵向的矩形组合而成。
其中,横向矩形的底边长度为b,高度为h,面积为bh;纵向矩形的底边长度为h,高度为b,面积为hb。
因此,平行四边形的面积等于这两个矩形的面积之和,即S=bh+hb=2bh。
所以,平行四边形的面积为2bh。
二、三角形的面积推导过程:(1)定义:三角形是由三条边和三个夹角组成的几何形状。
(2)面积公式:三角形的面积等于底边长度乘以高度再除以2设三角形的底边长为b,高度为h。
可以将三角形划分为底边b和高度h所形成的矩形和一个三角形。
其中,矩形的面积为bh,三角形的面积为矩形面积的一半,即bh/2所以,三角形的面积为bh/2三、梯形的面积推导过程:(1)定义:梯形是具有两条平行边的四边形。
(2)面积公式:梯形的面积等于上底和下底的和乘以高度再除以2设梯形的上底长为a,下底长为b,高度为h。
可以将梯形看作一个上底为a,下底为b,高度为h的平行四边形,再去掉一个上底为a,下底为b,高度为h/2的三角形。
根据平行四边形的面积公式可得,平行四边形的面积为(a+b)h。
所以,梯形的面积为(a+b)h/2综上所述,平行四边形的面积为2bh,三角形的面积为bh/2,梯形的面积为(a+b)h/2、这些面积公式的推导过程是基于几何形状的特性和定义进行的。
通过对这些公式的应用,我们可以方便地计算出平行四边形、三角形和梯形的面积。


平行四边形面积推导过程思路嘿,咱今儿个就来唠唠平行四边形面积推导过程思路这档子事儿!你想想看啊,平行四边形那模样,就像是被人斜着拉了一下的长方形。
那咱咋知道它的面积咋算呢?这就得动点小脑筋啦!咱可以拿个平行四边形出来,就像手里捧着个宝贝似的。
然后呢,咱沿着一条高给它剪一刀,嘿,这一剪可就有意思了,就变成一个三角形和一个梯形啦!接着呢,咱把这个三角形挪一挪,诶,你猜怎么着,它和那个梯形就能拼成一个长方形啦!这就好比是变魔术一样,一下子就把平行四边形给变成咱熟悉的长方形啦!那长方形的面积咱会算呀,长乘以宽嘛!那这个平行四边形的面积不也就出来啦?原来的底就是现在长方形的长,原来的高就是现在长方形的宽呀!你说这巧妙不巧妙?这不就跟咱生活中好多事儿一样嘛,看着挺复杂,其实找对了方法,一下子就简单了。
就好比你要解开一团乱麻,找到了线头,轻轻一拉,就顺啦!咱再换个角度想想,要是没有这个推导过程,那算平行四边形面积得多难呀!咱得绞尽脑汁想各种办法,说不定还会算错呢!现在有了这个思路,就像是有了一把钥匙,轻轻一转,门就开啦!你说这数学是不是很神奇呀?一个小小的平行四边形面积推导,就能让咱看到那么多的智慧和巧妙。
这就跟咱走路一样,找到了正确的路,那走起来就顺风顺水啦!咱再想想,要是以后遇到其他形状的面积问题,是不是也可以用类似的方法去推导呀?说不定就能发现新的惊喜呢!所以说呀,这平行四边形面积推导过程思路可太重要啦!它不仅教会了我们怎么算面积,还让我们看到了数学的魅力和乐趣。
以后咱再看到平行四边形,就不会发怵啦,心里就有底啦,知道该怎么去算它的面积啦!总之呢,这平行四边形面积推导过程思路就像是一盏明灯,照亮了我们学习数学的路,让我们能在数学的海洋里畅游,发现更多的精彩和奥秘!你说是不是呀?。

面积推导过程和公式长方形正方形平行四边形三角形梯形圆Calculating the area of different geometric shapes is a fundamental concept in mathematics. Understanding how to derive and apply the formula for the area of a shape is essential for problem-solving and real-world applications. Whether it's finding the area of a rectangle, square, parallelogram, triangle, trapezoid, or circle, each shape hasits own unique formula that can be derived from basic principles of geometry.计算不同几何形状的面积是数学中的一个基本概念。
理解如何推导和应用形状面积的公式对于问题解决和现实应用至关重要。
不管是找到长方形、正方形、平行四边形、三角形、梯形还是圆的面积,每种形状都有其独特的公式,可以从几何的基本原理推导出来。
Let's start with the area of a rectangle. The formula for the area of a rectangle is simply the product of its length and width. This makes intuitive sense, as the area of a rectangle is essentially a two-dimensional representation of the space enclosed by its four sides.By multiplying the length and width, we effectively calculate the total amount of space within the rectangle.让我们从长方形的面积开始。
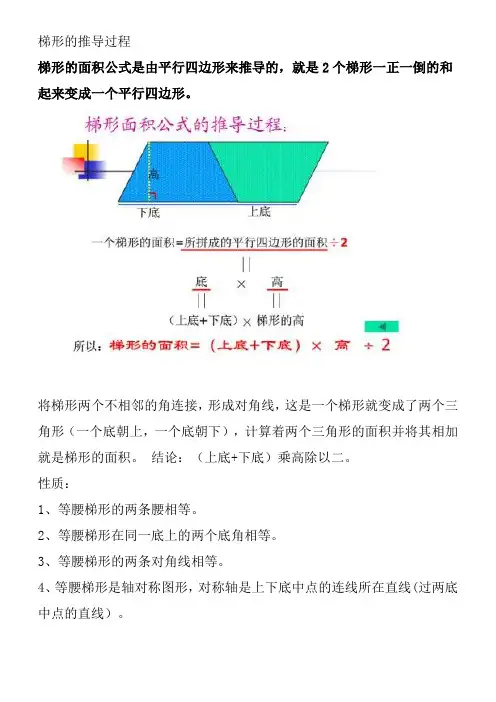
梯形的推导过程
梯形的面积公式是由平行四边形来推导的,就是2个梯形一正一倒的和起来变成一个平行四边形。
将梯形两个不相邻的角连接,形成对角线,这是一个梯形就变成了两个三角形(一个底朝上,一个底朝下),计算着两个三角形的面积并将其相加就是梯形的面积。
结论:(上底+下底)乘高除以二。
性质:
1、等腰梯形的两条腰相等。
2、等腰梯形在同一底上的两个底角相等。
3、等腰梯形的两条对角线相等。
4、等腰梯形是轴对称图形,对称轴是上下底中点的连线所在直线(过两底中点的直线)。

梯形公式推导过程
推导一:甲、乙两个梯形全等,且上底为a,下底为b,高为h。
将这两个梯形拼接成一个平行四边形,则平行四边形的一条底边长为a+b,此底边上的高与梯形的高h相等,那么一个梯形的面积是平行四边形面积的一半。
(参见图一)
梯形的面积=(a+b)h÷2=1/2(a+b)h 。
推导二:一个梯形上底为a,下底为b,高为h。
在梯形内连接一组对角的顶点作一虚线,将三角形沿中点旋转,拼成一个大三角形。
(参见图二)则有:
梯形的面积=(b+a)h÷2=1/2(a+b)h 。
推导三:一个梯形上底为a,下底为b,高为h。
在梯形内连接顶点到一腰中点作一虚线,将梯形分为两个等高不同底的三角形。
(参见图三)则有:
第一个三角形的面积=1/2ah。
第二个三角形的面积=1/2bh。
梯形的面积=1/2ah+1/2bh=1/2(a+b)h 。
推导四:一个梯形上底为a,下底为b,高为h。
在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。
(参见图四)则有:
平行四边形的面积=ah 。
三角形的面积=(b-a)h÷2=1/2bh-1/2ah 。
梯形的面积= ah+1/2bh-1/2ah=1/2ah+1/2bh=1/2(a+b)h。

梯形面积公式推导的多样方法梯形是一个四边形,其中两边是平行的,且其他两边不平行。
梯形的面积可以使用多种方法来推导。
方法一:使用三角形面积公式推导梯形可以被分割为两个三角形和一个矩形。
我们可以使用三角形的面积公式来推导梯形的面积。
假设梯形的上底为a,下底为b,高为h。
我们可以将梯形分割成两个三角形:一个底边为a,高为h的三角形和一个底边为b,高为h的三角形。
我们还可以将梯形分割成一个底边为b-a,高为h的矩形和一个底边为b,高为h的三角形。
根据三角形的面积公式,第一个三角形的面积为1/2*a*h,第二个三角形的面积为1/2*b*h。
因此,两个三角形的总面积为1/2*a*h+1/2*b*h,即(h/2)*(a+b)。
根据矩形的面积公式,矩形的面积为(b-a)*h。
将两个三角形的面积和矩形的面积相加,得到梯形的面积公式为:(h/2)*(a+b)+(b-a)*h=(a+b)*h。
方法二:使用高和中线推导梯形的面积也可以使用梯形的高和中线来推导。
假设梯形的上底为a,下底为b,高为h,两条中线分别为m₁和m₂。
我们可以将梯形分割成两个三角形和一个平行四边形。
平行四边形的高为h,底边为m₂-m₁。
根据三角形的面积公式,由高h和底边m₂-m₁组成的三角形的面积为1/2*(m₂-m₁)*h。
根据平行四边形的面积公式,平行四边形的面积为底边乘以高,即(m₂-m₁)*h。
将两个三角形的面积和平行四边形的面积相加,得到梯形的面积公式为:1/2*(m₂-m₁)*h+(m₂-m₁)*h=(m₂-m₁)*h*(1/2+1)=(m₂-m₁)*h*3/2因此,梯形的面积可以表示为梯形的高h乘以梯形的两条中线之差m₂-m₁再乘以3/2方法三:使用角度和边长推导梯形的面积也可以使用梯形的角度和边长来推导。
假设梯形的上底为a,下底为b,高为h,两条斜边分别为c₁和c₂,两个角分别为θ₁和θ₂。
我们可以将梯形视为一个三角形和一个梯形组成。

平行四边形面积和三角形面积的计算(教师版)学生/课程年级学科授课教师日期时段核心内容平行四边形面积、三角形面积。
课型教学目标1、理解平行四边形和三角形面积公式的推导2、明确等底等高的三角形与平行四边形面积的关系3、能熟练地运用面积公式计算平行四边形和三角形的面积重、难点平行四边形、三角形面积公式的推导和应用;求组合图形的面积。
知识导图导学一:平行四边形知识点讲解1:平行四边形面积公式的推导和应用利用割补法,可将平行四边形转化成已学过的长方形,再根据长方形的面积公式推导出平行四边形的面积公式。
从上图可以看出,平行四边形的底、高分别等于长方形的长、宽,平行四边形的面积等于长方形的面积。
所以:平行四边形面积用字母表示:S = a × h知识点讲解2:等底等高的两个四边形面积关系。
下面每个图中的两个四边形的面积有什么关系?等底等高的两个平行四边形面积。
等底等高的平行四边形和正方形面积。
等底等高的平行四边形和长方形面积。
规律:等底等高的两个四边形面积______________ 。
知识点讲解3:把一个长方形拉成一个平行四边形,它们的面积和周长会有变化吗?3:把一个长方形拉成一个平行四边形,它们的面积和周长会有变化吗?变化规律:长方形的面积平行四边形的面积;长方形的周长平行四边形的周长。
例题1.[平行四边形的面积] [难度:★★★ ] 如下图,这个平行四边形的面积是()平方厘米。
【参考答案】面谈一刻答案:1.942 2.8厘米本题答案:1082.[平行四边形的面积] [难度:★★★ ] 判断:一个平行四边形的的底和高都扩大2倍,则它的面积也会扩大2倍。
()【参考答案】错【题目解析】底×2,面积×2,高×2,面积×2,最后×2×2=×4,扩大4倍3.[平行四边形的面积] [难度:★★★ ] 判断:将一个平行四边形沿高剪开,拼成长方形后,它的面积变大了。

梯形面积的推导过程
推导一:甲、乙两个梯形全等,且上底为a,下底为b,高为h。
将这两个梯形拼接成一个平行四边形,则平行四边形的一条底边长为a+b,此底边上的高与梯形的高h相等,那么一个梯形的面积是平行四边形面积的一半。
(参见图一)梯形的面积=(a+b)h÷2=1/2(a+b)h 。
推导二:一个梯形上底为a,下底为b,高为h。
在梯形内连接一组对角的顶点作一虚线,将三角形沿中点旋转,拼成一个大三角形。
(参见图二)则有:
梯形的面积=(b+a)h÷2=1/2(a+b)h 。
推导三:一个梯形上底为a,下底为b,高为h。
在梯形内连接顶点到一腰中点作一虚线,将梯形分为两个等高不同底的三角形。
(参见图三)则有:
第一个三角形的面积=1/2ah。
第二个三角形的面积=1/2bh。
梯形的面积=1/2ah+1/2bh=1/2(a+b)h 。
推导四:一个梯形上底为a,下底为b,高为h。
在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。
(参见图四)则有:
平行四边形的面积=ah 。
三角形的面积=(b-a)h÷2=1/2bh-1/2ah 。
梯形的面积= ah+1/2bh-1/2ah=1/2ah+1/2bh=1/2(a+b)h。
平面图形的推导过程及公式Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】周长:圆、椭圆或其他闭合的曲线的周界长度。
面积:物体的表面—平面图形的大小,叫做它们的面积。
圆面积推导过程:1、把圆16等份分割后拼插成近似的平行四边形,平行四边形的底相当于圆周长的四分之一(C/4=πr/2),高等于圆半径的2倍(2r),所以S=πr/2·2r=πr22、把圆16等份分割后可拼插成近似的等腰三角形。
三角形的底相当于圆周长的1/4,高相当于圆半径的4倍,所以S=1/2·2πr/4r=πr23、把圆分割后,可拼成近似的等腰梯形。
梯形上底与下底的和就是圆周长的一半,高等于圆半径的2倍,所以S=1/2·πr·2r=πr2 。
4、小结:无论我们把圆拼成什么样的近似图形,都能推导出圆的面积公式S=πr2,验证了原来猜想的正确。
说明在求圆的面积时,都要知道半径。
三角形面积推导过程:1:把一个等腰三角形对折,然后从中间剪开拼成了一个长方形,这个长方形的底是三角形的底的一半,高是三角形的高,因为长方形的面积是长×宽,长方形的面积等于三角形的面积,所以三角形的面积是底×高÷2。
2:把一个直角三角形的上面对折下来,然后剪开,把它补在一边,拼成了一个长方形。
这个长方形的长是三角形的底,高是三角形高的一半,所以也能推出三角形的面积是底×高÷2。
3:把一个三角形沿着两边的重点对折,然后又把底边的重点这样对折,折成了一个长方形,这个长方形的底是三角形底的一半,宽是三角形高的一半,再乘以2,也可以推出三角形的面积是底×高÷24:把一个长方形沿对角线折叠,因为长方形的面积是长×宽,长方形是两个三角形拼成的,所以,三角形的面积是底×高÷2梯形面积推导过程:1、用两个完全一样的梯形通过旋转拼成了一个长方形,观察后发现:梯形的上下底之和相当于长方形的长、梯形的高相当于长方形的宽、梯形的面积=长方形的面积÷2(或梯形的面积等于长方形的面积的一半),根据拼成图形的面积公式是:长方形的面积=长×宽,所以:梯形的面积=(上底+下底)×高÷22、梯形的上下底之和相当于平行四边形的底,梯形的高相当于平行四边形的高,梯形的面积相当于平行四边形面积的一半。
1、平行四边形面积推导过程:
方法一:
平行四边形面积计算公式的推导过程:
把平行四边形沿高剪开,拼成一个长方形,拼成长方形的长等于原平行四边形的底,拼成长方形的宽等于原平行四边形的高,因为长方形的面积=长×宽,所以平行四边形的面积=底×高公式S=ah。
方法二:
将一个平行四边形沿高剪下,拼到另一边,则拼成一个长方形。
h
a
平行四边形的面积等于长方形的面积。
平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。
因为长方形的面积= 长х宽
平行四边形的面积=底х高
所以,平行四边形的面积公式则为底乘高,S = a h
2、三角形面积推导过程
两个一模一样的三角形,可以拼成一个平行四边行形。
H
两个完全一样的三角形能拼成一个平行四边形,三角形的面积是拼成平行四边形面积的一半,三角形的高就就是这个平行四边形的高,三角形的底也是这个平行四边形的底。
平行四边形的面积=底边×高,所以三角形的面积=(同底等高的)平行四边形的面积÷2=底×高÷2 ,公式S= a×h÷2
3、梯形面积推导过程
两个完全一样的梯形可以拼成一个平行四边形,原梯形的面积是拼成平行四边形面积的一半,拼成平行四边形的底是原梯形的上底与下底的和,拼成平行四边形的高是原梯形的高,所以梯形的面积=(上底+下底)×高÷2 公式S=(a+b)×h÷2;
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
精品文档
. 梯形面积公式的推导方法
图一 图二
图三 图四
梯形的面积公式可用以下四种方法进行推导。
推导一:甲、乙两个梯形全等,且上底为a ,下底为b ,高为h 。
将这两个梯形拼接成一个平行四边形,则平行四边形的一条底边长为a+b ,此底边上的高与梯形的高h 相等,那么一个梯形的面积是平行四边形面积的一半。
(参见图一)
梯形的面积=(a+b )h ÷2=1/2(a+b )h
推导二:一个梯形上底为a ,下底为b ,高为h 。
在梯形内连接一组对角的顶点作一虚线,将三角形沿中点旋转,拼成一个大三角形。
(参见图二)则有:
梯形的面积=(b+a )h ÷2=1/2(a+b )h
推导三:一个梯形上底为a ,下底为b ,高为h 。
在梯形内连接顶点到一腰中点作一虚线,将梯形分为两个等高不同底的三角形。
(参见图三)则有:
第一个三角形的面积=1/2ah
第二个三角形的面积=1/2bh
梯形的面积=1/2ah+1/2bh=1/2(a+b )h
推导四:一个梯形上底为a ,下底为b ,高为h 。
在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。
(参见图四)则有:
平行四边形的面积=ah
三角形的面积=(b -a )h ÷2=1/2bh -1/2ah
梯形的面积= ah+1/2bh -1/2ah=1/2ah+1/2bh=1/2(a+b )h。
梯形面积公式四种推导方法方法一、将两个完全一样的梯形拼成一个平行四边形。
(如图)拼成之后的平行四边形的底等于梯形的上底和下底的和(a+b),平行四边形的高等于三角形的高h,而平行四边形的面积等于三角形面积的两倍。
因为平行四边形的面积=底×高=(梯形的上底+下底)×梯形的高所以梯形的面积=(梯形的上底+下底)×梯形的高÷2用字母表示:S=(a+b)h÷2方法二、连接AC或BD,梯形被分成了两个三角形。
(如图)三角形ABC的底为梯形的上底a,高就是梯形的高h;三角形ADC的底为梯形的下底b,高同样是梯形的高h。
梯形的面积=三角形ABC的面积+三角形ADC的面积即: S=ah÷2+bh÷2=(ah+bh)÷2=(a+b)h÷2方法三、如图,连接A点和腰BC的中点并延长,交DC的延长线于F点。
由图可知,阴影部分是完全相同的两个三角形,将上面的阴影部分移到下面,梯形变成了一个大三角形ADF。
梯形的面积就等于大三角形ADF的面积。
而大三角形的底为梯形的上底与下底的和(a+b),大三角形的高就是梯形的高h。
直接利用三角形的面积公式即可得出:S=(a+b)h÷2方法四、将梯形对折,使得上下两条底互相重合,再将左右两边的两个小三角形对折,使梯形变成一个小的长方形。
(如图)观察发现,这个长方形的面积等于梯形面积的一半。
长方形的长等于梯形的上底与下底和的一半(a+b)÷2,长方形的宽等于梯形的高的一半(h÷2)。
梯形的面积=长方形的面积×2=长×宽×2S=(a+b)÷2×h÷2×2=(a+b)÷2×h=(a+b)h÷2。
1、平行四边形面积推导过程:
方法一:
平行四边形面积计算公式的推导过程:
把平行四边形沿高剪开,拼成一个长方形,拼成长方形的长等于原平行四边形的底,拼成长方形的宽等于原平行四边形的高,因为长方形的面积=长×宽,所以平行四边形的面积=底×高公式S=ah。
方法二:
将一个平行四边形沿高剪下,拼到另一边,则拼成一个长方形。
h
a
平行四边形的面积等于长方形的面积。
平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。
因为长方形的面积= 长х宽
平行四边形的面积=底х高
所以,平行四边形的面积公式则为底乘高,S = a h
2、三角形面积推导过程
两个一模一样的三角形,可以拼成一个平行四边行形。
H
两个完全一样的三角形能拼成一个平行四边形,三角形的面积是拼成平行四边形面积的一半,三角形的高就就是这个平行四边形的高,三角形的底也是这个平行四边形的底。
平行四边形的面积=底边×高,所以三角形的面积=(同底等高的)平行四边形的面积÷2=底×高÷2 ,公式S= a×h÷2
3、梯形面积推导过程
两个完全一样的梯形可以拼成一个平行四边形,原梯形的面积是拼成平行四边形面积的一半,拼成平行四边形的底是原梯形的上底与下底的和,拼成平行四边形的高是原梯形的高,所以梯形的面积=(上底+下底)×高÷2 公式S=(a+b)×h÷2;。