第三章 应力和应变
- 格式:ppt
- 大小:525.00 KB
- 文档页数:33








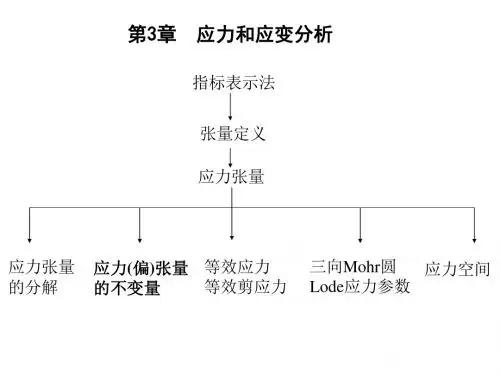

应力与应变的关系
应力与应变是相互关联的概念,有着密切的关系。
下文将对应力与应变的关系
作详细的解释。
首先,需要了解应力和应变的概念,应力是一种外力对材料的作用,包括张力,剪力,扭转力和摩擦。
应变本质上是材料力学特性的变化,是以体积为例子的变形,受应力的强大影响而形成的。
其次,应力和应变的关系本质上是一种“折中”的关系,材料对某种外力的反
应强度不定;受应力越大,应变就会越大,物体越有可能变形;受应力越小,应变就会越小,这就说明应力和应变之间呈现出正比的关系。
正是基于这种关系,受应力的大小可以通过测量材料的应变来表示,这是测定应力的一种重要方式。
最后,由于应力与应变之间的密切关系,对其进行计算模拟可以有效预测在应
力作用下材料的表现,科学上精确的计算模型可以模拟出完整的应力、应变关系并用于进行预测。
总之,应力与应变之间的关系是相互关联的,相互影响的关系。
它具有很强的
可预测性、可算法化的特点,可以更好地解释材料行为,并且为预测带来很大的方便。
第三章杆件横截面上的应力应变分析利用截面法可以确定静定问题中的杆件横截面上的内力分量,但内力分量只是横截面上连续分布内力系的简化结果,仅根据内力并不能判断杆件是否有足够的强度。
如用同一种材料制成粗细不同的两根杆,在相同的拉力作用下,两杆的轴力是相同的,当拉力增大时,细杆必定先被拉断。
这说明拉杆的强度不仅与轴力大小有关,还与横截面面积有关,因此还必须引入内力集度的概,即应力的概念。
本章在此基础上分别讨论了杆件在拉压、扭转和弯曲三种基本变形和组合变形下横截面上应力的分布规律,导出了应力计算公式,为后面对杆件进行强度计算打下了基础。
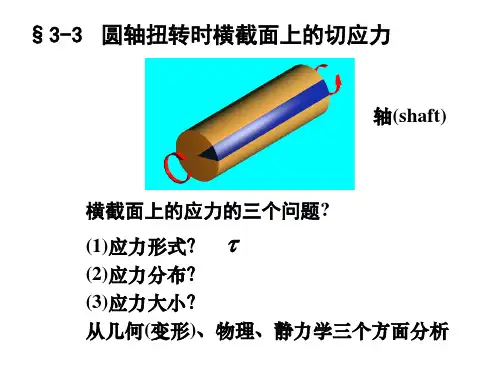
第一节应力、应变及其相互关系一、正应力、剪应力观察图3-1a所示受力杆件,在截面上围绕K点取微小面积,其上作用有微内力,于是在上内力的平均集度为:(3-1)亦称为面积上的平均应力。
一般来说截面上的内力并不均匀分布,因此平均应力随所取ΔA的不同而变化。
当ΔA趋向于零时,的大小方向都将逐渐趋于某一极限。
(3-2)式中,p称为K点的应力,它反映内力系在K点的强弱程度。
p是一个矢量,一般说既不与截面垂直,也不与截面相切。
通常将其分解为垂直于截面的应力分量和相切于截面的应力分量(图3-1b)。
称为正应力,称为切应力。
在国际单位制中,应力的单位是牛顿/米2(N/M2),称为帕斯卡,简称帕(Pa)。
由于这个单位太小,通常使用兆帕(MPa),1MPa = 106Pa。
二、正应变、切应变杆件在外力作用下,其尺寸或几何形状将发生变化。
若围绕受力弹性体中任意点截取一个微小正六面体(当六面体的边长趋于无限小时称为单元体),六面体的棱边边长分别为Δx 、Δy 、Δz (图3-2 )。
把该六面体投影到xy平面(图3-2b)。
变形后,六面体的边长和棱边夹角都将发生变化(图3-2c)。
变形前长为Δx的线段MN,变形后长度为Δx+Δs。
相对变形(3-3)表示线段MN单位长度的平均伸长或缩短,称为平均应变。
当Δx趋向于零,即点N趋向于M点时,其极限为(3-4)式中,ε称为M点沿x方向的线应变或正应变,ε为无量纲量。
应力与应变概念解释在物理学和材料科学领域中,应力(stress)和应变(strain)是两个重要的概念。
应力描述的是物体内部的力状态,而应变描述的是物体对于应力的响应。
理解应力和应变的关系对于材料强度和工程设计具有重要意义。
应力是指物体内部的力,可以描述为单位面积上施加的力。
它通常用符号σ(sigma)表示,单位为帕斯卡(Pa)。
应力可以分为正应力(tensile stress)和剪应力(shear stress)两种类型。
正应力指作用在物体上的拉伸或压缩力。
拉伸应力是指物体被拉伸的力,压缩应力是指物体被压缩的力。
正应力的大小等于作用力除以物体横截面的面积。
剪应力指作用在物体上的剪切力,是指物体内部各点上的两个互相垂直的力之间的比例。
剪应力的大小等于剪切力除以物体横截面的面积。
应变是指物体对于应力的响应,是单位长度的长度变化。
应变可以描述为物体在单位长度上的变形程度。
应变可以分为线性应变(linear strain)和剪应变(shear strain)两种类型。
线性应变指物体的长度变化与原始长度的比例。
它是一个无量纲的物理量,通常用符号ε(epsilon)表示。
线性应变可以是拉伸应变,也可以是压缩应变。
拉伸应变是指物体在拉伸力作用下产生的应变,压缩应变是指物体在压缩力作用下产生的应变。
剪应变指物体产生的平面变形,在受到平行力作用的情况下,物体的形状会发生变化。
剪应变可以通过一个无量纲数值来表示物体的错位程度。
应力-应变关系应力和应变之间存在一种关系,称为应力-应变关系。
它描述了物体在受到应力作用时的应变程度。
应力-应变关系可以是线性的,也可以是非线性的。
在线性应力-应变关系中,应力和应变之间存在简单的比例关系。
例如,在拉伸应力作用下,当应力增加时,应变也会以同样的比例增加。
这种关系可以由胡克定律(Hooke's law)来描述。
胡克定律是一种线性弹性模型,描述了应力和应变之间的关系。
根据胡克定律,应力与应变之间的比例常数被称为弹性模量(elastic modulus)。