认识的应力与应变的关系

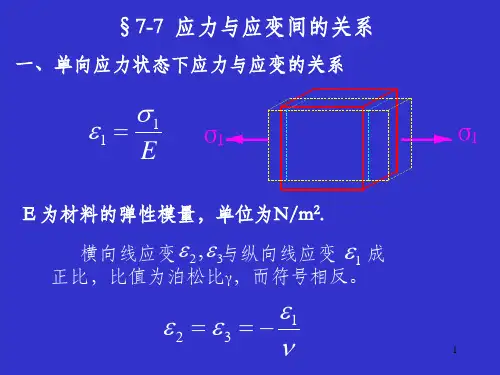
弹性体的应力与应变弹性体是一种在受力作用下可以发生形变，但当受力停止时，能够恢复原来形状和大小的材料。

了解弹性体的应力与应变关系对于工程设计和材料科学具有重要意义。

在本文中，我们将探讨弹性体的应力与应变之间的关系，分析材料的弹性性质以及应力与应变的计算方法。

1. 应力的概念与计算方法应力是指单位面积上作用的力，合理地计算应力是分析弹性体性质的关键。

在计算应力时，常用到两种基本的力学概念：张力和压力。

张力是指沿一维方向的受力情况，通常用F表示，单位为牛顿。

而压力是指在一个平面上均匀分布的力，用P表示，单位是帕斯卡。

应力的计算公式如下：应力 = 受力 / 横截面积2. 应变的概念与计算方法应变是指材料在受力作用下发生的形变，一般用ΔL / L表示。

其中，ΔL是材料长度的变化量，L是材料的初始长度。

应变可以分为线性弹性应变和非线性应变。

线性弹性应变是指材料在受力作用下，形变与受力成正比的状态。

计算线性弹性应变的方法如下：应变 = 形变 / 初始长度而非线性应变则需要更复杂的计算方法来进行分析，涉及到材料的本构关系等。

3. 应力与应变的关系应力与应变之间存在一定的关系，即应力-应变曲线。

弹性体的应力-应变曲线通常可以分为三个阶段：弹性阶段、屈服点和塑性阶段。

在弹性阶段，材料受力时会产生应变，但当受力停止时，材料会完全恢复到原来的状态。

这是因为材料内部的原子或分子只发生了相对位移，而没有发生永久性的结构变化。

当应力超过材料的屈服点时，就进入了屈服点阶段。

在这个阶段中，材料开始发生塑性变形，不再能够完全恢复到原来的状态，具有一定的永久性形变。

塑性阶段是材料的应力与应变不再成正比，继续增加应力会导致更大的应变。

这是由于材料的内部结构发生了永久性的改变，无法恢复原状。

4. 弹性模量和刚度弹性模量是描述材料抵抗形变的能力，可以用来评估材料的刚度。

弹性模量越大，表示材料越难发生形变，具有较高的刚度。

常用的弹性模量有三种：杨氏模量、剪切模量和体积模量。

应力张量和应变张量的关系在物理和工程的世界里，有两个小伙伴总是形影不离，那就是应力张量和应变张量。

就像老鼠和米饭，或者说是鱼和水，这俩家伙其实是相辅相成的，缺一不可。

今天咱们就来聊聊这两位的关系，顺便让这话题变得轻松有趣，让大家听了觉得“这还真有意思！”1. 应力张量——你能忍受多少压力？1.1 什么是应力张量？应力张量嘛，可以简单理解为“压力的图谱”。

想象一下，你在参加一场拔河比赛，另一边的人使劲拉，你的手臂就会感受到拉力。

这个拉力就是应力。

如果我们把这个感觉用一个数学对象来表示，那就是应力张量。

它可以告诉我们在一个物体内部，各个方向上受到了多大的压力。

1.2 应力的分类应力可不是单一的，它分成好几种，像是“拉应力”、“压应力”和“剪应力”。

拉应力就像你拉一根橡皮筋，越拉越长；压应力则像是在面团上用力按，面团就变扁了。

至于剪应力嘛，想象一下你在切水果，刀子刮过的地方就是受到剪应力的地方。

通过这些应力，我们就能感受到物体内部的变化和状态。

2. 应变张量——变形的小精灵2.1 应变张量的概念说到应变张量，它就像是应力张量的反应者，专门负责记录物体是如何变形的。

用个简单的比喻来说，假如应力是拉面师傅的力量，那么应变就是拉出来的面条。

面条在拉伸的过程中，变长了，变细了，这就是应变在作怪。

2.2 应变的种类应变同样有多种形式，比如“拉伸应变”、“压缩应变”和“剪切应变”。

拉伸应变就像你把橡皮筋拉得细细的，压缩应变就像把一个泡沫压扁，而剪切应变就像你用力划过一块巧克力，让它变得不平整。

这些变形的形式让我们对材料的性能有了更深的理解。

3. 应力与应变——亲密无间的关系3.1 他们是好朋友说到应力和应变的关系，其实就是一个因果关系。

就像是“打虎亲兄弟，上阵父子兵”，应力会导致应变的发生。

你想啊，当一个物体受到外力作用时，它肯定会有所反应，这个反应就是应变。

这就像你被朋友拉着走，脚步肯定要跟着他的节奏走，这样才能保持平衡。

应力应变关系我所认识的应力应变关系一在前面两章的分别学习了关于应力与应变的学习，第三章的本构关系讲述了应力与应变的关系从而构成了弹塑性力学的本构关系。

在单向应力状态下，理想的弹塑性材料的应力应变关系及其简单满足胡克定律即,E ,,XX在三维应力状态下需要9个分量，即应力应变需要9个分量，于是可以把单向应力应变关系推广到三维应力状态，及推广到广义的胡克定律本式应该是91个应变分量单由于切应力互等定理，此时后面的三个应力与式中的切应力想等即现在剩余36个应变分量。

(1)具有一个弹性对称面的线弹性体的应力应变公式如下(2)正交各向异性弹性体的弹塑性体公式如下(3)各向同性弹性体的本构方程各向同性弹性体在弹性状态下，主应力方向与主应变方向重合容易证明。

在主应变空间里，由于应变主轴与应力主轴重合，各向同性弹性体体内任意一点的应力和应变之间满足:,,,,,，，CCCxxyz111213,,,,,，，CCCyxyz212223,,,,,，，CCCzxyz313233 (2-3),,,,,,yyxzxz对的影响与对以及对的影响是相同的，即有,CCC==,CC=CC=,y112233x12132123z;和对的影响相同，即，同理有和CC=3132等，则可统一写为:CCCa==,112233CCCCCCb=====,122113312332 (2-4)所以在主应变空间里，各向同性弹性体独立的弹性常数只有2个。

在任意的坐标系中，同样可以证明弹性体独立的弹性参数只有2个。

广义胡可定律如下式,,xy1,,,,,,,,,,，[()]xy,xxyz,2GE,,,,1,yz, ,,，[()],,,,,,,,yzyyxz2GE,,,1,zx,,,,，[()]zx,,,,,,,zzxy,2GE,,EGv泊松比剪切模量 E:弹性模量/杨氏模量 ,2(1),，,,,E虎克定律 ,G,,对于应变能函数理解有点浅在此就不多做介绍了。

2 屈服条件拉伸与压缩时的应力——应变关系曲线P,,A0,ll0,,lBC:屈服阶段,,CD:强化阶段塑性阶段,,DE:局部变形阶段,弹性变形时应力应变关系的特点1.应力与应变完全成线性关系;即应力主轴与全量应变主轴重合2.弹性变形是可逆的，与应变历史(加载过程)无关，即某瞬时的物体形状、尺寸只与该瞬时的外载有关，而与该瞬时之前各瞬间的载荷情况无关。

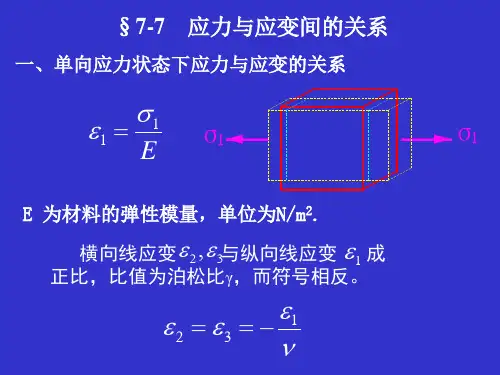
应变与应力的关系
应变与应力的关系可以用胡克定律来描述。

胡克定律指出，在物体恒定温度下，其弹性变形所产生的应变与其所受的应力成正比。

换句话说，应变与应力之间的关系是线性的。

具体来说，该定律的数学表达式为：
应力 = 弹性模量 ×应变
其中，应力是物体所受的力除以其受力面积；弹性模量是物体材料对应力的敏感程度，也称为弹性系数；应变是物体长度、面积或体积的相对变化量。

因此，应变与应力之间的关系是密切相关的。

当施加的应力增加时，物体的应变也会随之增加；反之，当应力减小时，应变也会相应减小。

我所认识的应力与应变的关系机械与动力工程学院我所认识的本构关系可以从三个不同的受力条件下进行分析，第一是在弹性变形下的应力与应变的关系，第二是在屈服条件下的应力与应变的关系，第三是在塑性条件下的应力与应变的关系，而对应力与应变的关系的研究也可以归结为对本构关系的研究。

首先，弹塑性力学分别从静力学和几何学的角度出发，导出了平衡方程的和几何方程，这些方程均与物体的材料性质（物理性质）无关，因而适用于任何连续介质。

但仅仅依靠平衡方程和几何方程来解决实际中的工程问题是不够的。

由于平衡方程仅建立了力学参数（应力分量与外力分量）之间的联系，而几何方程也仅建立了运动学参数（位移分量与应变分量）之间的关系，所以平衡方程与几何方程式两类完全相互独立的方程，他们之间还缺乏必要的联系。

对于所求解的问题来讲，因为您未知量的数目多于任何一类方程的个数，所以无法利用这两类方程求的全部未知量。

平衡方程：⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎭⎫ ⎝⎛∂∂=+∂∂+∂∂+∂∂⎪⎪⎭⎫ ⎝⎛∂∂=+∂∂+∂∂+∂∂⎪⎪⎭⎫ ⎝⎛∂∂=+∂∂+∂∂+∂∂222222000t w Z z y x t v Y z y x t u X z y x z zy zx yz y yx xz xy x ρσττρτστρττσ （1） 几何方程：⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+∂∂=∂∂=∂∂+∂∂=∂∂=∂∂+∂∂=∂∂=x w z u z w z v y w y v y u x v x u zx z yz y xy x γεγεγε （2） 为了求解具体的力学问题，还必须引进一些关系式，这些关系式即所谓的本构关系。

本构关系反映可变形体材料的固有特此那个，故也称为物理关系，它实际上是一组联系力学参数和运动学参数的方程式，即所谓的本构方程。

本构方程实际上就是一组反映可变形体材料应力和应变之间关系的方程。

在单向应力状态下，理想弹性材料的应力和应变之间的关系极其简单。

我所认识的应力应变关系应力应变都是物体受到外界载荷产生的响应。

物体由于受到外界载荷后，在物体内部各部分之间要产生互相之间的力的作用，由于受到力的作用就会产生相应的变形；或者由于变形引起相应的力的作用。

则一定材料的物体其产生的应力和应变也必然存在一定的关系。

一 应力-应变关系影响本构关系的因素有很多，例如材料、环境、加载类型（载荷、温度）、加载速度（动载荷、静载荷）等，当然，本构关系有很多类型，包括弹性、塑性、粘弹性、粘塑性、各向同性、各向异性本构关系，那么首先来叙述一下简单情况本构关系，所谓简单情况就是六个应力分量x y xy yz zx σσστττ、、z 、、、只有一个不为零，六个应变分量x y xy yz zx εεεγγγ、、z 、、、只有一个自由变化，应力应变关系图1-1。

图1-1 应力应变关系图图中OA 为线弹性阶段，AB 为非线弹性阶段，故OB 为初始弹性阶段，C 点位初始屈服点，()s σ+为初始屈服应力，CBA 为弹性阶段卸载，这一阶段中E σε=，初始弹性阶段结束之后，应力继续增大，进入塑性阶段，CDE 为强化阶段，应变强化硬化，EF 为颈缩阶段，应变弱化软化。

如果在进入塑性阶段卸载后再加载，例如在D 点卸载至零，应力应变关系自D 点沿'DO 到达'O 点，且'DO ∥OA ，其中'O O 为塑性应变p ε，DG 为弹性应变e ε，总应变为它们之和。

此后再继续加载，应力应变关系沿ODEF 变化，D 点为后继屈服点，OD 为后继弹性阶段，()'s σ+为后继屈服应力，值得一提的是初始屈服点只有一个，而后继屈服点有无数个（由加载历史决定）。

若在卸除全部载荷后反向加载，弹性阶段'COC ，()()s s σσ+-=，而在强化阶段'DOD ，()()s s σσ+->，称为Bauschinger 效应。

从上述分析得出材料弹塑性行为有一定的特殊性，主要表现在：弹性应力应变关系是线性，且是单值对应关系，而塑性应力应变关系是非线性的非单值对应。

（整理）弹性⼒学第四章应⼒和应变关系第四章应⼒和应变关系知识点应变能原理应⼒应变关系的⼀般表达式完全各向异性弹性体正交各向异性弹性体本构关系弹性常数各向同性弹性体应变能格林公式⼴义胡克定理⼀个弹性对称⾯的弹性体本构关系各向同性弹性体的应⼒和应变关系应变表⽰的各向同性本构关系⼀、内容介绍前两章分别从静⼒学和运动学的⾓度推导了静⼒平衡⽅程，⼏何⽅程和变形协调⽅程。

由于弹性体的静⼒平衡和⼏何变形是通过具体物体的材料性质相联系的，因此，必须建⽴了材料的应⼒和应变的内在联系。

应⼒和应变是相辅相成的，有应⼒就有应变；反之，有应变则必有应⼒。

对于每⼀种材料，在⼀定的温度下，应⼒和应变之间有着完全确定的关系。

这是材料的固有特性，因此称为物理⽅程或者本构关系。

对于复杂应⼒状态，应⼒应变关系的实验测试是有困难的，因此本章⾸先通过能量法讨论本构关系的⼀般形式。

分别讨论⼴义胡克定理；具有⼀个和两个弹性对称⾯的本构关系⼀般表达式；各向同性材料的本构关系等。

本章的任务就是建⽴弹性变形阶段的应⼒应变关系。

⼆、重点1、应变能函数和格林公式；2、⼴义胡克定律的⼀般表达式；3、具有⼀个和两个弹性对称⾯的本构关系；4、各向同性材料的本构关系；5、材料的弹性常数。

§4.1 弹性体的应变能原理学习思路:弹性体在外⼒作⽤下产⽣变形，因此外⼒在变形过程中作功。

同时，弹性体内部的能量也要相应的发⽣变化。

借助于能量关系，可以使得弹性⼒学问题的求解⽅法和思路简化，因此能量原理是⼀个有效的分析⼯具。

本节根据热⼒学概念推导弹性体的应变能函数表达式，并且建⽴应变能函数表达的材料本构⽅程。

根据能量关系，容易得到由于变形⽽存储于物体内的单位体积的弹性势能，即应变能函数。

探讨应变能的全微分，可以得到格林公式，格林公式是以能量形式表达的本构关系。

如果材料的应⼒应变关系是线性弹性的，则单位体积的应变能必为应变分量的齐⼆次函数。

因此由齐次函数的欧拉定理，可以得到⽤应变或者应⼒表⽰的应变能函数。

应力与应变的关系
你想啊，咱们每天上班下班，跟个陀螺似的转个不停，这不就是生活中的“应力”嘛！有时候，老板给的任务多了点，压力山大啊，感觉就像是被压得喘不过气来。

这时候，咱们不能硬扛，得学会“应变”。

比如，合理安排时间，提高工作效率，或者偶尔偷个闲，跟同事开个玩笑，放松放松心情，这不就是咱们应对压力的“应变”小妙招嘛！
再瞅瞅咱们身边的朋友圈，有时候也会遇到点小摩擦，比如意见不合啦，误会啥的。

这时候，如果都死磕着不放，那友谊的小船说翻就翻。

所以啊，咱们得学会变通，学会理解，学会包容，就像弹簧一样，压一下，弹回来，还能更加紧密。

这就是友情里的“应力与应变”，相互磨合，才能更加坚固。

还有啊，咱们对待自己的身体也得这样。

工作再忙，也不能忽视了健康。

不然，身体一出问题，那可就是大问题了。

这时候，咱们得赶紧调整作息，均衡饮食，适当运动，给身体减减压，让它也能“应变”过来，继续活力满满地陪咱们闯荡江湖。

说到底，应力与应变，就像是生活中的一场场小考，考验着咱们的智慧和心态。

咱们不能一味地逃避，也不能硬碰硬，得学会灵活应对，找到最适合自己的方式去化解压力，享受生活的乐趣。

毕竟，人生嘛，就是一场修行，一场关于如何在压力中成长，在变化中前行的修行。

所以啊，下次当你觉得压力山大的时候，不妨换个角度想想，这也许是个机会，让你学会更多，变得更加强大。

毕竟，没有压力，哪来的动力呢？咱们啊，就在这应力与应变的交织中，一步步成长，一步步走向更加美好的未来！。

应力和应变分析应力和应变分析是材料力学中非常重要的一项内容，它们研究材料在外力作用下的变形行为。

应力是表征材料单位面积内的力的大小，而应变则是描述材料单位长度内的变形程度。

应力和应变的分析可以帮助我们理解材料的强度和刚度，以及材料在不同条件下的变形和破坏机制。

本文将从应力和应变的定义、材料的本构关系和应变测量等方面进行探讨。

首先，应力的定义为单位面积内的力的大小，常用符号为σ，其计算公式为σ=F/A，其中F为施加力的大小，A为力作用的面积。

应力的单位通常为帕斯卡（Pa），1Pa等于1N/m^2、根据作用力的不同方向，应力又可以分为正应力和剪应力。

正应力是垂直于材料截面的力，剪应力则是在材料截面上平行于切平面的力。

其次，应变是材料受力后发生的形变程度，常用符号为ε，其计算公式为ε=ΔL/L0，其中ΔL为长度的增量，L0为力作用前的长度。

应变的单位为无量纲。

类似于应力，应变也有正应变和剪应变之分。

正应变是材料在力作用下产生的沿体积方向的变化，剪应变则是在截面上平行于剪切力方向的变化。

应力和应变之间的关系可以通过材料的本构关系来描述。

材料的本构关系是材料在应力与应变之间的函数关系，通常以应力-应变曲线的形式表示。

根据材料的性质不同，应力-应变曲线可以分为线性区、弹性区、屈服区、塑性区和断裂区。

在线性区内，应力和应变呈线性关系，材料具有良好的弹性行为。

在弹性区内，材料回复到原始形状，没有永久性变形。

当应力超过一定的值时，材料进入屈服区，出现塑性变形。

塑性区内，材料的应变增大，但没有太大的应力增加。

当材料无法再承受应力引起继续塑性变形时，出现断裂。

最后，应变的测量是应力和应变分析的重要一环。

常用的应变测量方法包括拉伸试验、剪切试验、压缩试验等。

拉伸试验是最常见的应变测量方法之一，通过施加拉力来测量材料在不同应力下的应变。

剪切试验则是通过施加剪切力来测量材料的剪切应变。

压缩试验则是将材料压缩后测量其压缩应变。

力学应力与应变的名词解释力学是研究物体受力时的运动和相互作用的学科，它探索了自然界中物体的运动规律以及力的作用方式。

力学中的一个重要概念是应力和应变，它们描述了物体受力后的状态和变形程度。

本文将解释并探讨这两个名词的含义，并探索它们在力学中的重要性和应用。

1. 应力应力是指物体在受到力的作用下，单位面积上所承受的力的大小。

单位为帕斯卡（Pa），常用符号为σ。

应力分为三种类型：拉应力、压应力和剪应力。

拉应力是指物体受到沿着其长度方向作用的力而产生的应力，例如，当我们拉伸一根橡皮筋时，橡皮筋上的拉应力就会增加。

压应力则是指物体受到垂直于其表面方向的压力而产生的应力，类似地，当我们挤压一块海绵时，海绵表面上的压应力也会增加。

剪应力是指物体受到平行于其表面方向的切力而产生的应力，当我们用剪刀剪断纸张时，纸张表面就会受到剪应力。

应力的大小取决于应力的作用方向、物体的形状和力的大小。

对于同一物体，应力越大，物体越难以抵抗外界力的作用，导致可能发生破坏。

2. 应变应变是物体在受到应力作用后发生的形变程度。

它描述了物体受力后的变形情况。

应变是一个无量纲的物理量，通常以ε表示。

应变可以分为线性应变和切变应变两种类型。

线性应变是指物体在受到拉应力或压应力时，沿着应力方向发生的长度变化。

它可以通过物体的初始长度和变化后的长度之差来计算。

例如，拉伸一个橡皮筋时，橡皮筋的长度将发生增加，这就是线性应变的一种表现形式。

切变应变是指物体在受到剪应力作用时，物体内部各层之间的相对移动导致的形变。

我们可以通过物体上两点之间的相对位移来计算切变应变。

当我们用剪刀剪断纸张时，纸张的形变就是切变应变的结果。

3. 应力与应变的关系应力与应变之间存在着一定的关系，这种关系用作力学材料的特性描述很重要。

弹性模量是描述应力和应变关系的重要参数。

弹性模量反映了物体在受力时的刚度程度，它用于衡量物体在受力后能够恢复原状的能力。

在弹性范围内，应力和应变成正比。

我所认识的应力与应变关系机械与动力工程学院张淑颖612080706053在弹塑性力学中，可变性固体在外力作用下将发生变形。

根据变形的特点，固体在受力过程中的力学行为可分成两个明显不同的阶段：当外力小于某一限值（通常称之为弹性极限荷载）时，在引起变形的外力卸载后固体能完全恢复原来的形状，这种能恢复的变形成为弹性变形，固体只产生弹性变形的阶段成为弹性阶段；外力一旦超过弹性极限荷载，这时再卸除和在，固体也不能恢复原状，其中有部分不能消失的变形被保留下来，这种保留下来的永久变形就成为塑性变形，这一阶段成为塑性阶段。

在弹性阶段，应力和应变之间存在一一对应的单值函数关系，而且还假设是线性关系；在塑性阶段，应力和应变之间通常不存在一一对应的关系，而且通常还是非线性关系（这种非线性成为物理非线性）。

构成实际固体的材料种类很多，它们的性质各有差异，为方便研究，往往根据材料的主要性质做出某些假设，在弹性理论中，有如下的基本假设：⑴假设物体是连续的。

物体内部由连续介质组成，物体中没有空隙，因此物体中的应力、应变、位移等量是连续的，可以用坐标的连续函数表示。

⑵假设物体是均匀的。

整个物体是由同一材料组成的，所有各部分具有相同的弹性，物体弹性常数不随位置坐标而变，可以取出该物体的任意一小部分来加以分析，然后把分析的结果应用于整个物体。

⑶假设物体是各向同性的。

物体的弹性在所有各个方向都相同，物体的弹性常数弹性模量、泊松系数不随方向而变。

显然，木材和竹材的构件都不能当做各向同性体。

至于钢材的构件，虽然含有各向异性的晶体，但由于晶体很微小，而且是随机排列的，因此钢材构件的弹性包含无数多微小晶体随机排列时的统观弹性大致是各向同性的。

⑷假设物体是完全弹性的。

凡是符合以上四个假定的物体，就称为理想弹性体。

⑸假设位移和应变是微小的。

假定物体受力以后，整个物体所有各点的位移都远远小于物体原来的尺寸，并且应变和转角都远小于。

这样，在建立物体变形以后的平衡方程时，就可以用变形以前的尺寸来代替变形以后的尺寸，而不致引起显著的误差。

我所认识的应力和应变之间的关系在单向应力状态下，理想弹性材料的应力和应变之间的关系是满足胡克定律的一一对应的关系。

在三维应力状态下描述一点处的应力状态需要9个分量，相应的应变状态也要用9个应变分量来表示。

对于一个具体的理想弹性体来讲，如果在三维应力状态下，应力与应变之间仍然有线性一一对应关系存在，则称这类弹性体为线性弹性体。

所谓各向弹性体，从力学意义上讲，就是弹性体内的每一点沿各个方向的力学性质都完全相同的。

这类线性弹性体独立的唐兴常数只有两个。

各向同性体本构关系特点：1.主应力与主应变方向重合。

2.体积应力与体积应变成比例。

3.应力强度与应变强度成比例。

4.应力偏量与应变偏量成比例。

工程应用中，常把各向同性弹性体的本构方程写下成11()11()11()x y z xy xy y x z yz yz z y x xz xz E G E G E G εσμσσγτεσμσσγτεσμσσγτ⎧⎡⎤=-+=⎣⎦⎪⎪⎪⎡⎤=-+=⎨⎣⎦⎪⎪⎡⎤=-+=⎪⎣⎦⎩，式中分别为弹性模量、泊松比和剪切模量。

在E G μ、、这三个参数之间，实际上独立的常量只有两个，它们之间存在关系为()21E G μ=+。

屈服条件:弹性和塑性的最主要区别在于变形是可以恢复。

习惯上，根据破坏时变形的大小把工程材料分为脆性材料和塑性材料两类。

对于加载过程如图1OA: 比例阶段；线性弹性阶段AB: 非弹性变形阶段 BC ： 初始屈服阶段 s σσ≤ CDE ：强化阶段；应变强化硬化阶段EF ： 颈缩阶段；应变弱化，软化阶段s σσ≥ C 点为初始屈服点具有唯一性。

在应力超过屈服应力后，如果在曲线上任意一点D 处卸载，应力和应变之间将不再遵循原有的加载曲线规律，而是沿一条接近平行于OA 的直线DO ’变化，直到应力下降为零，这时应变并不为零，即有塑性应变产生。

如果用OD ’表示总应变ε，O ’D ’表示可以恢复的弹性应变eε，OO ’表示不能恢复的塑性应变p ε，则有e p εεε=+，即总应变等于弹性应变加上塑性应变。

应力和应变1. 简介在力学和材料科学中，应力和应变是两个重要的概念。

应力是指材料内部受到的力的作用，而应变是指材料在受到力作用后发生的形变。

应力和应变是描述材料力学性能的基本参数，对于材料的设计和工程应用具有重要意义。

2. 应力应力是材料内部受到的力的作用，通常用符号σ表示，其单位是帕斯卡（Pa），也可以使用兆帕（MPa）或千兆帕（GPa）。

应力可以分为三类：正应力、剪应力和法向应力。

2.1 正应力正应力是指作用在材料内部的垂直于截面的力，可以通过力除以截面积来计算。

正应力可以进一步分为拉应力和压应力，分别表示拉伸和压缩材料时的应力。

拉应力表示材料受到拉伸作用时的应力，通常以正数表示。

拉应力会使材料发生形变，具有延展性和弹性，可以恢复原状。

压应力表示材料受到压缩作用时的应力，通常以负数表示。

压应力会使材料发生形变，具有收缩性和塑性，并且不易恢复原状。

2.2 剪应力剪应力是指作用在材料内部的平行于截面但方向不同的力，可以通过力除以截面积来计算。

剪应力会使材料发生扭转和剪切形变。

剪应力会产生剪切变形，对应的是材料的剪切模量，可以用于描述材料的硬度和可塑性。

2.3 法向应力法向应力是指作用在材料内部的垂直于截面方向的力，可以通过力除以截面积来计算。

法向应力会使材料发生压缩或拉伸形变。

法向应力的大小和方向取决于施加力的方向和大小，可用于描述材料的稳定性和破坏性。

3. 应变应变是材料在受到力作用后发生的形变，通常用符号ε表示。

应变可以分为线性应变和非线性应变两类。

3.1 线性应变线性应变是指材料在受到小应力作用时，形变与力之间的关系是线性的。

线性应变可以通过材料的弹性模量来描述，弹性模量是材料在小应力作用下恢复原状能力的度量。

3.2 非线性应变非线性应变是指材料在受到大应力作用时，形变与力之间的关系是非线性的。

非线性应变通常发生在超过材料弹性极限时，即材料开始变形并难以恢复原状的阶段。

非线性应变可以引起材料的塑性变形和破坏，对于材料的设计和使用具有重要影响。