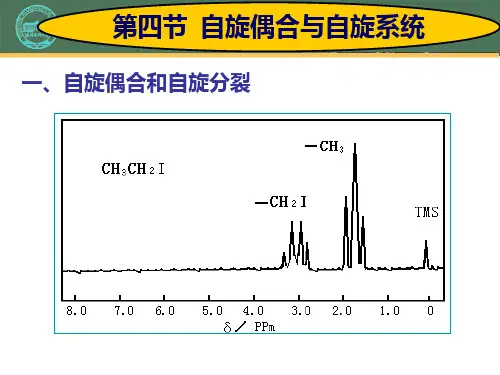
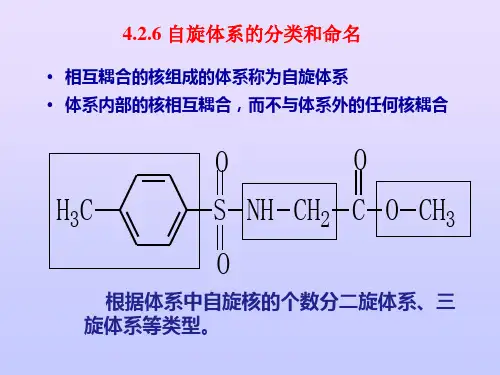
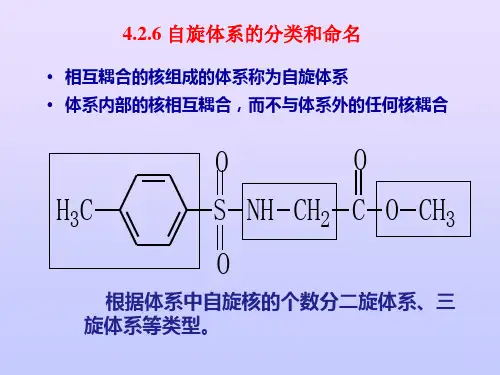
常见的自旋系统
- 格式:ppt
- 大小:3.84 MB
- 文档页数:73


自旋涨落的理论模型与分析引言自旋涨落是指自旋系统在热力学平衡态下产生的涨落现象。
自旋涨落广泛存在于自旋玻璃、自旋涨落液晶等体系中,并被广泛研究和应用。
本文将介绍自旋涨落的理论模型与分析方法。
自旋涨落的基本概念自旋涨落是指自旋系统中自旋的朝向产生微小的随机改变。
在温度为零的条件下,自旋涨落不存在;而在有限温度下,自旋系统由于热运动而呈现涨落现象。
自旋涨落的理论模型自旋涨落的理论模型通常是基于自旋系统的哈密顿量和热力学平衡态下的统计物理学。
常用的理论模型包括伊辛模型、海森堡模型等。
这些模型通常将自旋系统抽象为一个网格,每个网格点上的自旋可以取不同的值,通过哈密顿量来描述自旋之间的相互作用。
然后利用统计物理学的方法,可以得到自旋涨落的性质。
伊辛模型伊辛模型是描述自旋涨落的重要模型之一。
在伊辛模型中,自旋系统被描述为一个二维网络,每个网络节点上的自旋可以取向上或向下两个状态。
伊辛模型的哈密顿量可以写为:$$H = -\\sum_{\\langle i, j \\rangle}J_{ij}s_is_j - \\mu \\sum_is_iB$$其中,$\\langle i, j \\rangle$表示相邻节点对之间的求和,J ij表示自旋之间的相互作用强度,s i表示节点i上的自旋取向,B表示外部磁场强度,$\\mu$表示磁矩。
通过对伊辛模型进行统计物理学的分析,可以得到自旋涨落的各种性质。
海森堡模型海森堡模型是一种描述自旋系统的量子力学模型,常用于描述自旋涨落液晶等体系。
在海森堡模型中,自旋被描述为一个三维矢量,表示自旋的取向和大小。
海森堡模型的哈密顿量可以写为:$$H = -J\\sum_{\\langle i, j \\rangle}\\mathbf{S}_i \\cdot \\mathbf{S}_j - \\mu \\sum_i\\mathbf{S}_i\\cdot\\mathbf{B}$$其中,$\\mathbf{S}_i$表示自旋矢量,$\\langle i, j \\rangle$表示相邻节点对之间的求和,J表示自旋之间的相互作用强度,$\\mathbf{B}$表示外部磁场矢量,$\\mu$表示磁矩。






自旋与量子自旋态自旋是量子力学中一个非常重要的概念,它描述了微观粒子固有的角动量。
自旋的量子性质引发了科学界的广泛兴趣和追求,量子自旋态则是自旋的各种状态。
本文将探讨自旋和量子自旋态的基本概念,并尝试揭示自旋的奇妙之处。
自旋是指微观粒子围绕自身轴线所具有的旋转运动。
不同于传统的角动量,自旋是一个纯量子性质,它没有经典对应物。
自旋可以用一个量子数(通常用s表示)来描述,它可以是整数(例如0, 1, 2, …)或半整数(例如1/2, 3/2, 5/2, …)。
这个量子数决定了自旋的大小和方向。
例如,电子的自旋量子数为1/2,而光子的自旋量子数为1。
自旋的一个重要特征是自旋态,即描述自旋的状态。
在量子力学中,自旋态用波函数表示,波函数可以是自旋的线性组合。
自旋态常用符号表示,例如|↑⟩和|↓⟩分别表示自旋向上和自旋向下。
值得注意的是,这里的“向上”和“向下”只是习惯用语,并没有与空间方向有直接的联系。
自旋态可以是纯态(pure state)或混合态(mixed state)。
在自旋系统中,自旋算符起着重要的作用。
自旋算符用来描述自旋的性质和变化。
自旋算符包括自旋角动量的x、y、z分量的算符,分别表示为Sx、Sy和Sz。
自旋算符的观测值可以是自旋量子数的倍数。
例如,对于自旋量子数为1/2的自旋系统,观测Sx时可能得到±1/2的结果。
自旋的一个重要应用是量子计算。
由于自旋是一个可调控的量子系统,并且具有长时间的相干性,因此自旋可以用来实现量子比特,进而用于量子计算。
量子自旋计算是基于自旋的量子比特的操作,在这种计算中,自旋处于叠加态(superposition)和纠缠态(entanglement)之间,以实现并行计算和量子纠错等重要功能。
除了量子计算,自旋还具有许多其他的应用。
在材料科学中,自旋可以指导新型材料的开发,例如能够实现自旋电子学的材料。
在量子通信中,自旋量子态可以用来传输和存储量子信息。