偏心受压强度验算(矩形和圆形截面)

习题第四章轴心受力4.1 某现浇钢筋混凝土轴心受压柱，截面尺寸为b×h400mm×400mm，计算高度l0 4.2m，承受永久荷载产生的轴向压力标准值N Gk1600 kN，可变荷载产生的轴向压力标准值N Qk1000kN。

采用C35 混凝土，HRB335级钢筋。

结构重要性系数为 1.0。

求截面配筋。

（A s'＝3929 mm2）4.2 已知圆形截面轴心受压柱，直径d=500mm，柱计算长度l0=3.5m。

采用C30 混凝土，沿周围均匀布置 6 根ф20的HRB400纵向钢筋，采用HRB335等级螺旋箍筋，直径为10mm，间距为s=50mm。

纵筋外层至截面边缘的混凝土保护层厚度为c=30mm。

求：此柱所能承受的最大轴力设计值。

（N u ＝3736.1kN）第五章正截面抗弯5.1已知某钢筋混凝土单筋矩形截面梁截面尺寸为b×h=250mm×450mm，安全等级为二级，环境类别为一类,混凝土强度等级为C40，配置HRB335级纵向受拉钢筋4ф16( A S 804mm2)， a s 35 mm。

要求:该梁所能承受的极限弯矩设计值Mu。

（M u ＝94kN-m）5.2已知某钢筋混凝土单跨简支板, 计算跨度为 2.18m, 承受匀布荷载设计值g q6.4kN/m2筋(包括自重),安全等级为二级，混凝土强度等级为C20，配置HPB235级纵向受拉钢筋,环境类别为一类。

要求:试确定现浇板的厚度及所需受拉钢筋面积并配筋。

（板厚80mm，A s＝321 mm2）5.3 已知某钢筋混凝土单筋矩形截面梁截面尺寸为b×h=250mm×500mm，安全等级为二级，环境类别为一类,混凝土强度等级为C20，配置HRB335级纵向受拉钢筋，承受荷载弯矩设计值M=150kN-m。

要求:计算受拉钢筋截面面积。

（A s＝1451 mm2）5.4 已知某钢筋混凝土简支梁,计算跨度5.7m，承受匀布荷载，其中:永久荷载标准值为10kN/m，不包括梁自重),可变荷载标准值为10kN/m,安全等级为二级，混凝土强度等级为C30，配置HRB335级纵向受拉钢筋。

受压矩形与圆形截面柱截面核心的确定班级：03110802 姓名：王庆辉学号：20081202 指导教师：秦晓桐摘要：工程上常见的脆性材料制成的构件（如砖石、混凝土等）其抗拉强度远低于抗压强度，在承受偏心压缩时构件常会因出现拉应力而破坏，将偏心压力大位置控制在截面核心范围内可避免拉应力的出现，本文通过计算得出矩形与圆形柱截面的截面核心范围。

关键词：截面核心；拉应力；偏心受压1.截面核心的形成原因当杆件受偏心压缩时，其内力分量为轴力F N=F弯矩M y=F·z F 和M z=F·y F。

截面上任意一点C（y,z）的正应力为三项的叠加，即利用惯性半径表示方法，有则从式中可以看出正应力分布是y,z的线性函数，令上式中的正应力σ为零，可得中性轴方程(1)该直线在y,z轴上的截距分别为,从上式中可以看出，当偏心压力的作用点（y F，z F）向形心靠近时，中性轴则远离形心。

因此，若想横截面上只有压应力区，只需把偏心压力的位置控制在一定范围之内，使中性轴不与截面相交即可。

这个载荷作用的范围是围绕截面形心的一个区域，称为截面核心。

2.圆形截面核心的求解方法设圆柱横截面如图，截面半径为R ，公式（1）为中性轴方程，该直线的位置关系与点F 的坐标有关。

令中性轴与圆柱横截面相切所得的点F 为其极限位置，即其中i y =i z =，D 为截面圆的直径。

整理后为：上式为圆心在形心的半径为的圆。

当点F 在该圆内部时，中性轴不会与圆截面相交，即圆截面内只有压应力。

3. 矩形截面核心的求解方法矩形截面如图，其惯性半径为,同理;由方程（1）可得中性轴直线的截距分别为：, 同理令中性轴与AB 边重合，,∞;则,，同理当中性轴分别与BC,CD,AD 边重合时得到, ,。

当直线从AB边绕B点旋转到与BC边重合的过程中，会得到一系列不同斜率的过B点的中性轴直线，这些直线均经过B点，将B点坐标（y B,z B）带入中性轴方程（1）可得：（2）式中y B,z B为常数，因此方程（2）所表示的图形为直线，且过点F1、F2。

矩形截面偏心受压构件正截面的承载力计算一、矩形截面大偏心受压构件正截面的受压承载力计算公式 （一）大偏心受压构件正截面受压承载力计算（1）计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件，可以得到下面两个基本计算公式：s y s y c A f A f bx f N -+=''1α （7-23）()'0''012a h A f x h bx f Ne s y c -+⎪⎭⎫ ⎝⎛-=α （7-24）式中： N —轴向力设计值；α1 —混凝土强度调整系数；e —轴向力作用点至受拉钢筋A S 合力点之间的距离；a he e i -+=2η （7-25） a i e e e +=0 （7-26）η—考虑二阶弯矩影响的轴向力偏心距增大系数，按式（7-22）计算；e i —初始偏心距；e 0 —轴向力对截面重心的偏心距，e 0 =M/N ；e a —附加偏心距，其值取偏心方向截面尺寸的1/30和20㎜中的较大者； x —受压区计算高度。

（2）适用条件1) 为了保证构件破坏时受拉区钢筋应力先达到屈服强度，要求(7-27) 式中 x b — 界限破坏时，受压区计算高度，o b b h x ξ= ，ξb 的计算见与受弯构件相同。

2) 为了保证构件破坏时，受压钢筋应力能达到屈服强度，和双筋受弯构件相同，要求满足：'2a x ≥ (7-28) 式中 a ′ — 纵向受压钢筋合力点至受压区边缘的距离。

（二）小偏心受压构件正截面受压承载力计算（1）计算公式根据力的平衡条件及力矩平衡条件可得s s s y c A A f bx f N σα-+=''1 （7-29）⎪⎭⎫ ⎝⎛'-+⎪⎭⎫ ⎝⎛-=s s y c a h A f x h bx f Ne 0''012α （7-30） ()'0''1'2s s s s c a h A a x bx f Ne -+⎪⎭⎫⎝⎛-=σα （7-31）式中 x — 受压区计算高度，当x ＞h ，在计算时，取x ＝h ；σs — 钢筋As 的应力值，可根据截面应变保持平面的假定计算，亦可近似取：y b s f 11βξβξσ--=(7-32)要求满足：y s y f f ≤≤σ'x b — 界限破坏时受压区计算高度，0h x b b ξ=；— 分别为相对受压区计算高度 x/h 0和相对界限受压区计算高度x b /h 0 ； ′— 分别为轴向力作用点至受拉钢筋A s 合力点和受压钢筋A s ′合力点之间的距离 a he e i -+=2η (7-33) ''2a e he i --=η (7-34) （2）对于小偏心受压构件当bh f N c >时，除按上述式（7-30）和式（7-31）或式（7-32）计算外，还应满足下列条件：()()s s y c a a h A f h h bh f e e a h N -+⎪⎭⎫⎝⎛-≤⎥⎦⎤⎢⎣⎡---'0''00'22 (7-35 )式中 — 钢筋合力点至离纵向较远一侧边缘的距离，即s a h h -='0。

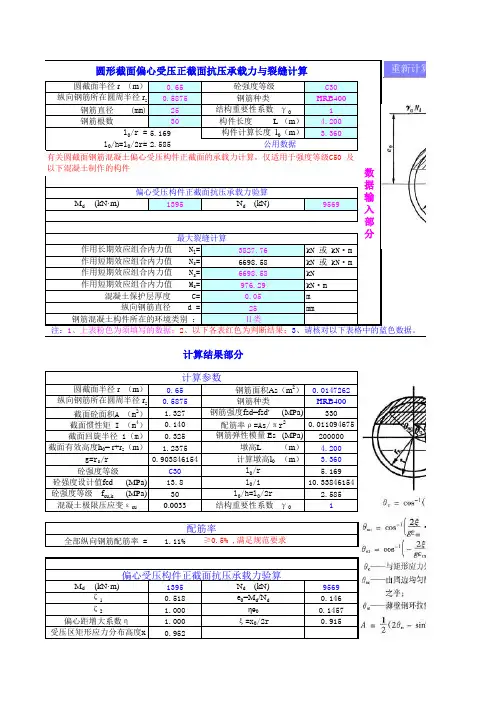
计算结果部分2.4640738410.4635307782546.2(2)3827.76kN 或 kN·m 6698.58kN 或 kN·m 6698.58kN 976.29kN·m 0.65m0.01109530MPa 0.146m1.0142钢筋应力-106.2Mpa 钢筋应力≤24MPa，不必验算裂缝200000Mpa 50mm 1.01.28625mm 钢筋弹性模量 E s =混凝土保护层厚度 C=钢筋表面形状系数 C 1=作用长期效应影响系数 =纵向钢筋直径 d=作用短期效应组合内力值 M s =构件截面半径 r=纵向受拉钢筋配筋率 ρ=As/πr 2=混凝土立方体抗压强度标准值 f cu,k =偏心距 e 0=Ms/Ns=使用阶段轴向力偏心距增大系数裂缝宽度计算 (JTG D62-2004 第6.4.5条)作用长期效应组合内力值 N l =作用短期效应组合内力值 N s =作用短期效应组合内力值 N s =210.5lsN C N =+=+=2000)(/400011hl h e s η=∙⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-=-320,265.10.180.2πr 42.59ρησr e f N s k cu S SS最大裂缝宽度-0.019mm < 0.2 mm,满足Ⅱ类0.20mm最大裂缝宽度限值 ：钢筋混凝土构件所在的环境类别 ：=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=C dE C C w S SS k f 52.1004.003.021ρσ钢筋应力≤24MPa，不必验算裂缝宽度根据“C.0.2-1 的e0=ηe0”用excel菜单"工具->单变量求解" 可快速解得ξ< 0.2 mm,满足规范要求。

一、计算简图：如图。

二、基本假定：
１横截面变形符合平面假定，混凝土最大压应变取εhmax=0.0033。

２混凝土压应力采用等效矩形应力图，且达到抗压设计强度fcd，换算受压区高度采用ｘ=βｘ（ｘ为实际受压区高度），换算系数β与ξ有关：当ξ≤1时β=0.8；当1＜ξ≤1.5时β=1.067-0.267ξ；当ξ＞1.5时，按全截面混凝土均匀受压处理。

３沿圆截面周边布置的钢筋应力依应变而定
σs=εs×Ｅs
４不考虑受拉区混凝土参加工作，拉力全部由钢筋承担。

三、基本方程
四、计算方法：
《公桥规》(JTJ023-85)采用了一种简化了的计算方法--等效钢环法。

混凝土强度等级C50以下的，沿周边均匀配置纵向钢筋的圆形截面钢筋混凝土偏心受压构件，如图所示，
1、计算公式
2、配筋设计
已知：截面的尺寸已知，求钢筋的截面积并进行配筋。

①假定ξ值，查表求出系数A、B、C、D；
②将A、B、C、D代入
算出初始配筋率；
③将μ值代入
进行试算，按程序①～③反复进行，直到满足为止。

求钢筋截面积As=ρ×π×γ2
并配筋。

3、强度复核
①设ξ值，查表求得A、B、C、D。

②将A、B、C、D值代入上式求ηｅ01，按①～②反复计算直至ηｅ0i≈ηｅ0为止。

③将相应于ηｅ0i的ξ值的系数A、B、C、D代入
进行强度复核。

矩形截面偏心受压构件正截面的承载力计算一、矩形截面大偏心受压构件正截面的受压承载力计算公式 （一）大偏心受压构件正截面受压承载力计算（1）计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件，可以得到下面两个基本计算公式：s y s y c A f A f bx f N -+=''1α （7-23）()'0''012a h A f x h bx f Ne s y c -+⎪⎭⎫ ⎝⎛-=α （7-24）式中： N —轴向力设计值；α1 —混凝土强度调整系数；e —轴向力作用点至受拉钢筋A S 合力点之间的距离；a he e i -+=2η （7-25） a i e e e +=0 （7-26）η—考虑二阶弯矩影响的轴向力偏心距增大系数，按式（7-22）计算；e i —初始偏心距；e 0 —轴向力对截面重心的偏心距，e 0 =M/N ；e a —附加偏心距，其值取偏心方向截面尺寸的1/30和20㎜中的较大者； x —受压区计算高度。

（2）适用条件1) 为了保证构件破坏时受拉区钢筋应力先达到屈服强度，要求b x x ≤ (7-27)式中 x b — 界限破坏时，受压区计算高度，o b b h x ξ= ，ξb 的计算见与受弯构件相同。

2) 为了保证构件破坏时，受压钢筋应力能达到屈服强度，和双筋受弯构件相同，要求满足：'2a x ≥ (7-28) 式中 a ′ — 纵向受压钢筋合力点至受压区边缘的距离。

（二）小偏心受压构件正截面受压承载力计算（1）计算公式根据力的平衡条件及力矩平衡条件可得s s s y c A A f bx f N σα-+=''1 （7-29）⎪⎭⎫ ⎝⎛'-+⎪⎭⎫ ⎝⎛-=s s y c a h A f x h bx f Ne 0''012α （7-30） ()'0''1'2s s s s c a h A a x bx f Ne -+⎪⎭⎫⎝⎛-=σα （7-31）式中 x — 受压区计算高度，当x ＞h ，在计算时，取x ＝h ；σs — 钢筋As 的应力值，可根据截面应变保持平面的假定计算，亦可近似取：y b s f 11βξβξσ--=(7-32)要求满足：y s y f f ≤≤σ'x b — 界限破坏时受压区计算高度，0h x b b ξ=；b ξξ、 — 分别为相对受压区计算高度 x/h 0和相对界限受压区计算高度x b /h 0 ；'e e 、′— 分别为轴向力作用点至受拉钢筋A s 合力点和受压钢筋A s ′合力点之间的距离 a he e i -+=2η (7-33) ''2a e he i --=η (7-34) （2）对于小偏心受压构件当bh f N c >时，除按上述式（7-30）和式（7-31）或式（7-32）计算外，还应满足下列条件：()()s s y c a a h A f h h bh f e e a h N -+⎪⎭⎫⎝⎛-≤⎥⎦⎤⎢⎣⎡---'0''00'22 (7-35 )式中 '0h — 钢筋's A 合力点至离纵向较远一侧边缘的距离，即s a h h -='0。

基本构件计算不对称配筋矩形截面偏心受压构件正截面
计算
（一）偏心受压构件正截面计算原理及步骤
1、偏心受压构件正截面计算原理：偏心受压构件的正截面计算是指分析偏心受压构件的正截面，根据受力原理、承载力理论等原理，使用有限元分析方法和有限元程序，即设计必要的有限元划分和边界条件，求得偏心受压构件的正截面应力分布、节点位移及结构安全性等结果。

2、偏心受压构件正截面计算步骤：
（1）构件几何特征分析：分析构件的几何形状及尺寸，包括截面形状、尺寸，材料特性，偏心距、荷载位置、偏心向量等特征。

（2）建立有效的有限元程序：根据构件的几何特征，建立有效的有限元程序，确定有限元单元的类型及节点位置，设计节点或网格的尺寸，确定边界条件等。

（3）计算结果处理：将所有计算结果从节点处理，绘制应力分布曲线，求取偏心受压构件正截面的有效截面系数、最大截面应力、节点位移等性能参数。

（4）模型校核：根据构件的形状、偏心距、荷载位置等，比较试验数据和计算结果，可以很好地判断构件结构的安全性能。

第一节一、普通箍筋柱二、螺旋箍筋柱以承受轴向压力为主的构件称为受压构件。

凡荷载的合力通过截面形心的受压构件称之为轴心受压构件(compression members with axial load at zero eccentricity)。

若纵向荷载的合力作用线偏离构件形心的构件称之为偏心受压构件。

受压构件（柱）往往在结构中具有重要作用，一旦产生破坏，往往导致整个结构的损坏，甚至倒塌。

按箍筋作用的不同，钢筋混凝土轴心受压构件可分为两种基本类型：一种为配有纵向钢筋及普通箍筋的构件，称为普通箍筋柱(tied columns),如图；另一种为配有纵向钢筋及螺旋箍筋或焊环形箍筋的螺旋箍筋柱(spirally reinforced columns)，如图。

一、普通箍筋柱（一）构造要点1、截面形式：正方形、矩形、工字形、圆形；2、截面尺寸：根据正压力、柱身弯距来确定，截面最小边长不宜小于250mm；3、纵筋：（1）纵向受力钢筋的直径不应小于12mm，其净距不应小于50mm，也不应大于350mm，根数不少于４根。

（2）构件的全部纵向钢筋配筋率不宜超过5%。

构件的最小配筋率不应小于0.5%，当混凝土强度等级为C50及以上时不应小于0.6%；同时，一侧钢筋的配筋率不应小于0.2%。

（3）纵向受力钢筋应伸入基础(foundations)和盖梁(caps)，伸入长度不应规定的锚固长度。

4、箍筋：（1）箍筋应做成封闭式，以保证钢筋骨架的整体刚度。

（2）箍筋间距应不大于纵向受力钢筋直径的15倍且不大于构件横截面的较小尺寸(圆形截面采用0.8倍直径)且不大于400mm。

纵向受力钢筋搭接范围的箍筋间距，当绑扎搭接钢筋受拉时不大于主钢筋直径的5倍且不大100mm；当搭接钢筋受压时不大于主钢筋直径的10倍且不大于200mm。

纵向钢筋截面面积大于混凝土截面面积3%时，箍筋间距不应大于纵向钢筋直径的10倍且不大于200mm。

（3）箍筋直径不小于8mm且不小于纵向钢筋直径的1/4。

圆形截面偏心受压构件配筋计算1.首先，确定构件的受力情况，包括受力方向、受力大小和偏心距离等参数。

这些参数将影响到钢筋的配筋计算。

2.根据构件的几何形状，确定构件的截面面积、惯性矩和抗扭矩等参数。

这些参数将用于计算钢筋的布置和数量。

3.计算构件的轴心受力。

根据受力方向和大小，结合偏心距离，计算出构件的轴向受力大小。

这将作为后续配筋计算的依据。

4.根据计算得到的轴向受力大小，通过挠度控制和承载力控制两种设计方法，选取合适的设计假设来确定构件的截面尺寸。

这一步骤是根据具体的设计规范来进行的，不同的规范可能有不同的要求。

5.确定构件的受力范围和影响长度。

这一步骤是根据构件的长度和受力情况来确定的，它将影响到计算所需的横向钢筋的数量和布置。

6.根据受力范围和影响长度，计算构件的配筋面积。

根据设计规范的要求，计算出构件所需的横向钢筋的最小面积。

这一步骤主要是根据受力情况和构件的尺寸来进行的。

7.根据配筋面积，确定横向钢筋的布置。

根据设计规范的要求，确定钢筋的间距和层数，并进行布置。

8.检查构件的设计是否满足强度和稳定性要求。

这一步骤主要是通过计算钢筋的屈服强度和构件的抗压能力来进行的。

9.如果计算结果不满足设计要求，需要调整设计参数，重新进行计算，直至满足要求为止。

需要注意的是，上述步骤是一般情况下的配筋计算步骤，具体计算还需要依据具体的设计规范和构件的受力情况来确定。

此外，需要遵守相应的国家和地区的建筑设计规范和标准，以确保结构的安全和稳定。

矩形和圆形截面重力式桥墩台双向偏心受压下截面极限承载力
实用计算方法
朱尔玉;李廷春
【期刊名称】《铁道标准设计》
【年(卷),期】2004(000)003
【摘要】通过对影响矩形和圆形截面重力式桥墩台在双向偏心受压下截面极限承载力计算结果的多元回归分析,给出一种简单、实用且能满足工程精度要求的计算公式.
【总页数】2页(P5-6)
【作者】朱尔玉;李廷春
【作者单位】北京交通大学土建学院,北京,100044;铁道建筑研究设计院,北
京,102600
【正文语种】中文
【中图分类】U443.21;U443.22
【相关文献】
1.圆形截面钢筋混凝土偏心受压构件正截面强度实用计算方法 [J], 徐文平;徐金法
2.双向偏心受压下圆端形重力式桥墩台极限承载力的计算 [J], 朱尔玉;刘磊;海潮
3.矩形截面重力式桥墩台双向偏心受压下截面极限承载力计算的等效面积法 [J], 朱宗平
4.矩形和圆形截面重力式桥墩极限承载力折减系数的计算方法 [J], 徐艳秋;许克宾
5.圆形截面钢筋混凝土偏心受压构件正截面强度实用计算方法 [J], 徐金法;徐文平因版权原因，仅展示原文概要，查看原文内容请购买。

计算结果部分1.744507717(2)1338kN 或kN·1439kN 或kN·1439kN 282kN·m 0.5m 0.00648025MPa 0.196m 1.0000钢筋应力-35.3Mpa 钢筋应力≤24MPa，不必验算裂缝200000Mpa 30mm 1.01.46518mm 偏心距 e 0=Ms/Ns=裂缝宽度计算 (JTG D62-2004 第6.4.5条)作用长期效应组合内力值 N l =作用短期效应组合内力值 N s =作用短期效应组合内力值 N s =作用短期效应组合内力值 M s =纵向受拉钢筋配筋率 ρ=As/πr 2=混凝土立方体抗压强度标准值 f cu,k =使用阶段轴向力偏心距增大系数钢筋弹性模量 E s =作用长期效应影响系数 =纵向钢筋直径 d=构件截面半径 r=混凝土保护层厚度 C=钢筋表面形状系数 C 1=210.5l s N C N =+=+=2000)(/140011h l h e s η=•⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-=-320,265.10.180.2πr 42.59ρησr e f N s k cu S SS =⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=C d E C C w S SSk f 52.104.003.021ρσ最大裂缝宽度0.003mm < 0.2 mm,满足规范要求Ⅰ类0.20mm钢筋混凝土构件所在的环境类别 ：最大裂缝宽度限值 ：=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=C d E C C w S SSk f 52.104.003.021ρσ根据“C.0.2-1 的e0=ηe0”用excel菜单"工具->单变量求解" 可快速解得ξ。