第26.2讲 波的叠加、驻波的形成、驻波方程
- 格式:ppt
- 大小:696.00 KB
- 文档页数:13







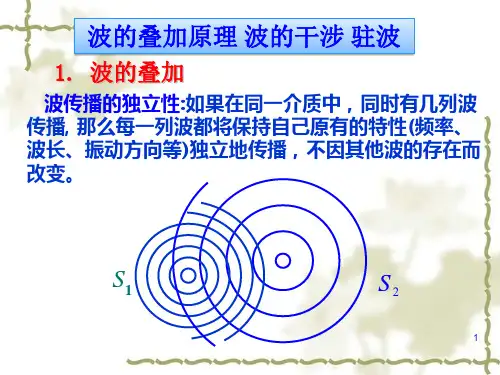


§12-8 波的叠加研究几列波同时在介质中传播时,在空间相遇时的情况.一、波传播的独立性传播方向相反的两个脉冲的叠加由演示看出两列波相遇之后,仍然保持它们各自原有的特征(频率、波长、振幅、振动方向等不变),不受其它波的影响,就像其它波不存在一样。
生活实例:➢红绿光束空间交叉相遇(红是红、绿是绿,…)➢听乐队演奏(仍可辨出不同乐器的音色、旋律)➢空中无线电波很多(仍能分别接收各个电台)二、波的叠加原理在几列波相遇而互相交叠的区域中,某点的振动是各列波单独传播时在该点引起的振动的合成。
三、波的干涉1.干涉现象当两列(或几列)满足一定条件(相干条件)的波在某区域同时传播时,则此区域中某些点的振动始终加强,某些点的振动始终减弱,在空间形成一幅稳定的强度分布图样。
干涉现象水波的干涉2.相干条件满足下列条件的波源称相干波源。
相干波源发的波相干波。
在现实中要产生明显的干涉现象,上述条件只能算必要条件,如果两波源的振幅相差悬殊,将导致干涉现象的可见度降低。
1)频率相同2)有恒定的相位差3)振动方向相同相干条件:1s 2s P *1r 2r 波源振动方程)cos(1011ϕω+=t A y )cos(2022ϕω+=t A y 四、干涉波的强度分布S 1、S 2发的波在p 点引起两个振动)π2cos(11011λϕωr t A y p -+=)π2cos(22022λϕωr t A y p -+=λπϕϕϕ∆121020r -r 2--=相位差可见,两个波源在p 点引起的分振动:频率相同;振动方向相同;相位差恒定(不随t 变)。
p 点合振动是两个同方向、同频率简谐振动的合成。
p 点合振动叫两波波程差12r r -)cos(021ϕω+=+=t A y y y p p p) 2cos() 2cos()2sin() 2sin(tan 22021101220211010λπϕλπϕλπϕλπϕϕr A r A r A r A -+--+-=由同方向同频率简谐振动的合成可以得两相干波叠加后的强度12122cos I I I I I ϕ=+∆+211∝A I 222∝A I由于在相干波的相遇点有确定的相位差∆ϕ,所以每一点都有确定的强度,干涉区域形成了稳定的强度分布。
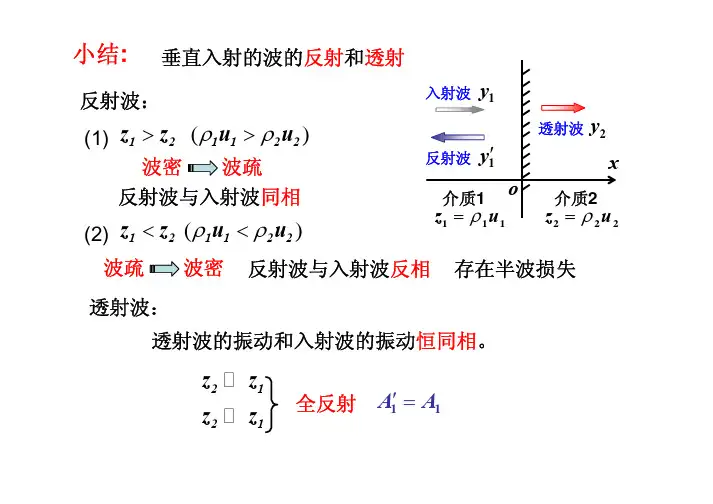
入射波和反射波合成的驻波方程驻波是波动现象中的一种特殊形式,它是由两个同频率、同振幅的波相互叠加而形成的。
这两个波分别是入射波和反射波。
入射波是由外部源产生、传播到介质中的波,而反射波则是由介质边界上的反射产生的波。
当入射波和反射波在介质中相遇时,它们会发生干涉现象,形成驻波。
驻波方程描述了驻波的形态,它是通过将入射波和反射波的振动方程相加而得到的。
驻波方程的形式可以表示为y(x, t) = 2Acos(kx)cos(ωt),其中A表示振幅,k表示波数,x表示空间坐标,ω表示角频率,t表示时间。
这个方程说明了驻波的振幅是随着空间坐标和时间的变化而变化的。
驻波方程中的第一项2Acos(kx)表示了波的空间分布,它是由入射波和反射波的振动相长叠加形成的。
这一项的振幅是2A,表示振幅的加倍效应。
而cos(kx)则表示了波的空间分布,它随着空间坐标的变化而变化,在介质中形成驻波的节点和腹部。
驻波方程中的第二项cos(ωt)表示了波的时间分布,它随着时间的变化而变化,在介质中形成驻波的稳定振动。
这一项的振幅是恒定的,不随时间的变化而变化。
驻波方程描述了驻波的空间和时间特征,它可以用来分析驻波的性质和行为。
通过解析驻波方程,可以得到驻波的振幅、波长、频率等参数。
驻波是一种重要的物理现象,在许多领域中都有应用。
例如,在声学中,驻波可以解释声波在管道、弦线等介质中的传播和共振现象。
在光学中,驻波可以解释光波在光纤、薄膜等介质中的传播和干涉现象。
在电磁学中,驻波可以解释电磁波在导线、天线等介质中的传播和驻波现象。
驻波方程描述了驻波的形态和特征,它通过入射波和反射波的叠加得到。
驻波方程在物理学中有着广泛的应用,可以用来解释和分析驻波现象。
通过研究驻波方程,可以深入理解驻波的本质,并在实际应用中发挥作用。