角平分线定理专题

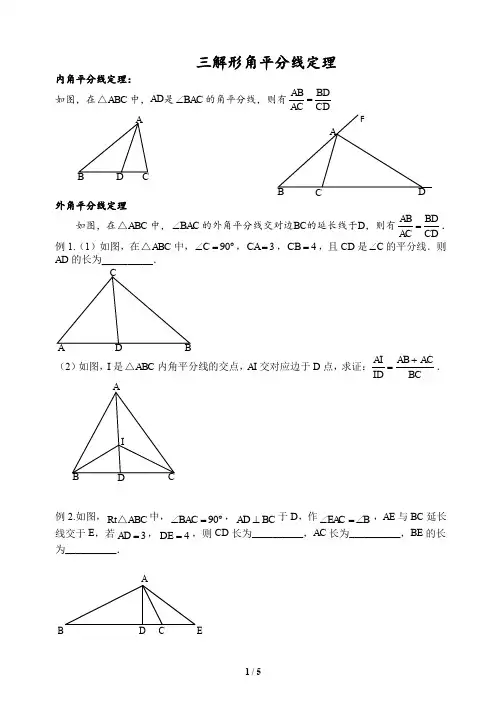
专题18 角平分线定理 一．选择题（共8小题） 1．在ABC中，2AB，73AB，4BC，CD平分ACB交AB于点D，则线段AD

的长为( ) A．1 B．23 C．12 D．13 2．已知在ABC中，内角A，B，C的对边分别为a，b，c，AD是BAC的平分线，2CDBD，2b，则(c )

A．2 B．1 C．3 D．2 3．在ABC中，已知BAC的平分线交BC于点M，且:2:3BMMC．若60AMB，

则(ABACBC ) A．2 B．5 C．7 D．3 4．ABC中，点D在AB上，CD平分ACB．若CAa，CBb，||2a，||1b，则(CD )

A．1233ab B．2133ab C．3455ab D．4355ab 5．在ABC中，角A，B，C所对的边分别为a，b，c，120ABC，ABC的平分线交AC于点D，且1BD，则4ac的最小值为( ) A．8 B．9 C．10 D．7

6．在ABC中，角A，B，C的对边分别为a，b，c，且3sin()32cBa，20CACB，7c，则ABC的内切圆的半径为( ) A．2 B．1 C．3 D．3 7．设I为ABC的内心，延长线段AI交线段BC于点D，若3CDDB，则sin:sin(BC ) A．2:1 B．3:1 C．4:1 D．9:1

8．ABC中，1cos8A，4AB，2AC，则A的角平分线AD的长为( ) A．22 B．23 C．2 D．1 二．填空题（共9小题） 9．在ABC中，角A，B，C的对边分别是a，b，c，已知60A，6bc，且ABC

的面积为3，则ABC的内切圆的半径为 ． 10．在ABC中，58ac，60B，其内切圆半径为3，则其外接圆半径为 ． 11．设I为ABC的内心，三边长7AB，6BC，5AC，点P在边AB上，且2AP，若直线IP交直线BC于点Q，则线段QC的长为 ．

（2）如图 1-2，I 是 △ABC 内角平分线的交点，AI 交对应边于 D 点，求证：AI AB AC ． ID BC
A C
I
A
D
B
图 1-1
B
D
C
图 1-2
解：（1）由角平分线定理得到 AD AC 3 ， DB BC 4
由于 AB
AC2
CB2
5 ，∴ AD
3 7
AB
15 7
．
（2）由角平分线定理得到 AI AB AC ， ID BD CD
交 CE 于点 F．则 AE 长为____________，AD 长为__________．
C
D F
A
E
B
解： ， ．
3.如图，Rt△ABC 中，ACB ， AC ， AB ，CE AB 于 E，AD 平分 BAC 交 CE 于点 F．则 CF 的值为___________，AD 长为__________．
三解形角平分线定理
内角平分线定理：
如图，在 △ABC 中，AD是 BAC 的角平分线，则有 AB BD AC CD
A
F
A
B
DC
外角平图，在 △ABC 中， BAC 的外角平分线交对边BC的延长线于D，则有 AB BD ． AC CD
例 1.（1）如图，在 △ABC 中，C ，CA ，CB ，且 CD 是 C 的平分线．则 AD 的长为__________．
EF
4/5
C
D F
A
E
B
解： CF AC AB ， EF AE AC
AD CD AC ．
【提示】这道题主要考查特殊的 3，4，5 的直角三角形和角平分线的结论．

一、选择题
1.根据角平分线定理，若一条射线是角的平分线，则它将这个角分为两个：
A.锐角
B.钝角
C.相等的小角（答案）
D.不等的小角
2.在三角形ABC中，若AD是∠BAC的平分线，那么：
A.AB = AC
B.BD = CD（答案）
C.∠B = ∠C
D.AD是BC的中线
3.角平分线定理表明，角的平分线上的点到这个角的两边的距离：
A.相等（答案）
B.不等
C.无法确定
D.与角的大小有关
4.在△PQR中，若RS是∠PQR的平分线，且RS交PQ于点S，那么下列哪个选项是正
确的？
A.PS = QS（答案）
B.∠PRS = ∠QRS
C.RS是△PQR的高
D.RS是△PQR的中线
5.根据角平分线的性质，在△XYZ中，若XY是∠XZY的平分线，那么：
A.XY平分∠XYZ
B.XY平分对边XZ
C.点Y到XZ两边的距离相等（答案）
D.XY是XZ的中垂线
6.在四边形ABCD中，若AC是对角∠BAD的平分线，那么：
A.AB = AD
B.BC = CD
C.点C到AB和AD的距离相等（答案）
D.AC是BD的中线
7.角平分线定理不适用于哪种情况？
A.锐角三角形
B.直角三角形
C.钝角三角形
D.圆形（答案）
8.在△MNO中，若MN是∠NMO的平分线，且MN交NO于点P，那么下列哪个选项
是错误的？
A.点P到MO和NO的距离相等
B.∠PMN = ∠PNM
C.MN是△MNO的高（答案）
D.MN将∠NMO分为两个相等的小角。

锐角平分线的三个定理
锐角平分线的三个定理介绍如下：
1. 角平分线定理
* 定义: 若一个角的平分线与一个直线相交，则相对的两个交点到这个角的两边的距离相等。

* 证明: 通过角的平分线上的任意一点，向角的两边作垂线，由于角的平分线性质，这两个垂线长度相等。

再根据点到直线的距离定义，可证该定理。

* 应用: 在几何证明和构造中，角平分线定理常被用来确定与角平分线相关的线段长度。

2. 锐角定理
* 定义: 锐角平分线与该角的对边所形成的夹角小于90°。

* 证明: 设锐角为α，其平分线与对边形成的角为β。

由于α是锐角，所以0°< α< 90°。

根据角的平分线性质，α/2 < β< 90°。

* 应用: 在解决几何问题时，锐角定理可以用来判断角平分线与对边形成的角度的大小。

3. 余弦定理
* 定义: 在任意三角形ABC中，若AD是角BAC的平分线，则有AB²=BD×BC+BD²-CD²。

* 证明: 根据角平分线的性质，得到AD²=BD×BC+CD×AC，然后通过余弦定理和已知条件可证明上述结论。

* 应用: 余弦定理常被用来确定角平分线上的点到三角形的两边距离的关系。

总结：锐角平分线的三个定理在几何学中具有重要地位，它们在解决与角平分线相关的几何问题时非常有用。

深入理解和掌握这些定理对于提高几何解题能力至关重要。

⾓平分线的性质定理和判定定理（含答案）⼏何专题2：⾓平分线的性质定理和判定定理⼀、知识点(抄⼀遍)：1. ⾓平分线：把⼀个⾓平均分为两个相同的⾓的射线叫该⾓的平分线.2. ⾓平分线的性质定理：⾓平分线上的点，到这个⾓的两边的距离相等. 3. ⾓平分线的判定定理：⾓的内部到⾓的两边距离相等的点在⾓的平分线上. ⼆、专题检测题1. 证明⾓平分线的性质定理.（注意：证明⽂字性命题的三个步骤：①根据题意，画出图形；②写出已知和求证；③写出证明过程.） 2. 证明⾓平分线的判定定理. 3. 定理的⼏何语⾔表⽰（1）⾓平分线的性质定理：∵，∴ . （2）⾓平分线的判定定理：∵，∴ .4. 已知：如图所⽰，BN 、CP 分别是∠ABC 、∠ACB 的⾓平分线，BN 、CP 相交于O点，连接AO ，并延长交BC 于M 求证：AM 是∠BAC 的⾓平分线.5. 如图，已知BE ⊥AC ，CF ⊥AB ，点E ，F 为垂⾜，D 是BE 与CF 的交点，AD 平分∠BAC. 求证：BD=CD.B6. 如图，在Rt △ABC 中，∠C=90°，AC=BC. AD 是∠CAB 的平分线. 求证：AB=AC+CD.7. 如图，∠B=∠C=90°，M 是BC 的中点，DM 平分∠ADC ，求证：AM 平分∠DAB.8. 如图,已知P 是∠AOB 平分线上的⼀点.PC ⊥OA ，PD ⊥OB ，垂⾜分别是点C ，D ，CD 与OP 交于点M. 求证：（1）∠PCD=∠PDC ；（2）OP 是CD 的垂直平分线；（3）OC=OD.O⼏何专题2：⾓平分线的性质定理和判定定理答案1. 证明⾓平分线的性质定理.已知：如图，OC 平分∠AOB ，点P 在OC 上，PD ⊥OA 于点D ，PE ⊥OB 于点E求证: PD=PE证明：∵OC 平分∠ AOB∴∠1= ∠2∵PD ⊥ OA，PE ⊥ OB ∴∠PDO= ∠PEO 在△PDO 和△PEO 中∠PDO= ∠PEO ∠1= ∠2 OP=OP∴△PDO ≌△PEO(AAS) ∴PD=PE2.证明⾓平分线的判定定理.已知：如图,PD ⊥OA ，PE ⊥OB ，点D 、E 为垂⾜，PD ＝PE ．求证：点P 在∠AOB 的平分线上证明: 经过点P 作射线OC ∵ PD ⊥OA ，PE ⊥OB∴∠PDO ＝∠PEO ＝90°在Rt △PDO 和Rt △PEO 中PO ＝PO PD=PE ∴ Rt △PDO ≌Rt △PEO （HL ）∴∠ POD ＝∠POE ∴点P 在∠AOB 的平分线上.3. 定理的⼏何语⾔表⽰（1）⾓平分线的性质定理：∵ OP 平分∠AOB ，DP ⊥OA ，PE ⊥OB ，∴ DP=EP. （2）⾓平分线的判定定理：∵ PD⊥OA，PE⊥OB，PD ＝PE ．∴ OP 平分∠AOB ．OO4.已知：如图所⽰，BN、CP分别是∠ABC、∠ACB的⾓平分线，BN、CP相交于O 点，连接AO，并延长交BC于M求证：AM是∠BAC的⾓平分线.证明：作OE⊥AC，OG⊥AB，OF⊥BC，垂⾜分别为E、G、F.∵BN平分∠ABC，OG⊥AB，OF⊥BC，∴OG=OF.同理可证：OE=OF.∴OG=OE⼜∵OE⊥AC，OG⊥AB，∴AM是∠BAC的⾓平分线.5.如图，已知BE⊥AC，CF⊥AB，点E，F为垂⾜，D是BE与CF的交点，AD平分∠BAC.求证：BD=CD.证明：∵AD平分∠BAC，BE⊥AC，CF⊥AB，∴DF=DE.∵BE⊥AC，CF⊥AB，∴∠DFB=∠DEC=90°. 在△DFB和△DEC中，∠EDC=∠FDBDF=DE∠DFB=∠DEC∴△DFB≌△DEC（ASA）∴BD=CD.6.如图，在Rt△ABC中，∠C=90°，AC=BC. AD是∠CAB的平分线.求证：AB=AC+CD.证明：过点D作DE⊥AB，垂⾜为点E.∵AD平分∠CAB，∴∠CAD=∠BAD.∵DE⊥AB∴∠DEA=90°=∠C.在△CAD和△EAD中，∠CAD=∠BAD，∠DEA=∠C，AD=AD.∴△CAD≌△EAD（AAS）.∴AC=AE，CD=DE.∵AC=BC，∴∠B=∠BAC=45°，∵∠DEB=90°，∴∠EDB=45°=∠B.∴DE=BE,∴CD=BE，∴AB=AE+BE=AC+CD.B7. 如图，∠B=∠C=90°，M 是BC 的中点，DM 平分∠ADC ，求证：AM 平分∠DAB.证明：过点M 作ME ⊥AD ，垂⾜为E ，∵DM 平分∠ADC ，∴∠1=∠2，∵MC ⊥CD ，ME ⊥AD ，∴ME=MC （⾓平分线上的点到⾓两边的距离相等），⼜∵MC=MB ，∴ME=MB ，∵MB ⊥AB ，ME ⊥AD ，∴AM 平分∠DAB （到⾓的两边距离相等的点在这个⾓的平分线上）．8. 如图,已知P 是∠AOB 平分线上的⼀点.PC ⊥OA ，PD ⊥OB ，垂⾜分别是点C ，D ，CD 与OP 交于点M. 求证：（1）∠PCD=∠PDC ；（2）OP 是CD 的垂直平分线；（3）OC=OD.证明：（1）∵OP 平分∠AOB ，PC ⊥OA ，PD ⊥OB ，∴PC=PD ∴∠PCD=∠PDC. （2）∵OP 平分∠AOB ，∴∠COP=∠DOP. ∵PC ⊥OA ，PD ⊥OB ，∴∠PCO=∠PDO=90°，∴∠CPO=∠DPO. ∵PC=PD ，∴△CDP 是等腰三⾓形，∴PM 是等腰三⾓形底边上的中线和⾼线. 即OP 是CD 的垂直平分线. （3）由（2）知，∠CPO=∠DPO. ∴OP 平分∠CPD ，⼜∵CP ⊥OA ，DP 垂直OB ，∴OC=OD （⾓平分线的性质定理）.O。

50 ∵AF∥OD，∴ADGG＝OADF＝153＝1103，则 DG＝1233AD. ∵AD＝ AB·AF＝ 18×5103＝301313，则 DG＝1233×301313＝302313.
课堂精讲
【方法归纳】AE是⊙O的直径，点D，F、E是⊙O上的三点，在① “AD平分∠BAC”，②“OD⊥BC”，③“BC是⊙O的切线”三个论断 中，知一推二．
(3)连接EF，在Rt△BOD中，利用三角函数的定义求出圆的半径， AE，AB的长，再证明EF∥BC，得出∠B＝∠AEF，利用锐角三角 函数的定义求出AF的长，再根据AF∥OD，得出线段成比例， 求出DG的长，然后可求出AD的长，从而可求得DG的长
课堂精讲
【解】(1)证明：如图，连接OD. ∵AD为∠BAC的角平分线， ∴∠BAD＝∠CAD. ∵OA＝OD，∴∠ODA＝∠OAD. ∴∠ODA＝∠CAD.∴OD∥AC. ∵∠C＝90°，∴∠ODC＝90°. ∴OD⊥BC. ∴BC为⊙O的切线．
则B︵D的长度为601·8π0·4＝43π.
课后精练
5．(2018·泰州)如图，AB 为⊙O 的直径，C 为⊙O 上一点， ∠ABC 的平分线交⊙O 于点 D，DE⊥BC 于点 E.
(1)试判断 DE 与⊙O 的位置关系，并说明理由； (2)过点 D 作 DF⊥AB 于点 F，若 BE＝3 3，DF＝3，求图中 阴影部分的面积．
∵BE＝3 3，∴BD＝ 32＋（3 3）2＝6.
∵sin∠DBF＝sin∠EBD＝36＝12，∴∠DBA＝30°.∴∠DOF＝60°.
∴sin∠DOF＝DDOF＝D3O＝ 23.∴DO＝2 3，则 FO＝ 3.
故 S 阴影＝60π×3（602
3）2－12×
3×3＝2π－3

角平分线定理专题（基础题）1. 如图，AD 是的角平分线，，垂足为F ，，和的面积分别为60和35，则的面积为A. 25B.C.D.2.如图,P 是∠AOB 平分线OC 上一点,PD ⊥OB ,垂足为D ,若PD=2,则点P 到边OA 的距离是B.2C.3.如图,△ABC 的三边AB,BC,CA 长分别是20,30,40,其三条角平分线将△ABC 分为三个三角形,则S △ABO ∶S △BCO ∶S △CAO 等于________.4．(2016·怀化)如图，OP 为∠AOB 的角平分线，PC ⊥OA ，PD ⊥OB ，垂足分别是C ，D ，则下列结论错误的是( )A ．PC ＝PDB ．∠CPD ＝∠DOPC ．∠CPO ＝∠DPOD ．OC ＝OD5．(2016·淮安)如图，在Rt △ABC 中，∠C ＝90°，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若CD ＝4，AB ＝15，则△ABD 的面积是( )A ．15B ．30C ．45D ．606．如图，△ABC 中，∠C ＝90°，AD 平分∠BAC 交BC 于点D.已知BD∶CD＝3∶2，点D 到AB 的距离是6，则BC 的长是______7．如图所示，已知△ABC 的周长是20，OB ，OC 分别平分∠ABC 和∠ACB，OD ⊥BC 于点D ，且OD ＝3，则△ABC 的面积是. ______8．如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB=m，PC=n，AB=c，AC=b，则（m+n）与（b+c）的大小关系是（）A．m+n＞b+c B．m+n＜b+c C．m+n=b+c D．无法确定角平分线性质运用（证明题）1.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：（1）2AE=AD+BE（2:）2BE=AB-AD,2、如图，四边形中，平分，于，且．求证：.3.如图，已知AC平分，于E，于F，且，求证：≌；若，，，求AC的长．角平分线的判定运用（证明题）1如图，在三角形ABC中，BP，CP分别是∠ABC，∠ACB的平分线，求证：点P在∠A的平分线上。

专题三角平分线的性质与判定一、单选题1．如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若BC=15，且BD:CD=3:2，则点D到AB的距离为（）2345．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，AB+BC+CA=18，过O作OD⊥BC于点D，且OD=3，则△ABC的面积是．6．如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE7得8910．如图，△ABC中，∠ABC，∠ACB的角平分线交于点O，过O点作MN∥BC分别交AB，AC于M，N 两点，AB=6，ΔAMN的周长是15．则AC的长为．三、解答题11．如图1，△ABC的两条外角平分线AO，BO相交于点O，∠ACB=50°．(1)直接写出∠AOB的大小；(2)如图2，连接OC交AB于K．①求∠BCK的大小；②如图3，作AF⊥OC于F，若∠BAC=105°，求证：AB=2CF．12．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，若∠ABC=60°，FD=10，求DC的长．13．如图，四边形ABCD中，∠B=90°，AB∥CD，M是BC边上的一点，且AM平分∠BAD,DM平分∠ADC,求证：(1)BM=MC；(2)AM⊥MD．14．定义：如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．(1)如图1，△ABC中，AB=AC,∠A=36°，求证：△ABC是倍角三角形；(2)如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE=AB，若AB+AC=BD，请你找出图中的倍角三角形，并进行证明．15．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，设∠ABC=α．(1)α=50°时，求∠DFC的度数；(2)证明：BE∥DF．16．在△ABC中，AO、BO分别平分∠BAC、∠ABC．(1)如图1，若∠C=32°，则∠AOB=________；(2)如图2，连结OC，求证：OC平分∠ACB；(3)如图3，若∠ABC=2∠ACB，AB=4，AC=7，求OB的长．17．如图，在△ABC中，D在BC边的延长线上，∠ACD的平分线CE交BA的延长线于点E，已知∠B=30°，∠E=40°，求证：AE=CE．18．如图，在四边形ABCD中，AB∥CD，∠C=90°，点E为BC的中点，DE平分∠CDA.(1)求证：AD=AB+CD；(2)若S△CDE=3，S△ABE=4，则四边形ABCD的面积为______.（直接写出结果）19．如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O与AB，AC分别相交于点M，N，且MN∥BC．(2)已知AB=7，AC=6，求△AMN的周长．参考答案题号12答案B B1．B【分析】本题考查的是角平分线的性质，作DE⊥AB于E，根据角平分线的性质得到CD=DE，根据题意求出CD的长即可．∵∴∵∴2∴3【详解】试题分析：本题需要分两种情况进行讨论：如图1所示：根据∠B=40°，∠C=70°可得：∠BAC=70°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=35°，则∠DAE=35°-20°=15°；如图2所示：根据∠B=40°，∠ACD=70°可得：∠BAC=30°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=15°，则∠DAE=15°+20°=35°.点睛：对于这种在三角形中求角度问题的时候，如果题目中没有给出图形，我们首先一定要根据题意画出图形，然后根据图形求出角的度数.特别要注意分类讨论的思想，在画图时一定要注意锐角三角形和钝角三角形两种情况.在画垂线的时候要注意高线在三角形内部和三角形外部两种情况.4．3：2【分析】过点D作DE⊥AB于点E，由角平分线的性质得到DE=CD，再根据三角形面积公式解答即可．【详解】解：过点D作DE⊥AB于点E，∵AD是Rt△ABC的角平分线，CD⊥AC,DE⊥AB∴DE=CDS△ABD S△ACD =12AB⋅DE12AC⋅CD=ABAC=128=32故答案为：3：2．【点睛】本题考查角平分线的性质、三角形面积公式等知识，是基础考点，掌握相关知识是解题关键．5．27【分析】作OE⊥AB于E,OF⊥AC于F，连接OA，根据角平分线的性质求出OE=OD=3和OF=OD=3，根据三角形面积公式计算即可．【详解】解：作OE⊥AB于E,OF⊥AC于F，连接OA，∵OB是∠ABC的平分线，OD⊥BC,OE⊥AB，∴OE=OD=3，同理OF=OD=3，∵AB+BC+CA=18．∴△ABC的面积=12×AB×3+12×AC×3+12×BC×3=27．故答案为：27．【点睛】本题主要考查角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．6．4【分析】根据角平分线的性质以及平行线的性质即可得出PM =PE =2，PE =PN =2，即可得出答案．【详解】解：过点P 作MN ⊥AD ，∵AD ∥BC ，∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交于点P ，PE ⊥AB 于点E ，∴AP ⊥BP ，PN ⊥BC ，∴PM =PE =2，PE =PN =2，∴MN =2+2=4．故答案为：4．7．2【分析】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，根据三角形的面积公式计算即可．【详解】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，由题意得，PE=PD=PF ， S △APC +S △APB +S △BPC =S △ACB ，∴12AC·PE+12AB·PD+12BC·PF=12AC·BC ，即12×12·PD+12×13•PD+12×5•PD=12×5×12，解得，PD=2，故答案为：2．【点睛】本题考查的是三角形的面积计算，掌握三角形的面积公式是解题的关键．8．60【分析】根据五边形的内角和求出∠BCD和∠CDE的和，再根据角平分线及三角形内角和求出∠CPD．【详解】解：∵五边形的内角和等于540°，∠A+∠B+∠E＝300°，∴∠BCD+∠CDE＝540°﹣300°＝240°，∵∠BCD、∠CDE的平分线在五边形内相交于点O，（∠BCD+∠CDE）＝120°，∴∠PDC+∠PCD＝12∴∠CPD＝180°﹣120°＝60°．故答案是：60．【点睛】本题解题的关键是知道多边形内角和定理以及角平分线的性质．9．5【分析】本题考查角平分线的性质定理，过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，利用角平分线的性质可得PF=PG=PE，然后根据三角形的面积求出PF=PE=PG=2，再利用△OMP的面积+△ONP的面积−△PMN的面积=4，进行计算即可解答．根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【详解】解：过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，∵MP平分∠AMN，NP平分∠MNB，∴PF=PG=PE，∵MN=1，△PMN的面积是1，∴ 12MN ⋅PF =1，∴PF =2，∴PG =PE =2，∵△OMN 的面积是4，∴△OMP 的面积+△ONP 的面积−△PMN 的面积=4，∴ 12OM ⋅PG +12ON ⋅PE−1=4，∴OM +ON =5．故答案为：5．10．9【分析】本题考查了等腰三角形的判定与性质，平行线的性质，根据角平分线的定义和平行线的性质可得△MOB 和△NOC 是等腰三角形，从而可得MO =MB ，NO =NC ，然后利用等量代换可得ΔAMN 的周长=AB +AC ，从而进行计算即可解答．【详解】解：∵BO 平分∠ABC ，CO 平分∠ACB ，∴∠ABO =∠OBC ，∠ACO =∠OCB ，∵MN ∥BC ，∴∠MON =∠OBC ，∠NOC =∠OCB ，∴∠ABO =∠MON ，∠ACO =∠NOC ，∴MO =MB ，NO =NC ，∵△AMN 的周长是15，∴AM +MN +AN =15，∴AM +MO +ON +AN =15∴AM +MB +NC +AN =15，∴AB +AC =15，∵AB =6，∴AC =15−6=9，故答案为：9．11．(1)65°；(2)①25°；②证明见解析．【分析】（1）根据三角形内角和定理求得∠CBA +∠CAB =130°，则∠EBA +∠BAD =230°，再由角平分线的定义求出∠OBA +∠OAB =115°，根据四边形内角和求出∠AOB 即可；（2）①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，根据角平分线的性质求解即可；②先求出KB=KC，过点A作AH∥BC交CO于点H，再求出KA=KH，则AB=CH，分别求出AH=AC，HF=CF，即可得出结论．【详解】（1）解：∵AO平分∠BAD，∴∠DAO=∠OAB，∵BO平分∠EOA，∴∠EBO=∠OBA，∵∠ACB=50°，∴∠CBA+∠CAB=130°，∴∠EBA+∠BAD=360°−130°=230°，∴∠OBA+∠OAB=115°，∴∠AOB=360°−50°−115°−130°=65°；（2）解：如图2，①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，∵AO、BO分别平分∠DAB、∠EBA，∴OM=OP，OP=ON，∴OM=ON，∴CO平分∠ACB，∵∠ACB=50°，∴∠BCK=∠ACK=25°；②证明：∵∠BAC=105°，∠ACB=50°，∴∠ABC=25°，∵∠KCB=25°，∴∠KBC=∠KCE，∴KB=KC，如图3，过点A作AH∥BC交CO于点H，∴∠AHK=∠KCB，∠HAK=∠KBC，∴∠AHK=∠HAK，∴KA=KH，∴AB=CH，∵∠AHK=∠ACH，∴AH=AC，∵AF⊥CO，∴HF=CF，∴CH=2CF，∴AB=CH=2CF．12∴∵∴∴∵∴∴故DC=5．【点睛】此题主要考查了角平分线的定义，四边形内角和定理，含30°角的直角三角形的性质等知识，解题关键是熟练掌握各性质与定理．13．(1)见详解(2)见详解【分析】（1）作NM⊥AD，根据角平分线的性质得到BM=MN,MN=CM，等量代换得到答案．（2）根据平行线的性质得到∠BAD+∠ADC=180°，根据角平分线的定义得到∠MAD+∠ADM=90°，根据垂直的定义得到答案；【详解】（1）作NM⊥AD交AD于N，∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD,∵AM平分∠BAD,DM平分∠ADC,∴BM=MN,MN=CM,∴BM=CM；（2）证明：∵AB∥CD，∴∠BAD+∠ADC=180°,∵AM平分∠BAD,DM平分∠ADC,∴2∠MAD+2∠ADM=180°,∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM⊥DM；【点睛】本题考查的是角平分线的性质，掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键．14．(1)见解析(2)△ADC和△ABC是倍角三角形，见解析【分析】（1）利用等边对等角及三角形的内角和求出∠B=∠C=72°，得到2∠A=∠C即可；（2）根据SAS证明△ABD≌△AED，得到∠ADE=∠ADB，BD=DE，证明CE=DE，得出∠C=∠BDE=2∠ADC，可得出∠ABC=2∠C．则结论得证．【详解】（1）证明：∵AB=AC，∴∠B=∠C，∵∠A+∠B+∠C=180°，∠A=36°，∴∠B=∠C=72°，∴2∠A=∠C，即△ABC是倍角三角形；（2）解：△ADC和△ABC是倍角三角形，证明如下：∵AD平分∠BAE，∴∠BAD=∠EAD，∵AB=AE，AD=AD，∴∴又∴∴∴∴∵15(2)∠EBC=∠DFC即可得出结论．【详解】（1）解：在四边形ABCD中，∠A=∠C=90°，∠ABC=α，α=50°，∴∠ADC=360°−∠A−∠C−∠ABC=130°，∵DF平分∠CDA，∠ADC=65°，∴∠FDC=12∴∠DFC =90°−65°=25°；（2）证明：在四边形ABCD 中，∠A =∠C =90°，∠ABC =α，∴∠ADC =360°−∠A−∠C−∠ABC =180°−α，∵DF 平分∠CDA ，∴∠FDC =12∠ADC =12(180°−α)，∴∠DFC =90°−12(180°−α)=12α，∵BE 平分∠ABC ，∴∠EBC =12α，∴∠EBC =∠DFC ，∴BE ∥DF ．16．(1)106°；(2)见解析；(3)3；【分析】（1）本题考查与角平分线有关的三角形内角和关系，根据∠C =32°得到∠CAB +∠CBA ，再结合角平分线求出∠CAO +∠CBO ，即可得到答案；（2）本题考查角平分线判定与性质，过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，根据角平分线性质得到OD =OF =OE ，结合角平分线的判定即可证明；（3）本题主要考查三角形全等的性质与判定，解题的关键是根据截长补短作出辅助线，在AC 上截取一点D ，使AD =AB ，连OD ，证明△ABO≌△ADO ，即可得到答案；【详解】（1）解：∵∠C =32°，∴∠CAB +∠CBA =180°−32°=148°，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴∠CAO +∠CBO =148°2=74°，∴∠AOB =180°−74°=106°；（2）证明：过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴OD =OF ，OD =OE ，∴OC 平分∠ACB ；（3）解：在AC 上截取一点D ，使AD =AB ，连OD ，设∠ACO =∠BCO =α，∵∠ABC =2∠ACB ，∴∠ABC =4α，∵BO 平分∠ABC ，∴∠ABO =∠CBO =2α，∵AO 平分∠BAC ，∴∠BAO =∠DAO ，在△ABO 与△ADO 中，AO =AO ∠BAO =∠DAO AB =AD，∴△ABO≌△ADO(SAS)，∴∠ABO =∠ADO =2α，OB =OD,AB =AD =4，又∵∠ACO =α，∴∠ACO =∠DCO =α，∴OD =OC =AC−AD =7−4=3，∴OB =3．17．证明见解析【分析】本题主要考查了角平分线的定义，三角形外角的性质以及等腰三角形的判定和三角形内角和定理的应用，根据外角的性质求出∠ECD=702，由角平分线的定义得∠ACE=∠ECD=70°，根据三角形内角和定理求出∠CAE=70°，可得∠ACE=∠CAE，从而可得结论．【详解】证明：∠B=30°，∠E=40°，∴∠ECD=∠B+∠E=70°，∵CE平分∠ACD，∴∠ACE=∠ECD=70°，在△ABE中，∠ACE+∠E+∠CAE=180°，∴∠CAE=180°−∠ACE−∠E=180°−70°−40°=70°，∴∠ACE=∠CAE，∴AE=CE．18．(1)见解析(2)14【分析】本题考查角平分线的性质，全等三角形的判定与性质．（1）过点E作EF⊥AD于F，根据角平分线的性质得出CE=EF，再证明△ABE≌△AFE，△CED≌△FED，根据全等三角形的性质得出AB=AF，DC=DF，进而得出结论；（2）由△ABE≌△AFE，△CED≌△FED，推出S△CED=S△FED，S△ABE=S△AFE，据此求解即可．【详解】（1）证明：如图，过点E作EF⊥AD于F，∵∠C=90°，AB∥CD，∴∠B=90°，∵DE平分∠CDA，∴CE=EF，∴Rt△CED≌Rt△FED(HL)，∴DC=DF，∵E是BC的中点，∴BE=CE，∴BE=EF，∵AE=AE，∴Rt△ABE≌Rt△AFE(HL)，∴AD=AF+FD=AB+CD；（2）解：∵△CED≌△FED，△ABE≌△AFE，∴S△CED=S△FED，S△ABE=S△AFE，∵S∴19(2)（（∴∴∴（∴∵∴∴∠BOM=∠ABO，∴BM=OM，同理可得：CN=ON，∴MN=OM+ON=BM+CN，∵AB=7，AC=6，∴△AMN的周长是AM+MN+AN=AM+BM+CN+AN=AB+AC=13．。

角平分线的三个定理
第一性质定理：角平分线上的点到角两边的距离相等
第一性质定理逆定理：在角的内部，到角两边距离相等的点在角的平分线上
定理：三角形内角平分线分对边所成的两条线段，与夹这个角的两边，对应成比例。

角平分线就是从一个角的顶点引出一条射线，把这个角分成两个完全相同的角。

三角形三条角平分线的交点叫做三角形的内心。

三角形的内心到三边的距离相等，是该三角形内切圆的圆心。

性质：
1.角平分线分得的两个角相等，都等于该角的一半。

（定义）
2·角平分线上的点到角的两边的距离相等。

1。

角平分线张角定理
角平分线张角定理，也称作角平分线定理，是指一个平面内的角的平分线将该角分成两个相等的张角（即角平分线将角分成两个相等的小角）。

换句话说，如果一条线段是一个角的平分线，那么它将把这个角分成两个大小相等的角。

具体表达为：
设有角AOB，角的平分线OD将其分成两个小角AOD和BOD，那么∠AOD = ∠BOD，即角AOD和角BOD是相等的。

这个定理可以用于解决各种角相关的问题，例如求角的大小、证明角的相等关系等。

通过应用角平分线定理，可以简化复杂的角度计算，将问题转化为计算两个相等的小角。

需要注意的是，角平分线定理仅适用于平面内的角，不适用于空间内的角。

此外，还有一条相关的定理是角平分线唯一定理，它表明一个给定角的平分线在平面内是唯一的，即一个角只有一条平分线。

这两个定理常常会一起使用，以解决各种关于角的问题。

专题06全等模型-角平分线模型角平分线在中考数学中都占据着重要的地位，角平分线常作为压轴题中的常考知识点，需要掌握其各类模型及相应的辅助线作法，且辅助线是大部分学生学习几何内容中的弱点，本专题就角平分线的几类全等模型作相应的总结，需学生反复掌握。

模型1.角平分线垂两边（角平分线+外垂直）【模型解读与图示】条件：如图1，OC 为AOB ∠的角平分线、CA OA ⊥于点A 时，过点C 作CA OB ⊥.结论：CA CB =、OAC ∆≌OBC ∆.图1图2常见模型1（直角三角形型）条件：如图2，在ABC ∆中，90C ∠=︒，AD 为CAB ∠的角平分线，过点D 作DE AB ⊥.结论：DC DE =、DAC ∆≌DAE ∆.（当ABC ∆是等腰直角三角形时，还有AB AC CD =+.）图3常见模型2（邻等对补型）条件：如图3，OC 是∠COB 的角平分线，AC =BC ，过点C 作CD ⊥O A 、CE ⊥OB 。

结论：①180BOA ACB ∠+∠=︒；②AD BE =；③2OA OB AD =+.例1．（2022·北京·中考真题）如图，在ABC ∆中，AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____．【答案】1【分析】作DF AC ⊥于点F ，由角平分线的性质推出1DF DE ==，再利用三角形面积公式求解即可．【详解】解：如图，作DF AC ⊥于点F ，∵AD 平分BAC ∠，DE AB ⊥，DF AC ⊥，∴1DF DE ==，∴1121122ACD S AC DF ∆=⋅=⨯⨯=．故答案为：1．【点睛】本题考查角平分线的性质，通过作辅助线求出三角形ACD 中AC 边的高是解题的关键．例2．（2022·山东泰安·中考真题）如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ，若∠BPC ＝40°，则∠CAP ＝（）A ．40°B ．45°C ．50°D ．60°【答案】C 【分析】根据外角与内角性质得出∠BAC 的度数，再利用角平分线的性质以及直角三角形全等的判定，得出∠CAP ＝∠FAP ，即可得出答案.【详解】解：延长BA ，作PN ⊥BD ，PF ⊥BA ，PM ⊥AC ，设∠PCD ＝x °，∵CP 平分∠ACD ，∴∠ACP ＝∠PCD ＝x °，PM ＝PN ，∵BP 平分∠ABC ，∴∠ABP ＝∠PBC ，PF ＝PN ，∴PF ＝PM ，∵∠BPC ＝40°，∴∠ABP ＝∠PBC ＝∠PCD ﹣∠BPC ＝（x ﹣40）°，∴∠BAC＝∠ACD﹣∠ABC＝2x°﹣（x°﹣40°）﹣（x°﹣40°）＝80°，∴∠CAF＝100°，在Rt△PFA和Rt△PMA中，{PA PA PM PF==，∴Rt△PFA≌Rt△PMA（HL），∴∠FAP＝∠PAC＝50°．故选C．【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识，根据角平分线的性质得出PM＝PN＝PF是解题的关键．例3．（2023·山东·七年级专题练习）如图，∠D＝∠C＝90°，点E是DC的中点，AE平分∠DAB，∠DEA ＝28°，求∠ABE的大小．【答案】28°【分析】过点E作EF⊥AB于F，根据角平分线上的点到角的两边距离相等可得DE=EF，根据线段中点的定义可得DE=CE，然后求出CE=EF，再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC，即可求得∠ABE的度数．【详解】如图，过点E作EF⊥AB于F，∵∠D=∠C=90°，AE平分∠DAB，∴DE=EF，∵E是DC的中点，∴DE=CE，∴CE=EF，又∵∠C=90°，∴点E在∠ABC的平分线上，∴BE平分∠ABC，又∵AD∥BC，∴∠ABC+∠BAD=180°，∴∠AEB=90°，(1)填空：角平分线的性质定理：角平分线上的点到．符号语言：∵如图1，OP 为COD ∠上的平分线，且，∴．(2)解答：已知：如图2，60AOB ∠=︒，OP 为AOB ∠的平分线，以点P 为顶点的CPD ∠与角的两边相交于点C 、D ，且120CPD ∠=︒．求证：PC PD =．(3)作图：根据以上种情况，再次寻找其它情况，点P P 为AOB ∠的平分线上的点，请你用尺规作图作PE OA ⊥于E ，作PF OB ⊥于F ，90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒，OP 平分AOB ∠，PE PF ∴=，在四边形EOFP 中，60AOB ∠=︒，90PEO PFO ∠=∠=︒，36060290120EPF ∴∠=︒-︒-⨯︒=︒，120CPD ∠=︒ ，CPD EPF ∴∠=∠，CPD EPD EPF EPD ∴∠-∠=∠-∠，CPE DPF ∴∠=∠，PEC PFD ∴≅ （ASA ）PC PD ∴=；（3）证明：如图2，作射线PC ，交OA 于C ，作PCN AOB ∠=∠，反向延长NP ，交OB 于D ，则PC PD =；,（4）解：如图3，当ODP ∠和OCP ∠互补时，PC PD =，理由如下：作PE OA ⊥于E ，作PF OB ⊥于F ，90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒，OP 平分AOB ∠，PE PF ∴=，在四边形EOFP 中，90PEO PFO ∠=∠=︒，360290180EPF AOB ∴∠+∠=︒-⨯︒=︒，180CPD AOB ∠+∠=︒ ，CPD EPF ∴∠=∠，CPD EPD EPF EPD ∴∠-∠=∠-∠，CPE DPF ∴∠=∠，PEC PFD ∴≅ (ASA)PC PD ∴=．【点睛】本题考查全等三角形的判定，角平分线的性质等知识，解决问题的关键是熟练掌握有关基础知识．模型2.角平分线垂中间（角平分线+内垂直）【模型解读与图示】条件：如图1，OC 为AOB ∠的角平分线，AB OC ⊥，结论：△AOC ≌△BOC ，OAB ∆是等腰三角形、OC 是三线合一等。

专题：平行四边形中的角平分线一、平行四边形中加一条角平分线等于一个等腰三角形例1：在平行四边形ABCD中，已知AB=5，AD=2，DE 平分∠ADC交AB于E，则BE的长度为多少？例2：在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=2，BC的长度为多少？例3：在平行四边形ABCD中，AB=4，BC=7，∠ABC 的平分线BE交AD于点E，则DE的长度为多少？例4：在平行四边形ABCD中，BC=8cm，CD=6cm，∠D=40°，BE平分∠ABC，下列结论中哪个是错误的？例5：平行四边形的一个内角的平分线与一边相交，且把这一边分成1cm和2cm两段，那么这个平行四边形的周长为多少？例6：在平行四边形ABCD中，CE平分∠BCD交AD于点E，BC=7cm，AE=3cm，则平行四边形ABCD的周长为多少？例7：在▱ABCD中，BE平分∠ABC交射线AD于点E，BC=6，DE=2，则▱ABCD的周长等于多少？二、平行四边形中加一条角平分线等于多个等腰三角形例8：在▱ABCD中，∠D=120°，∠DAB的平分线AE交DC于点E，连接BE。

若AE=AB，则∠XXX的度数为多少？三、平行四边形中加两条角平分线等于两个等腰三角形和一个直角三角形四、平行四边形中加两个等腰三角形等于两条角平分线和一个直角三角形例9：在▱ABCD中，对角线AC、BD交于点O，AE平分BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE。

下列结论哪些是正确的？例10.在平行四边形ABCD中，对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC＝60°，AB＝BC＝1，则下列结论：①∠CAD＝30°；②BD＝√3；③S▱ABCD＝AB·AC；④OP＝DO；⑤S△APO＝S△BPO，正确的有①、②、③、⑤。

【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）素养拓展17解三角形中三角形的中线和角平分线问题（精讲+精练）一、三角形中线问题如图在ABC ∆中，D 为CB 的中点，2AD AC AB =+，然后再两边平方，转化成数量关系求解！（常用）二、角平分线问题如图，在ABC ∆中，AD 平分BAC ∠，角A ,B ,C 所对的边分别为a ，b ，c ①等面积法ABC ABD ADCS S S ∆∆∆=+⇒111sin sin sin 22222A AAB AC A AB AD AC AD ⨯⨯=⨯⨯+⨯⨯（常用）②内角平分线定理：AB AC BD DC =或AB BD AC DC =③边与面积的比值：ABDADCS AB AC S = 【典例1】在ABC 中，内角,,A B C 的对边分别为,,a b c ，2,2sin 3sin2c b A C ==.(1)求sin C ；(2)若ABC 2，求AB 边上的中线CD 的长.【分析】（1）利用二倍角公式，结合正弦定理、余弦定理及同角三角函数关系式即可求出结果；（2）利用三角形面积公式，及（1）的相关结论，再结合平面向量的四边形法则，利用向量的线性表示出CD，最后利用求模公式即可求AB 边上的中线CD 的长.【详解】（1）因为2sin 3sin2A C =，所以2sin 6sin cos A C C =，二、题型精讲精练一、知识点梳理【典例2】在ABC 中.AB ＝2，AC ＝，BC ＝4，D 为AC 上一点.(1)若BD 为AC 边上的中线，求BD ；(2)若BD 为∠ABC 的角平分线，求BD .【题型训练-刷模拟】1.中线问题一、解答题2.角平分线问题一、解答题1．（2023·辽宁葫芦岛·统考一模）在ABC 中，角,,A B C 所对的边分别为,,a b c ．()()()sin sin sin A B A B A C -=+-+，角A 的角平分线交BC 于点D ，且3b =，6c =．(1)求角A 的大小；(2)求线段AD 的长．【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）素养拓展17解三角形中三角形的中线和角平分线问题（精讲+精练）一、三角形中线问题如图在ABC ∆中，D 为CB 的中点，2AD AC AB =+，然后再两边平方，转化成数量关系求解！（常用）二、角平分线问题如图，在ABC ∆中，AD 平分BAC ∠，角A ,B ,C 所对的边分别为a ，b ，c ①等面积法ABC ABD ADCS S S ∆∆∆=+⇒111sin sin sin 22222A AAB AC A AB AD AC AD ⨯⨯=⨯⨯+⨯⨯（常用）②内角平分线定理：AB AC BD DC =或AB BD AC DC =③边与面积的比值：ABDADCS AB AC S = 【典例1】在ABC 中，内角,,A B C 的对边分别为,,a b c ，2,2sin 3sin2c b A C ==.(1)求sin C ；(2)若ABC 2，求AB 边上的中线CD 的长.【分析】（1）利用二倍角公式，结合正弦定理、余弦定理及同角三角函数关系式即可求出结果；（2）利用三角形面积公式，及（1）的相关结论，再结合平面向量的四边形法则，利用向量的线性表示出CD，最后利用求模公式即可求AB 边上的中线CD 的长.【详解】（1）因为2sin 3sin2A C =，所以2sin 6sin cos A C C =，二、题型精讲精练一、知识点梳理【典例2】在ABC 中.AB ＝2，AC ＝，BC ＝4，D 为AC 上一点.(1)若BD 为AC 边上的中线，求BD ；(2)若BD 为∠ABC 的角平分线，求BD .【题型训练-刷模拟】1.中线问题一、解答题设AC BC x ==，则2xCM =，由余弦定理可得22224x AM x =+-所以2x =，故122S =⨯⨯⨯22cos 2CD AD ADC CD AD ∠+-=⋅）;）.）首先根据正弦定理，将原等式中的边化为角，再利用两角和的正弦公式化简，求出,，得到，最后代入面积公式）由,得，根据上一问的结果可求，再根据中线表示向量为，两边平方后得到结果）,由正弦定理可化为：,,即,,,又,得,,即，的面积）由,得，，又，解得：，又,,,即边上的中线的长为.17．（2023·全国·高三专题练习）在(1)求角A 的大小(2)若BC 边上的中线由（1）知222b a bc c =--，即2b 在ABD △中，由余弦定理得：2c 在ADC △中，由余弦定理得：2b2.角平分线问题一、解答题3）63=，ABCπsin63bc=，3=，24）由第（1）问知，2π3ACB ∠=，若CD 如图，设ABC ，ACD ，BCD △的面积分别为由132AM BC ==，可得2A π=，∴22236b c a +==，2365b =，所以221136·2225S bc b b ====．②法一：由CD CB λ=，得又(1)=-=- CE AE AC AB λ所以[(1⋅=+- AD CE AB λλ12．（2023·广东深圳·深圳中学校联考模拟预测）(1)求角B ；(2)设ABC ∠的角平分线【答案】(1)2π3根据三角形面积公式可得1 2等式两边同除以12ab CD⋅可得。

专题19 角平分线定理在圆锥曲线中的应用微点2 角平分线定理在圆锥曲线中的应用综合训练
(1)求截口BAC 所在椭圆C 的方程；
(2)点P 为椭圆C 上除长轴端点和短轴端点外的任意一点．
①是否存在m ，使得P 到2F 和P 到直线值，如果不存在，请说明理由；
②若12F PF ∠的角平分线PQ 交y 轴于点斜率分别为1k ，2k ，请问k k
k k +是否为定值，若是，求出这个定值，若不是，请说明
（1）求椭圆C 的方程；
（2）如图，若斜率为(0)k k ≠点的左侧)且121RF F PF Q ∠=∠15．椭圆C ：221x y +=(a >b
参考答案：
3．B
【分析】在1PF Q △中，利用角平分线性质定理可推出2PF Q △中，根据角平分线性质定理【详解】解：因为I 为12PF F △的内心，所以
【点睛】本题主要考查了椭圆的定义及标准方程，以及圆的方程、合应用，着重考查推理论证能力及运算求解能力，属于难题。

高中数学-角平分线相关定理模块一 张角定理如图，在ABC △中，D 为BC 边上的一点，连接AD ，设AD l ，BAD α∠=，CAD β∠=，则一定有sin+sin sin=l bc．证明：ABC ABDACD S S S △△△，()111sin sin sin 222bc cl bl αβαβ∴+=+，同除以12bcl 得：sin +sin sin=lbc． 【例1】在中ABC △，角A ，B ，C 所对的边分别为a ，b ，c ，120ABC ∠=︒，BD BC ⊥交AC 于点D ，且1BD =，则2a c +的最小值为 ．【例2】如图， 在ABC △中， 已知点D 在BC 边上，AD AC ⊥，sin BAC ∠，AB =3AD =，则CD 的长为 ．【例3】ABC △中，D 是BC 上的点，AD 平分BAC ∠，ABD △面积是ADC △面积的2倍． （1）求sin sin BC；（2）若1AD =，DC ，求BD 和AC 的长． 模块二：角平分线张角定理根据张角定理：①当时，1cos2AD ADb c（角平分线张角定理） ②21()sin tan 2ABCS AD b c AD △（角平分线面积问题）证明：①根据张角定理可得：sin 2sinsin=AD b c ，2sin cos sinsin=AD b c，1cos2AD ADb c ②2111112sinsin 2()sin =()sin sin222sin 2S Sbc bc AD AD b c AD bc ADbctan AD S ，αtan 2AD S ≥∴，当仅当c b =时等号成立.【例4】如图，在ABC △中， 角A ，B ，C 所对的边分别为a ，b ，c ，cos b C a =，点M 在线段AB 上， 且ACM BCM ∠=∠． 若66b CM ==，则cos BCM ∠=（ ）A B ．34C D【例5】在ABC △中，角A ，B ，C 所对的边分别为a ，b ，c ，23ABC π∠=，ABC ∠的平分线交AC 于点D ，1BD =，则a c +的最小值为 ． 【例6】在ABC △中，内角A ，B ，C 对的边分别为a ，b ，c ，23ABC π∠=，BD 平分ABC ∠交AC 于点D ，2BD =，则ABC △的面积的最小值为（ ）A ．B ．C ．D ．模块三：角平分线之斯库顿定理如图，AD 是ABC △的角平分线，则2··.AD AB AC BD CD =-就其位置关系而言，可记忆：中方=上积一下积.已知：在ABC △中，2··AD BD DC AB AC +=中，AD 是BAC ∠的平分线，求证： 2··AD BD DC AB AC +=【证明】作的外接圆，延长AD 交圆于E ，连BE ，如图12E C ABE ADC ∠=∠∠=∠∴∽△△、 ·AB AEAD AC∴=即··AD AE AB AC =··AD AD DE AB AC ∴+=（）2··AD AD DE AB AC ∴=+ 由相交弦定理得：2····BD DC AD DE AD BD DC AB AC =∴+=，注意：角平分线张角定理强调的是角度，斯库顿定理强调的是长度，斯库顿定理可以绕过求张角而直接求出三角形的各边长，通常和内角平分线定理合在一起出考题.【例7】在ABC △中，5AB =，7AC =，6BC =，A ∠的平分线AD 交边BC 于点D ，则AD = ．【例8】如图，在ABC △中，2C B ∠=∠，3AC =，5BC =，求AB 之长.模块四：角平分线之倍角定理222222b a a c B Ac b b a C B a c c b A C=+⇔==+⇔==+⇔=（）（）（），这样的三角形称为“倍角三角形”.【例9】在ABC △中，内角A ，B ，C 所对的边分别是a ，b ，c ．已知8=5b c ，=2C B ，则cos =C （ ）A ．725B ．725-C ．725±D ．2425【例10】设锐角ABC △的三个内角A ，B ，C 的对边分别为a ，b ，c ，且1c =，2A C =，则ABC △周长的取值范围为（ ） A．(0,2+ B．(0,3C．(2+3+D．(2+3【例11】在ABC △中，角A 、B 、C 对边分别为a 、b 、c ，若22a b bc =+，且(60,90)A ∈︒︒，则ab取值范围是 ．【例12】如图，四边形ABCD 中，CE 平分ACD ∠，AE CE ==，DE =，若ABC ACD ∠=∠，则四边形ABCD 周长的最大值为（ ）A ．24B ．12+C．D ．3(5课后练习1．已知ABC △的边AB ，AC 的长分别为2，3，120BAC ∠=︒，则BAC ∠的角平分线AD 的长为（ ）A B ．35C D ．652．已知AB BD ⊥，30A ∠=︒，45C ∠=︒，CD =sin CBD ∠=，则AB 的值为（ ）AB C D3．在ABC △中，内角A ，B ，C 所对应的边分别为a ，b ，c ，60ABC ∠=︒，ABC ∠的平分线交AC 于点D ，且BD =2a c +的最小值为（ ） A．4B ．5C ．2+D ．3+4.在ABC △中，角A ，B ，C 所对的边分别为a ，b ，C ，120ABC ∠=︒，ABC ∠的平分线交AC 于点D ，且2BD =，则4a c +的最小值为 ．5.已知ABC △的面积为S ，2BAC α∠=，AD 是ABC △的角平分线，则AD 长度的最大值为（ ）A sin S αBC tan S αD6.在ABC △中，120BAC ∠=︒，AD 为BAC ∠的平分线，2AB AC =，则（ ） A ．2AB AD =B ．3AB AD =C ．2AB AD =或3AB AD =D ．5AB AD =7.设ABC △的内角A ，BC 的对边分别为a ，b ，c ，且6b =，4c =，2A B =，则a = ．8.在ABC △中，若a =，2A B =，则cos B 等于（ ）A B C D 9.在斜ABC △中，设角A ，B ，C 的对边分别为a ，b ，c ，已知sin a sin sinC A b B c +- 4sin cos b B C =，CD 是角C 的角平分线，且CD b =，则cos C =（ ）A ．34 B ．18C ．23D ．1610.在ABC △中，2AB AC =，内角A 的平分线与BC 交于D ，且AC tAD =，则t 的取值范围是（ ） A ．3(0,)4B ．3(4，1)C ．4(1,)3D ．3(4，)+∞11.已知ABC △中，角A ，B ，C 对应的边分别为a ，b ，c ，AD 平分BAC ∠与BC 边交于D 点，若7a =，5b =，3c =，则线段AD 的长为（ ）A ．258B ．218C ．158 D ．9812.如图，在ABC △中，90C ∠=︒，内角A 的平分线AD 的长为7，且7sin 18B =，则cos CAD ∠= ；AB 的长是 ．13.在ABC △中，角A ，B ，C 所对的边分别为a ，b ，c ，若ABC △为锐角三角形，且满足22b a ac -=，则11tan tan A B-的取值范围是（ ）A ．B ．C ．D ．(1,)+∞14．在锐角ABC △中，2A B ∠=∠，B ∠、C ∠的对边长分别是b 、c ，则bb c+的取值范围是（ ） A ．11(,)43B ．11(,)32C ．12(,)23D ．23(,)3415.如图，在ABC △中，AB AC >，BC =，60A =︒，ABC △的面积等于，则sin B = ，角平分线AM 的长等于 ．16.在ABC △中，若:1:2A B ∠∠=，且ACB ∠的平分线CD 把ABC △分成面积比为5:3的两部分，则cos A = ．17．如图，在ABC △中，sin sin BD B CD C ⋅=⋅，2BD DC ==2AD =，则ABC △的面积为（ ）AB C ．D ．18．在ABC △中，角A 的平分线交BC 于点D ，22BD CD ==，则ABC △面积最大值为 ．19.已知在ABC △中，内角A ，B ，C 所对的边分别为a ，b ，c ，且满足2cos a a B c +=． （1）求证：2B A =；（2）若ABC △为锐角三角形，且2c =，求a 的取值范围．20．在ABC △中，a ，b ，c 分别是A ∠，B ∠，C ∠的对边，已知a =． （1）若2A B ∠=∠，求cos B ；（2）若2AC =，求ABC △面积的最大值．。