欧姆定律及串并联特点

欧姆定律是电学领域中最基本的定律之一，描述了电流、电压和电阻之间的关系。

欧姆定律的数学表达式为V=IR，其中V代表电压，I代表电流，R代表电阻。

欧姆定律在电路分析中起着重要的作用，特别是在串并联电路中。

本文将详细介绍欧姆定律在串并联电路中的应用。

一、欧姆定律在串联电路中的应用串联电路是指电路中的各个电阻依次连接，电流在各个电阻中依次流过。

在串联电路中，各电阻的电流相等，总电压等于各电阻电压之和。

1.电流相等在串联电路中，由于电流只有一条路径可走，因此电流在各个电阻中是相等的。

根据欧姆定律，I=V/R，可以得到各电阻的电流相等，即I1=I2==In。

2.总电压等于各电阻电压之和V=IR，可以得到各电阻的电压为V1=IR1，V2=IR2，，Vn=IRn。

因此，总电压Vtotal=V1+V2++Vn=I(R1+R2++Rn)。

3.电阻等效在串联电路中，可以将多个电阻看作一个等效电阻。

等效电阻的阻值等于各电阻阻值之和，即Req=R1+R2++Rn。

根据欧姆定律，总电流I=Vtotal/Req。

二、欧姆定律在并联电路中的应用并联电路是指电路中的各个电阻分别连接在电压相同的节点上，电流在各个电阻中分流。

在并联电路中，各电阻的电压相等，总电流等于各电阻电流之和。

1.电压相等在并联电路中，由于各个电阻连接在电压相同的节点上，因此各电阻的电压相等。

根据欧姆定律，V=IR，可以得到各电阻的电压相等，即V1=V2==Vn。

2.总电流等于各电阻电流之和I=V/R，可以得到各电阻的电流为I1=V/R1，I2=V/R2，，In=V/Rn。

因此，总电流Itotal=I1+I2++In=V(1/R1+1/R2++1/Rn)。

3.电阻等效在并联电路中，可以将多个电阻看作一个等效电阻。

等效电阻的倒数等于各电阻倒数之和，即1/Req=1/R1+1/R2++1/Rn。

根据欧姆定律，总电流Itotal=V/Req。

总结：欧姆定律在串并联电路中的应用是电路分析的基础。

欧姆定律及电路中电流的串并联一、欧姆定律1.定义：欧姆定律是指导体中的电流与两端电压成正比，与导体的电阻成反比。

2.公式：I = U / R，其中I表示电流，U表示电压，R表示电阻。

3.适用范围：欧姆定律适用于纯电阻电路，即电路中只有电阻、电源和导线。

4.影响因素：电流的大小受电压和电阻的影响，当电压增大或电阻减小时，电流增大；当电压减小或电阻增大时，电流减小。

二、电路中电流的串并联1.串联电路：串联电路是指电路中电流只有一条路径，各用电器相互影响。

2.并联电路：并联电路是指电路中电流有多条路径，各用电器互不影响。

3.串并联混合电路：串并联混合电路是指电路中既有串联部分，又有并联部分。

4.串并联规律：a)串联电路的总电阻等于各分电阻之和，即R = R1 + R2 + … +Rn。

b)并联电路的总电阻的倒数等于各分电阻倒数之和，即1/R =1/R1 + 1/R2 + … + 1/Rn。

5.电压和电流分配规律：a)在串联电路中，各用电器的电压之和等于电源电压。

b)在并联电路中，各用电器的电压相等，等于电源电压。

c)在串联电路中，各用电器的电流相等。

d)在并联电路中，各用电器的电流之和等于总电流。

6.功率计算：a)串联电路的总功率P = UI，其中U为电源电压，I为总电流。

b)并联电路的总功率P = UI，其中U为电源电压，I为总电流。

7.欧姆定律是电路学中的基本定律，掌握欧姆定律对于理解电路的运行原理至关重要。

8.电路中的电流串并联现象是实际应用中常见的，了解串并联规律有助于分析和解决实际问题。

9.电路中的电压、电流和功率计算是电路分析的重要内容，掌握这些计算方法可以更好地理解电路的性能。

习题及方法：1.习题：一个电阻为20Ω的电阻器，通过它的电流为0.5A，求电阻器两端的电压。

方法：根据欧姆定律，电压U等于电流I乘以电阻R，即U = I * R。

将给定的数值代入公式，得到U = 0.5A * 20Ω = 10V。

我们来探讨串并联电路中电流、电压和电阻的规律公式。

在电路中，串联电路指多个电器依次连接在一条路上，而并联电路指多个电器并排连接在电源的两端。

这两种电路中电流、电压和电阻的规律公式有着明显的区别，接下来我们将分别进行探讨。

1. 串联电路中的规律公式：在串联电路中，电流沿着唯一一条路径流动，因此多个电器的电流大小相等。

根据欧姆定律，串联电路中的总电阻等于各个电器电阻的总和，即R总 = R1 + R2 + ... + Rn。

而总电压等于各个电器电压之和，即U总 = U1 + U2 + ... + Un。

根据欧姆定律，电流I总等于总电压U总除以总电阻R总，即I总 =U总 / R总。

串联电路中电流、电压和电阻的规律公式为：I总 = U总 / (R1 + R2+ ... + Rn)。

2. 并联电路中的规律公式：在并联电路中，电压相同，而电流则分流经过各个电器，因此多个电器的电压大小相等。

根据欧姆定律，并联电路中的总电导等于各个电器电导的总和的倒数，即G总 = G1 + G2 + ... + Gn。

而总电流等于各个电器电流之和，即I总 = I1 + I2 + ... + In。

根据欧姆定律，总电导G总等于总电流I总除以总电压U总，即G总= I总 / U总。

并联电路中电流、电压和电阻的规律公式为：I总 = U总 * (G1 + G2 + ... + Gn)。

从上面的分析可以看出，串联电路和并联电路中电流、电压和电阻的规律公式有着明显的区别。

在实际应用中，我们可以根据具体情况选择合适的电路连接方式来满足需求。

对于工程师和电子爱好者来说，深入理解电路中电流、电压和电阻的规律公式对于设计和维护电路至关重要。

总结回顾一下，串并联电路中的电流、电压和电阻的规律公式分别为：串联电路：I总 = U总 / (R1 + R2 + ... + Rn)；并联电路：I总 = U总 * (G1 + G2 + ... + Gn)。

个人观点：对于电路中的电流、电压和电阻规律，我认为深入理解和掌握这些规律公式，有助于我们更好地应用于实际工程中。

欧姆定律在串并联电路中的应用
欧姆定律是电学中最基本的定律之一，它描述了电流、电压、电阻之间的关系。

在串并联电路中，欧姆定律有很大的应用。

在串联电路中，所有电流的大小相同，而电压随电阻大小的变化而变化，根据欧姆定律可以得到：
总电阻= R1 + R2 + R3 + ... + Rn
总电压= V1 + V2 + V3 + ... + Vn
电流= 总电压/ 总电阻
在并联电路中，所有电压的大小相同，而电流随电阻大小的变化而变化，根据欧姆定律可以得到：
总电流= I1 + I2 + I3 + ... + In
总电阻= (1/R1 + 1/R2 + 1/R3 + ... + 1/Rn)^-1
总电压= I * 总电阻
因此，在串并联电路中，欧姆定律可以帮助我们计算电阻、电流和电压之间的关系，方便我们设计和调整电路。

欧姆定律是电学中一个重要的基本定律，描述了电压、电流和阻抗之间的关系。

而串联和并联规律则是指在电路中电阻或其他负载组合的方式。

下面是关于欧姆定律、串联规律和并联规律的总结：
1. 欧姆定律（Ohm's Law）：欧姆定律表明电路中的电流（I）与电压（V）和电阻（R）之间存在线性关系。

根据欧姆定律，电流（I）等于电压（V）与电阻（R）的比值，即I = V/R。

这意味着，当电压保持不变时，电流随着电阻的增加而减小；当电阻保持不变时，电流随着电压的增加而增加。

2. 串联规律：在电路中，当多个电阻或负载连接在一起形成串联连接时，它们依次连接在一起，形成一个电流沿着这些负载依次流动的电路。

根据串联规律，串联电阻的总电阻等于各个电阻之和，即Rt = R1 + R2 + R3 + ...。

而串联电路中的电流保持不变，即各个电阻上的电流相等。

3. 并联规律：在电路中，当多个电阻或负载并联连接时，它们连接在相同的电源线上，分别形成一个平行的分支电路。

根据并联规律，并联电阻的总电阻等于各个电阻的倒数之和的倒数，即1/Rt = 1/R1 + 1/R2 + 1/R3 + ...。

而并联电路中的电压保持不变，即各个电阻上的电压相等。

这些定律和规律为电路分析、设计和故障排除提供了重要的基础，使我们能够更好地理解和计算电路中的电压、电流和电阻之间的关系。

1．请你利用欧姆定律和串联的电流与电压的特点推导出串联电路总电阻与各串联导体电阻的关系（R 总=R 1+R 2）。

2．串联电路的总电阻等于 ，写成数学表达式是 ；串联电路中的电流特点是 ，写成数学表达式是 ；串联电路的电压特点是 ，写成数学表达式是 ．3．几个导体串联起来总电阻比其中任何一个导体的电阻都 ，因为导体的串联相当于增加了导体的 ． 4．阻值为10Ω的电阻R 1与阻值为25Ω的电阻R 2串联后的总电阻是 ．若通过R 1的电流为0．2A ，则通过电阻R 2的电流是 ，R 2两端的电压是 ． 5．R 1与R 2串联后的总电阻为350Ω，已知电阻R 1=170Ω，则电阻R 2= Ω． 6． R 1=5Ω，R 2=10Ω，串联后接到6V 的电源上，则R 1两端的电U 1为 ，R 2两端的电压U 2为 ，U 1∶U 2= ．7．电阻R 1、R 2串联在电路中，已知R 1∶R 2=3∶2，则通过两电阻的电流之比I 1∶I 2= ，电阻两端的电压之比U 1∶U 2= ．8．将电阻R 1、R 2串联在电路中，已知：R 1=3R 2，总电压为4V ，则R 1两端的电压为 （ ）． A ．4V B ．3V C ．2V D ．1V9．如图5所示当滑动变阻器的滑片自左向右移动的过程中，电路的总电阻、电流表示数和电压表示数的变化情况分别是（ ）． A ．变小、变大、不变 B ．不变、变大、变小 C ．变大、变小、变小 D ．变大、变大、变大10．如图2所示，电流表的示数是0．3A ，灯泡L 的电阻为3Ω， 电压表示数为9V ，那么，此时变阻器接入电路的电阻是多少。

（试用两种方法求解）11．如图7，R 1=10Ω，R 2是阻值为0～40Ω的变阻器，电源电压为12V ．当P 在B 端时，电压表的示数多大？当P 在AB 中点时，电流表、电压表的示数各多大？图4图2图7图51．并联电路的电流特点是，写成数学表达式是；串联电路的电压特点是，写成数学表达式是．2．导体并联后相当于增加导体的，因此，几个导体并联后总电阻比其中任何一个导体的电阻都要．3．一根粗细均匀的电阻线，阻值为R，将其用拉丝机均匀拉长为原来的2倍，再将其对折，则它的电阻值 R．（填“＞”，“＜”或“=”）4．并联电路，随着并联支路数目增加，其总电阻将（）．A．变大 B．变小 C．不变 D．无法判断5．如图2：R1=10Ω，R2=20Ω，S断开时，电流表的示数为0．6A．则电源电压是，S闭合后电流表的示数为．6．如图5所示的电路，电流表A1与电流表A2的读数之比是5:2，则两个电阻R1与R2之比是（）． A．2:5 B．5:2 C．3:2 D．2:37．如图2所示的电路中，电流表的读数：A1为0．12A，A2为0．08A，A3为0．1A，电压表的示数为2．8V．由此可知干路中的电流是 A；灯L1两端的电压为 V，灯L2两端的电压为 V．8．R1=5Ω，R2=10Ω，并联后接到6V的电源上，则R1和R2中电流之比I1∶I2= ．则R1和R2两端电压之比U1∶U2= ．9．将电阻R1、R2并联在电路中，已知：R1=3R2，干路电流为0.4A,，则R1、R2电流分别为I1 = ；I2= 。

结合欧姆定律对串并联电路中的电流、电压及电阻的特点分析作者：华年晓月一、结合欧姆定律：Ｉ＝ＵＲ 可以对串、并联电路中电流、电压及电阻的相互关系进行如下分析：串联：电流： Ｉ ＝Ｉ ＝ Ｉ Ｉ/ ＝Ｉ1 + Ｉ２ 电压： Ｕ ＝ Ｕ１ + Ｕ2 Ｕ１ ＝ Ｕ2 电阻： Ｒ ＝ Ｒ１ + Ｒ2１Ｒ＝１Ｒ +１Ｒ Ｒ=Ｒ Ｒ Ｒ Ｒ 分压作用： ＵＵ ＝ Ｒ Ｒ 分流作用： Ｉ Ｉ ＝ Ｒ Ｒ二、串、并联电路中电阻的分析：１、为什么分析电阻：因为动态电路的变化过程中，引起电路中各用电器电流、电压、电功率变化的根本原因是连入电路中电阻的变化（电源电压不变时）。

只有先分析出电路中电阻的变化情况，才能准确的分析各部分（或各支路）电路中的电流、电压的变化情况；从而进一步分析电路中各仪表的示数变化情况或仪表的示数比值变化情况。

还可分析各用电器消耗的功率变化情况、在相同时间内电流所做的功（或产生的热量）变化情况等各种电路的变化问题。

只有能够准确的分析电路中电阻的变化情况才能有效的得出其它物理量的变化情况，如果电路变化中电阻的大、小变化情况分析错Ｉ误，将会直接影响整个电路变化情况的判断。

２、串联、并联电阻变化情况的不同点（１）几个电阻串联相当于增大了导体的长度；几个电阻并联相当于增大了导体的横截面积。

（２）串联电路中的总电阻比其中任何一个串联的电阻都大；并联电路中的总电阻比其中任何一个并联的电阻都小。

（３）要用几个小电阻组成一个大电阻的方法是将其串联；要用几个大电阻组成一个小电阻的方法是将其并联。

（４）n个阻值相同的电阻串联后的总电阻：Ｒ总＝nＲ；２个阻值相同的电阻串联后的总电阻是其中一个的2倍。

n个阻值相同的电阻并联后的总电阻：Ｒ总＝Ｒ2个阻值相同的电阻并联后的总电阻是其中一个的（５）２个阻值相同的电阻先串联后的总电阻Ｒ串与它们并联后的总电阻Ｒ并的比值为：Ｒ串∶Ｒ并＝4∶1。

（６）串联的电路中当电阻数量增多时，其总电阻将会变大；（数量减少时其Ｒ总将会变小）。

串并联电路特点总结
串联电路特点：
1.在串联电路中，电流在电路中的各个元件中是相同的，由于电流只有一条路径可走，所以电流在整个电路中保持不变。

2.串联电路中，电压在电路中的各个元件中之和等于总电压，即电压的分配取决于各个元件的电阻和电流值。

根据欧姆定律可以得知，电压与电流成正比，所以电压在电阻值较大的元件上会分配更多。

3.串联电路中，电功率的总和等于各个元件的电功率之和。

电功率等于电阻乘以电流的平方，所以电阻值较大的元件会消耗更多的能量。

4.串联电路中，若其中一个元件断开，则电路中的整个电流会中断，其他元件都无法正常工作。

并联电路特点：
1.在并联电路中，电压在电路中的各个元件中是相同的，由于电压在各个元件之间有多个路径可选，所以电压在整个电路中保持不变。

2.并联电路中，电流在电路中的各个元件中之和等于总电流，即电流的分配取决于各个元件的电阻和电压值。

根据欧姆定律可以得知，电流与电阻成反比，所以电流在电阻值较小的元件上会分配更多。

3.并联电路中，电功率的总和等于各个元件的电功率之和。

电功率等于电压乘以电流，所以电压值较大的元件会消耗更多的能量。

4.并联电路中，若其中一个元件断开，则电路中的总电流不受影响，其他元件仍然可以正常工作。

综上所述，串联电路和并联电路有着各自的特点和应用场景。

串联电路适合用于需要保持电流稳定的情况，如在灯泡等需要稳定亮度的设备中使用；而并联电路适合用于需要保持电压稳定的情况，如在家庭用电中各个电器的并联使用。

在实际应用中，可以根据不同的需求选择串联电路或并联电路，以达到最佳的电路效果。

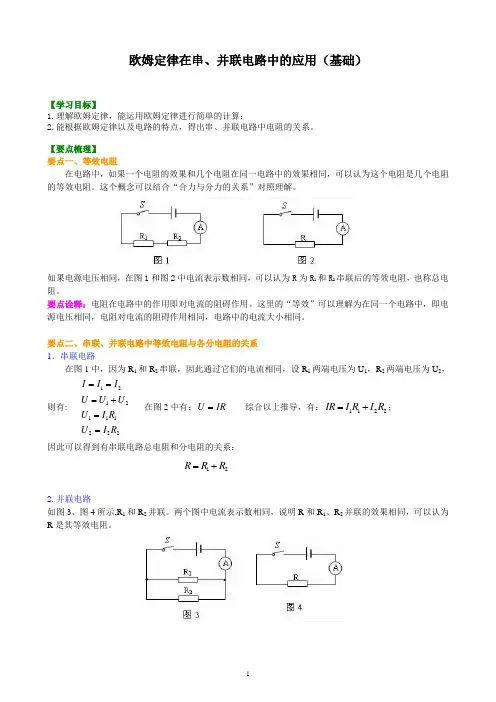
欧姆定律在串、并联电路中的应用（基础）【学习目标】1.理解欧姆定律，能运用欧姆定律进行简单的计算；2.能根据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

【要点梳理】要点一、等效电阻在电路中，如果一个电阻的效果和几个电阻在同一电路中的效果相同，可以认为这个电阻是几个电阻的等效电阻。

这个概念可以结合“合力与分力的关系”对照理解。

如果电源电压相同，在图1和图2中电流表示数相同，可以认为R 为R 1和R 2串联后的等效电阻，也称总电阻。

要点诠释：电阻在电路中的作用即对电流的阻碍作用。

这里的“等效”可以理解为在同一个电路中，即电源电压相同，电阻对电流的阻碍作用相同，电路中的电流大小相同。

要点二、串联、并联电路中等效电阻与各分电阻的关系1．串联电路在图1中，因为R 1和R 2串联，因此通过它们的电流相同，设R 1两端电压为U 1，R 2两端电压为U 2，则有: 1212111222I I I U U U U I R U I R ===+== 在图2中有：U IR = 综合以上推导，有：1122IR I R I R =+；因此可以得到有串联电路总电阻和分电阻的关系：12R R R =+2.并联电路如图3、图4所示,R 1和R 2并联。

两个图中电流表示数相同，说明R 和R 1、R 2并联的效果相同，可以认为R 是其等效电阻。

在图3中，有 1212111222=I I I U U U U I R U I R =+===在图4中，有:U I R = 综合以上推导，有1212U U U R R R =+; 即：12111R R R =+ , 1212R R R R R =+要点诠释：（1）导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即12......n R R R R =+++。

（2）如果用n 个阻值均为R 0的导体串联，则总电阻为0R nR =。