线性与对数模型案例分析
- 格式:doc
- 大小:459.50 KB
- 文档页数:11
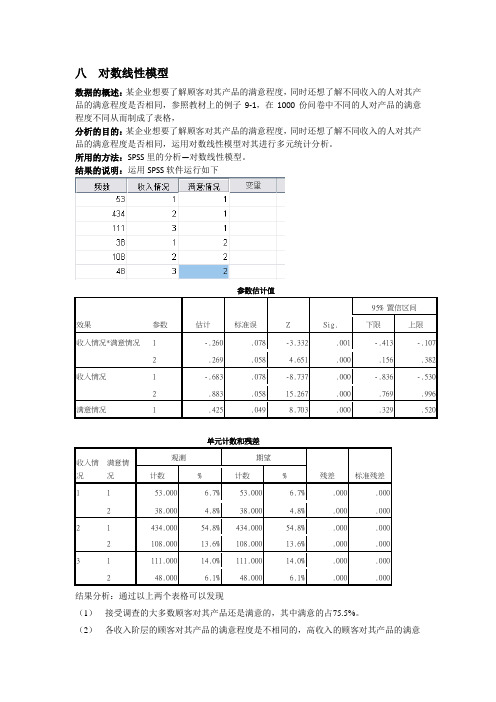
八对数线性模型
数据的概述:某企业想要了解顾客对其产品的满意程度,同时还想了解不同收入的人对其产品的满意程度是否相同,参照教材上的例子9-1,在1000份问卷中不同的人对产品的满意程度不同从而制成了表格,
分析的目的:某企业想要了解顾客对其产品的满意程度,同时还想了解不同收入的人对其产品的满意程度是否相同,运用对数线性模型对其进行多元统计分析。
所用的方法:SPSS里的分析—对数线性模型。
结果的说明:运用SPSS软件运行如下
结果分析:通过以上两个表格可以发现
(1)接受调查的大多数顾客对其产品还是满意的,其中满意的占75.5%。
(2)各收入阶层的顾客对其产品的满意程度是不相同的,高收入的顾客对其产品的满意
度最低(占6.7%),而中等收入的对其满意度最高(占54.8%)。

实验报告——线性模型与对数模型举例分析一、实验目的本实验的目的在于研究GNP 与货币是否有关系,若有关系有怎样的数量关系,用哪种模型来描述二者之间关系较为合适。
二、下面根据GNP/货币供给数据,得到的回归结果(Y=GNP ,X=货币供给):年 GNP (10亿美元) Μ2 年 GNP (10亿美元) Μ2 1973 1359.3 861.0 1981 3052.6 1795.5 1974 1472.8 908.5 1982 3166.0 1954.0 1975 1598.4 1023.2 1983 3405.7 2185.2 1976 1782.8 1163.7 1984 3772.2 2363.6 1977 1990.5 1286.7 1985 4014.9 2562.6 1978 2249.7 1389.0 1986 4240.3 2807.7 1979 2508.2 1500.2 1987 4526.7 2901.0 1980 2732.0 1633.1 平均值 2791.47 1755.70模型 截距 斜率2r双对数 0.5531 0.9882 0.9926t=(3.1652) 41.889 对数-线性 6.8616 0.00057 0.9493 (增长模型) t=(100.05) 15.597 线性-对数 -16329.0 2584.8 0.9832t=(-23.494) 27.549 线性 101.20 1.5323 0.9915 (LIV 模型) t=(1.369) 38.867a. 解释每个模型斜率的意义。
1. 双对数模型中斜率0.9882表示,货币供给每提高1个百分点,GNP 平均增加约0.98个百分点。
2. 对数―线性模型中的斜率0.00057表示,货币供给每增加1(10亿)美元,GNP 将以0.057%的速度增长。
3. 线性―对数模型中的斜率2584.8表示,货币供给每提高1个百分点,GNP 将增加25.848(10亿)美元。

第5章列联表分析与对数线性模型实验5-1 列联表分析一、列联表若总体中的个体可按两个属性A与B分类,A有r个等级,B有c个等级,从总体中抽取大小为N的样本,每种属性的样本数如下表所示:称上表为r×c列联表。
当r=2=c时,称上表为2×2列联表或四格表。
本节仅涉及四格表检验。
例1 对肺癌患者和对照组的调查结果:问是否患肺癌与是否吸烟独立与否?例2 1976年至1977年美国佛罗里达州29个区的凶杀案件中凶手的肤色和是否被判死刑的326个犯人的情况如下,问是否存在种族歧视与审判不公?二、实验内容数据来源:wushujiance.sav某防疫站观察当地一个污水排放口在高温和低温季节中伤寒病菌检出情况。
其中高温和低温季节各观测12次,数据有24个观测样本,有两个属性变量degree 和test,degree有1(高温季节)和2(低温季节)两个等级;test有1(+)和2(-)两个等级。
问:两个季节的伤寒菌检出率有无差别?数据如下图所示:意为:Degree1(高温) 2(低温) 合计 test1(检出)17 8 2(没有检出) 115 16合计121224设A :高温季节;A :低温季节;B :检出;B :没有检出。
记)|(1A B P p =,2p =)|(A B P 此处欲检验0H :21p p =1H ↔:21p p ≠检验统计量:Pearson 卡方统计量=21212211222112)(++++-=n n n n n n n n n χ~)(12χ (渐进)称此检验为卡方检验。
此外,可以证明:卡方检验等价于独立性检验(A 属性与B 属性独立),即:0H :21p p =1H ↔:21p p ≠等价于0H :j i ij p p p ⋅⋅=1H ↔:j i ij p p p ••≠,.2,1,=j i其中nn p ij ij =,nn p i i +•=,n n p j j +•=,.2,1,=j i实验过程:(1)打开数据文件;(2)分析->描述统计->交叉表;相依系数:其数值在0~1之间,但不能达到1,是行变量和列变量相关性的度量指标。


基于多元线性回归全对数模型的人民币汇率水平影响因素分析人民币汇率是指人民币对其他国家货币的比价,是国际经济关系中非常重要的一个指标。
人民币汇率的水平影响着国内外贸易、投资和宏观经济发展,因此人民币汇率的变动一直备受关注。
在国际金融市场上,人民币汇率的波动会对进出口企业、金融机构、政府政策等产生重要影响。
针对人民币汇率的变动问题,经济学家们通过对多元线性回归全对数模型的分析,探究了人民币汇率水平的影响因素。
本文即将通过对基于多元线性回归全对数模型的人民币汇率水平影响因素的分析,深入探讨人民币汇率的变动和影响因素。
一、多元线性回归全对数模型的基本原理多元线性回归全对数模型是一种将因变量和自变量都取对数后的多元线性回归模型。
其基本形式为:ln(Y) = β0 + β1ln(X1) + β2ln(X2) + ... + βnln(Xn) + εY是因变量,X1、X2、...、Xn是自变量,ε为误差项,β0、β1、β2、...、βn是参数。
通过多元线性回归全对数模型的分析,可以得出每一个自变量对因变量的影响程度,以及不同自变量之间的相互影响。
在研究人民币汇率的影响因素时,多元线性回归全对数模型可以帮助研究者理清各个因素对人民币汇率的影响程度,为深入理解人民币汇率的变动提供重要的参考。
二、人民币汇率水平的影响因素分析1. 经济增长水平经济增长水平对人民币汇率有着重要的影响。
通过多元线性回归全对数模型的分析发现,经济增长水平的稳定和增长对人民币汇率的稳定和升值有着积极的影响。
这是因为经济增长水平的稳定和增长会增加外部投资者对人民币的信心,提高人民币的国际地位和需求,从而推动人民币汇率的升值。
2. 贸易顺差贸易顺差是指一个国家的出口额大于进口额,即国家在国际贸易中取得盈余。
通过对多元线性回归全对数模型的分析可以得知,贸易顺差对人民币汇率的影响是正向的。
贸易顺差的增加意味着国家拥有更多外汇储备,这会促使人民银行购买外汇以维持人民币的汇率,从而推动人民币升值。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学院(请填写完整的全名):参赛队员(打印并签名) :1.2.3.日期: 2010 年 5 月 29 日评阅编号(教师评阅时填写):生猪价格问题摘要本文主要就生猪价格下跌原因以及如何制定合理的生猪价格定价策略问题采用线性回归和对数线性模型以及统计学知识对其进行分析。
问题一,采用线性回归法,对猪肉价格的发展趋势进行短期预测。
首先通过对2009年12月到2010年5月我国猪肉价格分析得出,猪肉价格在短期内呈线性下降趋势,得到线性方程^t S a bt =+,然后用根据这个线性方程拟合该时间序列上的猪肉变化趋势,再与实际的变化曲线进行比较,说明此方法的可行性,并对2010年6月的猪肉价格进行预测。
问题二,首先根据猪的不同重量,将猪分为三个成长阶段:5Kg ~25Kg 为幼年期;25Kg ~90Kg 为成长期;90Kg ~110Kg 为成年期。
由于猪的体重从5到110公斤呈正态分布,可以算出这三个阶段的猪的数量比为6:988:6。
然后根据猪场收入与成本建立猪场盈亏平衡点等式模型362%100n X G m ⨯⨯⨯=⨯生。
可以得到猪粮比约为6:1,即该养猪场的盈亏平衡点,从而得问题四出定价策略的数学模型中的猪粮比参数s 。
接着对2009年12月到2010年5月的猪肉价格和猪料价格进行统计,分别求出他们之间的猪料比值。
对数增长的实例和案例分析一、什么是对数增长在实际生活中,我们常常遇到一些状况是呈指数或对数增长的,这些现象可能包括浏览网页的人数、病毒感染的人数、电影票房的收入等。
其中,对数增长是指如果一个数据集在一段时间内增长或缩小了 x 倍,则取对数后,增长或缩小了几个数量级。
对数增长在计算机科学,统计学和数学等领域中都扮演了重要的角色,尤其在机器学习领域,对数增长是很常见的现象。
比如说,在处理图像分类问题时,我们会使用卷积神经网络来对图像进行训练,经过多次的训练迭代之后,神经元数量会呈指数增长,从而导致计算与内存资源的消耗也会呈指数增长。
二、对数增长的实例和案例分析1. 病毒传播模型对数增长的应用最常见的就是在病毒传播模型中。
我们可以将每一个被感染的人视为一个解锁的生产者——他们可以在一段时间内传播着病毒,将病毒传染给其他人。
当病毒传播得越来越广泛时,我们就可以看到一个被感染人数的对数曲线。
这个曲线通常呈指数增长,并且有明显的指数峰值。
通常,我们可以使用线性回归算法来预测病毒传播的峰值时间。
如果我们能够在这个时间之前遏制住病毒的传播,那么就能够有效地阻止病毒的传播。
2. 推特蔓延模型另一个常见的应用是在推特蔓延模型中。
我们可以将推特社交网络看做是一个图。
每个节点代表一个用户,每条边代表一个用户之间的关注关系。
当一个用户在发布一条信息时,这条信息可以被这个用户的关注者们转发给他们的粉丝,从而实现信息的传播。
当推特上的一个话题变得热门时,我们就能看到一个关于转发次数和话题热度的对数曲线。
这个曲线通常呈指数增长,并且有明显的指数峰值。
通过分析这个峰值,我们可以更好地了解何时发布信息会更具影响力。
3. 视频流量模型最后一个常见的应用是在视频流量模型中。
我们可以将视频流量看做是一个关于时间的函数。
当一个视频发布之后,它的流量会从零开始呈指数增长,最终到达一个极限值。
这个增长速度和极限值取决于视频的内容和发布日期。
对于一些热门的视频,我们可以观察到一个关于时长的对数增长曲线,这个增长通常呈现出高峰期和低峰期。
线性与对数模型案例分析----关于农村居民各种不同类型的收入对消费支出影响一、实验目的影响农村居民收入的因素有多种,主要因素可能有以下4项:农业经营收入、工资性收入、财产性收入及转移性收入。
此实验就是研究这四项不同类型收入对消费支出是否有影响,又怎样的影响,建立怎样的模型比较适宜描述农村居民收入的变化。
二、模型设定以下是全国主要地区消费性支出、工资性收入、家庭经营纯收入、财产性收入、转移性收入的数据。
分别设消费性支出、工资性收入、家庭经营纯收入、财产性收入、转移性收入为Y 、1X 、2X 、3X 、4X 。
1、建立如下线性模型 :i X A X A X A X A A Y μ+++++=453423121用Eviews 得到如下回归结果:Dependent Variable: YMethod: Least Squares Date: 06/16/10 Time: 22:54 Sample: 1 32 Included observations: 32Variable Coefficien t Std. Error t-StatisticProb.C 483.4083 253.1362 1.909676 0.0669 X1 0.627140 0.080420 7.798311 0.0000 X2 0.481025 0.115523 4.163869 0.0003 X3 -0.256307 0.906787 -0.282654 0.7796 X4 2.678149 0.616554 4.343738 0.0002 R-squared 0.951902 Mean dependentvar2976.846 Adjusted R-squared 0.944777 S.D. dependentvar1346.774 S.E. of regression 316.4870 Akaike infocriterion 14.49504 Sum squared resid 2704428. Schwarz criterion14.72406 Log likelihood -226.9207 Hannan-Quinncriter.14.57096 F-statistic 133.5893 Durbin-Watsonstat 1.735377 Prob(F-statistic) 0.000000参数估计的结果为:4321^678149.2256307.0481025.062714.04083.483X X X X Y +-++=Se=(253.1326) (0.080420) (0.115523) (0.906787) (0.616554) t=(1.909676) (7.798311) (4.163869) (-0.282654) (4.343738) p= (0.0669) (0.0000) * (0.0003) (0.7796) (0.0002)2R =0.951902 2__R =0.9447772、建立如下双对数回归模型μ+++++=453423121ln ln ln ln ln X B X B X B X B B Y得到如下回归结果:Variable Coefficient Std. Error t-Statistic Prob.C 3.252495 0.749229 4.341125 0.0002 LOG(X1) 0.287918 0.039230 7.339168 0.0000 LOG(X2) 0.184695 0.084019 2.198247 0.0367 LOG(X3) 0.063784 0.055297 1.153485 0.2588 LOG(X4) 0.184094 0.077450 2.376949 0.0248R-squared 0.879103 Mean dependentvar 7.929207Adjusted R-squared 0.861193 S.D. dependentvar 0.349982S.E. of regression 0.130392 Akaike infocriterion -1.093940Sum squared resid 0.459057 Schwarzcriterion -0.864919 Log likelihood 22.50305 F-statistic 49.08282Durbin-Watson stat 2.076804 Prob(F-statistic) 0.000000参数估计结果为:=^ln Y 3.252495+0.287918ln 4321ln 184094.0ln 063784.0ln 184695.0X X X X +++Se= (0.749229) (0.039230) ( 0.084019) (0.055297) (0.077450)t= (4.341125) (7.339168) (2.198247) (1.153485) (2.376949) p= (0.0002) (0.0000) (0.0367) (0.2588) (0.0248)2R =0.879103 2__R =0.861193三、模型检验① 线性模型的检验 1、多重共线性检验(1) 假设2i R 表示变量i X 对于其他变量的回归结果的样本判定系数。
a 、做1X 对其他变量的回归^1X =232.2140+0.0619792X +5.6614973X +2.2881384X21R =0.749576建立F 检验:F=)()1()1(2121k n R k R --- ~ F (k-1,n-k )代入数据得;F=)432()749576.01()14(749576.0---=27.93679原假设0H :21R =0;1H :21R ≠0,在α=0.05的显著水平下,05.0F (3,28)=2.95<F=27.93679。
说明在95%的置信水平下,拒绝原假设: 21R =0。
即1X 与剩余几项存在共线性。
b 、做2X 对其他变量的回归^2X =2043.177+0.0300351X +1.9579213X -1.8915504X22R =0.129974建立F 检验:F=)()1()1(2222k n R k R --- ~ F (k-1,n-k ) 代入数据得;F=)432()129974.01()14(129974.0---=1.394337原假设0H :22R =0;1H :22R ≠0,在α=0.05的显著水平下,05.0F (3,28)=2.95>F =1.394337。
说明在95%的置信水平下,不能拒绝原假设: 21R =0。
即2X 与剩余几项不存在共线性。
c 、做3X 对其他变量的回归^3X =-90.55611+0.0445301X +0.0317782X +0.3839404X23R =0.812587建立F 检验:F=)()1()1(2323k n R k R --- ~ F (k-1,n-k ) 代入数据得;F=)432()812587.01()14(812587.0---=40.46755原假设0H :23R =0;1H :23R ≠0,在α=0.05的显著水平下,05.0F (3,28)=2.95<F =40.46755。
说明在95%的置信水平下,拒绝原假设: 23R =0。
即3X 与剩余几项存在共线性。
d 、做4X 对其他变量的回归^4X =-184.9268+0.0389281X -0.0664072X +0.8304853X24R =0.779290建立F 检验:F=)()1()1(2424k n R k R --- ~ F (k-1,n-k ) 代入数据得;F=)432()779290.01()14(779290.0---=32.95443原假设0H :24R =0;1H :24R ≠0,在α=0.05的显著水平下,05.0F (3,28)=2.95<F =32.95443。
说明在95%的置信水平下,拒绝原假设: 24R =0。
即4X 与剩余几项存在共线性。
2、 异方差检验a 、 残差的图形检验做2e 对Yˆ图形:该图清楚地表明了残差平方与消费性支出是系统相关的。
散点图表明回归方程中很可能存在异方差问题。
b、怀特检验Heteroskedasticity Test: WhiteF-statistic 9.576534 Prob. F(14,17) 0.0000Obs*R-squared 28.39906 Prob.Chi-Square(14) 0.0126Scaled explained SS 52.82365 Prob.Chi-Square(14) 0.0000Test Equation:Dependent Variable: RESID^2Method: Least SquaresDate: 06/21/10 Time: 22:21Sample: 1 32Included observations: 32Variable Coefficient Std. Error t-Statistic Prob.C 640414.2 443785.5 1.443072 0.1672 X1 -262.1711 192.0428 -1.365170 0.1900 X1^2 0.043898 0.041122 1.067498 0.3007 X1*X2 0.139513 0.067067 2.080215 0.0529X1*X3 0.703279 1.156890 0.607905 0.5513 X1*X4 -1.036407 0.822200 -1.260528 0.2245 X2 -332.3679 530.6481 -0.626343 0.5394 X2^2 0.045894 0.152423 0.301093 0.7670 X2*X3 1.961609 1.432246 1.369604 0.1886 X2*X4 -0.740111 0.784698 -0.943179 0.3588 X3 -3185.842 2770.232 -1.150027 0.2661 X3^2 1.609349 7.688052 0.209331 0.8367 X3*X4 -9.409764 12.05343 -0.780671 0.4457 X4 -368.5777 1672.633 -0.220358 0.8282 X4^2 8.870343 5.604688 1.582665 0.1319R-squared 0.887470 Mean dependentvar 84513.38Adjusted R-squared 0.794799 S.D. dependentvar 196283.2S.E. of regression 88914.51 Akaike infocriterion 25.93372Sum squared resid 1.34E+11 Schwarzcriterion 26.62078Log likelihood -399.9395 Hannan-Quinncriter. 26.16146F-statistic 9.576534 Durbin-Watsonstat 1.755984 Prob(F-statistic) 0.000018因为Obs*R-squared 即为2*R n =28.39906。