三角函数的振幅,周期,频率,相位,初相

三角函数的图像和性质1、用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的图像中，五个关键点是：(0,1) (2π,0) (π,-1) (23π,0) (2π,1) 2 sin y x = cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值 当22x k ππ=+时，max 1y =；当22x k ππ=- 时，min 1y =-．当2x k π=时，max 1y =；当2x k ππ=+时，min1y =-．既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数 偶函数 奇函数单调性 在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦上是增函数； 在32,222k k ππππ⎡⎤++⎢⎥⎣⎦上是减函数． 在[]2,2k k πππ-上是增函数； 在[]2,2k k πππ+上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭上是增函数．对称性 对称中心(),0k π 对称轴2x k ππ=+对称中心,02k ππ⎛⎫+ ⎪⎝⎭对称轴x k π=对称中心,02k π⎛⎫⎪⎝⎭无对称轴函数 性质例作下列函数的简图(1)y=|sinx|，x ∈[0，2π]， (2)y=-cosx ，x ∈[0，2π]例利用正弦函数和余弦函数的图象，求满足下列条件的x 的集合：21sin )1(≥x 21cos )2(≤x3、周期函数定义：对于函数()y f x =，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有：()()f x T f x +=，那么函数()y f x =就叫做周期函数，非零常数T 叫做这个函数的周期。

注意： 周期T 往往是多值的（如sin y x = 2π,4π,…,-2π,-4π,…都是周期）周期T 中最小的正数叫做()y f x =的最小正周期（有些周期函数没有最小正周期）sin y x =, cos y x =的最小正周期为2π （一般称为周期）正弦函数、余弦函数：ωπ=2T 。

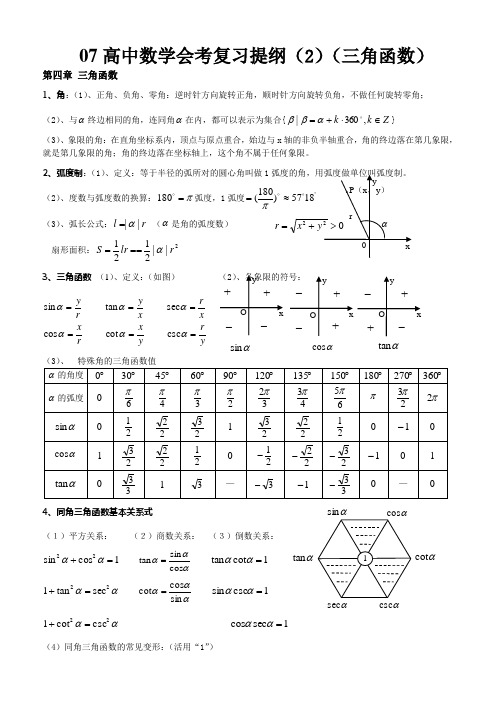
07高中数学会考复习提纲（2）（三角函数）第四章 三角函数1、角：（1）、正角、负角、零角：逆时针方向旋转正角，顺时针方向旋转负角，不做任何旋转零角； （2）、与α终边相同的角，连同角α在内，都可以表示为集合{Z k k ∈⋅+=,360|αββ}（3）、象限的角：在直角坐标系内，顶点与原点重合，始边与x 轴的非负半轴重合，角的终边落在第几象限，就是第几象限的角；角的终边落在坐标轴上，这个角不属于任何象限。

2、弧度制：（1）、定义：等于半径的弧所对的圆心角叫做1（2）、度数与弧度数的换算：π= 180弧度，1弧度)180( =π（3）、弧长公式：r l ||α= （α是角的弧度数） 扇形面积：2||2121r lr S α===3、三角函数 （1）、定义：（如图） （2）、各象限的符号： yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin （3）、 特殊角的三角函数值4、同角三角函数基本关系式（１）平方关系： （２）商数关系： （３）倒数关系：1cos sin 22=+αα αααcos sin tan = 1cot tan =αα αα22sec tan 1=+ αααsin cos cot =1csc sin =αα αα22csc cot 1=+ 1sec cos =αα（4）同角三角函数的常见变形：（活用“1”）αsinx y++ _ _ O xy++__ αcosOαtanxy+ +__O=r αsec αsinαtan αcotcsc①、αα22cos 1sin -=， αα2cos 1sin -±=；αα22sin 1cos -=， αα2sin 1cos -±=；②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+，αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±， |cos sin |2sin 1ααα±=± 5、诱导公式：（奇变偶不变，符号看象限）公式一： ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k 公式二： 公式三： 公式四： 公式五：ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充：ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切)(βα+S ：βαβαβαsin cos cos sin )sin(+=+ )(βα-S ：βαβαβαsin cos cos sin )sin(-=- )(βα+C ：βαβαβsin sin cos cos )cos(-=+a )(βα-C ：βαβαβsin sin cos cos )cos(+=-a )(βα+T ： βαβαβαtan tan 1tan tan )tan(-+=+ )(βα-T ： βαβαβαtan tan 1tan tan )tan(+-=-)(βα+T 的整式形式为：)tan tan 1()tan(tan tan βαβαβα-⋅+=+例：若︒=+45B A ，则2)tan 1)(tan 1(=++B A ．（反之不一定成立） 7、辅助角公式：⎪⎪⎭⎫⎝⎛++++=+x b a b x b a a b a x b x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a（其中ϕ称为辅助角，ϕ的终边过点),(b a ，ab =ϕtan ） （多用于研究性质） 8、二倍角公式：（1）、α2S ： αααcos sin 22sin = （2）、降次公式：（多用于研究性质） α2C ： ααα22sin cos2cos -= ααα2sin 21cos sin =1cos 2sin2122-=-=αα 212cos 2122cos 1sin 2+-=-=ααα α2T ： ααα2tan 1tan 22tan -= 212cos 2122cos 1cos 2+=+=ααα （3）、二倍角公式的常用变形：①、|sin |22cos 1αα=-， |cos |22cos 1αα=+；②、|sin |2cos 2121αα=-， |cos |2cos 2121αα=+③、22sin 1cos sin 21cos sin 22244ααααα-=-=+； ααα2cos sin cos 44=-；④半角：2cos 12sinαα-±=，2cos 12cos αα+±=，αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-= 9、三角函数的图象性质（1）、函数的周期性：①、定义：对于函数f （x ），若存在一个非零常数T ，当x 取定义域内的每一个值时，都有：f （x +T ）= f （x ），那么函数f （x ）叫周期函数，非零常数T 叫这个函数的周期；②、如果函数f （x ）的所有周期中存在一个最小的正数，这个最小的正数叫f （x ）的最小正周期。

三角函数的图像考点回顾： 三角函数图象：y ＝tanx y ＝cotx函数y ＝Asin （ωx ＋φ）的物理意义：振幅|A|，周期2||Tπω=，频率1||2f T ωπ==，相位;x ωϕ+初相ϕ（即当x ＝0时的相位）．（当A ＞0，ω＞0 时以上公式可去绝对值符号）， 三角函数图象的作法：1.几何法（利用三角函数线）2. 描点法：五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）.3.利用图象变换作三角函数图象．三角函数的图象变换有振幅变换、周期变换和相位变换等，重点掌握函数 y ＝Asin （ωx ＋φ）+b （0,0>>ωA ）的作法．（1）振幅变换或叫沿y 轴的伸缩变换．（用y/A （A>0）替换y ）由y ＝sinx 的图象上的点的横坐标保持不变，纵坐标伸长（当A ＞1）或缩短（当0＜A ＜1）到原来的A 倍，得到y ＝Asinx 的图象.（2）周期变换或叫做沿x 轴的伸缩变换．(用ωx （0>ω）替换x)由y ＝sinx 的图象上的点的纵坐标保持不变，横坐标伸长（0＜ω＜1）或缩短（ω＞1）到原来的ω1倍，得到y ＝sin ω x 的图象.（3）相位变换或叫做左右平移．(用x ＋φ替换x)由y ＝sinx 的图象上所有的点向左（当φ＞0）或向右（当φ＜0）平行移动｜φ｜个单位，得到y ＝sin （x ＋φ）的图象.（4）上下平移（用y+(-b)替换y ）由y ＝sinx 的图象上所有的点向上（当b ＞0）或向下（当b ＜0）平行移动｜b ｜个单位，得到y ＝sinx ＋b 的图象.注意：由y ＝sinx 的图象利用图象变换作函数y ＝Asin （ωx ＋φ）+B （A ＞0，ω＞0）（x ∈R ）的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象沿x 轴的伸缩量的区别。

y=cosxy=sinx-11-11ooy xy x例1：函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示，则函数表达式为（ ）A ．)48sin(4π+π-=x yB ．)48sin(4π-π=x yC ．)48sin(4π-π-=x yD ．)48sin(4π+π=x y 答案：A变式1：函数),,0)(sin(R x x A y ∈<>+=πϕωϕω的部分图象如图所示，则函数表达式为_______________ 答案：)23sin(3π-=x y变式2：函数),,0)(sin(R x x A y ∈<>+=πϕωϕω图象如图所示，则函数表达式为_______________ 答案：)62sin(2π+=x y变式3：函数),,0)(sin(R x x A y ∈<>+=πϕωϕω的部分图象如图所示，则函数表达式为_______________ 答案：)32sin(3π+=x y说明：主要从振幅、周期、某点的函数值三个方面考虑，其中变式3要注意1.5不是最高点。

07高中数学会考复习提纲（2）（三角函数）第四章三角函数1、角：（1）、正角、负角、零角：逆时针方向旋转正角，顺时针方向旋转负角，不做任何旋转零角；（2）、与?终边相同的角，连同角?在内，都可以表示为集合{Zkk????,360|????} （3）、象限的角：在直角坐标系内，顶点与原点重合，始边与x轴的非负半轴重合，角的终边落在第几象限，就是第几象限的角；角的终边落在坐标轴上，这个角不属于任何象限。

2、弧度制：（1）、定义：等于半径的弧所对的圆心角叫做1弧度的角，用弧度做单位叫弧度制。

（2）、度数与弧度数的换算：?? 180弧度，1弧度'1857)180(?????（3）、弧长公式：rl||??（?是角的弧度数）扇形面积：2||2121rlrS????3、三角函数（1）、定义：（如图）（2）、各象限的符号：yryxrxxrxyry????????????csccotcossectansin（3）、特殊角的三角函数值2?cos1232221021?22?23?1?01?tan03313—3?1?33?0—04、同角三角函数基本关系式（１）平方关系：（２）商数关系：（３）倒数关系：1cossin22???????cossintan?1cottan?????22sectan1?????sincoscot?1cscsin?????22csccot1??1seccos???（4）同角三角函数的常见变形：（活用“1”）①、??22cos1sin??，??2cos1sin???；??22sin1cos??，??2sin1cos???；②???????2sin2cossinsincoscottan22????，?????????2cot22sin2cos2cossinsincostancot22??????sin xy+ + _ _O xy++__ ?cos O?tan xy+ +__O? P（x，y）r x 0022???yxr y?sec?sin?cos?tan?cot?csc 1③?????2sin1cossin21)cos(sin2?????，|cossin|2sin1??????5、诱导公式：（奇变偶不变，符号看象限）公式一：??????tan)360tan(cos)360cos(sin)360sin(????????????kkk公式二：??????tan)180tan(cos)180cos(sin)180sin(?????????????????tan)180tan(cos)180cos(sin)180sin(?????????????????tan)tan(cos)cos(sin)sin(??????????????tan)360tan(cos)360cos(sin)360sin(???????????．补充：?????????cot)2sin)2cos)2sin(???????????????cot)2sin)2cos)2sin(?????????????????cot)23sin)23cos)23sin(?????????????????cot)23sin)23cos)23???????6、两角和与差的正弦、余弦、正切)(???S：??????sincoscossin)sin(???)(???S：??????sincoscossin)sin(???)(???C：?????sinsincoscos)cos(???a)(???C：?????sinsincoscos)cos(???a)(???T：??????tantan1tantan)tan(????)(???T：??????tantan1tantan)tan(????)(???T的整式形式为：)tantan1()tan(tantan???????????例：若???45BA，则2)tan1)(tan1(???BA．（反之不一定成立）7、辅助角公式：??????????????xbabxbaabaxbxacossincossin222222)sin()sincoscos(sin2222????????????xbaxxba（其中?称为辅助角，?的终边过点),(ba，ab??tan）（多用于研究性质）8、二倍角公式：（1）、?2S：???cossin22sin?（2）、降次公式：（多用于研究性质）?2C：???22sincos2cos?????2sin21cossin?1cos2sin2122??????212cos2122cos1sin2?????????2T：???2tan1tan22tan??212cos2122cos1cos2???????（3）、二倍角公式的常用变形：①、|sin|22cos1????，|cos|22cos1????；②、|sin|2cos2121????，|cos|2cos2121????③、22sin1cossin21cossin22244??????????；???2cossincos44??；④半角：2cos12sin????? ，2cos12cos????? ，???cos1cos12tan????????cos1sinsincos1????9、三角函数的图象性质（1）、函数的周期性：①、定义：对于函数f（x），若存在一个非零常数T，当x取定义域内的每一个值时，都有：f（x+T）= f（x），那么函数f（x）叫周期函数，非零常数T叫这个函数的周期；②、如果函数f（x）的所有周期中存在一个最小的正数，这个最小的正数叫f （x）的最小正周期。

07高中数学会考复习提纲（2）（三角函数）第四章 三角函数1、角：（1）、正角、负角、零角：逆时针方向旋转正角，顺时针方向旋转负角，不做任何旋转零角； （2）、与α终边相同的角，连同角α在内，都可以表示为集合{Z k k ∈⋅+=,360|αββ}（3）、象限的角：在直角坐标系内，顶点与原点重合，始边与x 轴的非负半轴重合，角的终边落在第几象限，就是第几象限的角；角的终边落在坐标轴上，这个角不属于任何象限。

2、弧度制：（1）、定义：等于半径的弧所对的圆心角叫做1（2）、度数与弧度数的换算：π=180弧度，1弧度)180(=π（3）、弧长公式：r l ||α= （α是角的弧度数） 扇形面积：2||2121r lr S α===3、三角函数 （1）、定义：（如图） （2）、各象限的符号：yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin （3）、 特殊角的三角函数值4、同角三角函数基本关系式（１）平方关系： （２）商数关系： （３）倒数关系：1cos sin 22=+αα αααcos sin tan =1cot tan =αα αα22sec tan 1=+ αααsin cos cot =1csc sin =αα αα22csc cot 1=+ 1sec cos =αααsinx y+ + _ _ Oxy+ +__ αcosOαtanxy+ +_ _O=r αsec αsinαtan αcotαcsc（4）同角三角函数的常见变形：（活用“1”）①、αα22cos 1sin -=， αα2cos 1sin -±=；αα22sin 1cos -=， αα2sin 1cos -±=；②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+，αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±， |cos sin |2sin 1ααα±=± 5、诱导公式：（奇变偶不变，符号看象限）公式一： ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k 公式二： 公式三： 公式四： 公式五：ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充：ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切)(βα+S ：βαβαβαsin cos cos sin )sin(+=+ )(βα-S ：βαβαβαsin cos cos sin )sin(-=- )(βα+C ：βαβαβsin sin cos cos )cos(-=+a )(βα-C ：βαβαβsin sin cos cos )cos(+=-a )(βα+T ： βαβαβαtan tan 1tan tan )tan(-+=+ )(βα-T ： βαβαβαtan tan 1tan tan )tan(+-=-)(βα+T 的整式形式为：)tan tan 1()tan(tan tan βαβαβα-⋅+=+例：若︒=+45B A ，则2)tan 1)(tan 1(=++B A ．（反之不一定成立）7、辅助角公式：⎪⎪⎭⎫⎝⎛++++=+x b a b x b a a b a x b x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a（其中ϕ称为辅助角，ϕ的终边过点),(b a ，ab =ϕtan ） （多用于研究性质） 8、二倍角公式：（1）、α2S ： αααcos sin 22sin = （2）、降次公式：（多用于研究性质） α2C ： ααα22sin cos 2cos -= ααα2sin 21cos sin =1cos 2sin2122-=-=αα 212cos 2122cos 1sin 2+-=-=ααα α2T ： ααα2tan 1tan 22tan -= 212cos 2122cos 1cos 2+=+=ααα （3）、二倍角公式的常用变形：①、|sin |22cos 1αα=-， |cos |22cos 1αα=+；②、|sin |2cos 2121αα=-， |cos |2cos 2121αα=+③、22sin 1cos sin 21cos sin 22244ααααα-=-=+； ααα2cos sin cos 44=-；④半角：2cos 12sinαα-±=，2cos 12cos αα+±=，αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-= 9、三角函数的图象性质（1）、函数的周期性：①、定义：对于函数f （x ），若存在一个非零常数T ，当x 取定义域内的每一个值时，都有：f （x +T ）= f （x ），那么函数f （x ）叫周期函数，非零常数T 叫这个函数的周期；②、如果函数f （x ）的所有周期中存在一个最小的正数，这个最小的正数叫f （x ）的最小正周期。

精解三角函数的周期性一、正弦函数的周期三角函数，以正弦函数y = sin x为代表，是典型的周期函数.幂函数y = xα 无周期性，指数函数y = a x无周期性，对数函数y =log a x无周期，一次函数y = kx+b、二次函数y = ax2+bx+c、三次函数y = ax3+bx2 + cx+d无周期性.周期性是三角函数独有的特性.1、正弦函数y=sin x的最小正周期在单位圆中，设任意角α的正弦线为有向线段MP.正弦函数的周期性动点P每旋转一周，正弦线MP的即时位置和变化方向重现一次.同时还看到，当P的旋转量不到一周时，正弦线的即时位置包括变化方向不会重现.因此，正弦函数y=sin x的最小正周期2π.2、y=sin（ωx）的最小正周期设ω>0，y =sin（ωx）的最小正周期设为L .按定义y= sin ω（x+L）= sin（ωx+ ωL）= sinωx .令ωx = x则有sin （x+ ωL）= sin x因为sin x最小正周期是2π，所以有例如sin2x的最小正周期为sin的最小正周期为3、正弦函数y=sin（ωx+φ）的周期性对正弦函数sin x的自变量作“一次替代”后，成形式y = sin （ωx+φ）. 它的最小正周期与y = sinωx的最小正周期相同，都是.如的最小周期与y = sin（3x）相同，都是.于是，余弦函数的最小正周期与sin x的最小正周期相同，都是2π.二、复合函数的周期性将正弦函数y = sin x进行周期变换x→ωx，sin x→sinωx后者周期变为而在以下的各种变换中，如（1）初相变换sinωx→si n（ωx+φ）；（2）振幅变换sin（ωx+φ）→A sin（ωx+φ）；（3）纵移变换A si n（ωx+φ）→A si n（ωx+φ）+m；后者周期都不变，亦即A si n（ωx+φ）+m与si n（ωx）的周期相同，都是.而对复合函数f（sin x）的周期性，由具体问题确定.1、复合函数f（sin x）的周期性【例题】研究以下函数的周期性：（1）2 sin x；（2）（2）的定义域为［2kπ，2kπ+π］，值域为［0，1］，作图可知，它是最小正周期为2π的周期函数.【解答】（1）2sin x的定义域为R，值域为，作图可知，它是最小正周期为2π的周期函数.【说明】从基本函数的定义域，值域和单调性出发，通过作图，还可确定，log a x，sin x，，sin（sin x）都是最小正周期2π的周期函数.2、y= sin3x的周期性对于y = sin3x =(sin x)3，L=2π肯定是它的周期，但它是否还有更小的周期呢我们可以通过作图判断，分别列表作图如下.图上看到，y = sin3x没有比2π更小的周期，故最小正周期为2π.3、y= sin2x的周期性对于y = sin2x = (sin x)2，L=2π肯定是它的周期，但它的最小正周期是否为2π可以通过作图判定，分别列表作图如下.图上看到，y = sin2x的最小正周期为π，不是2π.4、sin2n x和sin2n-1x的周期性y = sin2x的最小正周期为π，还可通过另外一种复合方式得到. 因为cos2x的周期是π，故sin2x的周期也是π.sin2x的周期，由cos x的2π变为sin2x的π. 就是因为符号法“负负得正”所致.因此，正弦函数sin x的幂符合函数sin m x，当m=2n时，sin m x的最小正周期为π；m = 2n–1时，sin m x的最小正周期是2π.5、幂复合函数举例【例1】求y =|sin x|的最小正周期.【解答】最小正周期为π.【例2】求的最小正周期.【解答】最小正周期为2π.【例3】求的最小正周期.【解答】最小正周期为π.【说明】正弦函数sin x的幂复合函数.当q为奇数时，周期为2π；q为偶数时，周期为π.三、周期函数的和函数两个周期函数，如sin x和cos x，它们最小正周期相同，都是2π. 那么它们的和函数，即si nx + cos x的最小正周期如何和函数的周期与原有函数的周期保持不变. 这个结论符合一般情况. 对于另一种情况，当相加的两个函数的最小正周期不相同，情况将会如何1、函数sin x + sin2 x的周期性sin x的最小正周期为2π，sin2x的最小正周期是π，它们之间谁依谁，或依赖一个第三者列表如下.表上看到函数sin x+sin2x的最小正周期是2π.2、函数sin x + sin2x的周期性依据上表，作sin x+sin2x的图像如右.从图上看到，函数的最小正周期为2π. 由si nx，sin2x的最小正周期中的大者决定，因为前者是后者的2倍.从图上看到，sin x+sin2x仍然是个“振动函数”，但振幅已经不是常数了.3、函数sin x+sin x的周期性sin x的最小正周期为2π，sin x的最小正周期是3π.们之间的和sin x + sin x的最小正周期也由“较大的”决定吗即“和函数”的周期为3π吗不妨按周期定义进行检验. 设则x0+3π=因此3π不是sin x + sin x的最小正周期.通过作图、直观看到，sin x+sin x的最小正周期为6π，即sin x和sin x最小正周期的最小倍数.。

高中数学(三角函数)零角：逆时针方向旋转正角，顺时针方向旋转负角，不做任何旋转零角; 连同角&在内，都可以表示为集合{0丨0 = & +「360°山wZ}(3)、象限的许J ：在肓和坐标系内，顶点与原点重合，始边与x 轴的非负半轴重合，角的终边落在第几象限, 就是笫儿象限的角；角的终边落在处标轴上，这个角不属于任何象限。

2、弧度制：(1)、定义：等于半径的弧所对的圆心角叫做1弧度的角，用弧度做单位叫弧度制。

1 QH (2).度数与弧度数的换算：180° 弧度，1弧度=(——)，57°18‘71(3)、弧长公式：I =\a\r (a 是角的弧度数)sin 2<z + cos 26z = l tan^=^^cos a(4)同角三角函数的常见变形：(活用“1”)(s)(sina ±cos a)2 = l±2sinacosQ = l±sin2a,5、诱导公式：(奇变偶不变，符号看象限)公式一：sin(a + k - 360°) = sin a cos(a + R - 360°) = cos a tan(a + k - 360°) = tana\p (xy)-\2 >0 y1扇形面积:(2)、 4、同角三角函数基本关系式 (1)平方关系:(2 )商数关系:S = —lr == — \a\r 22 2第四章三角函数1、角:(1)、正角、负角、 (2 )、与Q 终边相同的角, ①.sirr a = l — cos~ a ,sin a = ±vl-cos 2cr ； cos 2 cr = 1-sin 2 cr, cos a = ±Vl-sin 2cr ；A /1 ±sin 2a =1 sin Q 土 cos a Isin(— + a) = cos a sin(— -cz) = -coscz sin(— + a) = -cos a2 2 2 cos(y + ◎) = 一sin a cos(^- - a) = - sin a cos (号 + a) = sin a6、两角和与差的正弦、余弦、正切S (a+0)： sin(a + 0) =s in a cos 0 + cos a sin (3 Sg" sin (6z-/?) =sin a cos 0 - cos a sin 0C(a+0)： COS(d+0) =cos a cos 0 - sin & sin 0 C (_#): cos(d - 0) = cos a cos 0 + sin a sin /3T(a+0):tan© + 0)tan Q + tan 0 1 - tan cr tan 0T(a-/j ):tan(o - 0)=tan Q - tan 0I + tan (7 tan 0T (a+ft ｝的整式形式为： tan a + tan 0 = tan(cr + 0) • (1 - tan a tan 0)例：若 71 + B = 45° ,则(1 + tan A)(\ + tan B) = 2 .(反Z 不一•定成立)=J/ +/?2(sin x • cos (p + cos x • sin (p) = V^z 2 +/?2 • sin(x + (p)(其中©称为辅助角，0的终边过点(a,b), tan^9 =—)(多用于研究性质) a8、二倍角公式：(1)、S 2a : sin 2& = 2sin a cos &(3)^ 二倍角公式的常丿 IJ 变形：①k 71 - cos 2a = V2 I sin cr I, Jl + cos2a =V2 I cos a I ；公式二：sin(180o -tz) = sin a cos(l 80° -a) = - cos a tan(l 80° -a) = - tana 补充：公式三： sin(l 80° + a) = -sin a cos(l 80° + a) = - cos a tan(180° + a) = tana公式四: sin(-a) = -sin a cos(-tz) = COS6Z tan(-ez) = - tan «公式五：sin(360° -a) = -sin a cos(360°-a) = cos a tan(360° -<z) = -tancrsin(y - ct) = coscz cos (守-Q ) = sin7、辅助角公式: asinx + bcosx = Ja ，+b?, _____ s i“+〒L= +b 2 yja 2 +b 2 \cosx丿(2)、降次公式：(多用于研究性质)aacos 2a = cos a-sin a=1 -2 sin 2 a - 2cos 2 a 一 1tan 2a =2 tan a1-tan 2 asin a cos a = —sin 2a2.9 1 - cos 2a 1 小 1sirr a = -------------- =——cos 2a + —2 2 221 + cos 2a 1 c 1 cos 「a = ------------- = —coszcr + —2 2 2②、J*-*cosN =1 sina I,J 丄 + 丄 cos la =1 cos a IV2 2③、• 4 4 1 c • 22 1 sin 2asin a + cos a = l-2sirr acos a - 1 ----------------------- cos4(2 - sin4a = cos2a ；9、三角函数的图象性质(1) 、函数的周期性：①、定义：对于函数f (x),若存在一个非零常数T,当兀取定义域内的每一个值时, 都有：f (x+T) =/(x),那么函数/(x)叫周期函数，非零常数T 叫这个函数的周期；②、如果函数/(x)的所有周期中存在一个最小的匸数，这个最小的匸数叫/(%)的最小正周期。

三角函数的图像与性质一、正弦函数、余弦函数的图像与性质
(
二、正切函数的图象与性质
三、三角函数图像的平移变换和伸缩变换
1. 由x y sin =的图象得到)sin(ϕω+=x A y (0,0A ω>>)的图象
注意：图象时一定要注意平移与伸缩的先后顺序，否则会出现错误。

2. )sin(ϕω+=x A y (0,0A ω>>)的性质
（1）定义域、值域、单调性、最值、对称性：
将ϕω+x 看作一个整体，与相应的简单三角函数比较得出； （2）奇偶性：只有当ϕ取特殊值时，这些复合函数才具备奇偶性：
)sin(ϕω+=x A y ，当πϕk =时为奇函数，当2
ππϕ±=k 时为偶函数；
（3）最小正周期：ω
π2=T
3. y ＝A sin(ωx ＋φ), x ∈[0,+∞) (0,0A ω>>)中各量的物理意义
(1) A 称为振幅； (2)2T πω
=称为周期；
(3)1f
T
=
称为频率；
(4)x ωϕ+称为相位；
(5)ϕ称为初相 (6)ω称为圆频率.。

三角函数的性质及其应用 编稿：李霞 审稿：孙永钊【考纲要求】1、了解函数sin()y A x ωϕ=+的物理意义；能画出sin()y A x ωϕ=+的图象，了解参数A ，ω，ϕ对函数图象变化的影响.2、了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题. 【知识网络】【考点梳理】考点一、函数sin()y A x ωϕ=+(0A >,0ω>)的图象的作法1.五点作图法：作sin()y A x ωϕ=+的简图时，常常用五点法，五点的取法是设t x ωϕ=+，由t 取0、2π、π、32π、2π来求相应的x 值及对应的y 值，再描点作图。

2．图象变换法：（1）振幅变换:把sin y x =的图象上各点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A 倍（横坐标不变），得到sin y A x =的图象；（2）相位变换:把sin y A x =的图象上所有点向左(ϕ>0)或向右(ϕ<0)平行移动|ϕ|个单位，得到sin()y A x ϕ=+的图象；（3）周期变换:把sin()y A x ϕ=+的图象上各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的ω1倍（纵坐标不变），可得到sin()y A x ωϕ=+的图象.（4）若要作sin()y A x b ϕ=++，可将sin()y A x ϕ=+的图象向上(0)b >或向下(0)b <平移b 个单位，可得到sin()y A x b ϕ=++的图象．记忆方法仍为“左加右减，上正下负，纵伸(A>1)横缩(ω>1)”。

要点诠释：由sin y x =的图象利用图象变换作函数sin()y A x ωϕ=+的图象时要特别注意：当周期变换和相位变换的先后顺序不同时，原图象沿x 轴的伸缩量有区别.图象的作法三角函数的性质及其应用图象的性质考点二、sin()y A x ωϕ=+的解析式 1. sin()y A x ωϕ=+的解析式sin()y A x ωϕ=+(0A >, 0ω>)，[0,)x ∈+∞表示一个振动量时，A 叫做振幅，2T πω=叫做周期，12f T ωπ==叫做频率，x ωϕ+叫做相位，0x =时的相位ϕ称为初相. 2. 根据图象求sin()y A x ωϕ=+的解析式求法为待定系数法，突破口是找准五点法中的第一零点(,0)ϕω-. 求解步骤是先由图象求出A 与T ，再由2Tπω=算出ω，然后将第一零点代入0x ωϕ+=求出ϕ. 要点诠释：若图象未标明第一零点，就只能找特殊点用待定系数法计算. 考点三、函数sin()y A x ωϕ=+(0A >,0ω>)的性质1. 定义域: x R ∈,值域:y ∈[-A,A]. 2．周期性: 2T πω=3. 奇偶性:2k πϕπ=+时为偶函数；k ϕπ=时为奇函数，k Z ∈.4．单调性:单调增区间:[ωϕππωϕππ-+--22,22k k ] , k Z ∈ 单调减区间:[ωϕππωϕππ-+-+232,22k k ] , k Z ∈ 5. 对称性:对称中心(ωϕπ-k ,0)， k Z ∈；对称轴x=ωϕππ-+2k ，k Z ∈6．最值: 当22x k πωϕπ+=+即22k x ππϕω+-=时，y 取最大值A当22x k πωϕπ+=-即22k x ππϕω--=时，y 取最小值-A ．(k Z ∈).要点诠释：①求周期、单调区间、最值时一般先将函数式化为sin()y A x ωϕ=+，要特别注意A 、ω的正负，再把x ωϕ+看作一个整体，并结合基本三角函数的图象和性质解出即可；利用单调性比较三角函数大小一般要化为同名函数,并且在同一单调区间；②整体代换和数形结合是三角函数学习中重要的思想方法，在学习中，很多三角函数的问题都是通过整体代换并观察基本三角函数的图象而得到的。

三角函数公式总结与推导1. ①与（0°≤＜360°）终边相同的角的集合（角与角的终边重合）：αααβ{}Zk k ∈+⨯=,360|αββ ②终边在x 轴上的角的集合：{}Z k k ∈⨯=,180|ββ③终边在y 轴上的角的集合：{}Zk k ∈+⨯=,90180|ββ④终边在坐标轴上的角的集合：{}Z k k ∈⨯=,90| ββ⑤终边在y =x 轴上的角的集合：{}Z k k ∈+⨯=,45180| ββ⑥终边在轴上的角的集合：x y -={}Zk k ∈-⨯=,45180| ββ⑦若角与角的终边关于x 轴对称，则角与角的关系：αβαββα-=k 360⑧若角与角的终边关于y 轴对称，则角与角的关系：αβαββα-+= 180360k ⑨若角与角的终边在一条直线上，则角与角的关系：αβαββα+=k 180⑩角与角的终边互相垂直，则角与角的关系：αβαβ90360±+=βαk 2. 角度与弧度的互换关系：360°=2 180°= 1°=0.01745 1=57.30°=57°18′ππ注意：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.、弧度与角度互换公式： 1rad ＝°≈57.30°=57°18ˊ．1°＝≈0.01745（rad ）π180180π3、弧长公式：. 扇形面积公式：r l⋅=||α211||22s lr r α==⋅扇形4、三角函数：设是一个任意角，在的终边上任取（异于原点的）一点P （x,y ）P 与原点的距离为ααr ，则 ； ； ； ； ；.ry =αsin rx =αcos xy =αtan yx =αcot xr =αsec .yr=αcsc 5、三角函数在各象限的符号：（一全二正弦，三切四余弦）、、、、、、、、、、、、、、、1¡¢2¡¢3¡¢4表示第一、二、三、四象限一半所在区域的6、三角函数线正弦线：MP; 余弦线：OM; 正切线： AT.7. 三角函数的定义域：三角函数定义域sin x=)(x f {}R x x ∈|cos x =)(x f {}R x x ∈|tan x =)(x f ⎭⎬⎫⎩⎨⎧∈+≠∈Z k k x R x x ,21|ππ且cot x =)(x f {}Z k k x R x x ∈≠∈,|π且sec x =)(x f ⎭⎬⎫⎩⎨⎧∈+≠∈Z k k x R x x ,21|ππ且csc x=)(x f {}Z k k x R x x ∈≠∈,|π且8、同角三角函数的基本关系式：αααtan cos sin =αααcot sin cos =1cot tan =⋅αα1sin csc =α⋅α1cos sec =α⋅α 1cos sin 22=+αα1tan sec 22=-αα1cot csc 22=-αα9、诱导公式：2k παα±把的三角函数化为的三角函数，概括为：“奇变偶不变，符号看象限” 三角函数的公式：（一）基本关系公式组二公式组三x x k x x k xx k x x k cot )2cot(tan )2tan(cos )2cos(sin )2sin(=+=+=+=+ππππxx x x xx x x cot )cot(tan )tan(cos )cos(sin )sin(-=--=-=--=-公式组四 公式组五 公式组六x x x x xx x x cot )cot(tan)tan(cos )cos(sin )sin(=+=+-=+-=+ππππx x x x xx x x cot )2cot(tan )2tan(cos )2cos(sin )2sin(-=--=-=--=-ππππxx x x xx x x cot )cot(tan )tan(cos )cos(sin )sin(-=--=--=-=-ππππ（二）角与角之间的互换公式组一sin x ·csc x =1tan x =x x cos sin sin 2x +cos 2x =1cos x ·sec x x =xxsin cos 1+tan 2x =sec 2xtan x ·cot x =11+cot 2x =csc 2x=1(3) 个 o<x<2,个sinx<x<tanx16. 个个个个个个:公式组一 公式组二 βαβαβαsin sin cos cos )cos(-=+αααcos sin 22sin = βαβαβαsin sin cos cos )cos(+=-ααααα2222sin 211cos 2sin cos 2cos -=-=-=βαβαβαsin cos cos sin )sin(+=+ααα2tan 1tan 22tan -= βαβαβαsin cos cos sin )sin(-=-2cos 12sinαα-±=βαβαβαtan tan 1tan tan )tan(-+=+2cos 12cosαα+±=βαβαβαtan tan 1tan tan )tan(+-=-公式组三公式组四 公式组五2tan 12tan2sin 2ααα+= 2tan 12tan 1cos 22ααα+-= 2tan 12tan2tan 2ααα-=,,,.42675cos 15sin -== 42615cos 75sin +== 3275cot 15tan -== 3215cot 75tan +== 10. 正弦、余弦、正切、余切函数的图象的性质：()ϕω+=x A y sin （A 、＞0）ω定义域RRR值域]1,1[+-]1,1[+-R R []A A ,-周期性 π2π2ππωπ2奇偶性奇函数偶函数奇函数奇函数当非奇非偶,0≠ϕ当奇函数,0=ϕ()()[]()()[]()()[]()()[]βαβαβαβαβαβαβαβαβαβαβαβα--+-=-++=--+=-++=cos cos 21sin sin cos cos 21cos cos sin sin 21sin cos sin sin 21cos sin 2cos 2sin 2sin sin βαβαβα-+=+2sin 2cos 2sin sin βαβαβα-+=-2cos 2cos 2cos cos βαβαβα-+=+2sin 2sin 2cos cos βαβαβα-+-=-αααααααsin cos 1cos 1sin cos 1cos 12tan-=+=+-±=⎭⎬⎫⎩⎨⎧∈+≠∈Z k k x R x x ,21|ππ且{}Z k k x R x x ∈≠∈,|π且xy cot =x y tan =xy cos =xy sin =ααπsin )21cos(-=+ααπcos )21sin(=+ααπcot )21tan(-=+ααπsin )21cos(=-ααπcos )21sin(=-ααπcot )21tan(=-单调性]22,22[ππππk k ++-上为增函数；]223,22[ππππk k ++上为减函数（）Z k ∈()]2,12[ππk k -；上为增函数()]12,2[ππ+k k 上为减函数（）Z k ∈⎪⎭⎫⎝⎛++-ππππk k 2,2上为增函数（）Z k ∈上为减函()()ππ1,+k k 数（）Z k ∈⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--+--)(212),(22A k A k ωϕππωϕππ上为增函数；⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--+-+)(232),(22A k A k ωϕππωϕππ上为减函数（）Z k ∈注意：①与的单调性正好相反；与的单调性也同样相反.一般地，若x y sin -=x y sin =x y cos -=x y cos =在上递增（减），则在)(x f y =],[b a )(x f y -=],[b a ②与的周期是.x y sin =x y cos =π③或（）的周期.)sin(ϕω+=x y )cos(ϕω+=x y 0≠ωωπ2=T 的周期为2（，如图，翻折无效）.2tanx y =ππωπ2=⇒=T T ④的对称轴方程是（），对称中心（）；的对称轴方程是)sin(ϕω+=x y 2ππ+=k x Z k ∈0,πk )cos(ϕω+=x y （），对称中心（）；的对称中心（）.πk x =Z k ∈0,21ππ+k )tan(ϕω+=x y 0,2πk xx y x y 2cos )2cos(2cos -=--=−−−→−=原点对称⑤当·；·.αtan ,1tan =β)(2Z k k ∈+=+ππβααtan ,1tan -=β)(2Z k k ∈+=-ππβα⑥与是同一函数,而是偶函数，则x y cos =⎪⎭⎫ ⎝⎛++=ππk x y 22sin )(ϕω+=x y )cos()21sin()(x k x x y ωππωϕω±=++=+=.⑦函数在上为增函数.（×） [只能在某个单调区间单调递增. 若在整个定义域，为x y tan =R x y tan =增函数，同样也是错误的].⑧定义域关于原点对称是具有奇偶性的必要不充分条件.（奇偶性的两个条件：一是定义域关于原)(x f 点对称（奇偶都要），二是满足奇偶性条件，偶函数：，奇函数：）)()(x f x f =-)()(x f x f -=-奇偶性的单调性：奇同偶反. 例如：是奇函数，是非奇非偶.（定义域不关于原x y tan =)31tan(π+=x y 点对称）奇函数特有性质：若的定义域，则一定有.（的定义域，则无此性质）x ∈0)(x f 0)0(=f x ∉0⑨x y sin =不是周期函数；为周期函数（）x y sin =π=T 是周期函数（如图）；为周期函数（x y cos =x y cos ==T 的周期为（如图），并非所有周期函数都有最小正周期，例如： 212cos +=x y π.R k k x f x f y ∈+===),(5)(⑩ 有.abb a b a y =+++=+=ϕϕαβαcos )sin(sin cos 22y b a ≥+2211、三角函数图象的作法：１）、几何法：２）、描点法及其特例——五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）.３）、利用图象变换作三角函数图象．三角函数的图象变换有振幅变换、周期变换和相位变换等．函数y ＝Asin （ωx ＋φ）的振幅|A|，周期，频率，相位初相（即当x ＝02||T πω=1||2f T ωπ==;x ωϕ+ϕ时的相位）．（当A ＞0，ω＞0 时以上公式可去绝对值符号），由y ＝sinx 的图象上的点的横坐标保持不变，纵坐标伸长（当|A|＞1）或缩短（当0＜|A|＜1）到原来的|A|倍，得到y ＝Asinx 的图象，叫做振幅变换或叫沿y 轴的伸缩变换．（用y/A 替换y ）由y ＝sinx 的图象上的点的纵坐标保持不变，横坐标伸长（0＜|ω|＜1）或缩短（|ω|＞1）到原来的倍，得到y ＝sin ω x 的图象，叫做周期变换或叫做沿x 轴的伸缩变换．(用ωx 替换x)1||ω由y ＝sinx 的图象上所有的点向左（当φ＞0）或向右（当φ＜0）平行移动｜φ｜个单位，得到y ＝sin （x ＋φ）的图象，叫做相位变换或叫做沿x 轴方向的平移．(用x ＋φ替换x)由y ＝sinx 的图象上所有的点向上（当b ＞0）或向下（当b ＜0）平行移动｜b ｜个单位，得到y ＝sinx ＋b 的图象叫做沿y 轴方向的平移．（用y+(-b)替换y ）由y ＝sinx 的图象利用图象变换作函数y ＝Asin （ωx ＋φ）（A ＞0，ω＞0）（x ∈R ）的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象延x 轴量伸缩量的区别。