(整理)高一数学向量的加减法
- 格式:doc
- 大小:166.00 KB
- 文档页数:5

高中学生学科素质训练高一数学同步测试(9)—向量的加减法、实数与向量的乘积一、选择题(每小题5分,共60分,请将所选答案填在括号内)1.如图,已知四边形ABCD 是梯形,AB ∥CD ,E 、F 、G 、H 分别是AD 、BC 、AB 与CD 的中点,则EF 等于( )A .BC AD +B .DC AB +C .DH +D .GH +2.下列说法正确的是 ( ) A .方向相同或相反的向量是平行向量 B .零向量的长度为0C .长度相等的向量叫相等向量D .共线向量是在同一条直线上的向量3.在△ABC 中,D 、E 、F 分别BC 、CA 、AB 的中点,点M 是△ABC 的重心,则 MC MB MA -+等于( )A .B .4C .4D .4 4.已知向量与反向,下列等式中成立的是( ) A .||||||b a b a -=- B .||||b a b a -=+C .||||||b a b a -=+D .||||||b a b a +=+5.在 ABCD 中,设====,,,,则下列等式中不正确的是( ) A .=+ B .=-C .=-D .=-6.下列各量中是向量的是( ) A .质量 B .距离C .速度D .电流强度7.在矩形ABCD 中,O 是对角线的交点,若OC e DC e BC 则213,5=== ( )A .)35(2121e e + B .)35(2121e e - C .)53(2112e e - D .)35(2112e e - 8.若),,(,,,R ∈=+μλμλ不共线则( )A .==,B .o ==μ,C .o ==,λD .o o ==μλ, 9.化简)]24()82(21[31b a b a --+的结果是( )A .-2B .-2C .-D .-10.下列三种说法:①一个平面内只有一对不共线向量可作为表示该平面所有向量的基底 ②一个平面内有无数对不共线向量可作为该平面的所有向量的基底 ③零向量不可作为基底中的向量。

向量的加法口诀: 首尾相连,首连尾,方向指向末向量。
以第一个向量的起点为起点,以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算,图像如下图所示:向量的减法口诀: 首首相连,尾连尾,方向指向被减向量。
以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容,要求同学们会向量的基本运算,其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算,学会运用图像解决向量加减法,向量的数乘等问题。
向量的相关题目难度也不是很大,只要大家认真学习,认真做好笔记,认真做做题目,总结做题规律,那么当我们遇到类似题目时就会似曾相识,做起来也很顺手,再细心点的话,得满分也没有问题。
学习方法很多,重要的事找到适合自己的方法,当然适合自己方法就是最好的方法。
附一;三角形定则解决向量加减的方法将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减,则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的λ∣倍;当∣λ∣<1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义:已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义:两个向量的数量积(内积、点积)是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示:a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a(交换律);(λa)·b=λ(a·b)(关于数乘法的结合律);(a+b)·c=a·c+b·c(分配律);向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即:由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b.若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积.。


向量一、平面向量的加法和乘积1、向量加法的交换律:a b b a +=+2、向量加法的结合律:()()a b c a b c ++=++3、向量乘积的结合律:()()a a λμλμ=4、向量乘积的第一分配律:()a a a λμλμ+=+5、向量乘积的第二分配律:()a b a b λλλ+=+二、平面向量的基本定理如果1e 、2e 是同一平面内的两个不是共线的向量,那么对于这一平面内的任一a ,有且只有一对实数1λ、2λ,使得1122a e e λλ=+。
(1)我们把不是共线的1e 、2e 叫做表示这一平面内所有向量的一组基底;(2)基底不是唯一的,关键是不是共线;(3)由定理可以将平面内任一a 在给出基底1e 、2e 的条件下进行分解;(4)基底给定时,分解形式是唯一的,1λ、2λ是被a 、1e 、2e 唯一确定的数量。
三、平面向量的直角坐标运算1、已知11(,)a x y =,22(,)b x y =,则1212(,)a b x x y y +=++,1212(,)a b x x y y -=--,1212(,)a b x x y y ⋅=.2、已知11(,)A x y ,22(,)B x y ,则22112121(,)(,)(,)AB OB OA x y x y x x y y =-=-=--。
3、已知11(,)a x y =和实数λ,则1111(,)(,)a x y x y λλλλ==。
四、两平面向量平行和垂直的充要条件1、平行(共线):基本定理:a 、b 互相平行的充要条件是存在一个实数λ,使得a b λ=。
定理:已知11(,)a x y =,22(,)b x y =,则a ∥b 的充要条件是01221=-y x y x .2、垂直:基本定理:a 、b 互相垂直的充要条件是0a b ⋅=。
定理:已知11(,)a x y =,22(,)b x y =,则a ⊥b 的充要条件是02121=+y y x x 。






平面向量的加减运算及其几何意义科目:高一数学 主备人:王小红 个体初备时间:2011年5月11 集体备课时间: 备课组长签字: 【学习目的】(1)理解向量加减法的概念及向量加减法的几何意义(2)理解向量的加法交换律和结合律,并能熟练地运用它们进行向量计算。
【学习重点】向量加法运算(三角形法则,平行四边形法则),向量的减法运算及其几何意义。
【学习难点】对向量加法法则和减法的定义的理解,特别是向量减法定义的理解。
【学习过程】引入:以前台胞春节期间来大陆探亲,乘飞机先从台北到香港,再从香港到上海。
2008年7月4日,两岸直航包机启航 。
若台北到香港的位移用向量a ⃗ 表示,香港到上海的位移用向量b ⃗ 表示,台北到上海的位移用向量c 表示,思考:向量a ⃗ ,b ⃗ ,c 有何关系?探究1.向量加法的三角形法则如图:已知非零向量a ⃗ ,b ⃗ ,在平面内任取一点A ,作AB ⃗⃗⃗⃗⃗ =a ⃗ ,BC ⃗⃗⃗⃗⃗ =b ⃗ ,则向量AC ⃗⃗⃗⃗⃗ 叫做a ⃗ 与b⃗ 的和,记作 ,即a ⃗ +b ⃗ = = . 注意:用三角形法则求两个非零向量的和时, 要求这两个向量即第一个向量的终点是第二个向量的起点。
这两个向量的和是指第一个向量的起点为 起点,以第二个向量的终点为终点的向量。
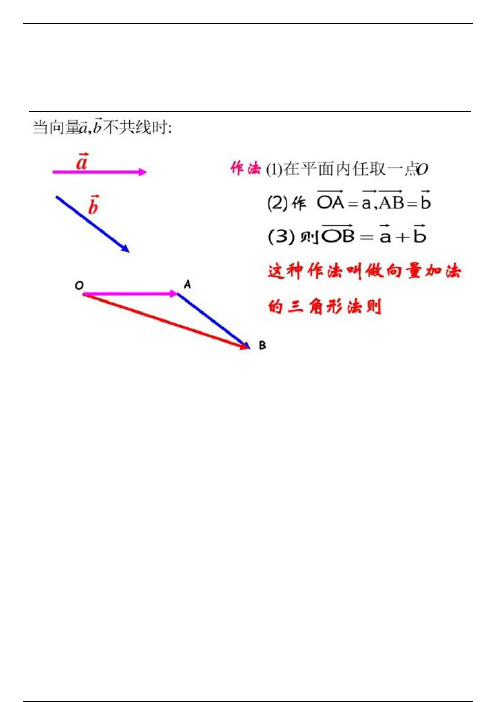
探究2.向量加法的平行四边形法则 如图:已知非零向量a ⃗ ,b ⃗ ,在平面内任取一点0, 作OA ⃗⃗⃗⃗⃗ =a ⃗ ,OB ⃗⃗⃗⃗⃗ =b ⃗ ,以OA,OB 为邻边作平行四边形OACB ,则向量OC ⃗⃗⃗⃗⃗ 就是a ⃗ 与b⃗ 的和, 记作a ⃗ +b ⃗ ,即a ⃗ +b ⃗ = = . 求两个向量和的运算,记作向量的加法 探究3.向量的加法运算律①交换律: . ②结合律: . 画图简单证明:探究4.向量加法的几个重要的结论: (1)对于零向量与任一向量a ⃗ 的和,有 a ⃗ +0⃗ = = .(2)AB ⃗⃗⃗⃗⃗ +BA⃗⃗⃗⃗⃗ = . (3)向量加法的三角形法则可推广到多个向量相加,即AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ +…+PQ⃗⃗⃗⃗⃗ +QR ⃗⃗⃗⃗⃗ = . (4)向量模的不等关系:∣a ⃗ +b ⃗ ∣ ∣a ⃗ ∣+∣b ⃗ ∣,当a ⃗ ,b ⃗ 方向相同时取等号; ∣a ⃗ -b ⃗ ∣ ∣a ⃗ ∣+∣b ⃗ ∣, 当a ⃗ ,b ⃗ 方向相反时取等号。

向量在高一第几章的知识点向量在高一数学课程中属于第二章的内容,主要包括以下知识点:1. 向量的定义与表示向量是有大小和方向的量,通常用箭头AB来表示。
向量可以用有序数对(x, y)来表示,其中x表示水平方向的分量,y表示垂直方向的分量。
2. 向量的相等与运算两个向量相等的条件是它们具有相同大小和相同方向。
向量的加法满足交换律和结合律,即A+B=B+A,(A+B)+C=A+(B+C)。
3. 向量的数量积与向量积数量积,也称点积或内积,是两个向量的乘积与夹角的余弦值的乘积。
向量积,也称叉积或外积,是两个向量的乘积与夹角的正弦值的乘积。
4. 向量的平行与垂直两个向量平行的条件是它们的方向相同或相反。
两个向量垂直的条件是它们的数量积为0。
5. 向量的投影与正交分解向量的投影是指一个向量在另一个向量上的投影长度。
正交分解是将一个向量分解为与另一个向量垂直和平行的两个向量之和。
6. 向量的模与单位向量向量的模是指向量的大小,可以用勾股定理求得。
单位向量是模为1的向量,可以通过将向量除以其模得到。
7. 向量的线性组合与线性相关性向量的线性组合是指将多个向量与常数相乘后相加所得到的新向量。
如果存在一组非零向量的线性组合等于零向量,则这组向量线性相关。
8. 向量的夹角与方向余弦两个向量的夹角可以通过它们的数量积和模的关系求得。
方向余弦是夹角余弦的正负值。
9. 平面向量的坐标运算对于平面内的向量,可以通过坐标运算进行计算。
比如向量的加减法、数量积和向量积等。
以上是高一数学课程中向量的主要知识点,通过学习这些内容,可以掌握向量的基本概念、运算规则和应用技巧。
[教材优化全析]
1.向量的加法 (1)引入
①某人从A 到B ,再从B 按原方向到C ,则两次的位移和:
+BC =AC . A B C
②若上题改为从A 到B ,再从B 按反方向到C ,则两次的位移和:AB +BC =AC .
③某车从A 到B ,再从B 改变方向到C ,则两次的位移和:
AC +BC =AC . A B
C
上述①②③三个小题,说明向量共线、不共线时都可依据向量的运算法则
求“和”.
(2)向量的加法的定义 已知向量a 、b ,在平面内任取一点A ,作=a ,=b ,则向量叫
做向量a 、b 的和.记作a +b ,即a +b =+BC =AC .
求两个向量和的运算,叫做向量的加法.
对于零向量与任意向量a ,有a +0=0+a =a .
(3)两个向量的和向量的作法
如图(1)、(2)、(3)中,=a ,BC =b ,则+BC =AC
.
(1)
(2)
(3)
A C
①三角形法则:上面的(1)、(2)、(3)中各有两个向量,把其中一个向量的起点平移,使之与第二个向量的终点重合,则第一个向量的起点指向第二个向量终点的向量,就是两个向量的和向量.常说两个向量“首尾相接”. 1°三角形法则对于两个向量共线时也适用. 2°可将向量加法的三角形法则推广到多个向量相加的多边形法则. 3°任何一个向量均可以写成两个任意向量之和,只要注意到这个向量的全析提示
向量运算是运用向量方法解决问题的基本工具,而向量的加法运算是最基本的向量运算之一,向量加法
的平行四边形法则与三角形法则和物理中力的合成、速度的合成完全一
致.
思维拓展
两个向量的和仍是一个向量,这
如同两个力的合力仍是力(向量)一样.
全析提示
向量有几何表示法和字母表示法两种情况.用几何法表示时,箭头所指的方向是正方向;用字母表示时,起点字母在前,终点字母在后,方向由起点指向终点.
思维拓展 向量是既有大小又有方向的量,
向量的模与方向可通过解三角形的知识求得;对于首尾相连的几个向量的和,等于以第一个向量的起点为起
点,第n 个向量的终点为终点的向量.
起点、终点即可,如:=+,如下所示,O点具有任意性.
A
B O
课本99页例1.求a+b,在平面内任取一点O,平移a、b使之首尾相接,求和向量.实际上我们常在其中a或b上取一点,只平移一个向量即可.如可把a 的起点移至b的终点可求和向量.
②平行四边形法则
由同一点A为起点的两个已知向量a、b为邻边作平行四边形ABCD,则以A为起点的对角线就是a与b的和.这种作两个向量和的方法叫做平行四边形法则.
不能.因为不可能以两平行向量为邻边作平行四边形.所以,平行四边形法则对于两个向量共线时不适用.
(3)两向量的和向量与原向量之间的关系(方向与模).
①当向量a、b不共线时,a+b的方向与a、b不同向,且|a+b|<|a|+|b|.②当向量a、b同向时,a+b的方向与a、b同向,且|a+b|=|a|+|b|.
当向量a、b反向时,若|a|>|b|,则a+b的方向与a同向,且|a+b|=|a|-|b|.若|a|<|b|,则a+b的方向与a反向,且|a+b|=|b|-|a|.
(4)向量的运算律
①交换律:a+b=b+a.
证明:当向量a、b不共线时如下图,作平行四边形ABCD,使=a,=b
,
则BC=b,DC=a.
全析提示
不管平面内的点O选在何处,对于首尾相连的两个和向量,它的方向总是由第一向量的起点指向第二向量的终点.
要点提炼
在几何中向量的加法是用几何作图来定义的.它有两种法则,其中三角形法则比平行四边形法则更具有一般性.像两个向量共线时就只能用三角形法则了.
全析提示
当向量a、b不共线时,|a|、|b|及|a+b|构成一个三角形的三条边,由三角形的性质可知:||a|-|b||<|a+b|<|a|+|b|;当向量a、b共线时,|a|、|b|及|a+b|可理解成同一直线上的线段相加减.
要点提炼
向量的加法同实数的加法一样,满足交换律与结合律.
因为=+=a+b,=+=b+a,
所以a+b=b+a.
当向量a、b共线时,若a与b同向,由向量加法的定义知:
a+b与a同向,且|a+b|=|a|+|b|,
b+a与a同向,且|b+a|=|b|+|a|,
所以a+b=b+a;
若a与b反向,不妨设|a|>|b|,同样由向量加法的定义知:
a+b与a同向,且|a+b|=|a|-|b|,
b+a与a同向,且|b+a|=|a|-|b|,
所以a+b=b+a.
综上所述,a+b=b+a.
②结合律,自己验证一下.由于向量的加法满足交换律和结合律,对于多个向量的加法运算就可以按照任意的次序与任意的组合来进行了.
例如化简:(+)+=(+)+=+=.
又如化简:CM+(BC+)=(CM+)+BC=CB+BC=0,也
可写成CM+(MB+BC)=CM+MC=0.
2.向量的减法
(1)相反向量:与a长度相等、方向相反的向量叫做相反向量,
记作:-a.
①规定:零向量的相反向量仍是零向量.
②a与-a互为相反向量,即-(-a)=a.
③任意向量与它的相反向量的和是零向量,即a+(-a)=(-a)+a=0.
又如:与互为相反向量,+=0.
④如果a、b互为相反向量,那么a=-b,b=-a,a+b=0.
(2)向量减法的定义
向量a加上b的相反向量,叫做a与b的差,
即a-b=a+(-b).
求两个向量的差的运算叫做向量的减法,向量的减法是向量加法的逆运算.若b+x=a,
则x叫做a与b的差,记作a-b.
(3)a-b的作法
由(a-b)+b=a+(-b)+b=a+0=a.
所以a-b就是这样一个向量,它与b的和等于a.
①已知a、b,怎样求作a-b?
解法一:已知向量a、b,在平面内任取一点O,作=a,=b,则=a -b,即a-b可以表示为从向量b的终点指向向量a的终点的向量.
思维拓展
当向量a与b共线时,求a与b 的和,不管是b以a的终点为起点,还是a以b的终点为起点,它们的和都是从第一个向量的起点指向第二个向量的终点,从图象上看都是相等的.
要点提炼
由于向量可用表示它的有向线段的起点和终点的字母来表示,根据向量加法的三角形法则,可把首尾相连的向量先结合在一起相加.
全析提示
向量的减法与加法互为逆运算,有关向量的减法可同加法相类比,也可同实数的减法相类比.
全析提示
两个向量的差同两个向量的和一样,其运算结果仍是一个向量,它的模与方向可通过解三角形知识求得.
全析提示
由于向量是以OB的终点为起点的向量,所以根据向量加法的三角形法则有=+,即a+(a
A
解法二:在平面内任取一点O ,作=a ,=b ,则=a -b , 即a -b 也可以表示为从向量a 的起点指向向量b 的起点的向量
.
解法三:在平面内任取一点O ,作OA =a ,OB =-b ,则由向量加法的平行四边形法则可得 OC =a +(-b )=a -b .
②如下图,若a 与b 共线时,怎样作a -b ?
(1)
(2)
在平面内任取一点O
,作=a ,=b .
则为所求的向量a -b .
(1)
(2)
B
一般地,不论两向量共线还是不共线,常选取一个适当的点,通过平移把两向量的起点重合,则由减数向量的终点指向被减数向量的终点的向量,即为所求的差向量.
平行四边形ABCD 中,若设=a ,=b ,
则两条对角线都可以用a 与b 表示,借助这一模型可进一步研究有关ABCD
的一些性质.如课本103页例4.AC =a +b ,DB =a -b .
变式训练一:当a 、b b 垂直?
-b )=b .显然减法是加法的逆运算.
思维拓展
向量a -b =a +(-b ),即向量的减法可用向量加法的三角形法则或平行四边形法则来表示,是化生为熟,化未知为已知的化归思想的具体应用.
要点提炼
若向量a 、b 是共线向量,则a ±b 与a 、b 仍是共线向量.
全析提示
从同一点出发的两个不共线向量的和、差同两个向量一起恰好构成一个平行四边形的边与对角线.
变式训练二:当a、b满足什么条件时,|a+b|=|a-b|?
变式训练三:a+b与a-b可能是相等向量吗?
变式训练四:当a与b满足什么条件时,a+b平分a与b所夹的角?
答案:一、|a|=|b|,
即ABCD为菱形,对角线互相垂直.
二、|a+b|=|a-b|,即ABCD 的对角线长相等,ABCD应为矩形,所
以应满足a与b垂直.
三、a+b与a-b 不可能相等,因为ABCD的方向不同.
四、当|a|=|b|时,对角线平分a与b所夹的角.
全析提示
以平行四边形为起点,借助平面
几何图形的性质解答上述问题.。